Как доказать что правильный четырехугольник квадрат

Радиус вписанной окружности для квадрата равен половине его стороны (Формула 1)

Длина диагонали равна корню квадратному из двух, умноженному на длину стороны (Формула 2)

Радиус описанной окружности равен половине диагонали и равен стороне квадрата, умноженной на корень из двух на два (Формула 3)

Периметр квадрата равен стороне умноженной на четыре или четырем корням из двух, умноженных на радиус описанной окружности или восьми радиусам вписанной окружности (Формула 4)

Площадь квадрата равна квадрату сторон или двум квадратам радиусов описанной окружности или четырем квадратам радиуса вписанной в него окружности (Формула 5)

Радіус вписаного кола для квадрата дорівнює половині його сторони (Формула 1)

Довжина діагоналі дорівнює Корню квадратному з двох, помноженому на довжину сторони (Формула 2)

Радіус описаного кола дорівнює половині діагоналі і дорівнює стороні квадрата, помноженій на корінь з двох на два (Формула 3)

Периметр квадрата дорівнює стороні помноженоi на чотири або чотирьом корням з двох, помножених на радіус описаного кола або восьми радіусам вписаного кола (Формула 4)

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Какой четырехугольник называется квадратом, а какой прямоугольником. Какой четырехугольник называется трапецией

Четырехугольники, как частный случай многоугольников, очень важная тема, изучаемая в школьном курсе геометрии. Современная программа подразумевает ознакомление с этим материалом в восьмом классе. В рамках школьного обучения рассматриваются исключительно выпуклые четырехугольники. Остальные же изучаются на уровне высших учебных заведений.

Изучение четырехугольников происходит в разных программах изучения геометрии неодинаково. Порядок введения понятия зависит от последовательности подачи материала о многоугольниках.

Видео:№1080. Докажите, что любой правильный четырехугольник является квадратом.Скачать

Порядок изучения четырехугольников

Вам будет интересно: Формула решения квадратных уравнений и примеры ее использования

В одном случае четырехугольник рассматривается как частный случай многоугольника, в другом — определяется как совокупность отрезков и точек, расположенных на их пересечении, числом по четыре. При этом должны выполняться условия непринадлежности любых из трех этих точек одной прямой, и отсутствия пересечений, кроме как в вершинах.

В большинстве школ Четырехугольники изучаются в восьмом классе. Изучив сначала параллельность прямых, затем теорему о сумме углов многоугольника, переходят к параллелограмму. Рассмотрев его признаки и доказав связанные с ними теоремы, переходят к остальным частным случаям, получая ответы на вопросы: какой четырехугольник называется квадратом, ромбом, прямоугольником и различными видами трапеций.

Вам будет интересно: Какова площадь земного шара?

Еще один подход — изучение четырехугольников при рассмотрении темы подобных фигур. Здесь также последовательно изучаются четырехугольники начиная с параллелограмма. Определяется – какой четырехугольник называется прямоугольником, трапецией. И конечно, подробно рассматривается, какими фигурами могут быть остальные четырехугольники.

Видео:Как построить квадрат, два способаСкачать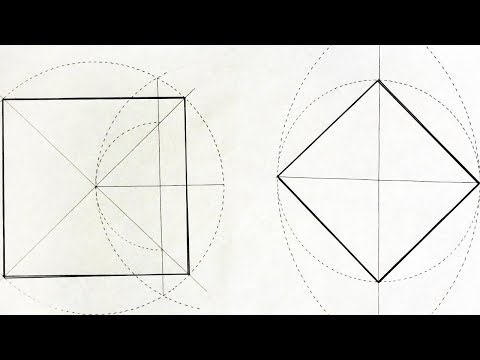

Классификация фигур с четырьмя углами

Какой четырехугольник называется квадратом? Выяснить это можно, изучив все фигуры, имеющие отношения к данной по порядку. Первым в наше внимание попадет объект, называемый параллелограммом. Он образуется четырьмя прямыми попарно параллельными и пересекающимися. Отдельно определяются случаи, когда это происходит под углами в девяносто градусов и те, в которых все отрезки, образованные таким пересечениями, имеют одну длину. В завершение, выясним, какой четырехугольник называется трапецией.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Четырехугольники, называемые выпуклыми

Остановимся на понятиях выпуклых, а также невыпуклых четырехугольников. Данное различие имеет большое значение, так как в школьной программе изучаются только первые из них.

Какой четырехугольник называется выпуклым? Для того чтобы разобраться в этом последовательно, проведем через все стороны фигуры прямые линии. Если во всех случаях весь четырехугольник лежит в одной из двух полуплоскостей образованных этой прямой – он выпуклый. В противном случае, соответственно, невыпуклый.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Обычный параллелограмм

Теперь рассмотрим основные виды выпуклых четырехугольников. Начнем с параллелограмма. Выше мы приводили определение этой фигуры. Кроме определения стоит отметить несколько свойств этого выпуклого многоугольника.

Стороны параллелограмма, находящиеся напротив друг друга равны. Также равны друг другу и противоположные углы.

Пересечение отрезков, называемых диагоналями, образует угол в девяносто градусов. Если просуммировать квадраты их длин, то они составят сумму квадратов граней фигуры. Каждый такой отрезок образует два одинаковых треугольника и четыре равновеликих.

Любые два соседних угла при сложении дадут сто восемьдесят градусов.

При констатации факта, что геометрическая фигура обладает данными свойствами, можно утверждать, что она — параллелограмм. Таким образом, мы получим признаки этого четырехугольника, определяющие принадлежность фигуры именно к этому классу.

Площадь можно найти двумя способами. Первым будет являться поиск произведения синуса угла и длин, прилежащих к нему сторон. Второй способ — определение результата перемножения длин высоты и лежащей напротив нее грани.

Какой четырехугольник называется ромбом? Такой, у которого все из образовывающих его сторон равняются между собой. Эта геометрическая фигура обладает всеми свойствами и признаками параллелограмма. Еще одним свойством является факт, что в эту фигуру всегда вписывается окружность.

Параллелограмм, соседние стороны которого равны, однозначно определяется, как ромб. Площадь можно вычислить, как произведение квадрата стороны на синус одного из углов.

Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Прямоугольник

Какой четырехугольник называется прямоугольником? Такой, который обладает углами в девяносто градусов. Так как он тоже является параллелограммом, на него распространяются свойства и признаки этого четырехугольника. Также о прямоугольнике можно сказать следующее:

• Диагонали этой фигуры имеют одинаковую длину.
• Площадь определяется путем умножения сторон друг на друга.
• В случае, когда угол параллелограмма составляет девяносто градусов – можно утверждать, что это прямоугольник.

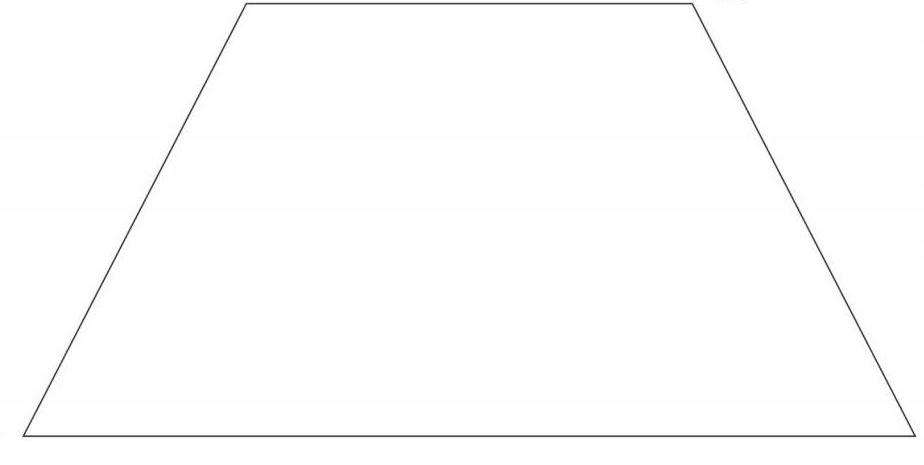
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Квадрат

Следующий вопрос из тех, что мы рассмотрим в этой публикации, – какой четырехугольник называется квадратом? Это фигура, обладающая равными сторонами и углами в девяносто градусов. Исходя из указанных выше параметров, она обладает всеми теми же свойствами, которыми обладают прямоугольник и ромб. Соответственно имеет также их признаки.

К особенностям квадрата можно отнести уникальные свойства линий, соединяющих его противоположные вершины и называемых диагоналями. Они имеют одну длину и пересекаются под прямым углом.

Прикладное значение квадрата сложно переоценить. Благодаря своей универсальности, простоте определения площади и размеров, эта фигура широко используется в качестве эталонной меры. Число возведенное во вторую степень устойчиво называется математиками квадратом. С помощью квадратных единиц измеряют площадь, осуществляют интеграцию и общие приближения размеров на плоскости. Широко эта геометрическая концепция используется в архитектуре и ландшафтном дизайне.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Трапеция

Далее следует рассмотреть какой четырехугольник называется трапецией. Это будет фигура, имеющая расположенные параллельно друг другу стороны, называемые основаниями и непараллельные стороны, определяемые боковыми. Она образована четырьмя гранями и таким же количеством углов. Когда эти непараллельные отрезки равны, трапецию определяют как равнобокую. В случае, если у фигуры угол равен девяносто градусов, она будет считаться прямоугольной.

Такой четырехугольник, какой называется трапецией имеет еще один особый элемент. Линию, которая соединяет центры боковых сторон, называют средней. Длину ее можно определить, отыскав одну вторую результата сложения длин сторон, определяемых, как основания фигуры.

У равнобедренной трапеции так же, как и у равнобедренного треугольника, длины диагонали и углы между боковыми сторонами и основаниям равны.

Вокруг такой трапеции всегда возможно описание окружности.

Вписывается окружность в такую фигуру, сумма длин боковых сторон которой одинакова с результатом сложения ее оснований.

Видео:Построение правильного квадрата.Скачать

Общие выводы по теме

В заключение можно сказать что в курсе геометрии достаточно доступно и подробно рассмотрен вопрос о том, какой четырехугольник называется квадратом. Несмотря на то, что в разных учебниках мы можем встретить некоторые отличия в последовательности изложения обозначенных выше тем, все они исчерпывающе освещают тему четырехугольников.

Видео:8 класс, 8 урок, Ромб и квадратСкачать

Четырехугольник

Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Видео:Прямоугольник. 8 класс.Скачать

Виды четырехугольников

Четырехугольники бывают следующих видов:

• Параллелограмм − четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1).
• Трапеция − четырехугольник, у которого две противоположные стороны параллельны (Рис.2).
• Прямоугольник − четырехугольник, у которого все углы прямые (Рис.3).
• Ромб − четырехугольник, у которого все стороны равны (Рис.4).
• Квадрат − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
• Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
• Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).

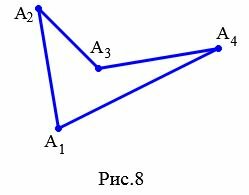
Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Обозначение четырехугольника

Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют ( small A_1A_2A_3A_4 ) или ( small A_4A_3A_2A_1 ) (Рис.8).

Видео:Параллелограмм. Свойства. Прямоугольник, ромб, квадрат. ЗАДАЧИСкачать

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины ( small A_2 ) и ( small A_3 ) являются соседними, так как они являются концами стороны ( small A_2A_3. )

Видео:Задача, которую боятсяСкачать

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны ( small A_2A_3 ) и ( small A_3A_4 ) являются смежными, так как они имеют общую вершину ( small A_3. )

Видео:23-04 геом 9 правильный четырехугольникСкачать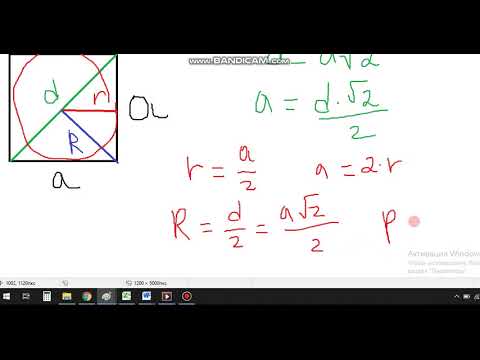

Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

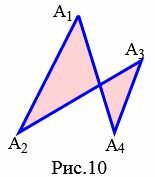
На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны ( small A_1A_4 ) и ( small A_2A_3 ) пересекаются. Такой четырехугольник называется самопересекающийся.

Видео:11 класс, 44 урок, Описанный четырехугольникСкачать

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

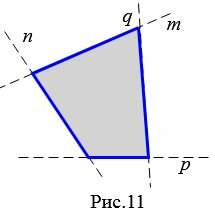
На рисунке 11 четырехугольник лежит по одну сторону от прямых ( small m, n, p, q, ) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

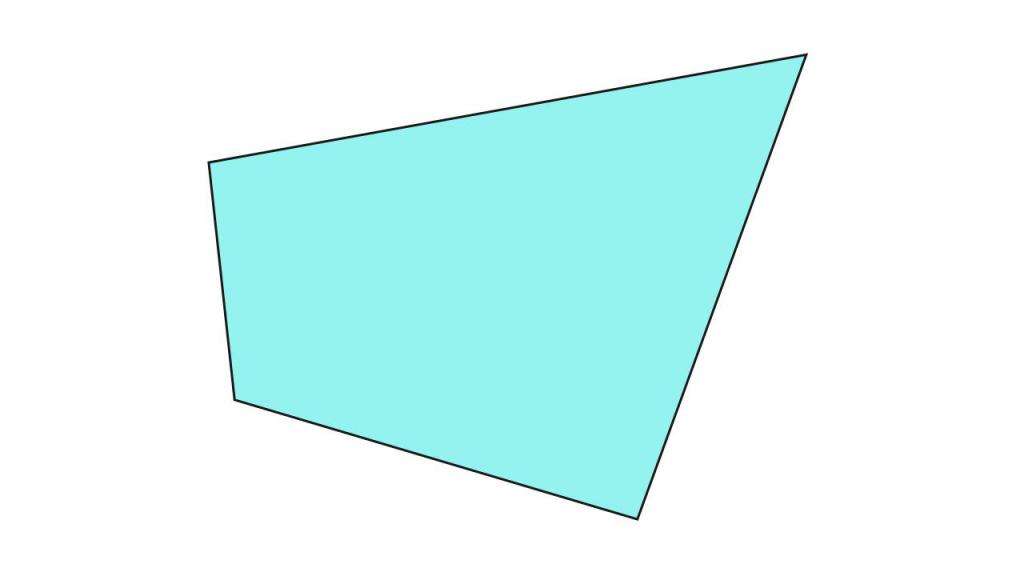
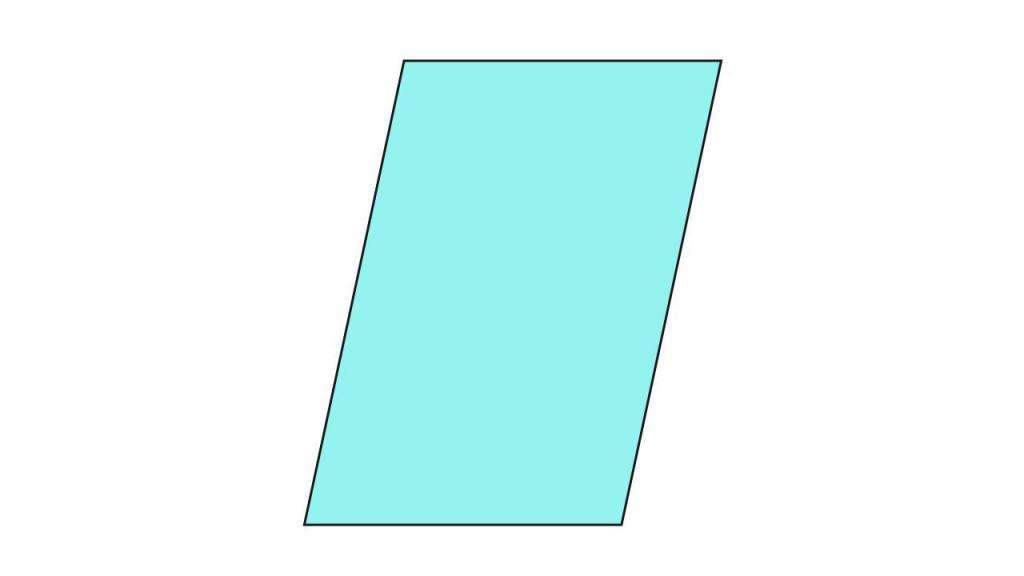
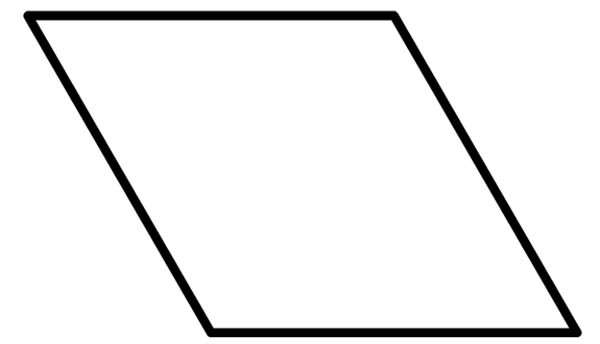
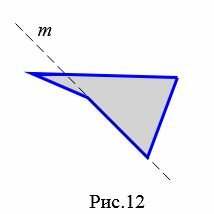
На рисунке 12 прямая ( small m) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой ( small m). Следовательно, этот четырехугольник не является выпуклым.

Видео:8 класс, 7 урок, ПрямоугольникСкачать

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Видео:Хитрый периметрСкачать

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника ( small A_1A_2A_3A_4 ) периметр вычисляется из формулы:

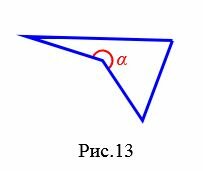
Угол четырехугольника

Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол ( small alpha ) на рисунке 13).

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

На рисунке 14 угол α является внутренним углом четырехугольника при вершине ( small A_4, ) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Сумма внешних углов четырехугольника

Пусть задан четырехугольник ( small A_1A_2A_3A_4 .) Внешний угол при вершине ( small A_1) равен ( small 180°-angle A_1.) Аналогично, внешние углы при вершинах ( small A_2, A_3, A_4 ) равны ( small 180°-angle A_2, ) ( small 180°-angle A_3, ) ( small 180°-angle A_4, ) соответственно. Тогда сумма внешних углов четырехугольника равна:

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB