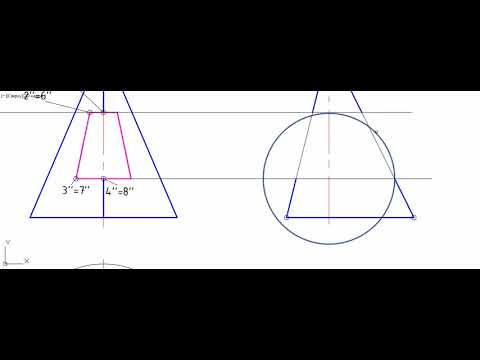
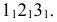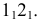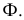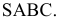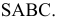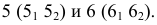Построение проекции правильной четырехугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой четырехугольник без искажения (рисунок 171, а). Фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки S’ (вершины, пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию S» вершины. Соединяя точку S» с точками Г‘, 2″, 3″ и 4″, получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки S’ с горизонтальными проекциями точек Г, 2‘, 3′ и 4′.
Пусть, например, дана фронтальная проекция А» точки А, расположенной на грани пирамиды 1″, S», 2″ и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через А» вспомогательную прямую, проходящую через вершину пирамиды и точку N«,
расположенную на ее грани. Горизонтальную проекцию N’S’ вспомогательной прямой находят, применяя линию связи. Искомая горизонтальная проекция А’ точки А находится на пересечении линии связи, проведенной из точки А» с горизонтальной проекцией N’S’ вспомогательной прямой.
Изометрическая проекция пирамиды выполняется следующим образом (рисунок 171, б).
Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — длину диагонали 24. Из точки О пересечения диагоналей проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Изометрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От начала координат О по оси х откладывают координату хА, из ее конца параллельно оси у — координату уА и из конца этой координаты параллельно оси z — третью координату zA. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату хв и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.
- Проекции пирамиды с основанием четырехугольник
- Многогранники в начертательной геометрии с примерами
- Многогранники
- Точка и прямая на поверхности многогранника
- Способ граней
- Способ ребер
- Развертки многогранников
- Примеры решения задач
- Что такое многогранник
- Пересечение многогранников плоскостями
- Пересечение прямой с многогранником
- Взаимное пересечение многогранников
- Развертки многогранников
- Пересечение пирамиды проецирующими плоскостями
- Пересечение призмы проецирующими плоскостями
- Многогранники и тела с кривыми поверхностями
- Пересечение многогранника плоскостью
- Пересечение конуса и цилиндра плоскостью
- Пересечение прямой линии с поверхностью многогранника
- Пересечение прямой линии с поверхностью конуса и цилиндра
- Построение разверток поверхностей
- Развертка поверхности пирамиды
- Развертка поверхности призмы
- Развертка поверхности конуса
- Развертка поверхности цилиндра
- Взаимное пересечение геометрических тел
- Взаимное пересечение поверхностей многогранников
- Пересечение поверхности вращения и поверхности многогранника
- Взаимное пересечение поверхностей вращения
- Способы задании многогранников и построение их проекций
- Пересечение плоскости и прямой с многогранниками
- Взаимное пересечение многогранников
- 📹 Видео
Видео:Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Проекции пирамиды с основанием четырехугольник
14.1. Определение пирамиды и её элементов
Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).
Многоугольник называется основанием пирамиды, остальные грани — боковыми гранями пирамиды, их общая вершина — вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами её основания, называются боковыми рёбрами пирамиды .
Пирамиду с основанием АВСDЕ и вершиной Р обозначают PABCDE .
Перпендикуляр, опущенный из вершины пирамиды на плоскость её основания, называется высотой пирамиды . Длину этого перпендикуляра также называют высотой пирамиды.
Пирамида называется n-угольной, если её основанием является n-угольник .
На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.
У n- угольной пирамиды имеется ( n + 1) вершин, 2 n рёбер и ( n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.
Треугольную пирамиду (рис. 97) называют также тетраэдром ( « тетраэдр» по-гречески означает «четырёхгранник» ) . Тетраэдр — это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.
14.2. Некоторые виды пирамид
Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то : а ) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды ; б ) все боковые рёбра пирамиды равны между собой.
Доказательств о. а) Пусть отрезок РО — высота пирамиды PABCDEF, все рёбра которой составляют с плоскостью основания угол ϕ (рис. 98). Тогда прямоугольные треугольники РОА, POB, POC, POD, РОЕ и POF, имея общий катет РО, равны между собой (по катету и острому углу ϕ ) . Из равенства этих треугольников следует: ОА = OВ = ОС = OD = OE = OF, т. е. вершины основания пирамиды равноудалены от основания О её высоты РО. Это означает, что точка О — центр окружности, описанной около основания ABCDEF данной пирамиды.
б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼
Вы самостоятельно можете доказать обратные утверждения.
1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.
2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.
Также имеет место следующее утверждение.
Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.
Доказательств о. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).
Проведём высоты РН 1 , РH 2 , РН 3 , PH 4 , РH 5 боковых граней.
Тогда по теореме о трёх перпендикулярах получаем OH 1 ⟂ AB, OH 2 ⟂ BC, OH 3 ⟂ CD, OH 4 ⟂ DE, OH 5 ⟂ EA, следовательно, ∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = ∠ OH 4 P = ∠ OH 5 P = ϕ . Поэтому △ OH 1 P = △ OH 2 P = △ OH 3 P = △ OH 4 P = △ OH 5 P (как прямоугольные с общим катетом OP и острым углом ϕ ) . Из равенства этих треугольников следует ОН 1 = OH 2 = OH 3 = ОН 4 = ОН 5 , т. е. точка О — основание высоты РО пирамиды — равноудалена от всех сторон многоугольника ABCDE. Это означает, что точка O является центром окружности, вписанной в основание ABCDE данной пирамиды. Теорема доказана. ▼
Самостоятельно докажите обратное утверждение.
Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
Перечислим ещё несколько часто встречающихся в задачах видов пирамид.
• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).
• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).
• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).
14.3. Правильная пирамида
Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.
Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.
Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.
На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.
Правильные пирамиды обладают замечательным свойством.
В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.
Доказательств о. Рассмотрим правильную n- угольную пирамиду РА 1 А 2 . A n . Пусть точка O — центр n- угольника A 1 A 2 A 3 . A n ; отрезок РО — перпендикуляр к плоскости основания пирамиды (рис. 104).
Так как центр правильного многоугольника является центром окружности, описанной около этого многоугольника, то ОА 1 = OA 2 = OA 3 = . = OA n (как радиусы описанной окружности). Тогда равны боковые рёбра пирамиды, как наклонные к плоскости её основания, имеющие равные проекции, т. е. PA 1 = PA 2 = PA 3 = . = PA n .
Таким образом, имеем:
РА 1 = РA 2 = . = PA n (как боковые рёбра);
A 1 A 2 = A 2 A 3 = . = A n A 1 (как стороны правильного n- угольника).
Следовательно, треугольники PA 1 A 2 , РA 2 A 3 , . PA n A 1 являются равнобедренными и по третьему признаку равенства треугольников равны между собой.
Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.
Так как точка О — центр правильного n- угольника A 1 A 2 A 3 . A n , лежащего в основании правильной пирамиды PA 1 A 2 . A n , РО — перпендикуляр к плоскости её основания, то при вращении данной пирамиды вокруг оси ОР на угол, равный 
Следствием доказанного выше является утверждение.
Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.
Докажите это предложение самостоятельно.
Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.
Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.
Имеют место признаки правильной пирамиды:
Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.
Докажите это самостоятельно.
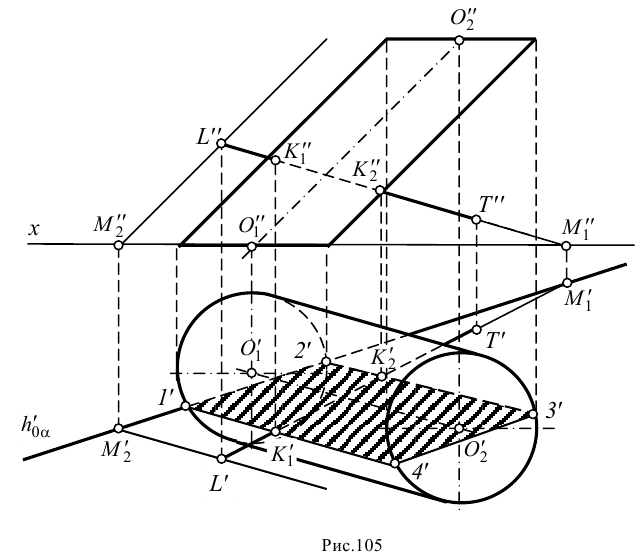
ЗАДАЧА (2.245). Высота правильной четырёхугольной пирамиды равна h и образует с боковой гранью угол α . Через сторону основания пирамиды проведена плоскость, перпендикулярная противоположной грани и пересекающая её. Найти площадь сечения.
Дан о: PABCD — правильная пирамида (рис. 105); РО — высота пирамиды, РО = h ; ∠ OPF = α .
Решени е. Первый спосо б . Пусть отрезок EF — средняя линия основания пирамиды. Тогда AD ⟂ EF, AD ⟂ PF ⇒ АD ⟂ ( РEF ) ⇒ ( PEF ) ⟂ ( ADP ) (по признаку перпендикулярности двух плоскостей). Поэтому прямая PF является ортогональной проекцией прямой РO на плоскость ADP. Значит, ∠ OPF — угол между высотой PO и боковой гранью ADP пирамиды: ∠ OPF = α .
Далее имеем: AD ⟂ ( PEF ), ВС || AD ⇒ ВC ⟂ ( PEF ) ⇒ прямая ВС перпендикулярна любой прямой плоскости PEF. Поэтому если FL ⟂ РЕ (в плоскости PEF ) , то BС ⟂ FL. Тогда FL ⟂ ВС, FL ⟂ PE ⇒ FL ⟂ ( BCP ) ⇒ ( ADL ) ⟂ ( ВCР ) (по признаку перпендикулярности двух плоскостей); при этом ( ADL ) ∩ ( ВСР ) = МK , МK || AD, так как плоскости ВСР и АDL проходят через параллельные прямые ВС и AD. Значит, сечение ADKM — трапеция, у которой FL — высота (почему?), откуда
S сеч = 
Найдём AD, МK и FL.
В △ OPF ( ∠ POF = 90 ° ):
OF = OP • tg α = h • tg α ; PF = 

EF = 2 FO = 2 h • tg α = ВС.
В плоскости PEF получаем:
FL ⟂ РЕ, РО ⟂ EF ⇒ ∠ EFL = ∠ OPE = α .
Тогда в △ ЕFL : FL = ЕF • cos α = 2 h • tg α • cos α = 2 h sin α ;
в △ PLF ( ∠ PLF = 90 ° , ∠ PFL = 90 ° – 2 α ):
PL = PF • sin (90 ° – 2 α ) = PF • cos 2 α = 
Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда




= 2 h tg α • cos 2 α .
AD = EF = 2 h • tg α , FL = 2 h • sin α , MK = 2 h • tg α • cos 2 α .
S сеч = 

= 
Замечание. Отрезок MK можно найти следующим образом. Сечением данной пирамиды плоскостью, проходящей через прямую MK параллельно основанию пирамиды, является квадрат MKD 1 A 1 (см. рис. 105). F 1 = A 1 D 1 ∩ PF. У этого квадрата LF 1 = MK. Найдём F 1 L .
В треугольнике LFF 1 имеем ∠ FLF 1 = α ( LF 1 || EF ) ,
∠ F 1 FL = ∠ OFP – ∠ OFL = (90 ° – α ) – α = 90 ° – 2 α ;
∠ FF 1 L = 180 ° – ∠ OFF 1 = 90 ° + α . Тогда по теореме синусов


⇒ LF 1 = 

Значит, MK = LF 1 = 2 h • tg α • cos 2 α .
Второй спосо б . Пусть точки M 1 , K 1 , L 1 — ортогональные проекции на плоскость основания соответственно точек М, K, L (рис. 105, 106). Так как плоскости АСР, BDP и EFP перпендикулярны плоскости основания пирамиды, то ортогональными проекциями прямых PC, РВ и РЕ на эту плоскость являются соответственно прямые АС, BD и EF. Следовательно, M 1 ∈ BD, K 1 ∈ AC, L 1 ∈ EF, причём четырёхугольник ADK 1 M 1 — равнобедренная трапеция.
Таким образом, трапеция ADK 1 M 1 — ортогональная проекция сечения ADKM. Это означает, что S ADKM = 





S ADKM = 

Ответ: 4 h 2 • sin 2 α • cos α .
1 4.4. Площади боковой и полной поверхностей пирамиды
Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.
Площадью боковой поверхности пирамиды (обозначают S бок ) называется сумма площадей всех её боковых граней: S бок = S 1 + S 2 + . + S n , где S 1 , S 2 , . S n — площади боковых граней пирамиды.
Площадью полной поверхности пирамиды (обозначают S полн ) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.
Из определения следует: S полн = S бок + S осн .
О площади боковой поверхности правильной пирамиды имеет место следующая теорема.
Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.
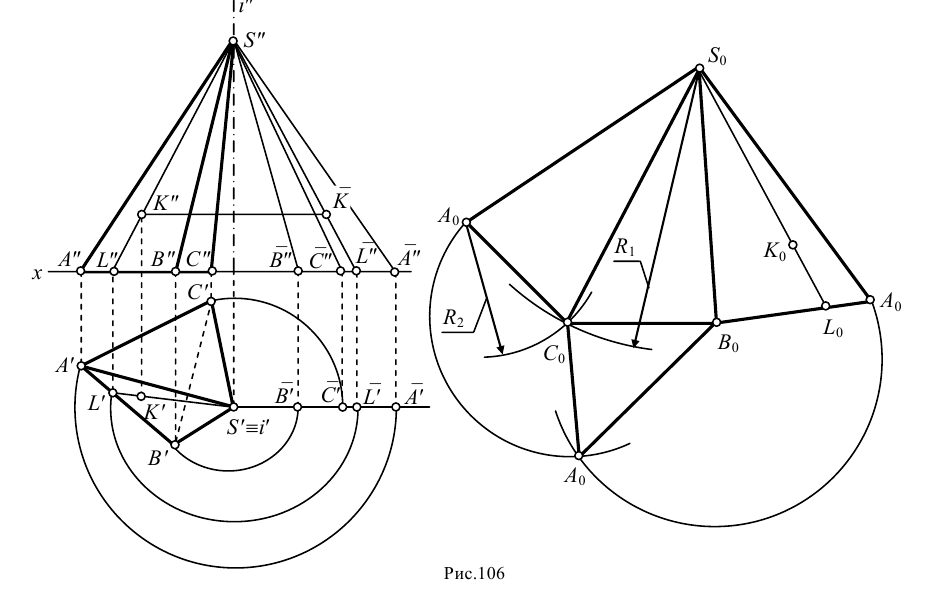
Доказательств о. PA 1 A 2 . A n — правильная пирамида, a — длина её апофемы (рис. 107).
Боковые грани правильной пирамиды — равные равнобедренные треугольники, у которых основаниями являются стороны правильного n- угольника A 1 A 2 . A n , а высоты равны апофеме пирамиды, т. е.
РE 1 = РE 2 = PE 3 = . = PE n = a.
S бок = S △ PA 1 A 2 + S △ PA 2 A 3 + . + S △ PA n A 1 =
= 


= 

где Р — периметр основания пирамиды. Теорема доказана. ▼
Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то S бок = 
Доказательств о. Пусть отрезок PO — высота пирамиды РA 1 A 2 A 3 . A n , все боковые грани которой образуют с плоскостью основания углы, равные ϕ (рис. 108); отрезки PH 1 , PH 2 , . PH n — высоты боковых граней. Тогда (по теореме о трёх перпендикулярах) OH 1 ⟂ A 1 A 2 , OH 2 ⟂ A 2 A 3 , . OH n ⟂ A n A 1 . Значит,
∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = .
. = ∠ OH n P = ϕ .
Так как точка О является центром круга, вписанного в основание пирамиды (почему?), то эта точка лежит внутри n- угольника A 1 A 2 A 3 . A n . Поэтому n- угольник A 1 A 2 . A n является объединением непересекающихся треугольников A 1 OA 2 , A 2 OA 3 , . A n OA 1 . Эти треугольники являются ортогональными проекциями на плоскость основания пирамиды её соответствующих боковых граней. По теореме о площади ортогональной проекции многоугольника имеем:
S △ A 1 OA 2 = S △ A 1 PA 2 • cos ϕ ,
S △ A 2 OA 3 = S △ A 2 PA 3 • cos ϕ ,
.
S △ A n OA 1 = S △ A n PA 1 • cos ϕ .
Сложив почленно эти равенства, получим S осн = S бок • cos ϕ , откуда S бок = 
Так как все боковые грани правильной пирамиды образуют с плоскостью основания равные двугранные углы (пусть величина этих углов равна ϕ , см. рис. 107), то для площади боковой поверхности и площади основания правильной пирамиды также справедлива формула
S бок = 
14 . 5 . Свойства параллельных сечений пирамиды
Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).
Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть сечением пирамиды PABCD плоскостью α , параллельной плоскости β её основания, является четырёхугольник A 1 B 1 C 1 D 1 (см. рис. 109).
Проведём высоту РО данной пирамиды и обозначим O 1 = РО ∩ α .
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 
Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:





где k — коэффициент гомотетии 
Вследствие того, что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии, а k = РO 1 : РО , где РO 1 и РО — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S A 1 B 1 C 1 D 1 : S ABCD = k 2 = 

Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.
14.6. Усечённая пирамида
Плоскость α , параллельная основанию пирамиды PABCD и пересекающая её, делит эту пирамиду на два многогранника: пирамиду РA 1 B 1 C 1 D 1 и многогранник ABCDA 1 B 1 C 1 D 1 (см. рис. 109).
Многогранник ABCDA 1 B 1 C 1 D 1 (рис. 110) называют усечённой пирамидой. Грани ABCD и A 1 B 1 C 1 D 1 , лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усечённой пирамиды , остальные грани — её боковыми гранями . Так как нижнее и верхнее основания усечённой пирамиды гомотетичны (т. 20), то все её боковые грани — трапеции.
Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.
У n- угольной усечённой пирамиды 2 n вершин, 3 n рёбер, ( n + 2) грани и n ( n – 3) диагоналей.
Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О 1 О, B 1 K — высоты усечённой пирамиды.
Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).
Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.
Высоты этих трапеций, соединяющие середины их оснований, называются апофемами усечённой пирамиды . Все её апофемы равны между собой.
Отрезок OO 1 , соединяющий центры оснований правильной усечённой пирамиды, является её высотой .
Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.
Для правильной усечённой пирамиды имеет место
Теорема 21. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему .
Для доказательства теоремы достаточно площадь одной из боковых граней пирамиды умножить на их число. В результате получим формулу S бок = 
Проведите доказательство теоремы самостоятельно.
Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды
S полн = S бок + S 1 + S 2 ,
где S 1 и S 2 — площади большего и меньшего оснований этой пирамиды.
Для усечённой пирамиды, у которой все двугранные углы при рёбрах большего основания равны ϕ , справедливо: S бок = 

14 . 7 . Объём пирамиды
Лемма. Две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики .
Доказательств о. Пусть пирамиды РАВС и P 1 A 1 B 1 C 1 имеют высоты, равные H , и равновеликие основания с площадью S ; их объёмы — соответственно V 1 и V 2 . Докажем, что V 1 = V 2 .
Расположим пирамиды РАВС и P 1 A 1 B 1 C 1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼
Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.
Доказательств о. Пусть А 1 AВC — данная треугольная пирамида с вершиной A 1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA 1 B 1 C 1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA 1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.
Призма АВCA 1 B 1 C 1 является объединением трёх треугольных пирамид с общей вершиной A 1 : A 1 ABC, A 1 BB 1 C 1 и A 1 BCC 1 . Основания BB 1 C 1 и BCC 1 пирамид A 1 BB 1 C 1 и A 1 BCC 1 равны, а высота у них общая. Значит, по лемме эти пирамиды имеют равные объёмы.
Будем считать точку В вершиной пирамиды A 1 BB 1 C 1 , a △ A 1 B 1 C 1 — её основанием. Тогда эта пирамида равновелика пирамиде А 1 AВС, так как у них общая высота, а основания АВС и A 1 B 1 C 1 равновелики (как основания призмы). Таким образом, призма ABCA 1 B 1 C 1 является объединением трёх равновеликих пирамид, одной из которых является данная пирамида A 1 ABC. Это означает, что объём V пирамиды A 1 АВС составляет одну треть объёма призмы ABCA 1 B 1 C 1 , т. е. V = 
V = 
где Н — длина высоты данной пирамиды. Теорема доказана. ▼
На рисунке 114 изображены треугольная призма ABCDEF и составляющие её три равновеликие треугольные пирамиды ABDF, ABCF и BDEF .
Для вычисления объёма n- угольной пирамиды PA 1 A 2 . A n (рис. 115) разобьём её основание A 1 A 2 . A n диагоналями A 1 A 3 , A 1 A 4 , . A 1 A n – 1 на треугольники с общей вершиной A 1 . Тогда данная пирамида разбивается в объединение пирамид PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n с общей вершиной Р и общей высотой, которая равна высоте данной пирамиды. Основаниями этих пирамид являются треугольники разбиения основания данной пирамиды. Это означает (свойство 2 объёмов), что объём V пирамиды PA 1 A 2 . A n равен сумме объёмов V 1 , V 2 , . V n – 2 треугольных пирамид соответственно PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n .
Пусть длина высоты пирамиды равна Н, площадь её основания — S, а площади треугольников разбиения этого основания равны S 1 , S 2 , . S n – 2 . Это означает, что S 1 + S 2 + . + S n – 2 = S. Тогда получаем:
V = V 1 + V 2 + . + V n – 2 = 

Таким образом, объём любой пирамиды вычисляется по формуле
V = 
где S осн — площадь основания, Н — длина высоты пирамиды.
Итак, доказана теорема.

Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼
14.8. Об объёме тетраэдра
У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения
V = 



где S k и h k ( k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.
Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.
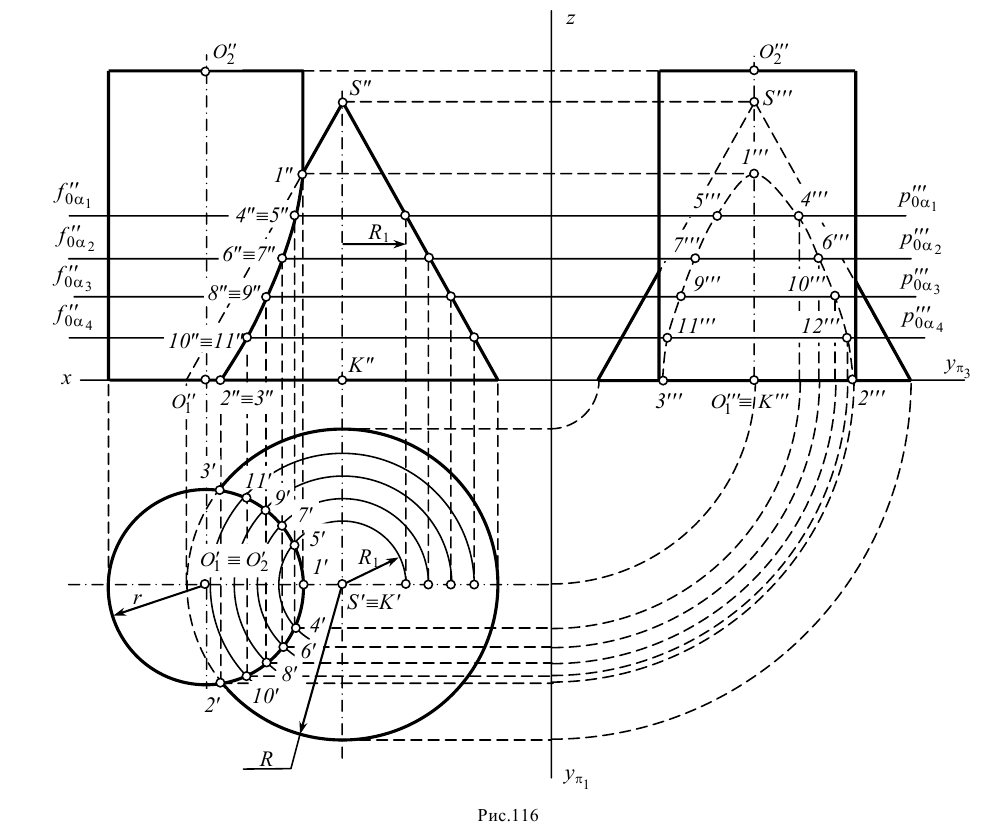
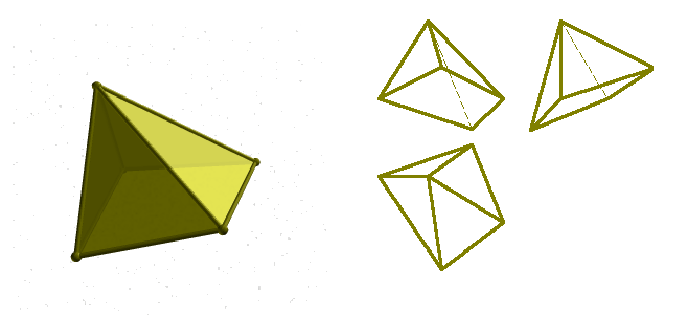
Интересен также тетраэдр (рис. 116, а ), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б ).
Докажите самостоятельно, что в равногранном тетраэдре:
— скрещивающиеся рёбра попарно равны;
— все высоты равны;
— сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180 ° ;
— двугранные углы при скрещивающихся рёбрах тетраэдра равны.
Не менее интересен следующий факт. Пусть дан тетраэдр A 1 C 1 BD . Проведём через каждое его ребро плоскость, параллельную скрещивающемуся с ним ребру. Проведённые шесть плоскостей при пересечении образуют некоторый параллелепипед АВСDA 1 В 1 C 1 D 1 (рис. 117), параллельные грани ABCD и A 1 B 1 C 1 D 1 которого содержат скрещивающиеся рёбра А 1 C 1 и BD данного тетраэдра. Тогда расстояние между основаниями АВСD и А 1 В 1 С 1 D 1 полученного параллелепипеда равно длине его высоты и равно расстоянию между скрещивающимися рёбрами А 1 C 1 и BD данного тетраэдра.
Этот параллелепипед можно разбить на пять тетраэдров — данный тетраэдр A 1 С 1 ВD и ещё четыре тетраэдра: A 1 ABD ; ВВ 1 A 1 C 1 ; C 1 CBD ; DD 1 A 1 C 1 . Объём каждого из четырёх последних тетраэдров равен одной трети высоты h параллелепипеда, умноженной на половину площади его основания ABCD , т. е. шестой части объёма V полученного параллелепипеда.
V A 1 C 1 BD = V – 4 • 




= 
где ϕ — угол между диагоналями АС и BD параллелограмма ABCD . А так как AC || A 1 C 1 , то величина угла между скрещивающимися диагоналями A 1 С 1 и BD тетраэдра А 1 С 1 BD также равна ϕ .
Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.
Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.
1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.
2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.
3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.
Используя рисунок 118, вы сможете легко доказать третье утверждение.
14.9. Объём усечённой пирамиды
Теорема 24. Объём усечённой пирамиды, у которой площади оснований равны S 1 и S 2 , а высота — Н , вычисляется по формуле
V = 

Доказательств о. Пусть дана усечённая пирамида (рис. 119), у которой S 1 > S 2 , а высота OO 1 = H. Дополним эту пирамиду до полной пирамиды с вершиной Р. Объём V данной усечённой пирамиды равен разности объёмов полной и дополнительной пирамид.
Если длина высоты PO 1 дополнительной пирамиды равна x , то высота PO полной пирамиды равна H + x .
Выразим х через S 1 , S 2 и Н. По теореме 20 (o площадях параллельных сечений пирамиды) имеем
S 1 : S 2 = ( H + x ) 2 : x 2 ⇒ 

⇒ x = 
Поэтому для объёма V усечённой пирамиды находим
V = 


= 





= 

Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Многогранники в начертательной геометрии с примерами
Содержание:
Многогранник есть геометрическое тело, ограниченное плоскими многоугольниками — (гранями, пересекающимися по прямым линиям- рёбрам). Фигура сечения многогранника есть плоский многоугольник, сторонами которого являются линии пересечения заданной плоскости с плоскостями граней, а вершинами — точки пересечения рёбер многогранника с заданной плоскостью.
К многогранникам относятся призмы, пирамиды и более сложные объекты.
Призма – это многогранник, основания которого являются n-угольник, а боковые ребра взаимно параллельны.
Пирамида – многогранник, основанием которого является n-угольник, а боковые грани — треугольники.
Построение фигуры сечения многогранника плоскостью может выполняться двумя способами:
- путем определения линии пересечения заданной плоскости с каждой из плоскостей (граней), ограничивающих геометрическое тело многогранника (эти линии — стороны фигуры сечения);
- путем нахождения точек пересечения всех ребер с заданной плоскостью (эти точки — вершины фигуры сечения).
Первый способ называется способом граней, второй — способом ребер. Выбор способа построения фигуры сечения зависит от положения секущей плоскости, рёбер и граней многогранника относительно плоскостей проекций.
Видео:Построение проекций пирамиды. Метод вращения.Скачать
Многогранники
Одним из видов пространственных форм являются многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Эти многоугольники образуют грани, общие стороны многоугольников называются ребрами, вершины многогранных углов, образованных его гранями, сходящихся в одной точке – вершинами многогранника.
Если вершины и ребра многогранника находятся по одну сторону от плоскости любой его грани, то многогранник называется выпуклым. Наибольший практический интерес представляет собой призмы, пирамиды и правильные многогранники (тела Платона).
Многогранник называют правильным, если его грани представляют собой правильные и равные многоугольники. Гранями правильных многоугольников могут быть только правильные треугольники, четырёхугольники (квадраты) и пятиугольники.
Существует пять видов правильных многоугольников:
- Правильный четырёхугольник (тетраэрд) ограничен 4-мя равными правильными треугольниками. Представляет собой правильную пирамиду, в качестве основания которой может быть выбрана любая из 4-х граней;
- Правильный шестиугольник (гекаэдр) ограничен 6-ю равными квадратами – это куб. Представляет собой частный случай правильной призмы;
- Правильный восьмигранник (октаэдр) ограничен 8-ю равносторонними и равными треугольниками .
- Правильный двенадцатигранник (додекаэдр) ограничен 12-ю правильными и равными пятиугольниками;
- Правильный двадцатигранник (икосаэдр) ограничен 20-ю равносторонними и равными треугольниками.
У всякого выпуклого многогранника число граней (Г) плюс число вершин (В) минус число ребер (Р) равно двум, т.е Г + В – Р = 2.
Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона является одновременно стороной другого (но только одного).
Предметом нашего изучения будут только выпуклые многогранники, т.е. такие которые расположены по одну сторону каждой его грани.
Способы задания многогранников. Форма и положение многогранника в пространстве определяется заданием его ребер, основанием и вершиной, если это пирамида, основанием и одним из боковых ребер, если это призма. Построение проекции многогранника сводится к построению проекций точек.
Рассмотрим наиболее распространенные виды многогранников.
Пирамида — это многогранник, одна грань которого многоугольник, а остальные грани — треугольники с общей вершиной (рисунок 6.1).
Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника.
Пирамида называется усеченной, если вершина её отсекается плоскостью. При построении проекций пирамиды целесообразно располагать ее основание параллельно плоскости проекций.
Рисунок 6.1 — Пирамида
Призма — многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы (рисунок 6.2) .
Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом.
При построении проекций призмы целесообразно располагать ее основания параллельно плоскости проекций.
Рисунок 6.2 — Призма
Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники и трапеции, вершины которых являются и вершинами многоугольников оснований (рисунок 6.3).
Рисунок 6.3 — Призматоид
Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
- Тетраэдр — правильный четырехгранник.
- Гексаэдр — правильный шестигранник.
- Октаэдр — правильный восьмигранник.
Точка и прямая на поверхности многогранника
Грани многогранника представляют собой плоскости. Поэтому построение точек и прямых на поверхности многогранника сводится к построению точек и прямых линий на плоскости.
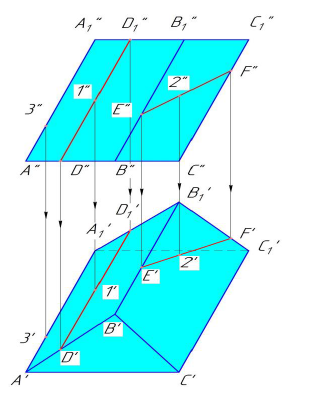
Точки на гранях призмы и пирамиды строятся при помощи вспомогательных прямых, принадлежащих соответствующим плоскостям граней (рисунок 6.4) [5].
Чтобы определить по данной проекции 1» точки 1, лежащей на 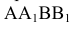
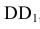
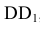
Фронтальная проекция 2» точки 2, лежащей на грани 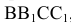
Рисунок 6.4 — Точка и прямая на поверхности наклонной призмы
Недостающую проекцию точки 3, расположенную на ребре 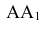
Нахождение недостающих проекций точек, находящихся на боковой поверхности прямой призмы (рис.6.5) упрощается, т.к. боковые грани призмы являются горизонтально-проецирующими плоскостями. Так горизонтальная проекция 1′ точки 1, расположенной на грани 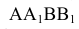
Рисунок 6.5 — Точка и прямая на поверхности прямой призмы
На рис. 6.6 показано построение недостающих проекций точек, находящейся на боковой поверхности пирамиды SABC. Фронтальная проекция 1″ точки 1, расположенная на грани SBC, представляющей собой профильно-проецирующую плоскость, построена с помощью линий связи.
Чтобы определить по заданной проекции 2″ точки 2, лежащей на грани SAB, проекцию 2′ (рис.6.4), используем горизонталь h.
Фронтальная проекция горизонтали h» проведена через проекцию 2″ до пересечения с проекцией B»S» ребра BS в точке D». Горизонтальная проекция h» горизонтали h проходит через точку D’ параллельно проекции A’B’ стороны AB.
Рисунок 6.6 — Точка и прямая на поверхности пирамиды
Додекаэдр — правильный двенадцатигранник. Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.
Способ граней
Суть способа сводится к последовательному определению линий пересечения двух плоскостей, одна из которых является заданной, а другая — какой-либо гранью многогранника (см. разд. 6). Для построения же самой фигуры сечения определяют точки пресечения найденных прямых, которые являются вершинами многоугольника сечения.
Способ ребер
Этот способ заключается в определении точек встречи прямых (ребер) с заданной плоскостью (см. разд. 7). Установив последовательно для всех ребер точки встречи их с секущей плоскостью, соединяют эти точки отрезками прямых и получают многоугольник сечения.
Развертки многогранников
В инженерном деле многогранники чаще всего реализуются как оболочки заданных форм и размеров. Для их изготовления необходимо уметь выполнить развертку (выкройку) таких оболочек. Развёртка многогранника представляет собой плоскую фигуру, полученную последовательным совмещением всех граней многогранника с плоскостью чертежа таким образом, чтобы грани примыкали друг к другу по линиям сгиба (рёбрам).
Для построения развёртки многогранника необходимо знать натуральные величины всех его граней, поэтому задача построения развертки многогранника решается в два этапа:
- определяют натуральную величину каждой грани (см. разд. 9);
- потом путем вращения вокруг соответствующей линии (ребра) (см. разд. 9) совмещают грани с плоскостью чертежа.
Примеры решения задач
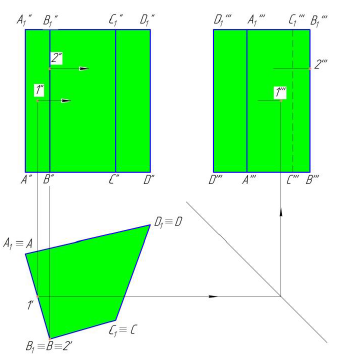
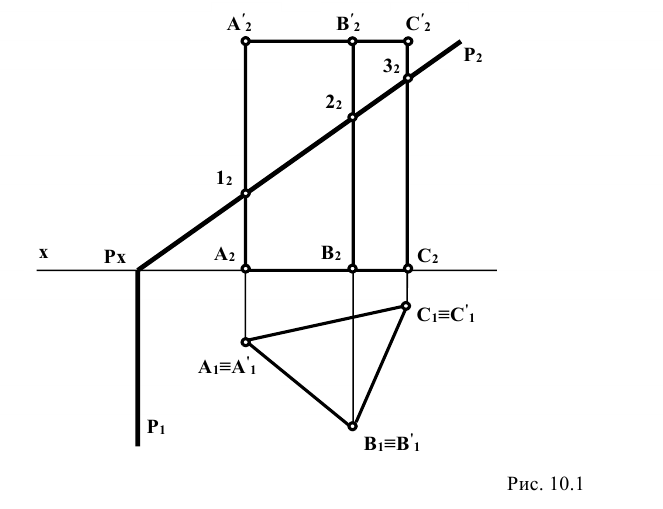
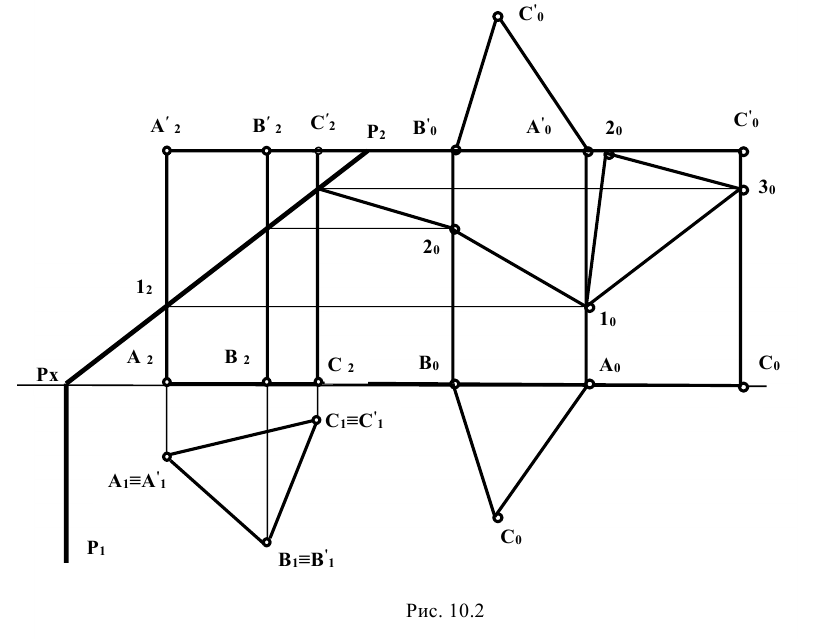
Задание: определить сечение трёхгранной призмы (рис. 10.1) плоскостью 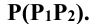
Решение: секущая плоскость Р является фронтально проецирующей и пересекает все рёбра прямой призмы 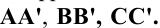
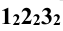
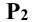
Рёбра призмы 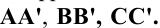
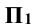
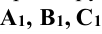
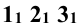
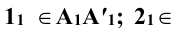
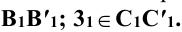
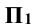
Для построения развёртки призмы совмещают ее боковые грани с фронтальной плоскостью проекций 
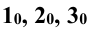
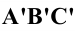
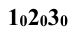
Видео:Развертка пирамидыСкачать

Что такое многогранник
Многогранники относятся к поверхностям, точнее — к гранным поверхностям, грани которых являются плоскостями. В связи с этим целесообразно выделить их в отдельную главу.
Многогранниками называются тела, ограниченные плоскими п-угольниками, которые называются гранями. Линии пересечения граней называются ребрами, точки пересечения ребер — вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В — Р = 2.
На рисунке 7.1 приведена классификация многогранников. Большую группу многогранников составляют правильные и полуправильные многогранники. Они характеризуются одинаково правильными гранями, одинаковым числом ребер, сходящихся в вершинах, и одинаковыми многогранными углами при вершинах. Полуправильные многогранники -это правильные многогранники со срезанными вершинами.
Выпуклыми многогранниками называются многогранники, располагаемые по одну сторону каждой грани. Если это не соблюдается, то многогранники называются вогнутыми или выпукло-вогнутыми.
Приведем примеры некоторых правильных многогранников. Тетраэдр — это четырехгранник, все грани которого равносторонние треугольники. Гексаэдр (куб) — шестигранник, все грани которого квадраты. Октаэдр — восьмигранник, все грани которого равносторонние треугольники. Додекаэдр — двенадцатигранник, все грани которого правильные пятиугольники. Икосаэдр — двадцатигранник, все грани которого равносторонние треугольники.
Наиболее распространенными в технике многогранниками являются правильные и неправильные, прямые и наклонные призмы и пирамиды. Призмой называется многогранник, в основаниях которого находятся плоские n-угольники, а остальные грани являются в общем случае параллелограммами. Пирамидой называется многогранник, в основании которого находится плоский п — угольник, а боковыми гранями являются треугольники с общей вершиной.
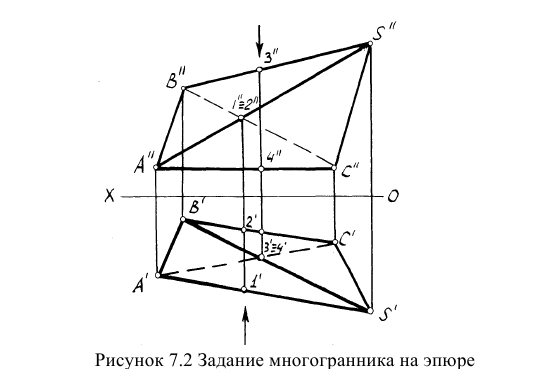
На эпюре многогранники задаются проекциями ребер, так называемой сеткой ребер. Поверхность многогранников считается геометрически непрозрачной, в связи с чем на эпюре следует определить видимость ребер методом конкурирующих точек (прямых). На рисунке 7.2 показан пример задания многогранников на эпюре и определения видимости ребер.
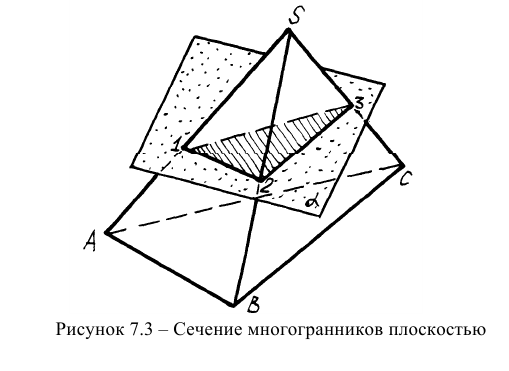
Пересечение многогранников плоскостями
Типовой задачей для многогранников является задача о пересечении многогранников плоскостями частного и общего положения (рисунок 7.3).
В обоих случаях задача может быть решена двумя методами, основанными на типичных позиционных задачах: методом ребер и методом граней.
В методе ребер несколько раз (по числу пересекаемых ребер) решается задача о пересечении прямой (ребра) с плоскостью (секущей плоскостью). В этом случае находятся точки 1,2,3— Найденные точки являются вершинами многоугольника сечения. В методе граней несколько раз решается типичная задача о пересечении двух плоскостей (граней многогранника и секущей плоскости) и находят линии 1-2, 2-3, 3-1, которые являются сторонами многоугольника сечения. Если секущая плоскость является плоскостью частного положения, то задача решается упрощенно.
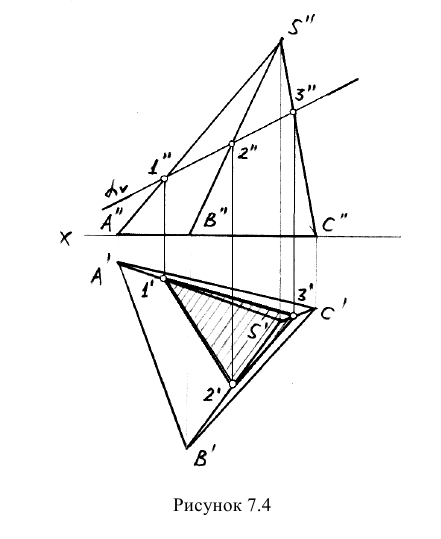
Пример: Построить сечение пирамиды фронтально-проецирующей плоскостью (рисунок 7.4).
Решение: Решаем задачу методом ребер. Так как секущая плоскость является фронтально-проецирующей, то на фронтальной проекции можно сразу определить точки встречи ребер пирамиды с секущей плоскостью — точки 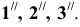
Пример: Построить сечение пирамиды плоскостью общего положения, определить его натуральную величину и построить развертку пирамиды с нанесением на неё линий сечения.
Решение: На рисунке 7.5 представлено решение задачи. Секущая плоскость рассекает пирамиду, начиная с основания пирамиды АВС. Горизонтальный след плоскости и горизонтальная проекция основания пересекаются в точках
Ребро пирамиды SA с секущей плоскостью не пересекается. Точки пересечения ребер SB и SC найдем как точки встречи прямых с плоскостью при помощи вспомогательных фронтально-проецирующих плоскостей 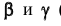
Натуральную величину сечения найдем методом совмещения (см. тему «Метод совмещения»). Для построения развертки пирамиды определим натуральную величину ребер SB и SC методом вращения вокруг горизонтально-проецирующей оси, проходящей через вершину пирамиды S (см. раздел «Метод вращения вокруг проецирующих осей»). Точки 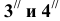
Развертку пирамиды построим методом раскатки (см. раздел «Развертки многогранников»).
Пересечение прямой с многогранником
Решение задачи о пересечении прямой с поверхностью многогранника осуществляется по методике, аналогичной методике решения задачи о пересечении прямой с плоскостью (см. рисунок 7.3). Через прямую проводят вспомогательную плоскость частного положения, строят сечение многогранника вспомогательной плоскостью и находят общие точки прямой и построенного сечения. Полученные точки являются точками встречи прямой с поверхностью многогранника (точки входа и выхода). Таким образом, задача сводится к решению задачи о построении сечения многогранника плоскостью частного положения, которая рассмотрена выше (см. рисунок 7.4).
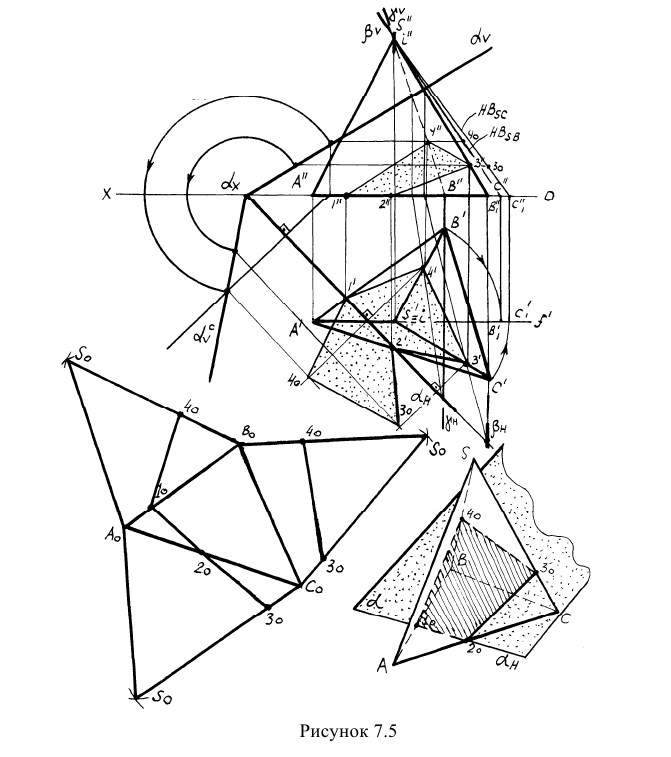
Взаимное пересечение многогранников
Задача о пересечении многогранников также решается методом ребер или методом граней в соответствие с рисунком 7.3. При пересечении многогранников возможны два случая: полное и неполное пересечение (рисунок 7.6).
Линия пересечения многогранников (или линии пересечения при полном пересечении) находится по следующему плану:
- 1) Определяют ребра, не участвующие в пересечении;
- 2) Определяют точки пересечения ребер первого многогранника с гранями второго многогранника;
- 3) Определяют точки пересечения ребер второго многогранника с гранями первого многогранника;
- 4) Полученные точки соединяют прямыми линиями в пределах каждой грани.
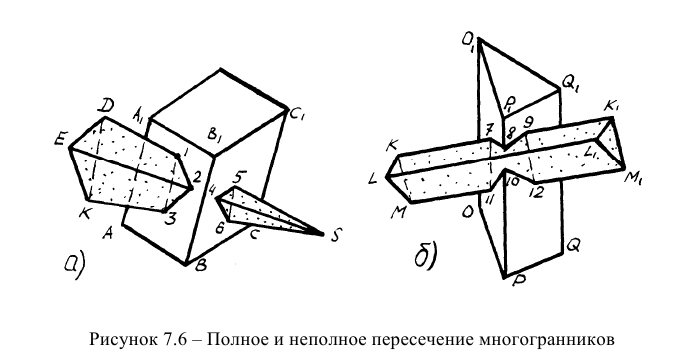
Пример: Построить линию пересечения пирамиды и призмы (рисунок 7.7).
Решение: Призма KLMN расположена в частном положении и её грани представляют из себя горизонтально-проецирующие плоскости. В связи с этим на горизонтальной проекции можно найти точки пересечения ребер пирамиды SB и SC с гранями призмы (точки 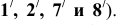
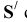
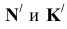
Далее соединим полученные точки в последовательности 1-2-3-5-7-8-6-4-1, которая определяется по горизонтальной проекции. Видимость проекций определим методом конкурирующих прямых.
Развертки многогранников
Любая техническая конструкция, имеющая форму многогранника (бункеры, короба, основания, полые перекрытия и т.д.), может быть изготовлена из листового материала, в связи с чем необходимо иметь развертку поверхности многогранника для раскроя и вырезки материала.
Разверткой поверхности называется геометрически закономерное преобразование поверхности в плоскость. Наиболее распространенными способами построения разверток поверхностей являются метод нормального сечения и метод раскатки. Прежде чем воспользоваться этими методами, необходимо определить натуральную величину ребер и оснований многогранника.
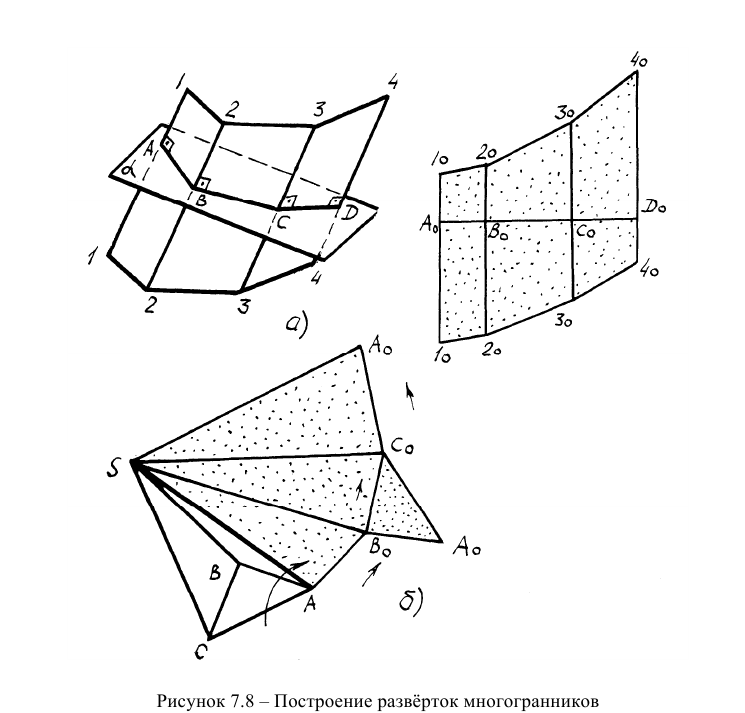
Метод нормального сечения (рисунок 7.8а) заключается в том, что поверхность многогранника (например, призмы) рассекают плоскостью, перпендикулярной ребрам, определяют натуральную величину сечения, совмещают стороны сечения в одну линию и к ней перпендикулярно пристраивают ребра по обе стороны линии.
Метод раскатки заключается в том, что к одной произвольной грани пристраивают поочередно соседние грани и основания, предварительно определив НВ ребер и оснований (рисунок 7.86). В примере 7.2 приведено построение развертки пирамиды методом раскатки (см. рисунок 7.5).
Пересечение пирамиды проецирующими плоскостями
Общие сведения. При пересечении многогранника плоскостью в сечении получается многоугольник, вершинами которого являются точки пересечения ребер многогранника плоскостью, а сторонами – отрезки прямых, по которым грани многогранника пересекаются этой плоскостью.
Определение вершин многоугольника сводится к построению точек пересечения прямых (ребер многогранника) с плоскостью – способ ребер.
При определении сторон многоугольника решаются задачи на пересечение двух плоскостей – способ граней.
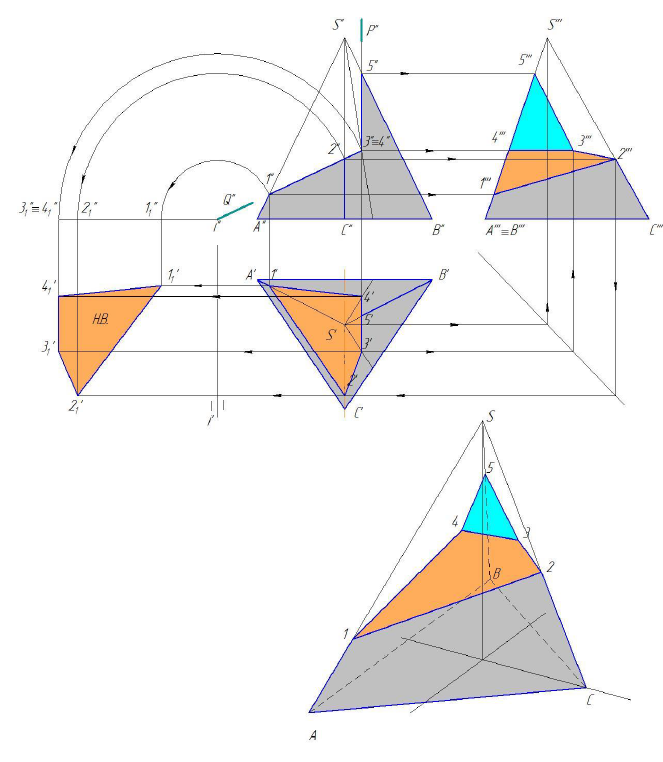
На рисунке 6.7 показано построение проекций линии пересечения прямой треугольной пирамиды фронтально – проецирующими плоскостями Q(Q’) и P(P’) [2].
Пересечение следа – проекции Q» с фронтальными проекциями боковых ребер призмы дает проекции 1»,2»,3»,4» вершин многоугольника сечения. Горизонтальные проекции этих вершин совпадают с «вырожденными» проекциями соответствующих ребер, так как призма прямая. Профильные проекции 1»,2»,3»,4» вершин определим при помощи горизонтальных линий связи на соответствующих проекциях ребер призмы.
Рисунок 6.7 – Построение проекций линии пересечения прямой треугольной пирамиды фронтально – проецирующими плоскостями
Плоскость Q пересекает грань SAC по отрезку 1-2, грань SBC по отрезку 2-3, грань SAB по отрезку 1-4.
Плоскость P пересекает грань SBC по отрезку 3-5, а грань SАB по отрезку 1-4. При построении проекций точек, принадлежащих линии пересечения, следует учитывать, что профильные проекции 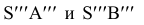
Недостающие проекции точки 1, расположенной на ребре SC, определены при помощи линий связи сначала на профильной проекции ребра, а затем на горизонтальной.
Для построения горизонтальных проекций точек 3 и 4, через их фронтальную проекцию проведены вспомогательные прямые SD и SE, принадлежащие соответственно граням SBC и SAB.
Построив горизонтальные проекции 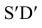
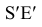
Плоскости Q и P пересекаются по фронтально-проецирующей прямой 3-4. Соединив построенные проекции точек получим проекции линии пересечения.
Натуральная величина многоугольника сечения найдена способом вращения вокруг фронтально-проецирующей оси.
Проекция 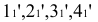
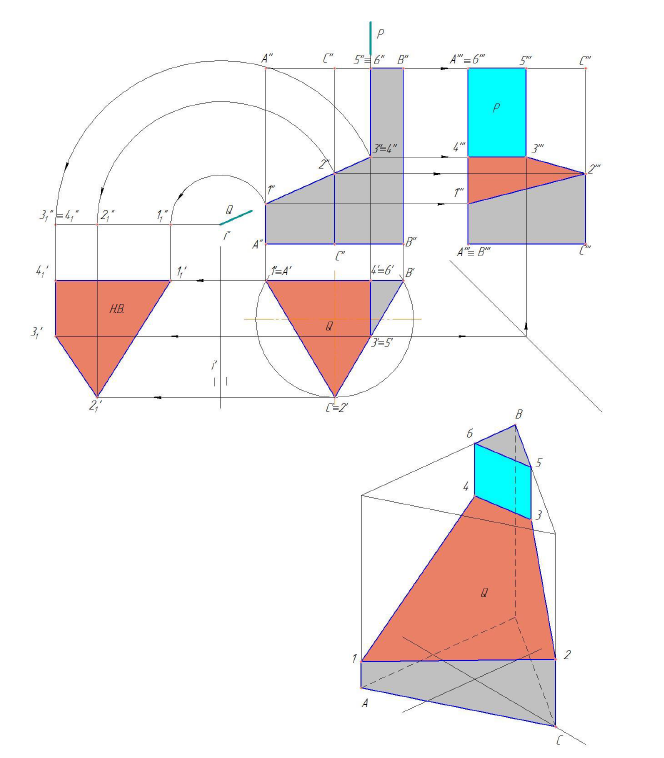
Пересечение призмы проецирующими плоскостями
Правильная треугольная призма усечена двумя плоскостями: фронтально-проецирующей 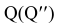
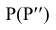
Построить профильную проекцию усеченной призмы.
Плоскость Q пересекает верхнее основание призмы по прямой 4-5, а боковую поверхность по горизонтально-проецирующим прямым 1-5 и 3-4.
Прямая 1-5 совпадает с ребром А призмы.
Плоскость Q пересекает ребро А призмы в точке 1, а ребро С–в точке 2.
Плоскости Q и P пересекаются по линии 1-3.
Профильные проекции указанных выше точек определяются при помощи линий связи. Соединив построенные точки получим профильную проекцию линии пересечения.
Рисунок 6.8 – Построение проекций линии пересечения прямой треугольной призмы фронтально – проецирующими плоскостями
Плоскости Q и P пересекаются по фронтально-проецирующей прямой 3-4. Соединив построенные проекции точек получим проекции линии пересечения.
Натуральная величина многоугольника сечения найдена способом вращения вокруг фронтально-проецирующей оси.
Проекция 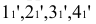
Видео:Пересечение многогранников. Пирамида с призматическим вырезом.Скачать

Многогранники и тела с кривыми поверхностями
В инженерной практике наиболее часто приходится иметь дело с геометрическими телами, которые условно можно подразделить на многогранники и тела с кривыми поверхностями.
Многогранник представляет собой тело, ограниченное со всех сторон плоскими многоугольниками (гранями). Пересекаясь друг с другом, грани образуют ребра, а те, в свою очередь, на сходящихся концах — вершины. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой грани, и правильным, если все его грани, плоские и многогранные углы равны между собой. Типичными представителями многогранников являются пирамида и призма.
Пирамида — многогранник, одной из граней которой служит многоугольник (основание), а другими — треугольники с общей вершиной. У призмы две грани — многоугольники (основания), а остальные грани — параллелограммы.
Кривую поверхность можно представить как траекторию движения некоторой линии (образующей) в пространстве. Образующая может быть прямой или кривой линией. Если поверхность образуется движением прямой, то она называется линейчатой, если кривой, то нелинейчатой. Примерами простейших линейчатых поверхностей являются конус и цилиндр.
Конус — геометрическое тело, образуемое движением прямой линии, проходящей через некоторую неподвижную точку (вершину), и плоским основанием. Цилиндр — геометрическое тело, которое образуется при движении прямой линии параллельно самой себе, с плоскими основаниями.
Рассмотрим построение сечения многогранников и линейчатых поверхностей плоскостью, а также точек пересечения прямой линии с этими геометрическими телами.
Пересечение многогранника плоскостью
В общем случае сечение многогранника плоскостью представляет собой плоскую замкнутую ломаную линию. Построение сечения возможно двумя способами:
- способом граней — найти линии пересечения граней с заданной плоскостью;
- способом ребер — найти точки встречи ребер пирамиды с плоскостью и последовательно соединить их.
Последний способ несколько проще, поэтому рассмотрим ход построения сечения многогранника именно этим способом на примере наклонной пирамиды 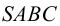
Находим точку пересечения ребра 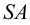
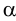
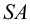
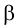
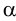
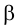
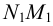
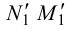
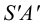
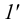
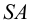
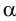
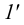
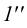
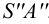
Аналогично находим проекции точки 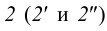
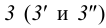
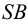
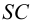
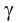
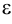
Соединив 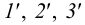
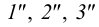
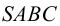
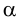
Пересечение конуса и цилиндра плоскостью
Для построения сечения конуса или цилиндра плоскостью в нее необходимо вписать многогранник (соответственно пирамиду или призму), построить сечение вписанного многогранника плоскостью, а затем полученные на ребрах многогранника точки соединить плавной кривой линией по лекалу. В результате получаем приближенное решение задачи, точность которого будет определяться числом граней вписанного многогранника (для обеспечения достаточной точности вписанного многогранника должно быть не менее шести граней).
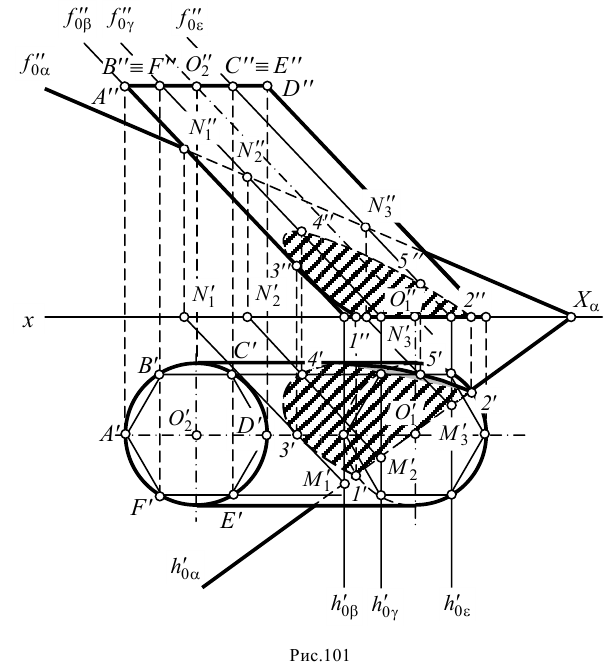
На рис.101 построено сечение наклонного цилиндра плоскостью 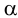
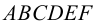
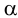
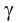
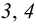
На плоскости проекций 
Пересечение прямой линии с поверхностью многогранника
Для построения точек пересечения прямой линии с поверхностью многогранника необходимо:
- через прямую провести любую вспомогательную плоскость;
- построить сечение многогранника этой вспомогательной плоскостью;
- найти искомые точки в пересечении прямой с контурами построенного сечения.
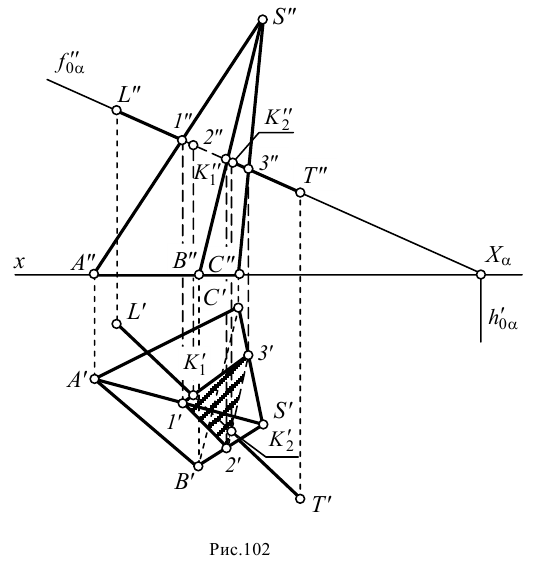
Рассмотрим построение точек встречи на примере пересечения прямой 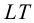
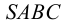
Поскольку через прямую линию можно провести любую плоскость, нам удобнее воспользоваться плоскостью частного положения. Проводим через прямую 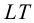
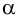
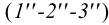
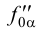
Далее строим горизонтальную проекцию сечения 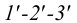
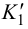
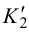
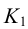
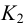
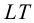
На рис.102 показана также видимость прямой относительно поверхности пирамиды. На плоскости 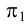
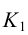
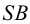
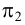
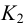
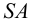
Пример:
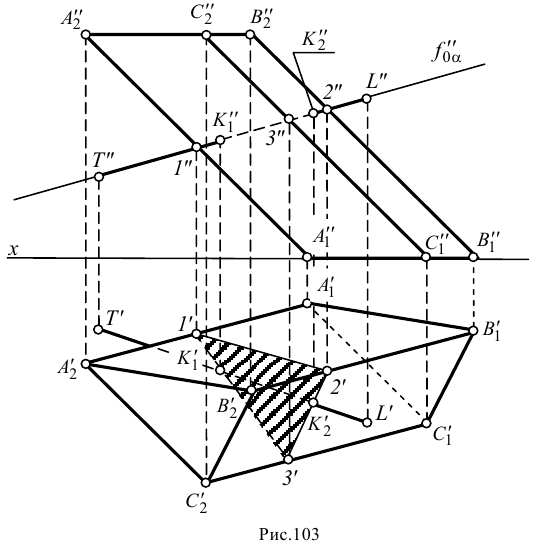
Построить точки пересечения прямой 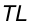
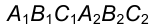
Точки встречи прямой 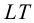
Через заданную прямую проводим вспомогательную плоскость, например фронтально-проецирующую плоскость 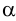
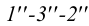
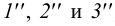
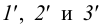
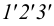
Точки пересечения 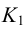
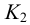
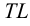
Определяем видимость прямой относительно поверхности призмы. В направлении на плоскость 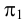
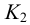
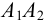
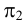
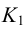
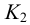
Пересечение прямой линии с поверхностью конуса и цилиндра
Точки пересечения прямой линии с поверхностью конуса или цилиндра можно построить двумя способами.
Первый способ заключается в том, что в конус или цилиндр вписывают соответственно пирамиду или призму, строят сечение вписанного многогранника вспомогательной плоскостью и полученные точки на ребрах соединяют плавной кривой. Точки пересечения прямой с построенным сечением есть точки пересечения этой прямой с поверхностью заданного геометрического тела. В результате получаем приближенное решение задачи.
Для получения точного решения вспомогательную плоскость нужно выбрать так, чтобы полученное сечение линейчатой поверхности представляло собой простейшую фигуру — многоугольник. В случае конической поверхности такая плоскость должна проходить через заданную прямую и вершину конуса, тогда в сечении образуется треугольник.
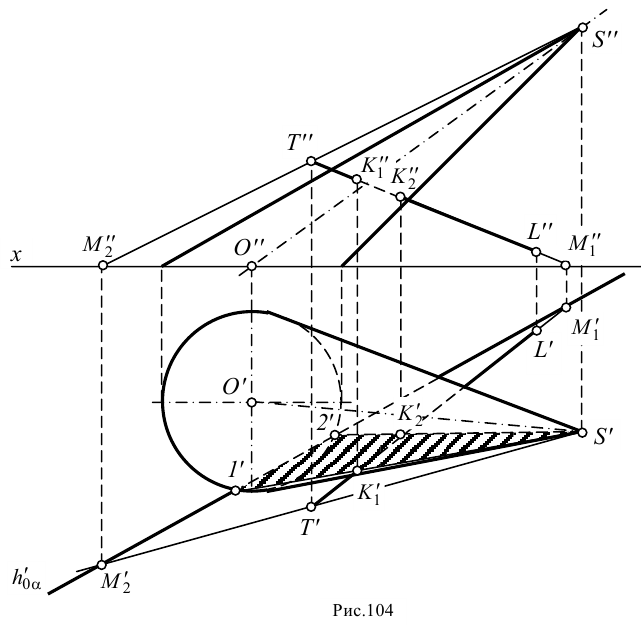
Используем последний способ для построения точек пересечения наклонного кругового конуса прямой 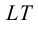
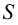
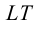
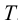
Теперь вспомогательная плоскость (общего положения) оказывается заданной двумя пересекающимися прямыми 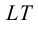
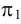
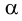
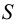
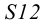
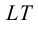
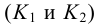
На рис.105 показано нахождение точек пересечения прямой с поверхностью цилиндра. В этом случае в качестве вспомогательной плоскости выбираем плоскость общего положения, параллельную оси цилиндра, и задаем ее двумя пересекающими прямыми — прямой 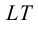
Такую произвольную прямую можно провести через любую точку прямой 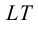
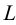
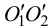
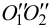
Теперь, как и в предыдущем примере, строим горизонтальный след 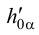
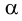
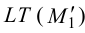
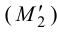
В точках 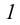
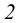
Построение разверток поверхностей
Развертка поверхности представляет собой фигуру, образуемую при совмещении поверхности геометрического тела с плоскостью чертежа. Существует два подхода к построению разверток поверхностей. Первый заключается в определении геометрических размеров развертки путем алгебраических вычислений. Таким способом легко развертывается поверхность прямого кругового конуса и прямого кругового цилиндра. Второй способ — графический.
Все поверхности делят на развертываемые и неразвертываемые.
Развертываемой называют поверхность, которая при совмещении с плоскостью чертежа не претерпевает каких-либо повреждений (разрывов, складок и т.д.). На развертке таких поверхностей сохраняется длина линий, лежащих на поверхности, размер углов между линиями и площади фигур, образованных замкнутыми линиями. Все размеры на развертке имеют натуральную величину. К развертываемым поверхностям относят все многогранные поверхности (пирамиды, призмы и т.д.) и некоторые линейчатые поверхности (конус, цилиндр).
Неразвертываемой называют поверхность, которая при совмещении с плоскостью претерпевает какие-либо искажения. У неразвертываемых поверхностей разверток быть не может, однако на практике в отдельных случаях возникает необходимость в построении приближенной «развертки» таких поверхностей. К неразвертываемым поверхностям относят все нелинейчатые поверхности (сфера, эллипсоид и др.).
Развертка поверхности пирамиды
Развертка полной поверхности 
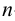
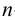
На рис.106 показано построение развертки наклонной треугольной пирамиды 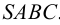
Ребра пирамиды 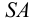
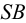
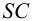
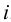
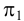
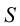
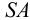
Ребро 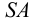
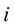
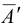
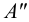
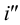
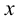
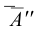
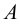
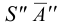
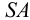
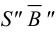
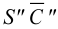
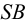
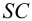
Строим треугольники, составляющие грани пирамиды 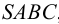
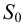
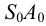
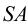
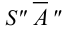
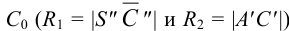
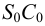
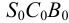
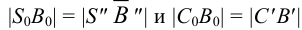
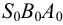
Построенную развертку боковой поверхности пирамиды дополняем основанием — треугольником 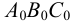
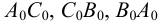
Рассмотрим построение на развертке некоторой точки 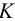
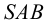
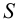
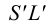
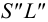
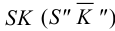
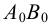
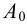
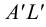
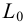
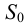
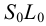
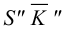
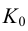
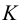
Развертка поверхности призмы
Развертка поверхности прямой призмы строится весьма просто: развертка ее боковой поверхности представляет собой ряд прямоугольников с общими сторонами. В этом случае построение развертки сводится к определению натуральных величин основания призмы и одного ребра.
Развертка полной поверхности 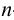
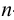
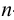
Для построения развертки наклонной призмы можно использовать два способа — нормального сечения и раскатки. Строго говоря, метод треугольников также может быть применен для построения развертки поверхности призмы, у которой все грани предварительно разбиты на треугольники. Однако на практике построение развертки призмы этим методом проводится крайне редко в связи с необходимостью выполнения многочисленных построений. Если основания призмы проецируются с искажением, то для построения развертки следует предпочесть метод нормального сечения. Если же основания на одну из плоскостей проекций проецируются в натуральную величину, то целесообразнее воспользоваться методом раскатки.
Метод нормального сечения (сечения, перпендикулярного ребрам призмы) состоит из следующих построений:
- поверхность многогранника пересекают плоскостью, перпендикулярной его ребрам;
- определяют натуральную величину нормального сечения;
- находят натуральную величину ребер многогранника;
- на свободном месте чертежа контур нормального сечения развертывают в отрезок прямой;
- через концы отрезков проводят перпендикуляры, на которых откладывают натуральные величины отрезков ребер;
- концы перпендикуляров соединяют;
- к построенной развертке боковой поверхности призмы пристраивают основания.
На рис.107 и 108 показано построение развертки треугольной наклонной призмы 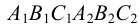
Поскольку горизонтальные проекции ребер призмы параллельны оси 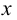
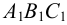
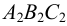
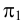
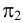
Заданная призма рассечена вспомогательной фронтально-проецирующей плоскостью 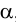
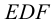
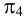
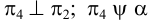
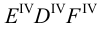
На чертеже (рис.108) треугольник 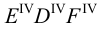
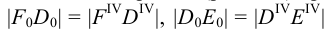
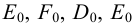
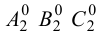
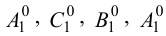
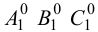
Для нанесения на развертку некоторой точки 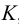
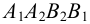
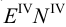
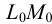
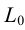
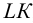
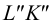
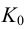
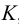
Метод раскатки состоит в том, что призму последовательно вращают вокруг ее ребер до совмещения граней с плоскостью чертежа. Пример построения развертки поверхности призмы 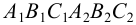
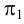
Решение задачи начнем с определения натуральных величин ребер призмы. Для этого введем дополнительную плоскость проекций 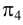
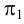
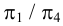
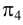
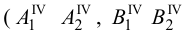
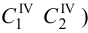
Рассмотрим последовательное вращение призмы в положение, при котором ее грани совмещаются с плоскостью чертежа (а точнее, с плоскостью, параллельной плоскости проекций 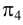
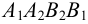
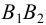
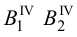
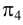
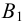
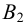
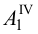
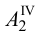
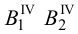
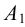
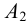
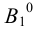
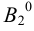
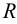
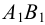
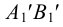
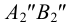
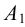
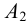
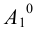
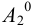
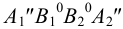
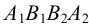
Аналогично построены точки 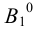
На рис.109 найдено также положение на развертке точки 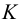
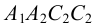
Развертка поверхности конуса
Разверткой боковой поверхности прямого кругового конуса является сектор, радиус которого равен длине образующей конуса 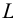
где 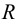
Пример 25. Построить развертку прямого кругового конуса и нанести на нее линию пересечения фронтально-проецирующей плоскостью 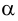
1. Основание конуса разобьем на 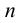
2. На поверхность конуса нанесем ряд образующих 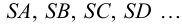
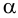
3. Вычерчиваем развертку боковой поверхности конуса — круговой сектор радиусом 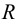
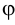
4. Разбиваем дугу сектора 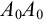
5. Методом вращения вокруг оси конуса определяем натуральные величины отрезков всех образующих между вершиной 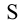
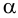
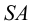
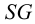
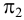
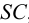
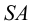
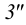
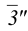
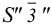
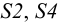
6. Откладываем истинные величины расстояний от точки 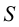
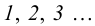
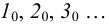
В общем случае для построения развертки поверхности наклонного конуса в него вписывают пирамиду, ребра которой равны отрезкам образующих конуса, и строят развертку поверхности этого многогранника. Построенные на развертке вершины основания пирамиды соединяют по лекалу плавной кривой линией, а крайние точки связывают с вершиной конуса отрезками прямой линии. Построенная развертка тем точнее, чем больше граней у пирамиды, вписанной в конус.
Для получения полной развертки поверхности конуса развертку боковой поверхности дополняют фигурой, лежащей в основании конуса. Если основание конуса не параллельно плоскости проекций и не лежит в ней, то для построения его на развертке первоначально необходимо найти натуральную величину этой фигуры.
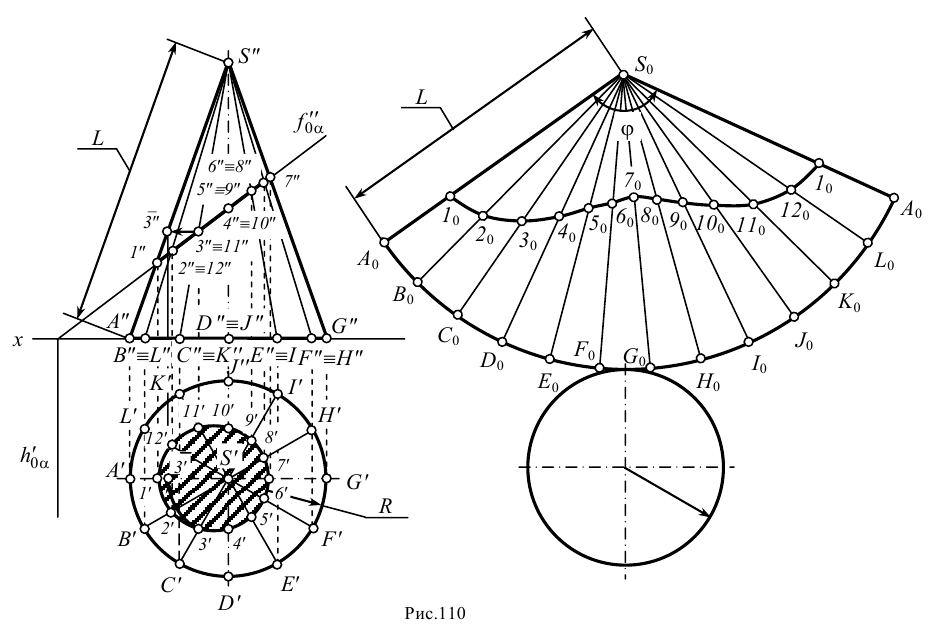
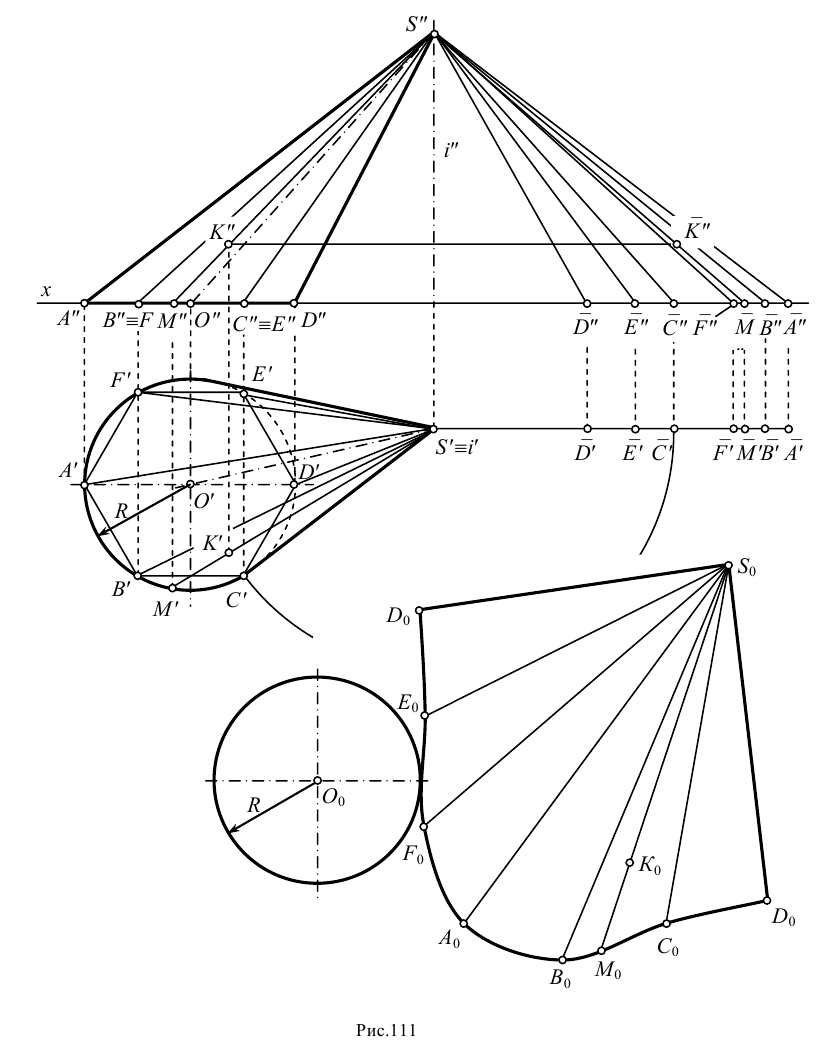
На рис.111 дан пример построения развертки наклонного кругового конуса. В конус вписана шестиугольная пирамида, основанием которой является правильный шестиугольник 
Развертку поверхности пирамиды строим методом треугольников. Через найденные на развертке точки 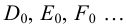
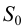
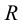
Для построения на развертке точки, заданной на поверхности конуса, например точки 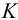
Развертка поверхности цилиндра
Фигура, образуемая при развертывании поверхности цилиндра, представляет собой «отпечаток», полученный при качении цилиндра по плоскости чертежа. Если цилиндр — прямой, то эта фигура является прямоугольником, ширина которого равна длине образующей цилиндра, а длина равна 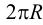
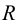
Если цилиндр наклонный, то фигура, образуемая при развертывании его поверхности, ограничена двумя кривыми линиями (синусоидами), концы которых соединены отрезками.
В общем случае развертку поверхности цилиндра строим путем замены поверхности цилиндра поверхностью вписанной в него призмы, ребра которой равны отрезкам образующих цилиндра. Обычно при построении развертки поверхности цилиндра в него вписывают правильную призму, так как при этом упрощаются построения, связанные с разметкой развернутых контуров основания. Развертка поверхности тем точнее, чем больше граней у вписанной в цилиндр призмы.
Построенная развертка поверхности дополняется основаниями цилиндра. При этом если основания проецируются на плоскости проекций с искажением, то перед их нанесением на развертку предварительно необходимо найти натуральную величину этих фигур.
Развертка поверхности призмы, вписанной в цилиндр, строится или методом нормального сечения, или методом раскатки. В обоих случаях для развертывания поверхности необходимо, чтобы ребра вписанной в цилиндр призмы были параллельны одной из плоскостей проекций.
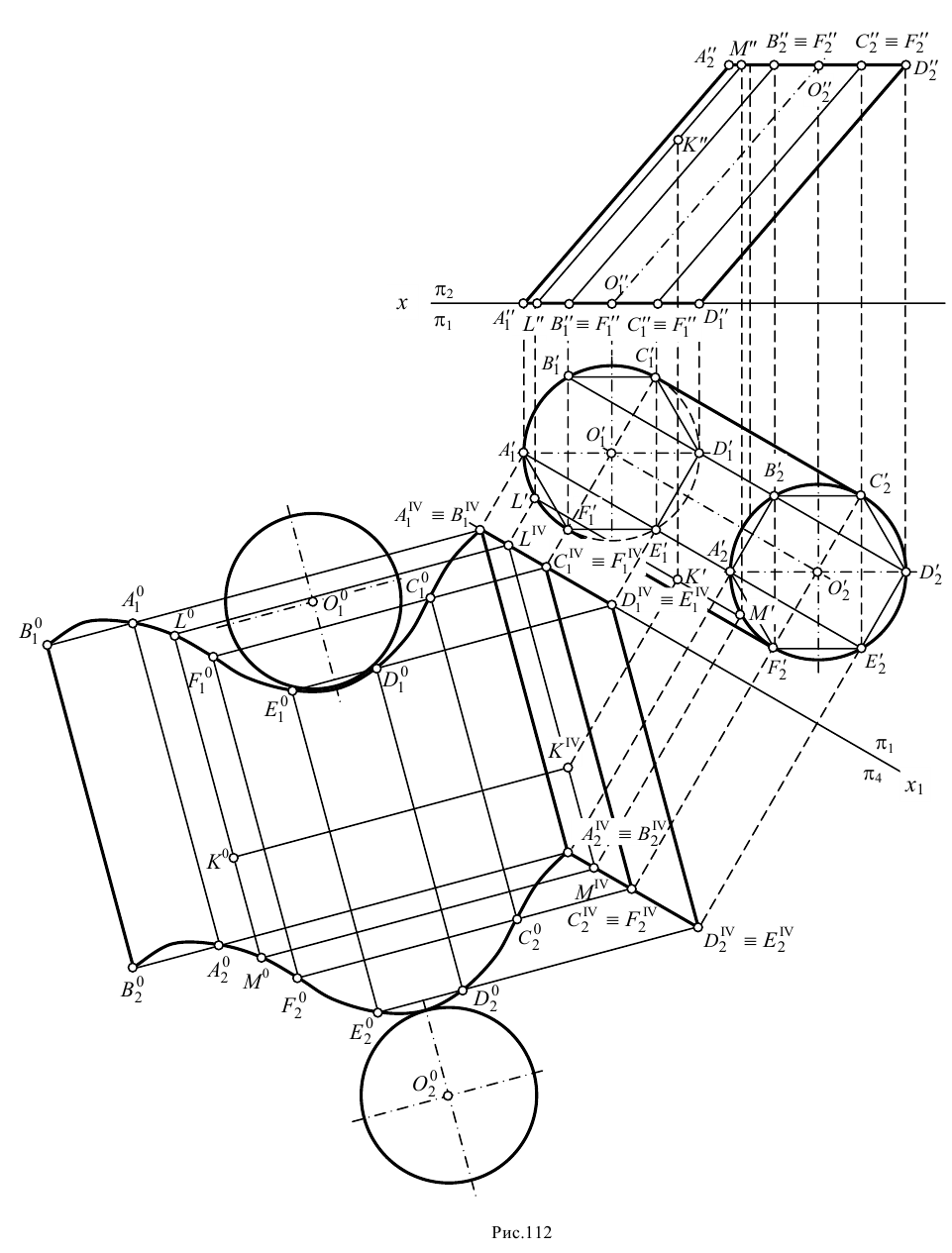
Рассмотрим построение развертки наклонного кругового цилиндра, изображенного на рис.112. В цилиндр вписана правильная шестиугольная призма. Основания как заданного цилиндра, так и вписанной в нее призмы проецируются на плоскость 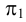
Поскольку ребра призмы являются отрезками прямых общего положения, ее проекция преобразована путем введения дополнительной плоскости проекций 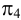
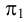
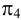
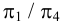
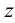
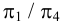
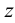
Затем определена натуральная величина грани 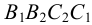
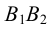
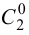
Построения повторяются до тех пор, пока все грани призмы не станут параллельны плоскости 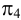
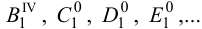
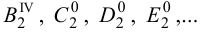
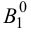
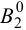
Если на развертку необходимо нанести точку, принадлежащую поверхности цилиндра (например, точку 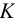
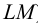
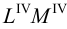
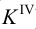
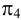
Взаимное пересечение геометрических тел
При взаимном пересечении геометрических тел образуется геометрическое место точек, принадлежащих одновременно обеим поверхностям. Оно представляет собой линию пересечения данных поверхностей.
Способ построения линии пересечения зависит, прежде всего, от вида пересекающихся поверхностей. Возможны следующие типы взаимного пересечения:
- поверхностей многогранников;
- поверхностей вращения и многогранника;
- поверхностей вращения.
Взаимное пересечение поверхностей многогранников
При пересечении поверхностей двух многогранников образуется одна или несколько пространственных замкнутых ломаных линий (в частном случае — плоская ломаная линия).
В зависимости от способа определения элементов линии пересечения (ее сторон или вершин) построение производится путем:
- определения отрезков прямых, по которым грани одного многогранника пересекают грани другого — способ граней;
- определения точек пересечения ребер первого многогранника с гранями второго и ребер второго многогранника с гранями первого — способ ребер.
Выбор способа зависит от расположения многогранников, возможно комбинированное использование обоих способов. На практике используют главным образом способ ребер.
Существуют следующие правила, которыми следует руководствоваться при построении линии пересечения:
- если хотя бы одна проекция ребра многогранника не пересекает проекцию грани другого многогранника, то данное ребро не пересекает этой грани (однако пересечение всех проекций ребра одного многогранника со всеми одноименными проекциями граней другого многогранника не означает, что эти ребро и грань пересекаются);
- проекции линии пересечения располагаются в пределах фигуры, образованной при наложении одноименных проекций двух многогранников;
- отрезок линии пересечения лежит в пределах пересекающихся граней как первого, так и второго многогранника (последовательность соединения точек линии пересечения определяется при помощи вспомогательных диаграмм или таблиц, например при помощи сетки Д.Г.Ананова);
- отрезок линии пересечения считается видимым, если он находится в видимых гранях обоих многогранников.
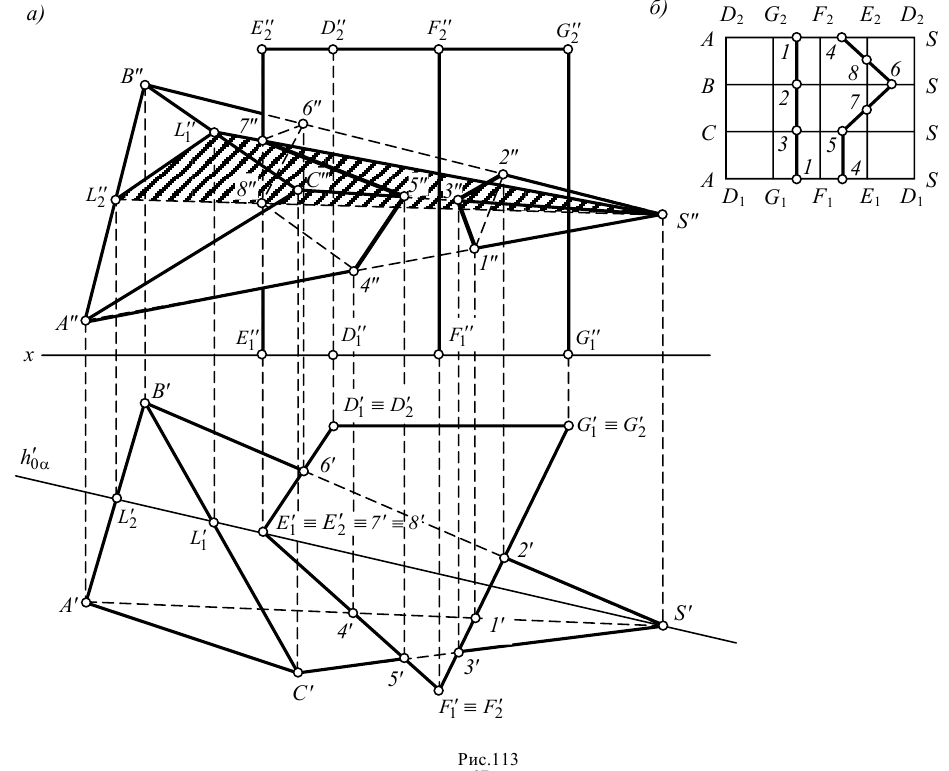
На рис.113, 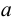
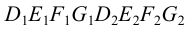
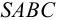
Проанализируем положение проекций ребер призмы относительно граней пирамиды. Фронтальные проекции обоих оснований призмы не пересекают проекцию пирамиды, следовательно, они не пересекают поверхность пирамиды. Горизонтальные проекции ребер призмы 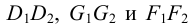
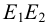
Рассуждая аналогично, можно прийти к выводу, что ребра 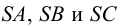
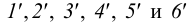
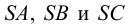
Для нахождения точек пересечения ребра 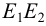
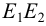
Последовательность соединения построенных точек определена при помощи сетки Д.Г.Ананова (рис.113, б) — таблицы, строки и столбцы которой схематично изображают грани и ребра пересекающихся многогранников. Столбцы 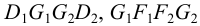
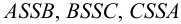
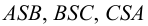
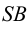
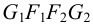
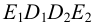
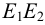
Таким образом, линия пересечения заданных многогранников распалась на две линии: треугольник 
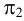
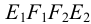
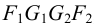
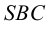
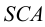
Пересечение поверхности вращения и поверхности многогранника
Линия пересечения таких поверхностей представляет собой одну или несколько плоских кривых линий, являющихся пересечением отдельных граней многогранника с заданным телом вращения. Точки излома кривой линии (если они имеются) соответствуют точкам пересечения ребер многогранника с поверхностью вращения.
В общем случае для построения линии пересечения необходимо найти ряд точек, принадлежащих обеим поверхностям, и соединить их замкнутой кривой линией. Эти точки могут быть найдены путем проведения:
- вспомогательных прямых линий, принадлежащих граням многогранника;
- вспомогательных образующих тела вращения;
- вспомогательных секущих плоскостей.
Как правило, общие точки определяют комбинацией перечисленных выше способов с учетом упрощения или уточнения построений. Построение линии пересечения начинается с определения характерных точек, т.е. точек, занимающих особое положение по отношению к плоскостям проекций или к самой линии пересечения.
К характерным относятся точки:
- наиболее удаленная и наиболее близкая к плоскостям проекций (экстремальные точки);
- делящие кривую на видимую и невидимую части (точки видимости);
- наибольшей или наименьшей ширины кривой.
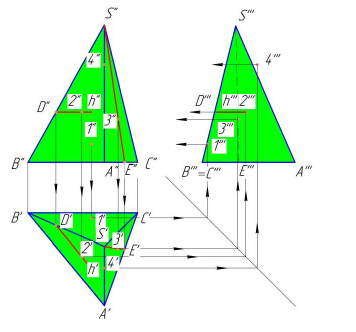
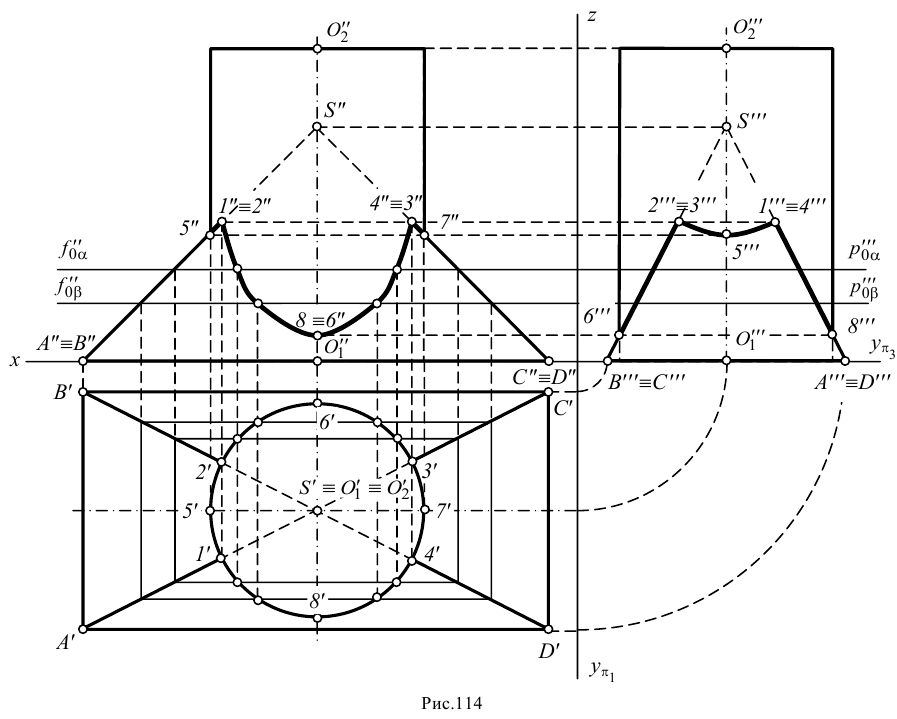
Рассмотрим пример построения линии пересечения правильной четырехугольной пирамиды и соосного с ней цилиндра (рис.114). Характерные точки 1, 2, 3 и 4, являющиеся точками встречи ребер пирамиды с поверхностью цилиндра, определены по пересечению горизонтальных проекций ребер с проекцией поверхности цилиндра (на горизонтальную плоскость проекций она спроецировалась в окружность).
Характерные точки 5, 6, 7 и 8, наиболее близкие к плоскости проекций 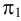
Дополнительные точки определены при помощи вспомогательных секущих плоскостей 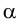
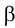
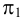
Построенные точки последовательно соединяют замкнутой кривой линией. Линия пересечения представляет собой четыре дуги (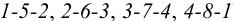
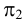
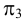
Взаимное пересечение поверхностей вращения
Линия пересечения поверхностей вращения является пространственной кривой линией (или кривыми линиями). Однако в некоторых частных случаях она может быть и плоской -окружностью, эллипсом, прямой и т.д.
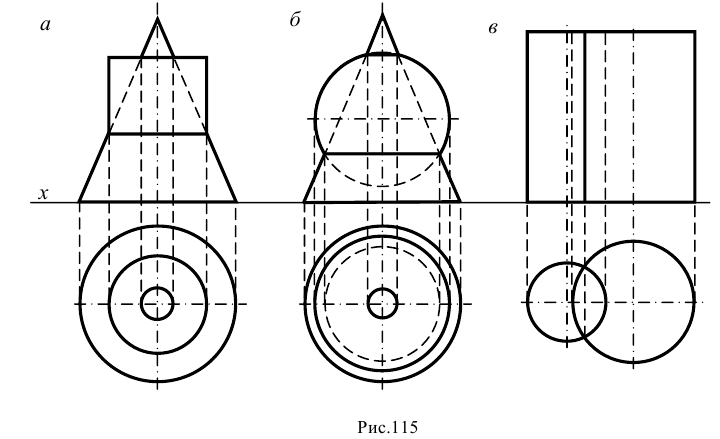
Рассмотрим простейшие случаи. Если две поверхности вращения имеют общую ось, то линия пересечения представляет собой окружность. На рис.115, а дан пример построения линии пересечения цилиндра, соосного с круговым конусом, а на рис.115, б — конуса и шара. В обоих случаях на фронтальную плоскость проекций линия пересечения спроецировалась без искажения в две концентрические окружности. На рис.115, в изображены два цилиндра с параллельными осями — линией пересечения являются общие образующие этих поверхностей.
В общем случае для построения линии пересечения необходимо найти ряд точек, принадлежащих обеим поверхностям, и затем последовательно соединить их кривой линией.
Для определения общих точек применяют два способа:
- вспомогательных образующих линий;
- вспомогательных секущих поверхностей.
В первом случае определяют точки, в которых образующая одной поверхности вращения пересекает другую поверхность. Повторяя этот прием для нескольких образующих, определяют ряд точек, необходимых для построения линии пересечения.
Во втором случае заданные тела пересекают третьей поверхностью, которая дает в пересечении с ними простейшие для построения линии (прямые или окружности). Точки взаимного пересечения этих линий лежат как на секущей поверхности, так и на поверхности заданных тел вращения. Проведя ряд секущих поверхностей, можно найти необходимое количество общих точек, через которые затем проводят искомую линию пересечения.
Способ вспомогательных образующих рационально использовать при построении линии пересечения поверхностей вращения, если хотя бы одна из заданных поверхностей является линейчатой и точки пересечения прямолинейных образующих с контурами второй поверхности очевидны.
Способ вспомогательных секущих поверхностей является более универсальным. На практике применяют следующие секущие поверхности:
- а) плоскости общего или частного положения (способ вспомогательных секущих плоскостей);
- б) кривые поверхности (в случае применения сфер — способ вспомогательных секущих сфер)
.
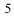
Иногда целесообразно комбинировать различные способы построения. Линия пересечения получается тем точнее, чем больше точек найдено для ее построения.
Существуют правила, которыми следует руководствоваться при построении линии пересечения:
- проекции линии пересечения наносят в пределах наложения проекций заданных поверхностей;
- при общем расположении поверхностей вращения для упрощения и уточнения построений их положение необходимо преобразовать в частное;
- построение линии пересечения начинают с определения ее характерных точек.
Рассмотрим построение линии пересечения прямых круговых конуса и цилиндра с параллельными осями способом вспомогательных секущих плоскостей (рис.116). Здесь действуют те же принципы, что и в рассмотренном выше примере взаимного пересечения поверхности вращения и многогранника.
Сначала определяют характерные точки линии пересечения. В пересечении видимой образующей конуса с поверхностью цилиндра лежит точка 1, наивысшая точка по отношению к плоскости 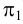
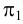
Таким образом, на фронтальной и профильной плоскостях проекций все точки линии пересечения должны находиться между точками 1 и 2 (3). Заданные геометрические тела рассекают вспомогательными горизонтальными плоскостями 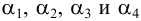
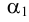
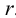
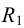
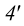
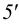
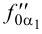
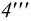
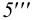
Аналогично находят ряд точек 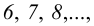
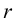
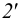
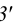
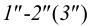
Видео:Начертательная геометрияСкачать
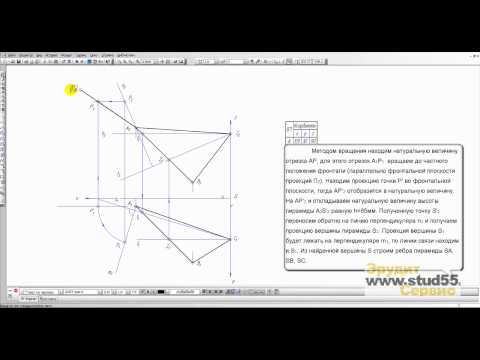
Способы задании многогранников и построение их проекций
Одним из видов пространственных форм являются многогранники. Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого. Вершины и стороны многоугольников являются вершинами и ребрами многогранников, а сами многоугольники — гранями. Мы будем рассматривать только выпуклые многогранники, т.е. такие, которые расположены по одну сторону плоскости любой из его граней.
Наибольший практический интерес представляют призмы и пирамиды. Призмой называется многогранник, две грани которого представляют собой равные многоугольники с взаимно параллельными сторонами — основаниями. Ребра, не принадлежащие основаниям и параллельные между собой, называют боковыми ребрами. Пирамидой называется многогранник, одна грань которого — многоугольник со сколь угодно большим числом сторон (не менее трех), а остальные грани являются треугольниками с общей вершиной.
Форма и положение многогранника в пространстве могут быть определены заданием его ребер, основанием и вершиной, если это пирамида, основанием и высотой, если это призма.
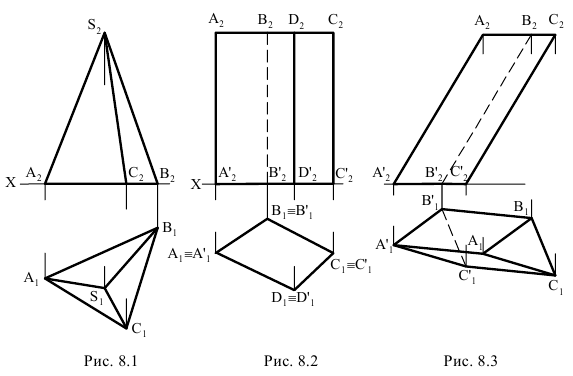
Выбирая положение пирамиды или призмы для их изображения, целесообразно располагать их основания параллельно плоскости проекций. Примеры приведены на рис. 8.1, 8.2, 8.3. Здесь в системе плоскостей проекций 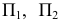
Как видно, пирамида задается на эпюре проекциями ее основания и вершины, а призма — проекциями основания и ребер.
Пересечение плоскости и прямой с многогранниками
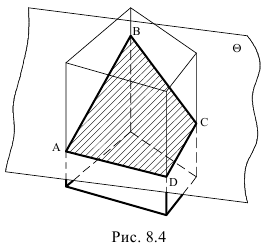
При пересечении многогранника плоскостью в общем случае получается плоский многоугольник 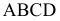
Плоскую фигуру, полученную от пересечения многогранника плоскостью, называют сечением
Рассмотрим несколько примеров.
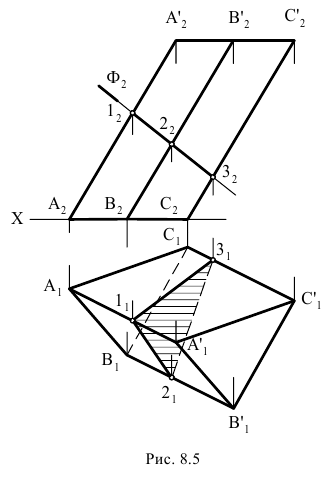
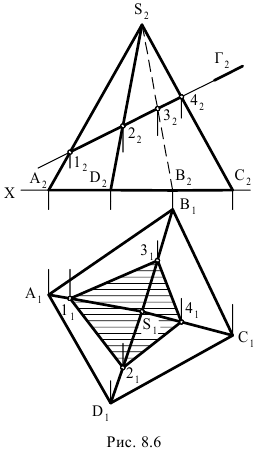
На рис. 8.5 построены проекции фигуры сечения наклонной трехгранной призмы фронтально проецирующей плоскостью
Фронтальными проекциями точек встречи ребер призмы с секущей плоскостью (фронтальными проекциями вершин фигуры сечения) являются точки 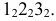
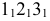
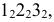
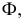
На рис. 8.6 построены проекции фигуры сечения четырехгранной пирамиды фронтально проецирующей плоскостью. Здесь, как и в предыдущем примере, фронтальная проекция сечения 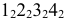
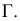
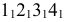
Если многогранник пересекает плоскость общего положения, то для определения линии пересечения необходимо воспользоваться некоторыми дополнительными вспомогательными построениями. Эти построения можно выполнятъ двумя способами:
- а) метод ребер — нахождение точек пересечения ребер многогранника с плоскостью, т.е. нахождение вершин многогранника, получающегося в сечении;
- б) метод граней — нахождение линий пересечения граней многогранника с секущей плоскостью, т.е. нахождение сторон сечения
Так, на рис. 8.7. линия пересечения призмы 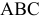
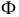
Горизонтальный след 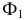
Ребро 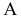
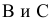
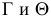
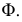
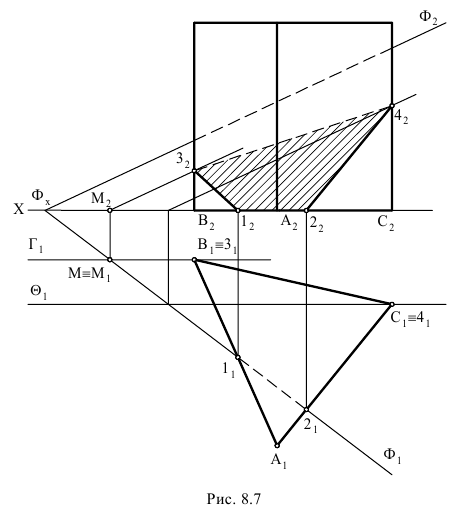
Использование метода граней показано на рис. 8.8, когда необходимо построить сечение призмы 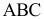
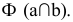
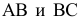
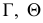
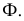
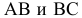
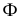
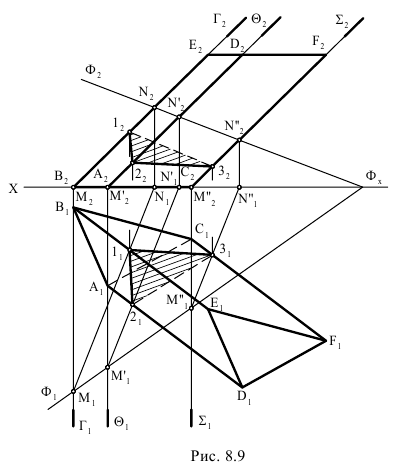
На рис. 8.9. построены проекции сечений плоскостью 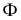
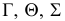
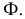
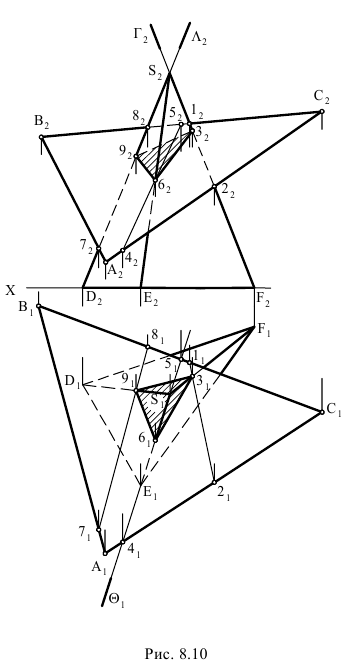
На рис. 8.10 построены проекции сечения плоскостью 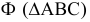
Задача решена нахождением точек встречи (точек 3, 6, 9) каждого ребра пирамиды с секущей плоскостью. Чтобы найти точку (3) встречи ребра 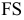
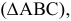
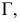
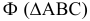
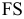
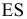
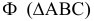
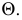
Прямая линия может пересекать поверхность многогранника в двух точках при условии, что многогранник выпуклый. Решение этой задачи основано на схеме определения точки пересечения прямой с плоскостью и распадается на три этапа:
- через заданную прямую проводится вспомогательная плоскость;
- строится проекция фигуры сечения многогранника;
- определяются точки пересечения прямой с контуром сечения.
На рис. S.11 построены точки 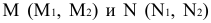
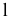
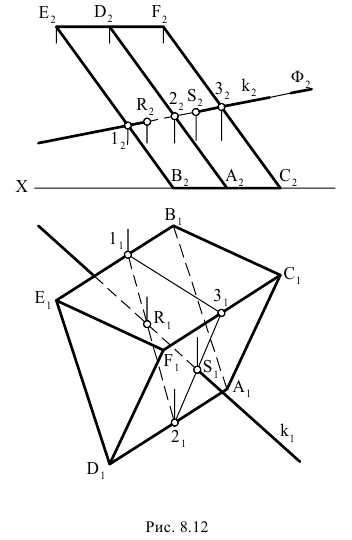
На рис. 8.12 построены точки 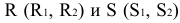
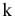
Взаимное пересечение многогранников
Многогранные поверхности пересекаются друг с другом по замкнутым ломаным линиям, для построения которых сначала находим точки пересечения ребер одного многогранника с гранями другого, а затем -ребер второго с гранями первого. Соединяя в определенной последовательности полученные точки, строим искомую ломаную, каждое звено которой представляет собой прямую пересечения двух граней — грани первого многогранника с гранью второго.
Итак, построение линии пересечения двух многогранников сводится к решению задачи на пересечение прямой линии с многогранником (или на взаимное пересечение двух плоскостей — граней многогранников).
На рис. 8.13 приведен пример построения линии взаимного пересечения прямой четырехугольной призмы с пирамидой
Основание призмы совмещено с плоскостью 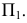
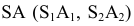
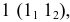
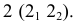
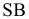
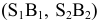
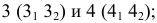
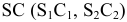
Из четырех вертикальных ребер призмы только одно пересекает пирамиду. Находим точки его пересечения с гранями пирамиды. Через это ребро и вершину 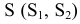
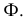
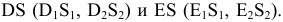
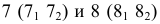
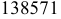
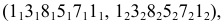
Видимыми являются только те из отрезков многоугольников пересечения, которые принадлежат видимым граням многогранников; невидимые отрезки обозначаем на эпюре штриховыми линиями
Отрезки 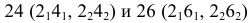
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Поверхности вращения
- Пересечение прямой линии с поверхностью
- Построение линии пересечения поверхностей
- Проецирование прямой
- Проекции с числовыми отметкам
- Гранные поверхности
- Проецирование точки
- Прямая в пространстве и ее изображение на чертеже
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

ПИРАМИДА в ИЗОМЕТРИИСкачать
Лекция 5 Задача 4Скачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Как найти высоту пирамиды. Начертательная геометрияСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Как начертить ПИРАМИДУ в объемеСкачать
Построение сечения пирамиды по трем точкамСкачать

Пирамида с вырезомСкачать
Комплексный чертеж усеченной 5-гранной пирамидыСкачать

Пересечение пирамиды АВСДS прямой а общего положенияСкачать

Начертательная геометрия 1 курс. Построить проекции пирамидыСкачать

Усеченная пирамида (аксонометрия, развертка). Часть 2Скачать








































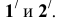

 .
.