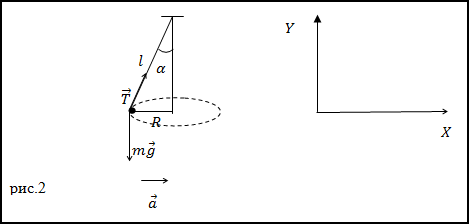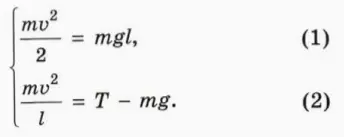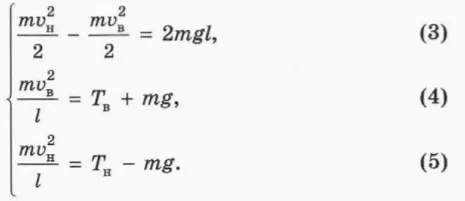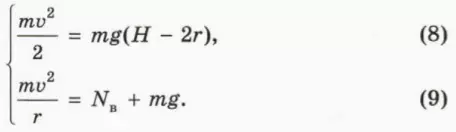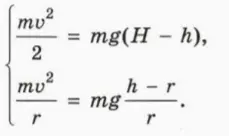- Камень привязан к веревке и движется по окружности в вертикальной плоскости. Одинаковы ли натяжения веревки в верхней и нижней точках?
- Ваш ответ
- решение вопроса
- Похожие вопросы
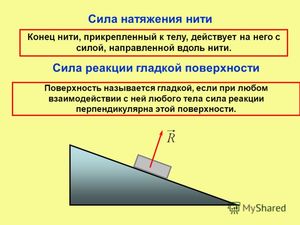
- Сила натяжения нити и применение формулы в бытовых ситуациях
- Натяжения нити и подобных объектов
- 1 Этап
- 2 Этап
- 3 Этап
- 4 Этап
- 5 Этап
- Видео
- Формула силы натяжения нити
- Определение и формула силы натяжения нити
- Единицы измерения силы натяжения нити
- Примеры решения задач
- Неравномерное движение по окружности в вертикальной плоскости
- 1. Груз, подвешенный на нити и стержне
- «Шестикратный вес»
- В какой точке шарик сойдет с окружности?
- Груз, подвешенный на стержне
- 2. Движение по «мертвой петле»
- З. Соскальзывание с полусферы
- Дополнительные вопросы и задания
- Формула силы натяжения нити
- Определение и формула силы натяжения нити
- Единицы измерения силы натяжения нити
- Примеры решения задач
- Видео
Видео:Физика - движение по окружностиСкачать

Камень привязан к веревке и движется по окружности в вертикальной плоскости. Одинаковы ли натяжения веревки в верхней и нижней точках?
Видео:Движение тел по окружностиСкачать

Ваш ответ
Видео:Центростремительное ускорение. 9 класс.Скачать

решение вопроса
Видео:Урок 90. Движение по окружности (ч.2)Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,868
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Сила натяжения нити и применение формулы в бытовых ситуациях
Силой натяжения называют ту, что действует на объект, сравнимый с проволокой, шнуром, кабелем, ниткой и так далее. Это могут быть несколько объектов сразу, в таком случае сила натяжения будет действовать на них и необязательно равномерно. Объектом натяжения называют любой предмет, подвешенный на все вышеперечисленное. Но кому это нужно знать? Несмотря на специфичность информации, она может пригодиться даже в бытовых ситуациях.
Например, при ремонте дома или квартиры. Ну и, конечно же, всем людям, чья профессия связана с расчетами:
- инженерам;
- архитекторам;
- проектировщикам и пр.
Видео:Сила натяжения нити (видео 26) | Силы. Законы Ньютона | ФизикаСкачать

Натяжения нити и подобных объектов
А зачем им это знать и какая от этого практическая польза? В случае с инженерами и конструкторами знания о мощи натяжения позволят создавать устойчивые конструкции. Это означает, что сооружения, техника и прочие конструкции смогут дольше сохранять свою целостность и прочность. Условно, эти расчеты и знания можно разделить на 5 основных пунктов, чтобы в полной мере понять, о чем идет речь.
1 Этап
Задача: определить силу натяжения на каждом из концов нити. Эту ситуацию можно рассматривать как результат воздействия сил на каждый конец нити. Она равняется массе, помноженной на ускорение свободного падения. Предположим, что нить натянута туго. Тогда любые воздействия на объект приведет к изменению натяжения (в самой нити). Но даже при отсутствии активных действий, по умолчанию будет действовать сила притяжения. Итак, подставим формулу: Т=м*g+м*а, где g – ускорение падения (в данном случае подвешенного объекта), а – любое иное ускорение, действующее извне.
Есть множество сторонних факторов, влияющих на расчеты – вес нити, ее кривизна и так далее. Для простых расчетов это мы не будем пока что учитывать. Иными словами – пусть нить будет идеальна с математической точки зрения и «без изъянов».
Возьмем «живой» пример. На балке подвешена прочная нить с грузом в 2 кг. При этом отсутствует ветер, покачивания и прочие факторы, так или иначе влияющие на наши расчеты. Тогда мощь натяжения равна силе тяжести. В формуле это можно выразить так: Fн=Fт=м*g, в нашем случае это 9,8*2=19,6 ньютона.
2 Этап
Заключается он в вопросе об ускорении. К уже имеющейся ситуации давайте добавим условие. Суть его в том, чтобы на нить действовало еще и ускорение. Возьмем пример попроще. Представим, что нашу балку теперь поднимают вверх со скоростью 3 м/с. Тогда, к натяжению прибавится ускорение груза и формула примет следующий вид: Fн=Fт+уск*м. Ориентируясь на прошлые расчеты получаем: Fн=19,6+3*2=25,6 ньютона.
3 Этап
Тут уже посложнее, так как речь идет об угловом вращении. Следует понимать, что при вращении объекта вертикально, сила, воздействующая на нить, будет намного больше в нижней точке. Но давайте возьмем пример с несколько меньшей амплитудой качания (по типу маятника). В этом случае для расчетов нужна формула: Fц=м* v²/r. Тут искомое значение обозначает дополнительную мощь натяжения, v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз. Последнее значение фактически равняется длине нити, пускай она составляет 1,7 метра.
Итак, подставляя значения, находим центробежные данные: Fц=2*9/1,7=10,59 ньютона. А теперь, чтобы узнать полную силу натяжения нити, надо к имеющимся данным о состоянии покоя прибавить центробежную силу: 19,6+10,59=30,19 ньютона.
4 Этап
Следует учитывать меняющуюся силу натяжения по мере прохождения груза через дугу. Иными словами – независимо от постоянной величины притяжения, центробежная (результирующая) сила меняется по мере того, как качается подвешенный груз.
Чтобы лучше понять этот аспект, достаточно представить себе привязанный груз к веревке, которую можно свободно вращать вокруг балки, к которой она закреплена (как качели). Если веревку раскачать достаточно сильно, то в момент нахождения в верхнем положении сила притяжения будет действовать в «обратную» сторону относительно силы натяжения веревки. Иными словами – груз станет «легче», из-за чего ослабнет и натяжение на веревку.
Предположим, что маятник отклоняется на угол, равный двадцати градусам от вертикали и движется со скоростью 1,7 м/с. Сила притяжения (Fп) при этих параметрах будет равна 19,6*cos(20)=19,6*0,94=18,424 Н; центробежная сила (F ц=mv²/r)=2*1,7²/1,7=3,4 Н; ну а полное натяжение (Fпн) будет равняться Fп+ Fц=3,4+18,424=21,824 Н.
5 Этап
Его суть заключается в силе трения между грузом и другим объектом, что в совокупности косвенно влияет на натяжение веревки. Иначе говоря – сила трения способствует увеличению силы натяжения. Это хорошо видно на примере перемещения объектов по шершавой и гладкой поверхностях. В первом случае трение будет большим, поэтому и сдвигать предмет становится тяжелее.
Общее натяжение в данном случае вычисляется по формуле: Fн=Fтр+Fу, где Fтр – трение, а Fу – ускорение. Fтр=мкР, где мк – трение между объектами, а Р – сила взаимодействия между ними.
Чтобы лучше понять данный аспект, рассмотрим задачу. Допустим, у нас груз 2 кг и коэффициент трения равен 0,7 с ускорением движения 4м/с постоянной скорости. Теперь задействуем все формулы и получаем:
- Сила взаимодействия — Р=2*9,8=19,6 ньютона.
- Трение — Fтр=0,7*19,6=13,72 Н.
- Ускорение — Fу=2*4=8 Н.
- Общая сила натяжения — Fн=Fтр+Fу=13,72+8=21,72 ньютона.
Теперь вы знаете больше и можете сами находить и рассчитывать нужные значения. Конечно, для более точных расчетов нужно учитывать больше факторов, но для сдачи курсовой и реферата этих данных вполне достаточно.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Видео
Это видео поможет вам лучше разобраться в данной теме и запомнить ее.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Формула силы натяжения нити
Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Определение и формула силы натяжения нити
Силу натяжения определяют как равнодействующую сил $(bar )$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar $ и $bar $, и $bar $ . Математически определение для силы натяжения нити можно записать как:
где $bar $ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Видео:Физика 10 класс : Динамика движения по окружностиСкачать

Примеры решения задач
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
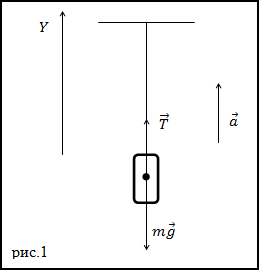
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
где $bar $ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
Ответ. a=1,2м/с 2
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Из рис.2 видно, что:
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
Видео:Физика | Равномерное движение по окружностиСкачать

Неравномерное движение по окружности в вертикальной плоскости
1. Груз, подвешенный на нити и стержне
Шарик массой m подвешен в точке O на нити длиной l (рис. 33.1). Отведем его на угол 90′ и отпустим без толчка. Шарик начнет двигаться по окружности.
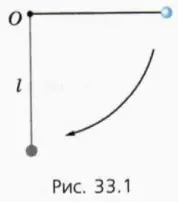
Обозначим 
? 1. Используя рисунок 33.2, ответьте на вопросы:
а) Какие силы показаны на рисунке?
б) Как направлено ускорение шарика?
в) Выразите модуль равнодействующей через модули показанных сил.
? 2. Перенесите в тетрадь рисунок 33.2, укажите на нем ускорение шарика и объясните смысл следующих уравнений:
? 3. Шарик массой 100 г подвешен на нити длиной 1 м. Его отклоняют на 90º и отпускают без толчка.
а) Чему равна сила натяжения нити, когда шарик проходит положение равновесия?
б) Во сколько раз вес шарика при прохождении положения равновесия больше силы тяжести?
Подсказка. Чтобы найти силу натяжения нити, удобно разделить уравнение (2) иа уравнение (1). Вспомните определение веса тела.
Итак, в данном случае при прохождении шариком положения равновесия нить должна выдержать «тройной вес»!
Сообщим шарику в нижней точке такую скорость 
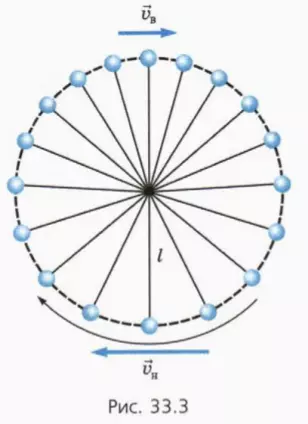
На рисунке показаны последовательные положения шарика через равные промежутки времени (их можно зафиксировать, например, с помощью видеосъемки).
? 4. Почему в верхней части рисунка расстояния между последовательными положениями шарика меньше?
? 5. Сделайте в тетради чертеж, на котором изобразите:
а) силы, действующие на шарик в верхней и нижней точках окружности (обозначьте 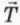
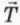
б) ускорение шарика в этих точках. В верхней точке ускорение направлено вниз, а в нижней – вверх.
? 6. Объясните смысл следующих уравнений:
? 7. Подвешенный на нити шарик массой 100 г вращается в вертикальной плоскости. Насколько больше сила натяжения нити, когда шарик проходит положение равновесия, чем когда он находится в верхней точке окружности?
Подсказка. Удобно вычесть уравнение (4) из уравнения (б) и сравнить полученное уравнение с уравнением (3).
«Шестикратный вес»
Шарик движется но окружности при условии, что нить натянута. Поэтому минимальная скорость, которую нужно сообщить шарику в нижней точке, чтобы он стал двигаться по окружности„должна быть такой, чтобы сила натяжения нити обратилась в нуль только в верхней точке окружности.
? 8. Шарику, подвешенному на нити длиной l, сообщили в нижней точке минимальную горизонтальную скорость, необходимую для того, чтобы он начал двигаться по окружности. Сделайте чертеж, на котором изобразите силы, действующие на шарик в верхней и нижней точках окружности. Чему в этом случае равны:
а) скорость шарика в верхней точке окружности?
б) ускорение шарика в верхней точке окружности?
в) скорость шарика в нижней точке окружности?
г) вес шарика в нижней точке окружности?
Подсказка. Воспользуйтесь уравнениями (3)–(5).
Итак, когда груз проходит нижнюю точку, нить должна выдерживать шестикратный вес груза!
В какой точке шарик сойдет с окружности?
Пусть теперь скорость шарика в нижней точке недостаточна для того, чтобы он мог совершить полный оборот.
В таком случае есть две возможности.
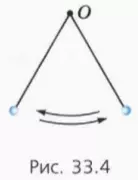
1) Шарик не поднимется выше точки подвеса О. Тогда он начнет колебаться между крайними положениями (рис. 33.4).
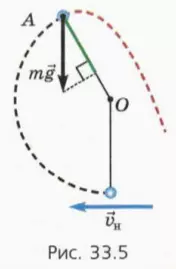
2) Шарик поднимется выше точки подвеса, но сила натяжения нити обратится в некоторой точке А в нуль (рис. 33.5). После этого шарик будет двигаться по параболе, показанной красным пунктиром. Когда шарик находится в точке А, центростремительное ускорение ему сообщает только составляющая силы тяжести, направленная вдоль радиуса к центру окружности. На рисунке показано, как найти модуль этой составляющей (отрезок зеленого цвета).
? 9. Шарику массой m, подвешенному на нити длиной l, сообщают горизонтальную начальную скорость v0. Когда шарик находится на высоте h, сила натяжения нити обращается в нуль. Обозначим скорость шарика в этот момент. Используя рисунок 33.6:
а) объясните смысл уравнений
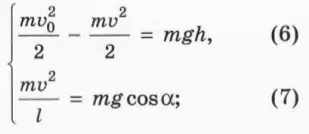
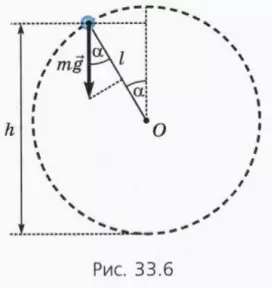
б) выразите h через l и альфа.
? 10. Шарику массой 200 г, подвешенному на нити длиной 50 см, сообщают горизонтальную скорость 4 м/с.
а) До какой высоты (по отношению к положению равновесия) шарик будет двигаться по окружности?
б) Чему будет равна сила натяжения нити, когда шарик будет находиться на одной горизонтали с точкой подвеса?
Подсказка. Когда шарик находится на одной горизонтали с точкой подвеса, центростремительное ускорение шарику сообщает только сила натяжения нити.
? 11. Небольшая шайба массой m лежит внутри закрепленного цилиндра. Ось цилиндра горизонтальна (рис. 33.7). Внутренний радиус цилиндра 30 см, стенки цилиндра гладкие. Какую скорость v0 надо сообщить шайбе перпендикулярно оси цилиндра, чтобы она:
а) совершила полный оборот, двигаясь по окружности?
б) оторвалась от поверхности цилиндра на высоте 40 см?
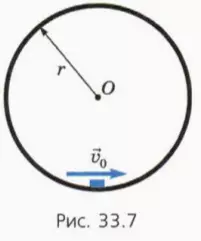
Подсказки. Движение шайбы в цилиндре отличается от движения подвешенного на нити шарика только тем, что роль силы натяжения нити играет сила нормальной реакции, а длину нити l надо заменить на радиус цилиндра r.
Груз, подвешенный на стержне
Рассмотрим теперь вращение груза, подвешенного на легком стержне (массой стержня можно пренебречь). В отличие от нити стержень сохраняет форму и поэтому не дает грузу сойти с окружности. По этой причине минимально возможная скорость груза в верхней точке равна нулю.
? 12. Шарик подвешен на легком стержне длиной l, который может вращаться без трения вокруг точки подвеса O.
а) Какова минимально возможная скорость шарика в верхней точке траектории?
б) Какую минимальную скорость надо сообщить шарику в нижней точке, чтобы он совершил полный оборот?
в) Чему равен вес шарика в нижней точке?
Итак, подвешенному на стержне шарику надо сообщить меньшую начальную скорость, чтобы он сделал полный оборот, чем в случае, когда шарик подвешен на нити той же длины.
2. Движение по «мертвой петле»
Рассмотрим движение тела в вертикальной плоскости по гладкому желобу, переходящему в окружность (рис. 33.8). По аналогии с фигурой высшего пилотажа, когда самолет совершает круговой виток в вертикальной плоскости, такое движение называют иногда мертвой петлей.
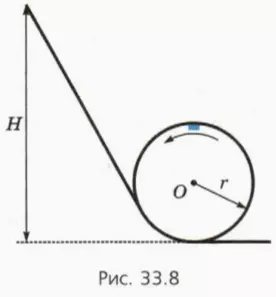
Движение по круговому желобу очень похоже на рассмотренное выше движение подвешенного на нити груза. Роль действующей на груз силы натяжения нити 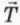

? 13. Небольшая шайба массой m соскальзывает с высоты H по гладкому наклонному желобу, переходящему в окружность радиусом r, и движется по окружности, не отрываясь от желоба. Обозначим 
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в верхней и нижней точках окружности.
б) Объясните смысл следующих уравнений:
? 14. Чему равна минимальная высота Hmin, с которой должна соскальзывать шайба, чтобы она могла совершить полный оборот?
Подсказка. В этом случае Nв обращается в нуль в верхней точке окружности.
Если начальная высота шайбы H меньше, чем Hmin, то в некоторой точке шайба оторвется от желоба. В этой точке сила нормальной реакции обращается в нуль.
? 15. Небольшая шайба массой m соскальзывает с высоты H по гладкому желобу, переходящему в окружность радиусом r, и отрывается от желоба на высоте h (по отношению к нижней точке окружности). Скорость шайбы в этот момент обозначим v.
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от желоба.
б) Используя этот чертеж, объясните смысл уравнений
? 16. Небольшая шайба массой 50 г соскальзывает с некоторой высоты H по гладкому желобу, переходящему в окружность радиусом 30 см, и отрывается от желоба на высоте 40 см (по отношению к нижней точке окружности).
а) Чему равно H?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?
З. Соскальзывание с полусферы
Пусть на вершине гладкой полусферы радиусом г, укрепленной на столе, лежит небольшая шайба массой m (рис. ЗЗ.9). От незначительного толчка шайба начинает соскальзывать.

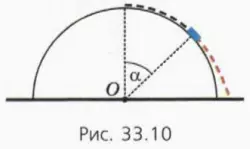
Пока шайба скользит, действующая на нее сила нормальной реакции уменьшается. В некоторой точке она обратится в нуль – в этот момент шайба оторвется от полусферы (рис. 33.10) и начнет двигаться по параболе (красная пунктирная линия). Обозначим и скорость шайбы в момент отрыва от полусферы.
? 17. Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы, и направление скорости шайбы в этот момент. Обозначьте h высоту, на которой находится при этом шайба, а α – угол между радиусом, проведенный к шайбе и вертикалью. Используя этот чертеж:
а) объясните смысл уравнений

б) выразите h через r и α.
в) выразите h через r.
? 18. На вершине гладкой сферы лежит небольшая шайба массой m, соединенная нитью с грузом массой M (рис. 33.11). В начальный момент тела покоятся. Их отпускают без толчка. Шайба отрывается от полусферы, когда угол между радиусом, проведенным к шайбе, и вертикалью равен α. Обозначим и модуль скорости тел в момент отрыва.

а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы.
Подсказка. В момент отрыва на шайбу действуют только сила тяжести и сила натяжения нити, направленная по касательной к окружности.
б) Насколько опустилась шайба и насколько опустился груз к моменту отрыва шайбы по сравнению с их начальным положением?
Подсказка. См. рисунок 33.12. Шайба опустилась на расстояние, отмеченное синим отрезком, а груз опустился на расстояние (зеленый отрезок), равное длине дуги, пройденной шайбой до отрыва (зеленый пунктир). Длина дуги равна rα (где α задано в радианах).
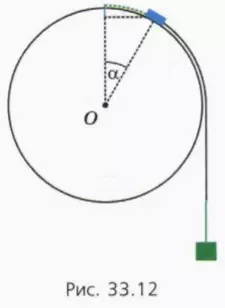
в) Используя этот чертеж, объясните смысл уравнений
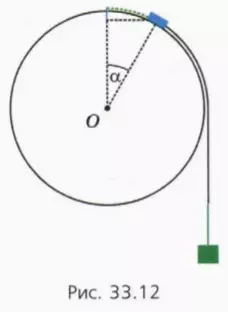
Подсказка. Действующая на шайбу сила натяжения нити направлена по касательной к окружности. Поэтому центростремительное ускорение шайбе перед самым отрывом сообщает только составляющая действующей на шайбу силы тяжести, направленная по радиусу к центру окружности.
г) Чему равно отношение M/m, если α = π/6?
Дополнительные вопросы и задания
19. Какую скорость можно сообщить шарику в нижней точке, чтобы он начал совершать колебания, если:
а) шарик подвешен на нити длиной l?
б) шарик подвешен на легком стрежне длиной l?
Подсказка. Шарик на нити не должен подняться выше точки подвеса, а шарик на стержне не должен достичь верхней точки окружности.
20. Небольшая шайба массой m соскальзывает с высоты H = 2r по гладкому желобу, переходящему в окружность с радиусом r.
а) На какой высоте h (по отношению к нижней точке окружности) шайба оторвется от желоба?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?
21. На гладкой полусфере радиуса r, укрепленной на столе, лежит небольшая шайба. Ей сообщают начальную горизонтальную скорость v0. На какой высоте h от стола шайба оторвется от полусферы?
Подсказка. Если начальная скорость достаточно велика, шайба оторвется от полусферы сразу.
22. На укрепленной на столе полусфере радиуса r лежит небольшая шайба массой m. От незначительного толчка шайба начинает соскальзывать. Вследствие трения за время, в течение которого шайба скользила по полусфере, выделилось количество теплоты Q.
а) На какой высоте h шайба оторвалась от полусферы?
б) На какой высоте h шайба оторвалась от полусферы, если выделившееся количество теплоты равно кинетической энергии шайбы в момент отрыва?
23. Впервые в мире круговой виток в вертикальной плоскости выполнил русский летчик П. Н. Нестеров в 1913 году. Эту фигуру высшего пилотажа называют мертвой петлей или петлей Нестерова. Нестеров так доверял своим расчетам, что перед выполнением мертвой петли не пристегнулся ремнями к креслу пилота. Расчет летчика оказался правильным: ремни не понадобились! Почему при выполнении мертвой петли летчик не выпадает из кресла пилота в верхней точке траектории?
Видео:Неравномерное движение по окружности в вертикальной плоскостиСкачать
Формула силы натяжения нити
Видео:Урок 89. Движение по окружности (ч.1)Скачать

Определение и формула силы натяжения нити
Силу натяжения определяют как равнодействующую сил $(bar)$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar$ и $bar$, и $bar$ . Математически определение для силы натяжения нити можно записать как:
где $bar$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Видео:Введение в силу натяжения нити. Часть 1 (видео 23) | Силы. Законы Ньютона | ФизикаСкачать

Примеры решения задач
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
где $bar$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
Ответ. a=1,2м/с 2
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$ begin X: quad T sin alpha=m a=m omega^ R(2.2) \ Y: quad-m g+T cos alpha=0 end $$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Из рис.2 видно, что:
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
📺 Видео
УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Мгновенный центр вращенияСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Задача на вертикально вращающееся йо-йо(видео 10)| Центростремительная силаСкачать