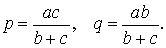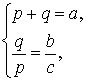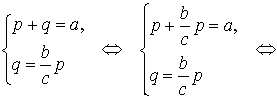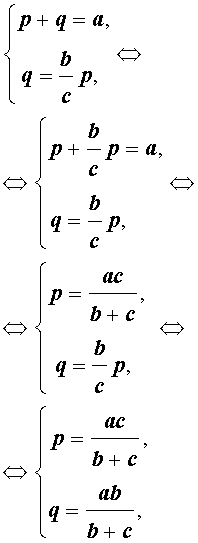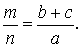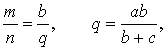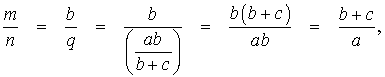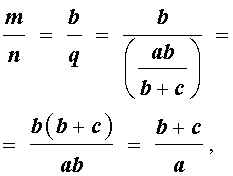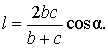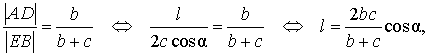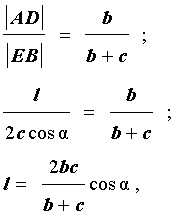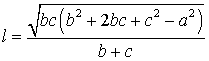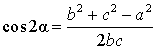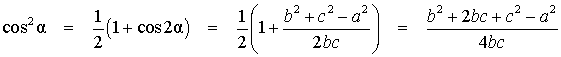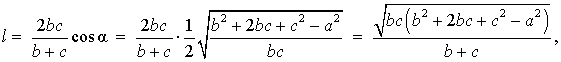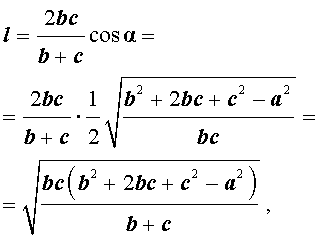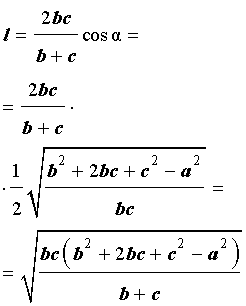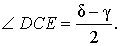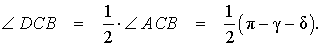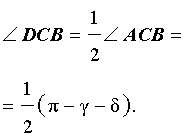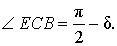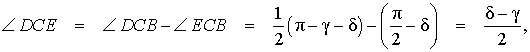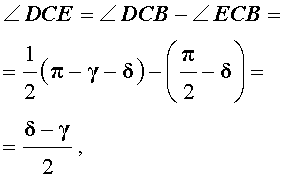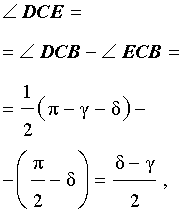Напомним, что биссектрисой угла называют луч, делящий угол пополам.
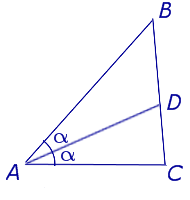
Определение . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).
Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.
На рисунке 1 биссектрисой является отрезок AD .
Теорема 1 . Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
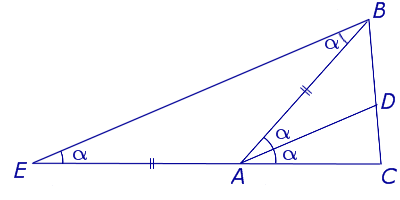
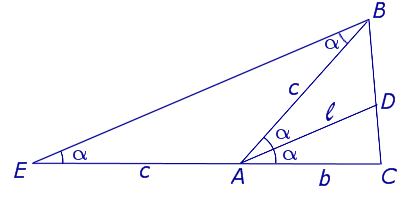
Доказательство . Продолжим сторону AC треугольника ABC , изображенного на рисунке 1, за точку A . Проведем через точку B прямую, параллельную биссектрисе AD . Обозначим точку пересечения построенных прямых буквой E (рис. 2).
Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD , поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD . Заметим также, что угол BEA равен углу DAC , поскольку эти углы являются соответственными при параллельных прямых EB и AD . Таким образом, угол EBA равен углу BEA , откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.
Отсюда, воспользовавшись теоремой Фалеса, получаем:
что и требовалось доказать.
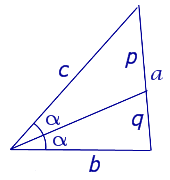
Следствие 1 . Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения
b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.
что и требовалось доказать.
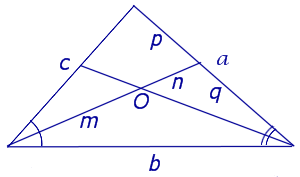
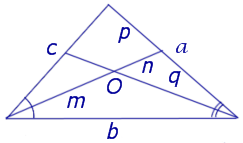
Следствие 2 . Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O .
Тогда справедлива формула:
что и требовалось доказать.
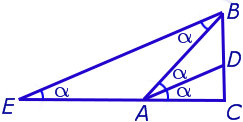
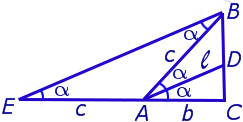
Теорема 2 . Рассмотрим рисунок 5, который практически совпадает с рисунком 2.
Тогда для длины биссектрисы справедлива формула:
Доказательство . Из рисунка 5 следует формула
Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC , получаем:
что и требовалось доказать.
Теорема 3 . Длину биссектрисы треугольника (рис.6) можно найти по формуле:
Доказательство . Рассмотрим рисунок 6
откуда с помощью Теоремы 2 получаем:
что и требовалось доказать.
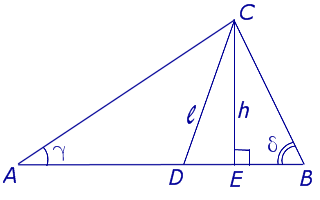
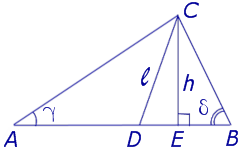
Задача . Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высота CE .
Доказать, что выполнено равенство:
Решение . Поскольку CD – биссектриса угла ACB , то
Поскольку CE – высота, то
что и требовалось доказать.
Из решения этой задачи вытекает простое следствие.
Следствие . Длины биссектрисы CD и высоты CE связаны следующей формулой:
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Построение треугольника по трем биссектрисам
Задача о построении треугольника по заданным биссектрисам. По существу, классическими задачами на построение являются также и задачи, связанные с построением треугольника.
Легко построить треугольник по трем сторонам, чуть сложнее сделать это, если даны три его медианы или три высоты. Самый трудный случай возникает для трех данных биссектрис.
Эта задача трудна даже для равнобедренного треугольника, т.е. тогда, когда две биссектрисы совпадают (если равны все три биссектрисы, то задача легко решается).
АЕ, BD — биссектрисы треугольника
Пусть в равнобедренном треугольнике АВС известны длины биссектрис АЕ и BD АЕ =а, BD = Ь.
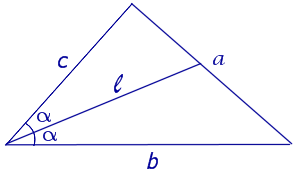
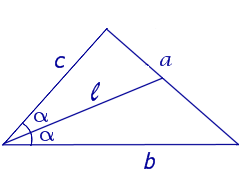
Угол при основании треугольника обозначим а. Треугольник АВС будет построен, как только будет найдено значение какой-либо тригонометрической функции угла а. Пусть sin а = х. Наша цель показать, что не для каждого треугольника отрезок х можно построить с помощью циркуля и линейки.
Найдем площадь треугольника АВС двумя способами:
Хдавс = S MCE + аве =-a-2b- ctg 2а • sin 2а + — ? а • sin а • . .
1 Фердинанд Карл Луис Линдеманн (1852-1939) — немецкий математик, профессор Кенигсбергского (с 1883 г.) и Мюнхенского (с 1893 г.) университетов.
Отсюда получаем уравнение:
sin 2a a sin 2a sin 2a
Пусть — = k; разделив обе части уравнения на (явно ненулевое) число ——,
получим уравнение с параметром к:
2 ? cos 2a • к — cos 2a • sin a + sina.
2(l-2sin 2 a)^ = (1-2sin 2 a)sin a + sin a.
При нашем обозначении x = sin a получаем:
2Л( 1 — 2x 2 ) = 2x( 1 — 2x 2 ) + x,
4x 3 — 4Ax 2 -3x + 2k.
При к = 3 получаем:
4у 3 — 12у 2 -3у + 6.
Простым перебором вариантов можно убедиться, что у этого многочлена нет рациональных корней. По теореме Вантцеля его корни нельзя выразить в квадратных радикалах через коэффициенты уравнения, а это значит, что равнобедренный треугольник с соотношением биссектрис 3 : 1 построить с помощью циркуля и линейки нельзя.
При соотношении биссектрис 1 : 3 многочлен:
12у 3 -4у 2 -9у + 2
также не имеет рациональных корней. Его тоже, используя только циркуль и линейку, построить нельзя.
Задача о построении треугольника по трем биссектрисам с помощью циркуля и линейки в общем случае неразрешима.
Отметим, что невозможность построения связана с ограничением на инструменты. Все три основные задачи древности неразрешимы, если использовать инструменты богов: циркуль и линейку без делений. Но стоит лишь чуть приземлить инструментарий, а именно нанести на линейку всего одно деление, как ситуация меняется.
С помощью циркуля и линейки с делением можно и куб удвоить, и трисектрису построить, и начертить правильный семиугольник.
Рассмотрим для примера построение трисектрисы.
Сначала отметим, что прямой угол делится на три части с помощью циркуля и обычной, «божественной» линейки без делений. Тупой угол можно представить в виде суммы прямого и острого угла. Разделив этот острый угол на три части и прибавим к нему треть прямого (угол в 30°), мы получим одну третью исходного тупого угла. Таким образом, достаточно научиться строить трисектрису лишь острых углов.
Итак, пусть дан острый угол АОВ = а, и нам нужно разделить его на три равные части. В нашем распоряжении есть линейка с делением; допустим, что расстояние от начала линейки до деления равно а. Построим прямую ОВ, а затем проведем полуокружность с центром в точке О и радиусом, равным а. С помощью линейки с делением через точку А проведем прямую так, чтобы отрезок DE, отсеченный полуокружностью и прямой ОВ, был равен а. Через точку О построим луч ОС, параллельный прямой AD.
Луч ОС — это и есть искомая трисектриса угла АОВ.
Для доказательства соединим точки А и Е с центром О нашей окружности и рассмотрим два треугольника: ODE и ОЕА. Оба треугольника равнобедренные, причем угол при основании треугольника ОЕА в два раза больше угла при основании треугольника ODE.
Видео:Построение биссектрисы в треугольникеСкачать

Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Видео:Построение биссектрисы углаСкачать

Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Видео:ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
📹 Видео
Высота, биссектриса, медиана. 7 класс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Угол между двумя биссектрисами треугольникаСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Формула для биссектрисы треугольникаСкачать

Прямоугольный треугольник. Часть 3. Биссектриса | Борис Трушин #shortsСкачать

Биссектрисы треугольника.Скачать

Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать
Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Построение медианы в треугольникеСкачать

Задание 9 ОГЭ от ФИПИСкачать

ОГЭ 16🔴Скачать