Продолжение сторон аб и сд четырехугольника авсд вписанного в окружность пересекаются в точке р

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.

Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.

Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.

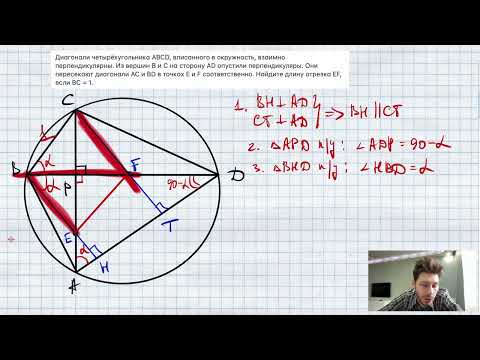
Видео:Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать

Продолжения сторон ab и cd четырехугольника abcd вписанного в окружность пересекаются в точке p?

Геометрия | 5 — 9 классы

Продолжения сторон ab и cd четырехугольника abcd вписанного в окружность пересекаются в точке p.

Градусная мера меньшей дуги окружности, стягиваемой хордой bc равно 30, а градусная мера большей дуги, стягиваемой хордой ad, равно 120.

Найдите градусную меру угла apd.

Нарисовав рисунок , нужно провести прямые АС и DB .

Становится очевидно, что угол DBA = 1 / 2 * 120 = 60 как вписанный .

Аналогично и с углом BDC, который соответственно равен 15

следовательно угол DBP , как смежный с углом DBA, равен 180 — 60 = 120

рассматривая треугольник DBP , очевидно , что искомый угол равен 45

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60 градусам?

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60 градусам.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

В окружности длиной 24π м проведена хорда, равная 12м?

В окружности длиной 24π м проведена хорда, равная 12м.

Найдите градусную меру меньшей дуги, стягиваемой хордой.

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей её хордой, если длина хорды равна 6м, а градусная мера дуги равна 120?

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей её хордой, если длина хорды равна 6м, а градусная мера дуги равна 120.

Видео:Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать

Через точку А окружности проведены диаметр АС и две хорды АB и АD равные радиусу этой окружности?

Через точку А окружности проведены диаметр АС и две хорды АB и АD равные радиусу этой окружности.

Найдите углы четырехугольника ABCD и градусные меры дуг AB BC AD CD.

Видео:Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжениеСкачать

Через точку А окружности проведены диаметр АС и две хорды AB и AD равные радиусу этой окружности?

Через точку А окружности проведены диаметр АС и две хорды AB и AD равные радиусу этой окружности.

Найдите углы четырехугольника ABCD и градусные меры дуг AB, BC, CD, AD.

Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей её хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60 градусов?

Найдите площадь фигуры, ограниченной дугой окружности и стягивающей её хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60 градусов.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Найдите площадь фигуры , ограниченной дугой окружности и стягивающей ее хордой , если длина хорды равна 4 м , а градусная мера дуги равна 60 градусов?

Найдите площадь фигуры , ограниченной дугой окружности и стягивающей ее хордой , если длина хорды равна 4 м , а градусная мера дуги равна 60 градусов.

Решите, пожалуйста, подробно!

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности?

Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности.

Найдите углы четырехугольника ABCD и градусные меры дуг AB, BC, CD, AD.

Видео:ОГЭ 2 часть|Биссектрисы углов A и B трапеции/параллелограмма ABCD пересекаются в точке F. Найдите ABСкачать

Длина дуги окружности 3 пи / 4 см?

Длина дуги окружности 3 пи / 4 см.

Найти длину хорды, стягивающей эту дугу, если градусная мера дуги 120.

Видео:2128 в четырёхугольник ABCD вписана окружность AB = 7 BC = 12 CD = 9Скачать

В окружности длиной 24пи проведена хорда, равная 12 см?

В окружности длиной 24пи проведена хорда, равная 12 см.

Найти градусную меру меньшей дуги, стягиваемой хордой.

Вопрос Продолжения сторон ab и cd четырехугольника abcd вписанного в окружность пересекаются в точке p?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Высота равностороннего треугольника через его сторону : h = a√3 / 2, где а — сторона треугольника⇒ а = 2h / √3 = 2 * 9 * √3 / √3 = 18.

А — гипотенуза (и она жесторона равностороннеготреугольника) а / 2 — катет (половина основания равностороннего треугольника) h — катет (высотаравностороннего треугольника) По теореме Пифагора а² = (a / 2)² + h² a² — a² / 4 = h² 3 / 4 * a² = h² a² = 4..

90 градусов так как смежные углы дают в сумме 180 градусов.

Треугольник ABC — прямоугольный, гипотенуза AB = 10, катет AC = 8, тогда второй катет по теореме Пифагора BC² = AB² — AC² = 100 — 64 = 36 BC = 6.

При пересечении 2 — х прямых образуются 2 пары равных между собой углов. Называемых вертикальными. Если один из них 29 . Есть еще один такой же. А величину каждого из второй пары найдите вычитанием из 180 — ти 29 — ти.

180 — 91° — 72° = 17° ADC 17°.

Этот треугольник может быть равносторонним и равнобедренным.

Видео:Четырёхугольник ABCD вписан в окружность причём BC CD Известно что угол ADC равен 93Скачать

Продолжения сторон AB и CD вписанного четырёхугольника ABCD пересекаются в точке P, а продолжения BC и AD — в точке Q. Докажите, что точки пересечения биссектрис углов AQB и BPC со сторонами четырёхугольника являются вершинами ромба.

Пусть P₁ и P₂ — точки пересечения биссектрисы угла BPC с окружностью, описанной около четырёхугольника ABCD, а Q₁ и Q₂ — биссектрисы угла AQB, причём точка P₁ лежит между P и P₂, Q₁ — между Q и Q₂. Тогда

AP₂ — BP₁ = DP₂ — CP₁, DQ₂ — AQ₁ = CQ₂ — BQ₁,

AP₂ + CP₁ = DP₂ + BP₁, AQ₁ + CQ₂ = DQ₂ + BQ₁.

Сложив почленно эти два равенства, получим, что

AP₂ + AQ₁ + CP₁ + CQ₂ = DP₂ + DQ₂ + BP₁ + BQ₁ = 180 o .

Если K — точка пересечения указанных биссектрис, то

PKQ = P₁KQ₁ = ( AP₂ + AQ₁ + CP₁ + CQ₂) = 90 o .

Если M и N — точки пересечения прямой Q₁Q₂ со сторонами AB и CD, то треугольник PMN — равнобедренный, т.к. его биссектриса PK является высотой. Поэтому MK = KN. Аналогично докажем, что K — середина второй диагонали полученного четырёхугольника. Следовательно, это ромб.

💥 Видео

ОГЭ по математике. Задача 25-2Скачать

#26. EGMO-2022, Problem 6Скачать

#29. Регион ВсОШ 2023, 9.5Скачать

№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Решение задачи 25 из ОГЭ по математике 9 классСкачать

Решение задания №16 варианта 1 из ОГЭ по математике Ященко 36 вариантов ФИПИ 2023 Ответы ГДЗСкачать

ОГЭ 2020 задание 18Скачать

Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать