Поток вектора плотности тока (4 видео) | Курс школьной геометрии

Электрический ток и его плотность

Электрическим током называют направленное движение свободно заряженных частиц под действием электрического поля.

Как правило движение зарядов происходит в некоторой среде (веществе или вакууме), являющейся проводником для электрического тока. Движущимися в среде заряженными частицами могут быть электроны (в металлах, полупроводниках) или ионы (в жидкостях и газах).

Рис. 1 Электрический ток

Для возникновения и протекания электрического тока в любой токопроводящей среде необходимо выполнение двух условий:

Наличие в среде свободных носителей заряда;
Наличие электрического поля.

Для поддержания электрического поля, например в проводнике, к его концам необходимо подключить какой-либо источник электрической энергии (батарейку или аккумулятор). Поле в проводнике создается зарядами, которые накопились на электродах источника тока под действием сил (химических, механических и т.д.).

За направление тока условно принято принимать направление движения положительных зарядов. Следовательно, условно принятое направление тока обратно направлению движения электронов – основных отрицательных электрических носителей заряда в металлах и полупроводниках.

Понять явление электрического тока достаточно сложно так как его невозможно увидеть глазами. Для лучшего понимания процессов в электронике проведем аналогию между электрическим током в проводнике и водой в тонкой трубочке. В трубочке есть вода (носители заряда в проводнике), но она неподвижна, если трубочка лежит на горизонтальной поверхности и уровень высот ее концов (значения потенциалов электрического поля) одинаковый. Если трубочку наклонить так, что один конец станет выше другого (появится разность потенциалов), вода потечет по трубочке (электроны придут в движение).

Способность вещества проводить электрический ток под действием электрического поля называется электропроводностью. Каждому веществу соответствует определенная степень электропроводности. Ее значение зависит от концентрации в веществе носителей заряда – чем она выше, тем больше электропроводность. В зависимости от электропроводности все вещества делятся на три большие группы: проводники, полупроводники и диэлектрики.

Электрический ток может менять направление и величину во времени (переменный ток) или оставаться неизменным (постоянный) (рисунок 2).

Рис. 2. Постоянный и переменный электрические токи

Количественной мерой электрического тока служит сила тока I, которая определяется числом электронов (зарядов) q, проходящих через импровизированное поперечное сечение проводника в единицу времени t (рисунок 3).

Рис. 3. Сила тока в проводнике

Для постоянного тока представленное выше выражение можно записать в виде

Ток в системе СИ измеряется в амперах, [А]. Току в 1 А соответствует ток, при котором через поперечное сечение за 1 секунду проходит электрический заряд, равный 1 Кл.

Содержание

Плотность электрического тока
Сила тока — поток плотности тока
Сила и плотность тока. Линии тока
Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью
🌟 Видео

Плотность электрического тока

Под плотностью тока j понимается физическая величина, равная отношению тока I к площади поперечного сечения S проводника. При равномерном распределении тока по поперечному сечению проводника.

J = I/S

Плотность тока в системе СИ измеряется в амперах на миллиметр квадратный, [А/мм 2 ].

Рассмотрим плотность тока в проводнике с разным поперечным сечением. Например, соединены два проводника с различными сечениями: первый толстый провод с большим поперечным сечением S1 второй тонкий провод с сечением S2. К концам которых приложено постоянное напряжение (рисунок 5) в следствии чего через них протекает постоянный ток с одинаковой силой тока.

Рис.5 Плотность тока в проводниках с различными сечениями.

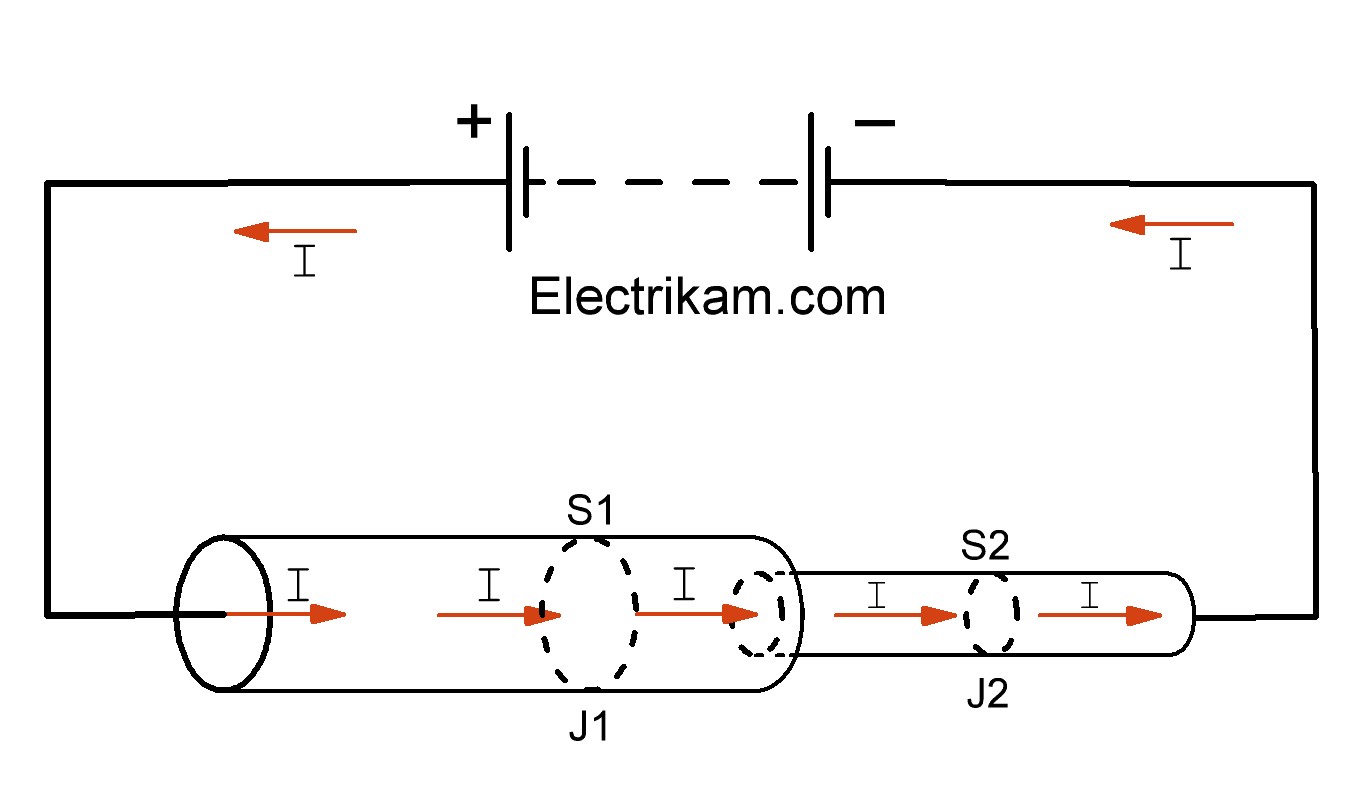
Предположим, что сила тока через поперечное сечение толстого проводника S1 и тонкого провода S2 различная. Из этого предположения вытекает, что за каждую единицу времени через сечения S1 и S2 протекают различные значения электрического заряда. Следовательно, в объёме провода, расположенного между двумя указанными сечениям происходит непрерывное скапливание зарядов, и напряженность электрического поля изменялась бы, чего не может быть, так как при изменении электрического поля ток был бы непостоянен. В проводах с различным сечением при одном и том же токе плотность тока обратно пропорциональна площади поперечного сечения.

Плотность тока — векторная величина.

Рис. 4. Графическая интерпретация плотности тока j

Направление вектора совпадает с направлением положительно заряженных зарядов и, следовательно, с направлением самого тока I.

Если концентрация носителей тока равна n, каждый носитель имеет заряд e и скорость его движения в проводнике равна v (рисунок 3), то за время dt через поперечное сечение S проводника переносится заряд

В этом случае величину силы тока I можно представить в виде зависимости

а плотность тока

Сила тока через произвольную поверхность определяется через поток вектора плотности тока, как интеграл по произвольной (в общем случае) поверхности S (рисунок 6)

Рис. 6. Сила тока через произвольную поверхность S

От величины плотности тока зависит важный показатель – качество электропередачи. Фактически этот показатель зависит от степени нагрузки проводника (хотя и не только от нее). В зависимости от значения плотности тока принято выбирать сечение проводов – это связано с наличием у проводников сопротивления, в результате которого происходит нагрев жил проводника вплоть до его расплавления и выхода из строя.

Видео:Сила тока плотность токаСкачать

Сила тока — поток плотности тока

Рассмотрим теперь общий случай упорядоченного движения заряженных частиц в проводящей среде. Носители тока являются микроскопическими частицами, совершающими беспорядочное тепловое движение. При этом каждая частица в данное мгновение имеет свою скорость. Пусть в некотором физически бесконечно малом объеме dV проводника содержится dN носителей тока. Средней скоростью упорядоченного движения этих частиц называется вектор и, определяемый формулой

где Vi — скорость одной из частиц, содержащихся в объеме dV. i — номер частицы. Вектор и можно определить таким образом для любой точки пространства внутри проводника, т.е. объем dV можно расположить в любом месте проводника. Иначе говоря, вектор средней скорости есть функция точки пространства. Кроме этого, средняя скорость может изменяться со временем: и = и(*, г). Когда частицы движутся совершенно беспорядочно, их средняя скорость равна нулю. Если же заряженные частицы движутся преимущественно в одном направлении, то и ф 0, т.е. по проводнику идет электрический ток.

Плотностью электрического тока называют вектор

где qi — заряд частицы под номером i, заключенной в объеме dV. Плотность тока в различных малых объемах dV проводника может принимать различные значения и может изменяться с течением времени:

В том случае, когда все носители тока имеют одинаковые заряды: qi = Я, формула (4.32) принимает вид

— концентрация носителей тока. Объемная плотность д свободных зарядов связана с концентрацией носителей тока соотношением

Поэтому формулу (4.34) можно записать так:

Пусть в пространстве, заполненном проводящей средой, по которой течет электрический ток, задано векторное поле j = j(t, г), описывающее этот ток. Линиями тока называются линии, касательные к которым в каждой точке пространства совпадают но направлению с вектором плотности тока. Построим внутри проводника с током произвольный замкнутый контур С. Проведем через каждую точку этого контура линию тока. Образованная этими линиями поверхность называется трубкой линий тока, а объем внутри этой поверхности — трубкой тока (рис. 4.8).

Рис. 4.8. Линии тока и трубка тока „ _а ^ ЧС ‘

К определению силы тока

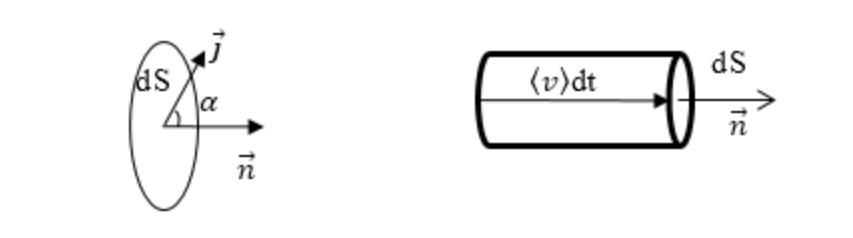
Произведем сечение ’’узкой” трубки тока некоторой поверхностью S (рис. 4.9). Пусть dS есть площадь сечения, а п — единичный вектор, перпендикулярный к поверхности 5. Выясним физический смысл потока вектора плотности тока через элемент поверхности

где dS = ndS — векторный элемент поверхности S. При помощи формулы (4.35) это равенство можно записать так:

где в — угол между вектором плотности тока и нормалью к поверхности, dt — произвольный интервал времени. Построим еще одно сечение dS₀ трубки тока, которое находится на расстоянии и dt от сечения dS. Объем части трубки тока между этими сечениями, т.е. объем цилиндра, равен и dt cos в dS. Предположим, что электрический ток создается движением положительных зарядов. Эти заряды сначала протекают через сечение dS_0> а затем — через dS. Произведение и dt есть среднее расстояние, которое преодолевает носитель тока за время dt_> двигаясь вдоль линии тока. Поэтому все носители тока, которые имелись внутри трубки тока между сечениями dS₀ и dS в некоторый момент времени, спустя время dt окажутся за сечением dS. При этом они перенесут через сечение dS свой электрический заряд, который равен произведению плотности заряда д на объем той части трубки тока, где находились эти частицы. Таким образом, выражение (4.37) есть электрический заряд dQ, протекающий за время dt через элемент поверхности площадью dS:

Отношение заряда, протекающего через некоторую поверхность, ко времени протекания есть сила тока. Согласно этому определению величина dl в формулах (4.36) и (4.37) есть сила тока, протекающего через элемент поверхности dS:

Заряд, протекающий за некоторое время через поверхность 5, равен сумме зарядов, протекающих за это время через различные элементы поверхности. Поэтому сила тока /, протекающего через поверхность 5, будет равна сумме сил токов dl через элементы этой поверхности, т.е. будет равна потоку вектора плотности тока:

По определению заряд dQ, протекающий через поверхность S за время dt равен произведению силы тока на это время:

Видео:Что Такое Плотность Электрического Тока. Простыми Словами. Формула Плотности Электрического ТокаСкачать

Сила и плотность тока. Линии тока

Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.

Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность S .

Электрический ток является процессом движения как отрицательных, так и положительных зарядов.

Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков ( d q + и d q − ), справедливым будет заключение о том, что сила тока равна следующему выражению:

I = d q + d t + d q — d t .

В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:

где сила тока определена в качестве заряда, который пересекает некоторую поверхность S в единицу времени. В системе С И роль основной единицы измерения силы тока играет Ампер ( А ) .

Видео:Электродинамика | плотность токаСкачать

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

Выделим в проводнике, в котором протекает ток, малый объем d V случайной формы. С помощью следующего обозначения » open=» υ определим среднюю скорость движения носителей зарядов в проводнике. Пускай n 0 представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку d S , которая расположена ортогонально скорости » open=» υ (рис. 1 ).

Проиллюстрируем на поверхности площадки d S очень короткий прямой цилиндр, имеющий высоту » open=» υ d t . Весь массив частиц, которые располагались внутри такого цилиндра за время d t пересекут плоскость d S и перенесут через нее, в направлении скорости » open=» υ , заряд, выражающийся в виде следующего выражения:

d q = n 0 q e » open=» υ d S d t ,

где q e = 1 , 6 · 10 — 19 К л является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на d S d t и получим:

где j представляет собой модуль плотности электрического тока.

j = n 0 q e » open=» υ ,

где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:

j = ∑ n i q i » open=» υ i i ,

где i представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок 1 . Пускай n → представляет собой единичный перпендикуляр к плоскости d S . В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:

d q d t = j → n → d S = j n d S .

Формула приведенная выше справедлива также в том случае, когда плоскость площадки d S неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора j → , направленная под прямым углом к нормали, через сечение d S электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу j = n 0 q e » open=» υ в таком виде:

j → = — n 0 q e » open=» υ → .

Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:

где S играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника ( S 1 , S 2 ) с постоянным током справедливо следующее равенство:

j 1 j 2 = S 2 S 1 .

Основываясь на законе Ома для плотности токов можно записать такое выражение:

где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:

где интегрирование происходит по всей поверхности S любого сечения проводника. Единица плотности тока A м 2 .