Задачи на углы в окружности 8 класс

Задания предложены в двух вариантах, подходят как для формирования умений решать задачи в 8 классе, так и для подготовки к ОГЭ в 9 классе

Просмотр содержимого документа
«Задачи по теме «Углы в окружности»»

Задачи для самостоятельных работ по теме «Окружность» 8 класс.

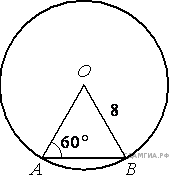
1.Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.

1) 2)3) 4) 5) 6) 7)

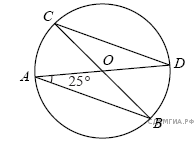
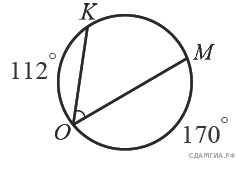
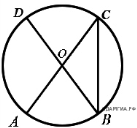
2.В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.

3.Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.

4.В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 112°. Найдите вписанный угол ACB. Ответ дайте в градусах.

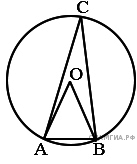
5.Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.

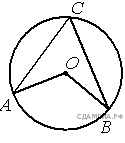
6.Точка О — центр окружности, ∠AOB=130° (см. рисунок). Найдите величину угла ACB (в градусах).

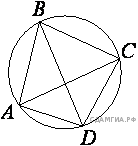
7.Четырехугольник ABCD вписан в окружность. Угол ABC равен 85°, угол CAD равен 53°. Найдите угол ABD. Ответ дайте в градусах.

1.Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 9.

1)2)3) 4)5) 6) 7)

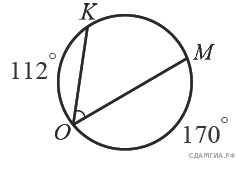
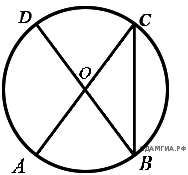
2. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 29°. Найдите величину угла OCD.

3.Найдите ∠KOM, если градусные меры дуг KO и OM равны 115° и 179° соответственно.

4. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 108°. Найдите вписанный угол ACB. Ответ дайте в градусах.

5.Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 35°.

6.Точка О — центр окружности, ∠AOB=1402° (см. рисунок). Найдите величину угла ACB (в градусах).

7.Четырехугольник ABCD вписан в окружность. Угол ADC равен 92°, угол BAC равен 48°. Найдите угол ADB. Ответ дайте в градусах.

Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Центральные и вписанные углы

О чем эта статья:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Видео:Геометрия 8 класс : Решение задач на центральные и вписанные углыСкачать

Вписанные углы окружности 8 класс задания

Видео:8 класс. Решаем задачи на центральные и вписанные углы | Часть 1Скачать

Вписанные углы окружности 8 класс задания

Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда x + 60° + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол OAB = 30°.

Найдите градусную меру центрального ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

Треугольник MON — равнобедренный. Тогда ∠MON = 180° − 2·18° = 144°.

Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Дуга FD, не содержащая точку Е, равна 360° − 150° − 68° = 142°, поэтому ∠DEF = 71°.

Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.

Так как ∠AOC и ∠AOB — смежные, ∠AOB = 180° − ∠AOC = 84°. Центральный угол равен дуге, на которую он опирается, поэтому градусная мера дуги AB равна 84°. Угол ACB — вписанный и равен половине дуги, на которую опирается, поэтому ∠ACB = 42°.

Приведем решение Артура Ахметьянова.

Треугольник AOC равнобедренный, поскольку AO = OC как радиусы окружности, тогда

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Подборка задач по теме «Окружность. Касательная. Вписанные и центральные углы»
тренажёр по геометрии (8 класс) на тему

16 опорных задач по теме «Окружность. Касательная. Вписанные и центральные углы» взяты на учебной платформе Дмитрия Гущина «Решу ОГЭ» и для удобства применения на уроке оформлены в виде таблицы. Ниже — таблица ответов.

Видео:ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Скачать:

Хочешь подготовиться к ЕГЭ за 1450 ₽ в месяц?

Вебинары Учи.Дома помогут подготовиться к ЕГЭ 2022. Поддерживающее коммьюнити из классных преподавателей, которые состоят в комиссии и знают особенности заданий изнутри. Хочешь попробовать бесплатно? Кликай по кнопке!

попробовать бесплатно, онлайн, 40 минут

Видео:Решение задач на тему центральные и вписанные углы.Скачать

Предварительный просмотр:

Окружность. Касательная к окружности. Вписанные и центральные углы.

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC , если BD = 1 см, а радиус окружности равен 5 см.

Найдите величину (в градусах) вписанного угла α , опирающегося на хорду AB , равную радиусу окружности.

В треугольнике ABC угол C равен 90°, AC = 30 , BC = 5 Найдите радиус окружности, описанной около этого треугольника.

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD , если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.

Рисунок выполнить самостоятельно

На окружности с центром O отмечены точки A и B так, что ∠ AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.

Рисунок выполнить самостоятельно

Прямая касается окружности в точке K . Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK . Ответ дайте в градусах.

Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO . Ответ дайте в градусах.

Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠ C , если ∠ A = 44°. Ответ дайте в градусах.

Из точки А проведены две касательные к окружности с центром в точке О . Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

В окружности с центром в точке О проведены диаметры AD и BC , угол OCD равен 30°. Найдите величину угла OAB .

В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B . На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB .

На окружности по разные стороны от диаметра AB взяты точки M и N . Известно, что ∠ NBA = 38°. Найдите угол NMB . Ответ дайте в градусах.

Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 66°. Найдите величину угла BOC . Ответ дайте в градусах.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD . Ответ дайте в градусах.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

По теме: методические разработки, презентации и конспекты

Вписанные и центральные углы

Активизация самостоятельности познавательной деятельности учащихся. Формирование навыков коллективной работы, развитие чувства ответственности за свои знания.

Разработка урока «Вписанные и центральные углы» 8 класс

Данная разработка включает в себя конспект урока, презентацию к уроку, самостоятельную работу, тест.

Вписанные и центральные углы

«Вписанные и центральные углыУрок изучения нового материала с применением мультимедийной презентации.

Тест по геометрии «Вписанные и центральные углы»

Тест по геометрии для учащихся 8 класса состоит из 12 заданий: выбор одного из предложенных ответов, краткая запись ответа, соответствие. На последний слайд выводится результат о решённых заданиях и в.

«Окружность. Вписанные и центральные углы.»

Презентация к уроку геометрии 8 -го класса. Материал может быть использован как в 8 классе, так и в 9 классе при подготовке к ОГЭ.

Урок по геометрии «Вписанные и центральные углы» 8 класс

Урок подготовки учащихся к успешной сдачи ОГЭ.

Тест по теме «Вписанные и центральные углы».

Тест по теме «Вписанные и центральные углы». Предназначен для повторения темы «Вписанные и центральные углы» при подготовке к ОГЭ. Состоит из 7 заданий для 2 вариантов.

Видео:ВПИСАННЫЙ УГОЛ окружности ТЕОРЕМА 8 класс АтанасянСкачать

Центральные и вписанные углы

О чем эта статья:

Видео:ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 классСкачать

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Видео:8 класс. Решаем задачи на центральные и вписанные углы | Часть 2Скачать

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Видео:Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

📹 Видео

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

8 класс. Углы в окружностиСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать