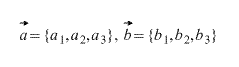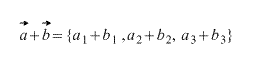Найдите координаты вектора суммы данных векторов и его абсолютную величину

1 2 3 4 5 6 7 8 9 10 11 12

1.Вектор и его абсолютная величина

Вектором называется направленный отрезок определенной длины. Любой вектор имеет начальную и конечную точки. Начало и конец вектора обозначаются заглавными буквами, например вектор

. Сам вектор обозначается прописной буквой, например:

. Каждый вектор имеет определенную длину и направление. Например, вектора

имеют одинаковое направление. А вектора

Абсолютной величиной вектора или модулем вектора называется длина отрезка, представляющего собой вектор.

Если начало вектора совпадает с его концом, то такой вектор называется нулевым.

Если два вектора имеют одинаковое направление и равные абсолютные величины, то такие векторы называются равными.

Рис.1 Обозначение векторов.

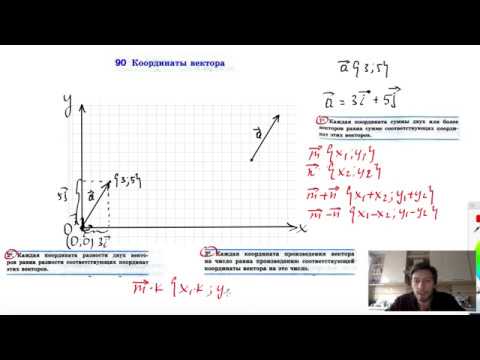
Координаты вектора

Любой вектор имеет свои координаты. Координатами вектора называются числа x₂-x₁ и y₂-y₁. Например, координаты вектора

с начальной точкой А (1;1) и конечной точкой В (4;3) будут:

Координаты нулевого вектора равны нулю.

Абсолютная величина вектора — это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е.

Два вектора называются равными, если у них соответствующие координаты равны.

Рис.2 Координаты вектора.

2.Сложение векторов

Пусть заданы два вектора со своими координатами

(b₁;b₂). Тогда суммой двух векторов будет вектор с координатами

В векторной форме можно записать так:

Для сложения векторов используются два метода: метод треугольника и метод параллелограмма.

Для сложения векторов методом треугольника необходимо перенести вектор

параллельным переносом так, чтобы конец вектора

совпадал с началом вектора

. Тогда начало вектора

и конец вектора

и будет сумма векторов

По методу параллелограмма, если два вектора

имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор

Разностью двух векторов

называется такой вектор

, который нужно прибавить к вектору

, чтобы получить вектор

Рис.3 Сложение векторов.

3.Умножение вектора на число

Любой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна:

Для любых двух векторов

число λ можно вынести за скобку λ (

Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что

Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.

Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен:

Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5)

Так как координаты вектора

(b cos α; b sin α), то скалярное произведение двух векторов

Рис.5 Скалярное произведение векторов.

Отсюда вытекает следующий вывод:

если два вектора перпендикулярны, то их скалярное произведение равно нулю.

если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.

6.Пример 1

Четырехугольник ABCD — параллелограмм. Докажите равенство векторов

Доказательство:

Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора

параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С.

Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор

переходит в вектор

. А это значит, что эти вектора равны.

Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору

Рис.6 Задача. Четырехугольник ABCD — параллелограмм.

Пример 2

Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов

Доказательство:

Найдем координаты векторов

Таким образом, координаты векторов следующие:

А так как равные вектора имеют равные соответствующие координаты и x_AB = x_CD, y_AB = y_CD, то вектора

Рис.7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).

Пример 3

В треугольнике АВС проведена медиана AM. Докажите, что

Доказательство:

, равный и параллельный вектору

от точки С. И отложим вектор

, равный и параллельный вектору

от точки В (Рис.8).

Тодга получим параллелограмм, в котором вектор

, так же как вектор

. А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то

Отсюда можно сделать вывод: так как

Рис.8 Задача. В треугольнике АВС проведена медиана AM.

Пример 4

(-3;-2). Найдите вектор

и его абсолютную величину.

Решение:

, то найдем его координаты:

Теперь найдем его абсолютную величину:

| 2 = (-1) 2 + (-4) 2 = 17

| =

(-3;-2). » alt=»Задача. Даны векторы

Рис.9 Задача. Даны векторы

Пример 5

Найдите угол между векторами

Решение:

По определению, скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними. Отсюда можно найти косинус угла между ними по формуле:

Следовательно, cos α = 2 / 2 = 1 /

Таким образом, угол между векторами

(1;-1) и b (2;0).» alt=»Задача. Найдите угол между векторами

(1;-1) и b (2;0).» src=»http://www.mathtask.ru/page-0056/pl21.png»/>

Рис.10 Задача. Найдите угол между векторами

A(2, 1)В(1, 1)С(2, — 1)Найти : Абсолютную величину и координаты вектора — 2АВ?

Геометрия | 5 — 9 классы

Найти : Абсолютную величину и координаты вектора — 2АВ.

В(1, 1) по идеи должно быть так.

Даны точки А( — 3 ; 1), В(1 ; — 2), С( — 1 ; 0)?

Даны точки А( — 3 ; 1), В(1 ; — 2), С( — 1 ; 0).

Найти : а)Координаты вектора АВ и АС.

Б)модули векторов АВ и АС.

В)Координаты вектора МК = 2АВ — 3АС.

Найти координаты вектора ВС если А 2 4 В — 2 — 6 С 0 7?

Найти координаты вектора ВС если А 2 4 В — 2 — 6 С 0 7.

A(3 ; — 2), B(1 ; — 1) найти координаты вектора АВ?

A(3 ; — 2), B(1 ; — 1) найти координаты вектора АВ.

Даны координаты точек А(6 ; — 1 ; 0), В( — 3 ; 4 ; 2) Найти : а) координаты вектора АВ и вектора ВА?

Даны координаты точек А(6 ; — 1 ; 0), В( — 3 ; 4 ; 2) Найти : а) координаты вектора АВ и вектора ВА.

Б)расстояние между точками А и В.

Найти координаты векторов?

Найти координаты векторов.

Даны векторы n(4 ; — 1) и m( — 5 ; 4)?

Даны векторы n(4 ; — 1) и m( — 5 ; 4).

Найти координаты суммы векторов n и m.

Знайти абсолютну величину вектора (4 ; 6)?

Знайти абсолютну величину вектора (4 ; 6).

Найти третью координату вектора если данные его координаты y = 4, z = — 3 и длина вектора равна 5?

Найти третью координату вектора если данные его координаты y = 4, z = — 3 и длина вектора равна 5.

Срочно?

Зарание спасибо тем кто поможет!

Даны точки А( — 2 ; 6), В( — 1 ; — 3).

1. Найти координаты вектора АВ.

2. Найти абсолютную велечену вектора а (6 ; — 8).

3. Найти длину вектора АВ, если А(3 ; 1), В(1 ; 2).

А(3 ; — 5) В( — 5 ; 1) а) найдите координаты точки О если вектор ВО = ОА б) Найдите координаты и абсолютную величину вектора ВОHepl pliss?

А(3 ; — 5) В( — 5 ; 1) а) найдите координаты точки О если вектор ВО = ОА б) Найдите координаты и абсолютную величину вектора ВО

Вы перешли к вопросу A(2, 1)В(1, 1)С(2, — 1)Найти : Абсолютную величину и координаты вектора — 2АВ?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Отрезкомназывается часть прямой, которая содержит две разные точки A и B этой прямой (концыотрезка) и все точки прямой, которые лежат между ними (внутренние точкиотрезка). Координаты точек или расстояние между ними, определяющее его длину.

Часть прямой линии, ограниченная двумя точками, называетсяотрезком. Точки, ограничивающие отрезок, называютсяконцами отрезка. Проведём прямую и отметим на ней отрезок с концамиAиB : Отрезок обозначается указанием его концов. Говорят или пишут : от..

Решение на фотографии.

Если прямаяб которую мы ищемб параллельна прямой y = 5x — 9 б то их угловые коэффициенты равныб значит искомая прямая y = 5x + b. Найдём b. Перепишем уравнение окружности в другом виде : x² + y² — 6x + 2y + 6 = 0 (x² — 6x + 9) + (y² + 2y + 1) = 4 (..

Ответ и решение на фото .

Скинь рисунок пожалуйста.

4a ^ 2 = d1 ^ 2 + d2 ^ 2a ^ 2 = (256 + 144) / 4 = 100a = 10смSп. П. / 2 = (2Sосн + 4Sбок) / 22Sосн = d1 * d2 = 192см ^ 24Sбок = 4 * 10 * 10 = 400см ^ 2Sп. П. / 2 = (192 + 400) / 2 = 296см ^ 2.

Нехай к — х. За теоремою Піфагора : (5х)² + 24² = (13х)² 25х² + 576 = 169х² 144х² = 576 х² = 4 х = 2 Р = 5х + 24 + 13х = 18х + 24 = 36 + 24 = 60 см Відповідь : 60 см.

Решение в прикрепленном файле.

4. треугольник АВС = треугольнику АСD (т. К. они имеют общую сторону АС, а противоположные стороны параллелограмма равны (AB = DC и AD = BC)) т. К. FC = EA (по условию), а AB = DC, то BE = DF что и т. Д.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

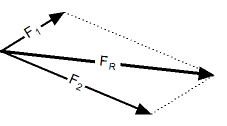Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

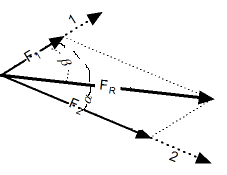Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

📹 Видео