В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
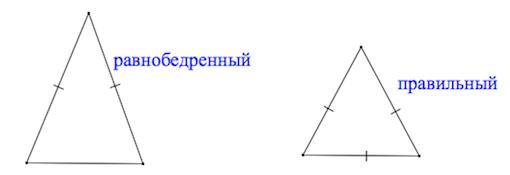
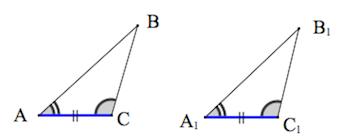
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
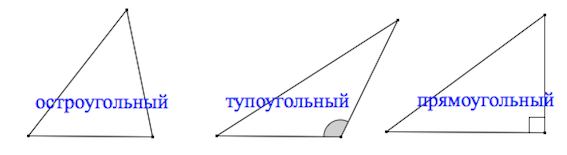
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Основание треугольника
- Стороны треугольника
- Равнобедренный треугольник
- Равносторонний треугольник
- Что мы узнали?
- Треугольник
- Треугольник произвольный
- Свойства
- Признаки равенства треугольников
- Биссектриса, высота, медиана
- Средняя линия треугольника
- Вписанная окружность
- Описанная окружность
- Соотношение сторон в произвольном треугольнике
- Площадь треугольника
- 🌟 Видео
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
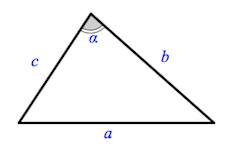
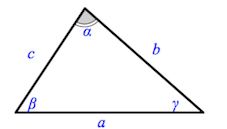
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Сколько треугольников на картинке? Расскажу, как посчитать это за 7 секунд!Скачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:Виды треугольниковСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:Сколько треугольников на рисунке? Простая задача, которая позволяет загрузить даже студентовСкачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Основание треугольника

Средняя оценка: 4.7
Всего получено оценок: 98.
Средняя оценка: 4.7
Всего получено оценок: 98.
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
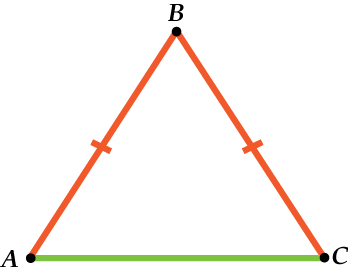
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
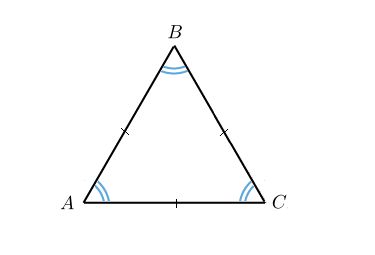
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Видео:Площади треугольников с равным углом.Скачать

Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
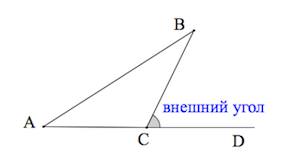
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
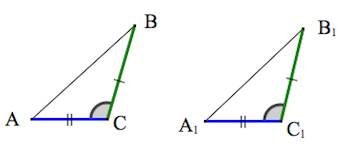
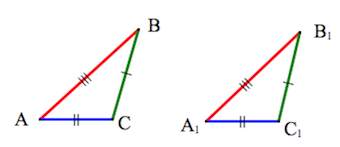
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
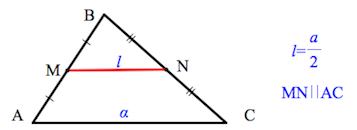
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
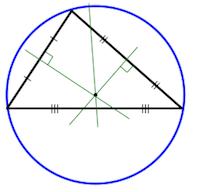
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
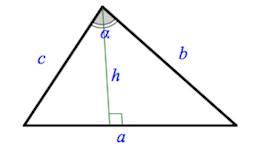
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
🌟 Видео
Как появился знаменитый треугольник Карпмана? Психологическое значение библейских историй. Лекция №2Скачать

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Как найти площадь треугольника без формулы?Скачать

Сколько треугольников на картинке?Скачать

Способ сосчитать треугольники, которому не учат в школе! Сколько треугольников на картинке?Скачать

№255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать

Виды треугольниковСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

8 класс, 14 урок, Площадь треугольникаСкачать