Как построить середину отрезка без окружностей (8 видео)

Построение середины отрезка

Пример:

Дано: отрезок АВ.

Построить: середину АВ.

Решение:

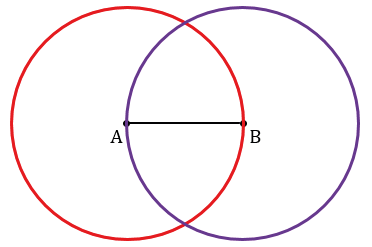
Строим с помощью линейки произвольный отрезок АВ.

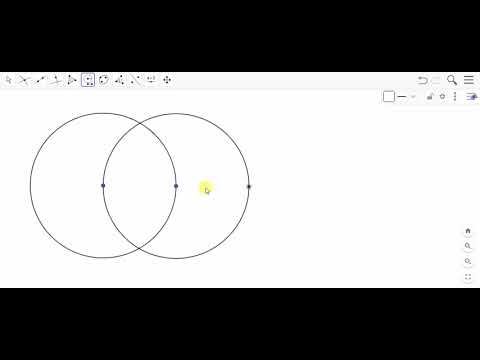
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.

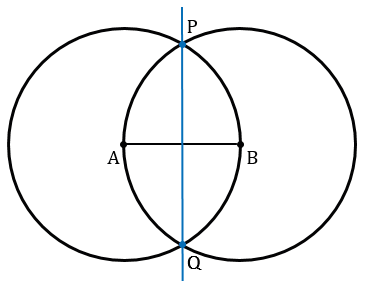
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.

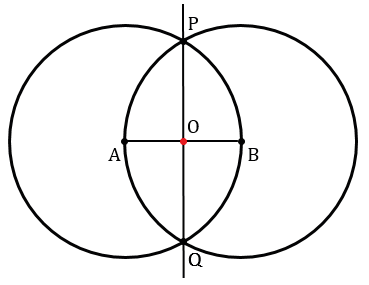
Точку пересечения прямой РQ и отрезка АВ обозначим О.

Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.

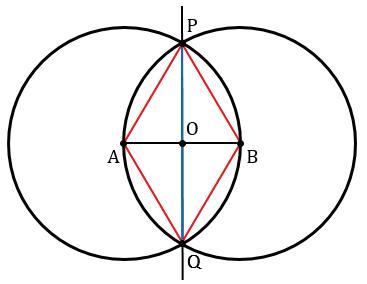
Рассмотрим треугольники РАQ и РВQ.

По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, РАQ =РВQ по 3 признаку равенства треугольников. Значит, по свойству равных треугольников АРО =ВРО, тогда РО — биссектриса АРВ.

В АРВ АР = ВР (как радиусы одинаковых окружностей), следовательно, АРВ — равнобедренный, тогда по свойству равнобедренного треугольника биссектриса РО АРВ и его медиана, следовательно, точка О — середина отрезка АВ. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Содержание

Урок№2 Тема: Построение середины отрезка. Построение перпендикулярных прямых
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Построение середины отрезка
🎬 Видео

Видео:Построение середины отрезкаСкачать

Урок№2 Тема: Построение середины отрезка. Построение перпендикулярных прямых

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Построение середины отрезкаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Тема : Построение середины отрезка. Построение перпендикулярных прямых

обучающая: научить учащихся с помощью циркуля и линейки выполнять деление отрезка пополам; сформировать умения и навыки построения перпендикулярных прямых;

развивающая: развитие пространственного мышления, внимания;

воспитательная: воспитание трудолюбия и аккуратности.

1. Актуализация основных теоретических понятий (5мин).

Сначала можно провести фронтальный опрос по следующим вопросам:

1. Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?

2. Какой треугольник называется равнобедренным? Как называются его стороны?

3. Какой треугольник называется равносторонним?

4. Что называют серединой отрезка?

Далее предложить задание: с помощью циркуля и линейки построить биссектрису, выходящую из вершины равнобедренного треугольника. Перечислить ее свойства.

2. Изучение нового материала (практическая работа) (20мин)

Построение середины отрезка

При изучении нового материала используется таблица№4 приложения 4, по которой учащиеся составляют рассказ, как разделить данный отрезок пополам. После этого в тетрадях выполняются соответствующие построения.

Задача . Построить середину данного отрезка (объясняет учитель с помощью учащихся).

Решение . Пусть АВ — данный отрезок. Построим две окружности с центрами А и В радиуса АВ (рис.5).

Они пересекаются в точках Р и Q. Проведем прямую РQ. Точка О пересечения этой прямой с отрезком АВ и искомая середина отрезка АВ.

В самом деле, треугольники АРQ и ВРQ равны по трем сторонам, поэтому 1=2.

Следовательно, отрезок РО — биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т.е. точка О — середина отрезка АВ.

Построение перпендикулярных прямых

Здесь необходимо обратить внимание, что возможны два случая:

1. Точка принадлежит прямой;

2. Точка не принадлежит прямой.

После повторения учитель формулирует задачу и объясняет построение для первого случая, при этом может быть использована таблица№3 приложения 4.

При рассмотрении второго случая учащиеся при помощи таблицы 4 проводят построение и доказательство самостоятельно.

Задача . Через данную точку О провести прямую, перпендикулярную данной прямой а (объясняет учитель, после обсуждения с учениками).

Решение . Возможны два случая:

1) точка О лежит на прямой а;

2) точка О не лежит на прямой а.

Рассмотрим первый случай (рис.6). Из точки О проводим произвольным радиусом окружность. Она пересекает прямую а в двух точках: А и В. из точек А и В проводим окружности радиусом АВ. Пусть С — точка их пересечения. Искомая прямая проходит через точки О и С.

Перпендикулярность прямых ОС и АВ следует из равенства углов при вершине О треугольников АСО и ВСО.

Эти треугольники равны по третьему признаку равенства треугольников.

Рассмотрим построение и доказательство для второго случая (рис.7).

Из точки О проводим окружность, пересекающую прямую а. Пусть А и В — точки ее пересечения с прямой а. Из точек А и В тем же радиусом проводим окружности. Пусть О — точка их пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О. Искомая прямая проходит через точки О и О. Докажем это. Обозначим через С точку пересечения прямых АВ и ОО. Треугольники АОВ и АОВ равны по третьему признаку. Поэтому угол ОАС равен углу ОАС. А тогда треугольники ОАС и ОАС равны по первому признаку. Значит, их углы АСО и АСО равны. А так как они смежные, то они прямые. Таким образом, ОС — перпендикуляр, опущенный из точки О на прямую а.

3. Закрепление (10 мин)

Задача. Постройте прямоугольный треугольник по его катетам.

Данную задачу ученик решает у доски, предварительно проведя ее анализ.

Выполним чертёж — набросок (рис.8).

2. Построение (рис.9).

1. На прямой отметим точку С и отложим отрезок СВ=а.

2. Построим прямую, проходящую через точку С перпендикулярную СВ.

3. Отложим отрезок СА=b

В АВС ВС=а, СА= b, ВDАС, следовательно, угол ВСА равен 90є. Значит треугольник АВС — искомый.

Также для отработки умений и навыков, можно использовать задачи №154 (а, б) (см. приложение 1).

4. Подведение итога (3мин)

1. В ходе урока мы решили две задачи на построение. Учились:

а) строить середину отрезка;

б) строить перпендикулярные прямые.

2. В ходе решения этих задач:

а) вспомнили признаки равенства треугольников;

б) использовали построения окружностей, отрезков, лучей.

5. На дом (2мин): №153 (см. приложение 1).

Тема: Решение задач на построение

обучающая: отработка умений и навыков выполнения элементарных построений с помощью циркуля и линейки;

развивающая: развитие пространственного мышления, внимания;

воспитательная: воспитание трудолюбия и аккуратности.

1. Проверка домашнего задания (10мин)

Проверить выполнение задачи №153.

Проверку можно организовать так: у доски три ученика, они должны построить прямую, проходящую через точку А перпендикулярно прямой а (рис.10).

Класс в это время может выполнить задание: дан треугольник АВС. построить высоту АD. После выполнения задания каждый шаг построения должен быть прокомментирован и обоснован.

2. Самостоятельная работа

Самостоятельная работа проводится по трём вариантам и имеет контролирующий характер

1. Разделить отрезок на 4 равные части.

2. Дан АВС. Построить биссектрису ВК.

3. Дан угол АОВ. Построить угол, для которого луч ОВ является биссектрисой.

Видео:Построение середины отрезкаСкачать

Построение середины отрезка

Деление отрезка пополам. Дан отрезок AB. И требуется построить его середину — точку C, лежащую на этом отрезке, и такую, что AC=BC. Для этого произвольным раствором циркуля построим первую вспомогательную дугу окружности с центром в точке A. И тем же раствором циркуля проводим вторую вспомогательную дугу окружности с центром в точке B — так, чтобы вторая дуга пересекала первую в двух точках — D и E — по обе стороны от отрезка. Соединяем точки D и E прямой — эта прямая пересекает данный отрезок. Точку пересечения называю C — это и есть требуемая середина отрезка. И вот почему: рассмотрим два треугольника : ADE и BDE. В этих треугольниках стороны AD, BD, AE и BE равны, а сторона DE — общая. Выходит, что эти треугольники равны по третьему признаку, и к тому же они оба равнобедренные . А раз эти треугольники равны, значит и соответственные углы ADE и BDE у них равны. Следовательно, в другом равнобедренном треугольнике ADB — проведённая прямая DC делит угол D на две равные части. А биссектриса DC равнобедренного треугольника — является и медианой, то есть DC — медиана , и C — середина отрезка AB. Построение закончено.