Страницы работы
Фрагмент текста работы
увидим дальше, для системы предпочтительных чисел отобраны показатели степени 5; 10; 20; 40; 80; 160.
ГОСТ 8032—84 “Предпочтительные числа и ряды предпочтительных чисел устанавливает четыре основных ряда предпочтительных чисел R5; R10; R20; R40 и два дополнительных R80; R160. Применение последних допускается только в отдельных, технически обоснованных случаях.
Государственный стандарт регламентирует установленные округленные значения как знаменателей прогрессии, так и членов всех рядов предпочтительных чисел.
Перечислим некоторые свойства основных рядов предпочтительных чисел:
1) ГОСТ 8032—84 устанавливает стандартные значения предпочтительных чисел в диапазоне 0
2) для перехода от предпочтительных чисел, таблица 1, в любой другой десятичный интервал нужно умножить эти числа на 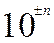
n — целое число, так при n = -1 числа переходят в интервал 0,1
3) для получения значений предпочтительных чисел каждого ряда нужно умножить единицу (вспомним требование: ряды предпочтительных чисел должны включать единицу) на соответствующий знаменатель прогрессии ряда. Дальнейшее последовательное умножение найденных чисел на знаменатель прогрессии и округление полученных значений приведет к одному из рядов. Например, для ряда R 5 первый член — 1, знаменатель прогрессии g = 1,60. Тогда второй член равен 1 ·1,60 = 1,60, третий – 1,60 ∙ 1,60 ≈ 2,50 и т.д.;
4) номер ряда предпочтительных чисел R 5, R10; R20; R40 указывает на количество чисел в десятичном интервале. Принято называть ряды с большим знаменателем и меньшим числом членов разряженными, а ряды с меньшим знаменателем и большим числом членов — густыми;
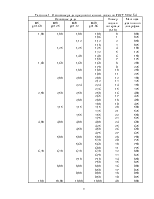
Таблица 1 — Основные ряды предпочтительных чисел по ГОСТ 8032-84
Номер числа в интервале 5
Мантисса десятичного логарифма
5) среди чисел таблицы 1 есть число 3,15, которое стандартизаторы используют в своей практике в качестве числа π= 3,I416. Использование при расчетах числа π позволяет выражать предпочтительными числами длины окружностей, площади кругов, скорости резания, цилиндрические и сферические поверхности и объемы.
Если выразить диаметр окружности d предпочтительным числом ряда R40 и умножить это число на другое предпочтительное число 3,15, то длина окружности l=πd будет представлена предпочтительным числом того же ряда;
6) в практике стандартизации следует предпочитать каждому предпочитать ряду предыдущий ряд. Ряд R5 следует предпочитать ряду R10, R10 – ряду R20 и т.д.;
7) в таблице 1 все предпочтительные числа имеют номера от 0 до 40.
Эти номера облегчают расчеты взаимосвязанных показателей стандартов, ускоряют вычисления. Номера чисел N представляют собой логарифмы предпочтительных чисел а при основании логарифмов, равном знаменателю прогрессии g
В практике вычислений для упрощения расчетов используется известное свойство логарифмов, позволяющее вместо умножения или деления самих предпочтительных чисел складывать или соответственно вычитать номера этих чисел, а по результирующему номеру определять искомое число.
Например, необходимо перемножить предпочтительные числа 2,24 и 3,55, то получим 7,952; результат требуется округлить, подвести его к стандартному значению 8,00. При пользовании же номерами предпочтительных чисел (см. таблицу 1) достаточно провести сложение:
Под номером 36 значится стандартное число 8,00.
Возведение предпочтительного числа в целую положительную или отрицательную степень производят путем умножения порядкового номера предпочтительного числа на показатель степени с последующим нахождением в таблице 1 числа, соответствующего полученному порядковому номеру. Например : 3,I5², 2N3,15 = 2 · 20 = 40. Номеру 40 соответствует число 10.
Если учесть, что при умножения предпочтительного числа табл. 1 на 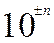
где Nт — номер числа в таблице 1
4. ВЫБОРОЧНЫЕ И СОСТАВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Приведенные выше обозначения рядов (R5; R10; R20; R40; R80; R160) характеризуют ряды не ограниченные никакими пределами.
В практике конструирования, как правило, применяются ряди с ограниченными пределами. Такие ряды обозначаются: R 20 (160 . 280) — основной ряд R20, ограниченный членом 160 в качестве нижнего предела и членом 280 в качестве верхнего предела. Пользуясь таблицей 1 запишем в развернутом виде последний ряд чисел:
Видео:15 Задача: Вычислить площадь и длину окружности круга при помощи PythonСкачать

Практическая работа (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 |
«КРИТЕРИИ ВЫБОРА ПАРАМЕТРИЧЕСКИХ РЯДОВ.»
Определение и назначение предпочтительных чисел.
Цель: Изучение свойств и особенностей рядов предпочтительных чисел.
Сколько чисел в десятичном интервале ряда R 10, R 20, R 80.
В ряде R 10 – 10 чисел,
В ряде R 20 – 20 чисел,
В ряде R 80 – 80 чисел.
Пользуясь таблицей 2, выпишите последовательно все числа ряда R 20
1 — 1,12 – 1,25 – 1,40 – 1,60 – 1,80 – 2,00 – 2,24 – 2,50 – 2,80 – 3,15 – 3,55 – 4,00 – 4,50 – 5,00 – 5,60 – 6,30 – 7,10 – 8,00 – 9,00 – 10,00…
Раскройте обозначение ряда R 20/3(0,25. 4,0) – ряд, ограниченный числами верхнего и нижнего предела
Запишите в развернутом виде ряд R 20(0,25…63). Сколько членов содержит ряд.
Ряд содержит 29 членов.
Запишите 5 членов ряда R 10/3(…25…).
Пользуясь номерами предпочтительных чисел, определите длину
окружности, если её диаметр равен d =9,5 см.
d =9,5 принадлежит ряду R 40 и имеет номер39
π≈3,15 имеет номер 20
Пользуясь номерами этих чисел можно определить искомую длину окружности.
59=40+19 используя таб. 2 определяем какие числа принадлежат этим номерам:
Перемножая эти числа определим длину окружности;
Так же найти искомую длину можно пользуясь формулой:
L = π × d =3,15×9,5=29,92 см.
Рассчитайте, пользуясь номерами предпочтительных чисел объем цилиндра. В ответе дать объем в см2. d =53см h =14 см
V=π× R 2× h =3.15×26,5×14= 33427,1см3
Критерии выбора параметрических рядов.
Цель: изучение способов обоснования параметрических и размерных рядов.
Вычислить себестоимость годового выпуска валов, длины которых назначены по ряду Ra 20.
Установить экономическую целесообразность изготовления этих валов с длинами по ряду Ra 10, Ra 40 по таблице 10.
Затраты по эксплуатации валов считать неизменными и при расчетах не учитывать ; Z =0,2.
Данные выпуска валов приведены в таблице 8; расчетные величины по требуемому ряду добавить в таблицу 8 графы 7,8.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

ОГРАНИЧЕНИЕ НОРМАЛЬНЫХ ЛИНЕЙНЫХ РАЗМЕРОВ
Основную долю применяемых в технике числовых характеристик составляют линейные размеры.
ГОСТ 8032—64 допускает округление отдельных чисел (в ряде случаев до двух округлений), что но обеспечивает требуемого уровня взаимозаменяемости и не способствует уменьшению номенклатуры линейных размеров. Из-за большого удельного веса линейных размеров и их роли в обеспечении взаимозаменяемости оказалось целесообразны самостоятельно регламентировать ряды линейных чисел, приняв в качестве базы для них предпочтительные числа и (в отдельных случаях) их
округленные значения.
ГОСТ 6636—69 Нормальные линейные размеры» является ограничительным, устанавливает обязательные для всех отраслей промышленности ряды нормальных линейных размеров. Он устанавливает все конкретные значения чисел от самого малого 0,001 до самого большого 20000 мм без деления на десятичные интервалы. Отдельные числа в этом сквозном ряду заменены округлениями значениями. Этим создаются дополнительные размеры для конструкторов, а также исключается какая-либо возможность по-разному подходить при назначении линейных размеров.
Для чисел 0,01 — 0,009 в ГОСТ 6636-69 установлен один ряд:
0,001 — 0,002 — 0,003 — 0,004 – 0,005 — 0,006 — 0,007 — 0,008 —
— 0,009. Далее линейные размеры представлены в виде четырех рядов Ra5; Ra10; Ra20; Ra40 (таблица 4); дающих размеры основного применения, и в виде дополнительных размеров, построенных на базе ряда R80, начиная о числа 1,25. Применение последних допускается лишь в отдельных, технически обоснованных случаях.
Буква «а» в наименованиях рядов означает, что отдельные предпочтительные числа в рядах заменены округленными значениями.
Ряд Ra5 образует размеры, указанные во всех столбцах строк: 1; 9; 17; 25; 33.
Ряд Ra10 образует размеры, указанные во всех столбцах строк: 1; 5; 9; 13; 17; 21; 25; 29; 33; 37.
Ряд Ra20 образует размеры, указанные во всех столбцах строк: 1; 3; 5; 7; 9; 11; 13; 15; 174 19; 21; 23; 25; 274 31; 33; 35; 37; 39.
Ряд Ra40 образует все размеры, входящие в таблицу, за исключением размеров 0,010 и 0,011.
На базе рядов, входящих в ГОСТ 6636-69, могут создаваться отраслевые стандарты и стандарты предприятия при этом допускается использование выборочных рядов путем отбора членов из рядов основного применения: Ra5; Ra10; Ra20; Ra40.
Таблица 4 — Нормальные линейные размеры по ГОСТ 6636-69
| Размеры, мм | |||||
| 1. | 0,010 | 0,100 | 1,00 | 10,0 | I0000 |
| 2. | — | 0,105 | 1,05 | 10,5 | |
| 3. | 0,011 | 0,110 | 1,10 | 11,0 | |
| 4. | — | 0,1I5 | 1,I5 | 11,5 | |
| 5. | 0,0I2 | 0,I20 | 1,20 | 12,0 | |
| 6. | 0,013 | 0,I30 | 1,30 | 13,0 | |
| 7. | 0,014 | 0,140 | 1,40 | 14,0 | |
| 8. | 0,015 | 0,I50 | 1,50 | 15,0 | |
| 9. | 0,0I6 | 0,160 | 1,60 | 16,0 | |
| 10. | 0,017 | 0,170 | I,70 | 17,0 | |
| 11. | 0,018 | 0,180 | I,80 | 18,0 | |
| 12. | 0,019 | 0,190 | 1,00 | I9,0 | |
| 13. | 0,020 | 0,200 | 2,00 | 20,0 | |
| 14. | 0,021 | 0,210 | 2,10 | 21,0 | |
| 15. | 0,022 | 0,220 | 2,20 | 22,0 | |
| 16. | 0,024 | 0,240 | 2,40 | 24,0 | |
| 17. | 0,025 | 0,250 | 2,50 | 25,0 | |
| 18. | 0,026 | 0,260 | 2,60 | 26,0 | |
| 19. | 0,028 | 0,280 | 2,80 | 28,0 | |
| 20. | 0,030 | 0,300 | 3,00 | 30,0 | |
| 21. | 0,032 | 0,320 | 3,20 | 32,0 | |
| 22. | 0,034 | 0,340 | 3,40 | 34,0 | |
| 23. | 0,036 | 0,360 | 3,60 | 36,0 | |
| 24. | 0,038 | 0,380 | 3,80 | 38,0 | |
| 25. | 0,040 | 0,400 | 4,00 | 40,0 | |
| 26. | 0,042 | 0,420 | 4,20 | 42,0 | |
| 27. | 0,045 | 0,450 | 4,50 | 45,0 | |
| 28. | 0,048 | 0,480 | 4‚80 | 48,0 | |
| 29. | 0,050 | 0,500 | 5,00 | 50,0 | |
| 30. | 0.053 | 0.530 | 5,30 | 53,0 | |
| 31. | 0,056 | 0,560 | 5,6 | 56,0 | |
| 32. | 0,060 | 0,600 | 6,0 | 60,0 | |
| 33. | 0,063 | 0,630 | 6,3 | 63,0 | |
| 34. | 0,067 | 0,670 | 6,7 | 67,0 | |
| 35. | 0,071 | 0,710 | 7,1 | 71,0 | |
| 36. | 0,075 | 0,750 | 7,5 | 75,0 | |
| 37. | 0,080 | 0,800 | 8,0 | 80,0 | |
| 38. | 0,085 | 0,850 | 8,5 | 85,0 | |
| 39. | 0,090 | 0,900 | 9,0 | 90,0 | |
| 40. | 0,095 | 0,950 | 9,5 | 95,0 |
8. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
8. 1. Какие числа называют предпочтительными? Причины их введения.
8.2. Какие стандарты базируются на рядах предпочтительных чисел?
8.3. Что называют параметрическим рядом?
8.4. Приведите примеры предпочтительных чисел, с которыми вы встречаетесь в низки.
8.5. На какой математической базе строят ряды предпочтительных чисел?
8.6. Какой недостаток арифметических прогрессий ограничивает их применение в стандартизации?
8.7. В чем особенность ступенчато-арифметических прогрессий?
8.8. Какие свойства геометрических прогрессий содействует их применению при стандартизации?
8.9. Какие требования предъявляются к рядам предпочтительных чисел, используемым при стандартизациях?
8.10. Каков должен быть конкретный вид знаменателя геометрической прогрессии, используемой в стандартизациях?
8.11. Какие ряды предпочтительных чисел устанавливает ГОСТ 8032— 84?
8.12. Для каких отраслей народного хозяйства обязательны предпочтительные числа, регламентированные ГОСТ 8032—84?
8.13. В каком интервале приведены предпочтительные числа в табл. 1?
8.I4. Каким образом, пользуясь табл.1, можно получить предпочтительное число в любом десятичном интервале?
8.15. Сколько чисел в десятичном интервале ряда R10?
8.16. Каким образом можно представить длину окружности предпочтительным числом?
8.17. Какому из основных рядов предпочтительных чисел не может принадлежать число, определяющее длину окружности?
8.18. К какой категории должен относиться стандарт, устанавливающий ряды предпочтительных чисел.
8. 19. В чем основной, смысл использования номеров предпочтительных чисел?
8.20. Какая связь существует между предпочтительными числами и их номерами?
8.21. Как определяются номера чисел для предпочтительных чисел различных десятичных интервалов?
8.22. Как обозначают ряды с ограниченными пределами?
8.23. Как образуются выборочные ряды?
8.24. Применяются ля в стандартах ступенчатые ряды?
8.25. По какому стандарту (ГОСТ 8032—84 или ГОСТ 6636—69) установлен ряд грузоподъемностей для различных типов подъемно-транспортных машин?
8.26. В каких случаях применяются производные и специальные ряды?
8.27. Приведите примеры специальных рядов.
8.28. Допускает ли ГОСТ 8032—84 построение рядов предпочтительных чисел на основе арифметической прогрессии?
9. КОНТРОЛЬНЫЕ ЗАДАНИЯ
9.1. По какой прогрессии (арифметической или геометрической) следует наладить производство двигателей внутреннего сгорания, чтобы обеспечить равномерное наращивание их мощностей? Диапазон изменения мощностей двигателей от 10 до 160 л.с. Промежуточные градации выбраны по арифметической прогрессии с разностью 25 л.с. и геометрической со знаменателем q= I,8. Общее количество градаций 7.
9.2. Возьмем два ряда предпочтительных чисел R10 и R20, Какому из них следует отдать предпочтение при первоначальном установления ряда параметров в стандарте, если при этом в первую очередь решается задача максимальной экономия средств вместе со специализацией производства?
9.3. Можно ли на базе предпочтительных чисел стандартизовать параметр, определяемый числом 33,5?
9.4. Может ля стандартное значение параметра иметь на основе предпочтительных чисел величину 32?
9.5. Определите номер предпочтительного числа 375.
9.6. Определите номер предпочтительного числа 0, 15.
9.7. Определите номер предпочтительного числа 0,0095.
9.8. Пользуясь номерами предпочтительных чисел, определите длину окружности, если диаметр равен 5,3 см.
9. 9. Может ли стандартная длина окружности равняться 63 см?
9.10. Будут ли являться членами какого—либо ряда предпочтительных чисел числа выражающие:
а) периметр и площадь квадрата, площадь поверхности и объем куба со стороной а = 2 см; 3 см;
б) периметр и площадь прямоугольника, площадь поверхности и объем параллелепипеда со сторонами а = 2 см, в = 2а, и высота параллелепипеда h= 2,5а ; 2,7а
в) периметр и площадь круга и объем шара при r = 20 мм;
г) работу и мощность силы Р = 80 Н, передвигающей тело со скоростью 3,2 м/с (векторы силы и скорости направлены в одну сторону по одной прямой);
д) момент силы Р = 31 Н, приложенной на плече l = 2,5м?
9.11. Сколько членов содержит ряд R 5 (6,3 . 40)?
9. 12. Запишите в развернутом виде ряд R ’40 (25…50).
9.13. Запишите пять членов ряда R 10/3 ( . 80 . ).
9.14. Сколько членов содержит ряд R 20/3 (0,25 . 4,0)?
9.15. Напишите обозначение ряда предпочтительных чисел, по которому построен ряд мощностей электрических машин (ГОСТ 12139-74):
100 — 125 — 160 — 200 — 250 — 320 — 400 — 500 — 630 — 800 -1000 — 1250 — 1600 — 2000 — 2500 — 3200 — 4000 — 5000 — 6300 — 8000 — 10000 Вт?
9. 16. Три конструктора, проводя расчет одного и того же изделия по общему техническому заданию, пришли к трем несколько отличающимся значениям одного из линейных размеров: 35,4 мм, 35,6 мм и 35,7 мм. Обеспечивает ля ГОСТ 8032—84 выбор всеми конструкторами единственного — для обеспечения взаимозаменяемости — стандартного размера, например, по ряду R 20?
9. 17. В какой из основных рядов предпочтительных чисел (по ГОСТ 8032—84) нельзя включить число 125?
9. 18. Определите номер предпочтительного числа 7500 (ГОСТ 8032— 84).
9. 19. Рассчитайте, пользуясь номерами предпочтительных чисел, объем цилиндра, имеющего диаметр 47,5 мм и высоту 13,2 см. Ответ дать в см³.
9.20. Укажите, как называется ряд предпочтительных чисел, по которому составлен следующий параметрический ряд:
15 — 18 — 21,2 — 25 — 30,5 — 35,5 — 42,5 — 50 — 60 — 71
9.21. Подсчитайте сколько членов содержит ряд R 10/3 (0,8 . . 800).
9.22. В процессе проектирования вала найдены его расчетные диаметр (d) и длина (l), табл. 5. По ГОСТ 6636-69 (см. таблице 2) назначить номинальные размеры его диаметра и длины. Размеры подобрать по рядам линейных размеров Rа5; Rа10; Rа20; Rа40.
Таблица 5 – Расчетные данные вала
| Вариант | |||||||||
| d, мм | 3,95 | 5,07 | 6,7 | 10,1 | 12,5 | 27,1 | 54,2 | 84,1 | 20,6 |
| l, мм | 10,2 | 20,1 | 63,5 | 72,8 |
9.23. Подсчитайте сколько членов содержит арифметический ряд
А 2 (-10 . +10); А 0,5 (0 . 40).
10. ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ
Задание 9.1. Строим два ряда мощностей:
1) 10 — 35 — 60 — 85 — 100 — 135 — 160 л.с. (по арифметической прогрессии);
2) 10 — 16 — 25 — 40 — 63 — 100 — 160 л.с. (по геометрической прогрессии). Из сравнения видно, что геометрический ряд обеспечивает более плавное наращивание мощностей и тем самым исключает появление близких по мощности двух двигателей (135 и 160 л.с.).
Задание 9.2. Основное различие между названными рядами в данной ситуации заключается в различной градации рядов. Ряд R10 более редкий, чем R=20. Включая в стандарт параметры по редкому ряду, вы снижаете номенклатуру параметров, а обеспечивая производство продукции по такому стандарту, имеете возможность специализировать производство меньшего числа номинальных значений изделий. Это в народно-хозяйственном отношении ведет к повышению серийности производства, внедрению автоматизации и механизации производственных процессов, а в результате — к повышению качества продукции, к более экономному использованию материальных средств.
Задание 9.4. Число 32 относится к тем числам, которые стандартизованы в качестве округленных значений. Необходимость в округлении ряда значений объективно существует. Представьте, например, что нужно стандартизовать число зубьев шестерни. Потребовалось, скажем, 32 зуба, а стандарт содержит предпочтительное число 31,5. Есть и другие объяснения необходимости в округленных значениях предпочтительных чисел.
Задание 9.5. N375 = N3,75 + 2 • 40 = 23 + 80 = 103.
Задание 9.8. l = πd, где d = 5,3. Воспользуемся номерами предпочтительных чисел (табл. 1):
Номер 49 представим в виде 49 = 9 + 1 • 40, т.е. в формуле (4) n = +1, что означает перенос запятой в стандартном числе таблице 1 вправо на один знак. Номеру 9 соответствует число 1,7, следовательно, номеру 49 — число 17. Ответ l = 17 см.
Задание 9.9. Да, поскольку число 63 входит в основные ряды R10; R20; R40. Из этого следует, что если диаметр выражен числом, входящим в один из этих рядов, то длина окружности l = πd будет выражена числом того же ряда и может, в частности, иметь значение 63 см.
Задание 9.13. Поскольку заданный ряд не ограничен пределами и обязательно включает член 80, отыскание остальных членов можно вести только от заданного члена как в сторону увеличения, так и в сторону уменьшения.
Пользуясь таблицей 1, выбираем из ряда R10 каждый третий член в стороны от члена 80; находим пять членов: 20 — 40 — 80 — 160 — 315.
Возможны и другие ответы. Например, 10 — 20 — 40 — 80 — 160.
Задание 9.16. ГОСТ 8032-84 не может в предложенном примере обеспечить выбор единственного стандартного размера, поскольку он допускает наряду с числами ряда R20 округления первой и второй степени. Округленные предпочтительные числа тоже стандартные, т.к. они установлены стандартом.
Выберем по ГОСТ 8032-84 стандартные числа, ближайшие к совокупности трех заданных расчетных значений. Это будут числа: 35,5 в ряду R20 (см. таблицу 1); 36,0 в ряду R’20 и 35 в раду R”20. Остановить свой выбор можно на любом из этих чисел. Если конструкторы, работая на разных предприятиях, выберут различные значения, это будет препятствовать обеспечению взаимозаменяемости деталей, изготовляемых этими предприятиями. Такой выбор размеров не допустим. Поэтому в указанном смысле ГОСТ 8032-84 имеет существенный недостаток.
Кстати, этим стандартом не пользуются при выборе стандартных чисел определения линейных размеров. Для этого разработан специальный ГОСТ 6636-69.
В машиностроении для обработки отверстий применяют металлорежущий инструмент: сверла, зенкеры, развертки, метчики и т.д.
— Если работать по ряду R5, то народное хозяйство получит значительную экономии.
Ведь для размеров в интервале от 1 до 50 мм этот ряд содержит 10 чисел и для обработки все отверстий потребуется всего 40 единиц указанных режущих инструментов;
— Если работать по ряду R160 в этом интервале содержится 285 чисел и для обработки отверстий потребуется 1140 единиц режущего инструмента. Вывод, я думаю ясен.
Но это еще не все.
При решении любого технического вопроса возникает цепная реакция.
Если все размеры деталей машин, сборочных единиц, агрегатов назначать по ряду R5, то общее число размеров по их номинальным значениям сократиться, а, следовательно, сократится огромная армия технологов, инструментальщиков, металлургов, станочников, мастеров и т.д.
1. Основы стандартизации и сертификации товаров. В.Е. Сыцко, В.В. Садовский. – Мн.: Вышэйшая школа, 2007 г.
2. Козловский Н.С., Виногоров А.Н. Основы стандартизации, допуски технические измерения. — М.: Машиностроение, 1982 г.. — 284 с.
3. Арбузова Н.В, Белоусова Л. В. и др. Стандартизация деталей и сборочных единиц общемашиностроительного применения. — М.: Изд-во стандартов, 1982 г. — 2I6 с.
4. ГОСТ 8032—84 Предпочтительные числа и ряды предпочтительных чисел.
5. ГОСТ 6636—69 Нормальные линейные размеры.
🎬 Видео
ОГЭ по математике: разбор проекта демоверсии 2023 (задания №20-25)Скачать

Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Обо всём, как образовалась вселеннаяСкачать

Показательная форма комплексного числаСкачать

Построение областей по заданным условиямСкачать

Перевод комплексного числа из алгебраической формы в тригонометрическую, показательнуюСкачать

Ю.И. Журавлев. Математические методы прогнозированияСкачать

Секреты квантовой физики, которые может решить математика.Скачать

ВСЕ ТЕОРИИ ПРОИСХОЖДЕНИЯ ВСЕЛЕННОЙ ИЛИ ИНФЛЯЦИОННАЯ ВСЕЛЕННАЯ.Скачать

Окружность, вписанная в правильный многоугольник. Видеоурок по геометрии 9 классСкачать

Теория безначальной Вселенной.Скачать

Сердобольская М.Л. - Теория вероятностей. Семинары - 3. Геометрическая вероятностьСкачать

Внешнее сопряжение прямой и окружности.Скачать

Вселенная. Квантовая физика и Биоцентризм.Скачать

Изменение порядка интегрирования в повторном интегралеСкачать

Механические передачи. Часть 1. История. Геометрия зубчатых колесСкачать

A.5.8 Системы координатСкачать

БЕСКОНЕЧНАЯ ВСЕЛЕННАЯСкачать