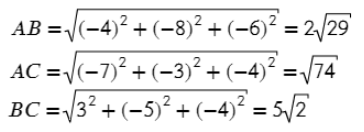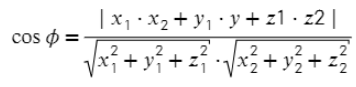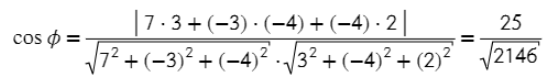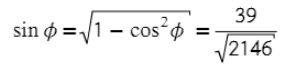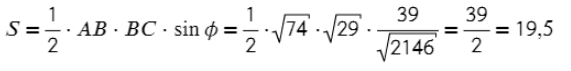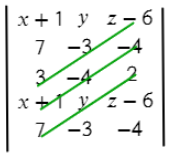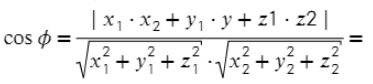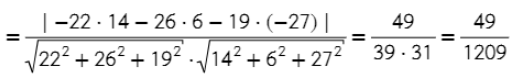Угол между вектором и плоскостью (3 видео)

Угол между прямой и плоскостью

Содержание

Формула вычисления угла между прямой и плоскостью
Вывод формулы для вычисления угла между прямой и плоскостью
Пример вычисления угла между прямой и плоскостью
Угол между вектором и плоскостью
Угол между прямой и плоскостью онлайн
Предупреждение
Угол между прямой и плоскостью − теория, примеры и решения
📸 Видео

Видео:10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

Формула вычисления угла между прямой и плоскостью

Если в пространстве заданы направляющий вектор прямой L

и уравнение плоскости

A x + B y + C z + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	\| A · l + B · m + C · n \|
	√ A 2 + B 2 + C 2 · √ l 2 + m 2 + n 2

Видео:21. Угол между прямой и плоскостьюСкачать

Вывод формулы для вычисления угла между прямой и плоскостью

Из уравнения прямой можно найти направляющий вектор прямой

Из уравнения плоскости вектор нормали плоскости имеет вид

Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой

cos ψ =	\| q · s \|
	\| s \| · \| q \|

Так как φ = 90° — ψ , то синус угла между прямой и плоскостью sin φ = cos ψ .

Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.

Видео:Угол между прямой и плоскостью. Видеоурок по геометрии 10 классСкачать

Пример вычисления угла между прямой и плоскостью

Найти угол между прямой

x — 4	=	y + 2	= —	z — 6
2	=	6	= —	3

и плоскостью x — 2 y + 3 z + 4 = 0.

Из уравнения прямой найдем направляющий вектор прямой

Из уравнения плоскости найдем вектор нормали плоскости

Воспользовавшись формулой, найдем угол между прямой и плоскостью

sin φ =	\| 2 · 1 + 6 · (-2) + (-3) · 3 \|	=
	√ 2 2 + 6 2 + (-3) 2 · √ 1 2 + (-2) 2 + 3 2

= | 2 — 12 — 9 | √ 4 + 36 + 9 · √ 1 + 4 + 9 = |-19| √ 49 · √ 14 = 19 7√ 14

Ответ: sin φ = 19 7√ 14 .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Видеоурок "Угол между прямой и плоскостью"Скачать

Угол между вектором и плоскостью

Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.

Решение задач с доказательством.

Для того, чтобы успешно решать задачи методом координат, полезно помнить:

Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.

Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.

Задача. Найти координаты и длины векторов AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).

AB = (1−5; 0-8; −3−3) = (−4; −8; −6)

AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)

BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)

Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):

Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

Находим координаты векторов.
Вычисляем косинус угла между векторами.
Через основное тригометрическое тождество получаем синус.
Подставляем в формулу площади.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)

AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)

Задача. Задайте уравнение плоскости, проходящей через точки A = ( − 4; 4; 4), B = (3; 1; 0), C = ( − 1; 0; 6).

Находим координаты векторов.
Задаем матрицу плоскости.
Вычисляем ее определитель, это и есть уравнение плоскости.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)

Первая строчка заполняется переменными x, y, z, и из них вычитаются координаты любой точки плоскости. В данном случае вычитается точка С = ( − 1; 0; 6). Тогда получится такая строка: (x−(−1); y − 0; z−6).

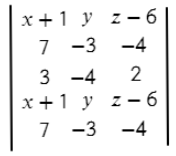
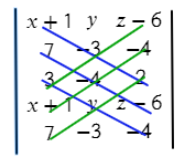
Вторая строчка — координаты первого вектора.

Третья строчка — координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).

Четвертая заполняется аналогично первой.

Пятая — аналогично второй.

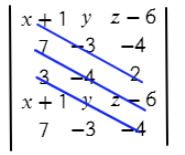
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:

Аналогично делаем с зелеными отрезками:

Осталось из значений синих отрезков вычесть значения зеленых отрезков:

= −22х −26y − 19z + 92

−22х −26y −19z + 92 — искомое уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета — это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.

Задача. Найдите угол между плоскостью, проходящей через точки A = ( − 4; 4; 4), B = (3; 1; 0), C = ( − 1; 0; 6), и плоскостью, заданную уравнением

14x + 6y − 27z + 51 = 0.

Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между прямой и плоскостью онлайн

С помощью этого онлайн калькулятора можно найти угол между прямой и плоскостью. Дается подробное решение с пояснениями. Для вычисления угла между прямой и плоскостью введите элементы уравнения и плоскости в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:21. Угол между прямой и плоскостьюСкачать

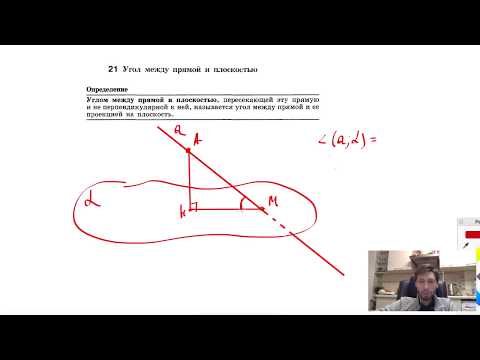
Угол между прямой и плоскостью − теория, примеры и решения

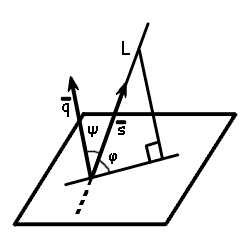
В данной статье мы рассмотрим задачу определения угла φ между прямой L, заданной каноническим уравнением

(1)

и плоскостью P, заданной общим уравнением

Ax+By+Cz+D=0.

(2)

где q=(m, l, p) направляющий вектор прямой L, а n=(A, B, C) нормальный вектор плоскости P.

Нормальный вектор плоскости n и направляющий вектор прямой q могут составить острый угол, прямой угол и тупой угол.

Вариант 1. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q острый (Рис.1):ψ Вариант 2. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q:ψ=90°. Тогда имеем:

φ=0.

0=cosψ=sinφ.

Вариант 3. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q тупой (Рис.2):ψ>90°.

cosψ=cos(90+φ)=−sinφ.

(4)

Поскольку угол φ между прямой и плоскостью всегда меньше или равно 90°, то

sinφ=⃒ cosψ ⃒

(5)

Из определения скалярного произведения векторов имеем:

(6)

Из уравнений (5) и (6) можно найти синус угла φ

(7)

(8)

Из формулы (8) можно найти угол между прямой L и плоскостью P.

Пример 1. Найти угол между прямой L:

(9)

(10)

Направляющий вектор прямой L имеет вид q=(m, p, l)=(1, 3, 2). Нормальный вектор плоскости P имеет вид n=(A, B, C)=(2, 6, 1).

Поскольку угол φ между прямой L и плоскостью P является дополнительным к углу ψ между направляющим вектором прямой q=(m,p,l) и нормальным вектором плоскости n=(A,B,C), то cosψ=sinφ. Из определения скалярного произведения (q,n)=|q||n|cosψ. Тогда для угла между прямой L и плоскостью P получим следующую формулу: