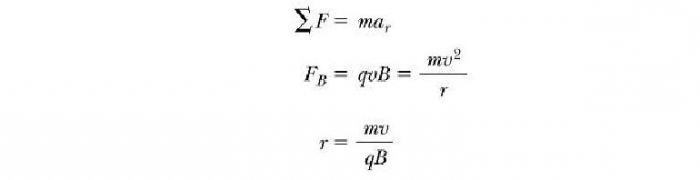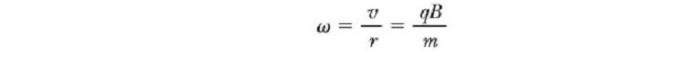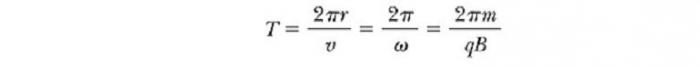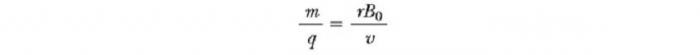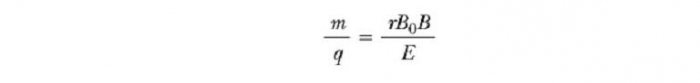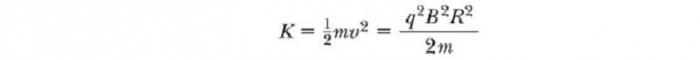Радиус кривизны окружности движения заряженной частицы

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Видео:Радиус кривизны траекторииСкачать

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Видео:радиус кривизныСкачать

Движение заряженных частиц в однородном магнитном поле

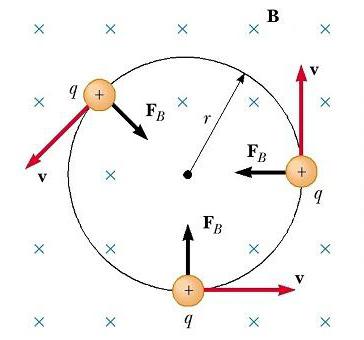
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Видео:Камень брошен горизонтально, надо искать радиус кривизны траектории. (Волькенштейн 1.20)Скачать

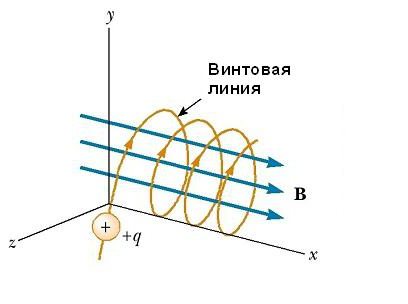
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Видео:Волькенштейн 1.21Скачать

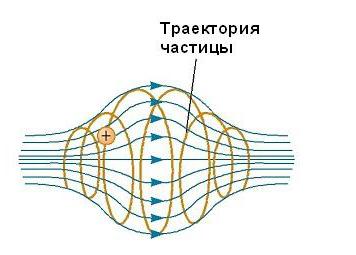
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Видео:Физика - движение по окружностиСкачать

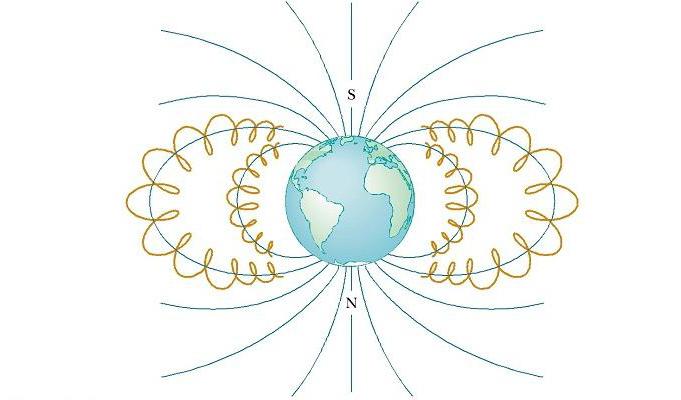
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

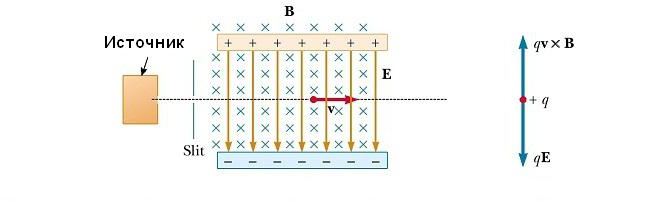
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Видео:Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Видео:Центростремительное ускорение. 9 класс.Скачать

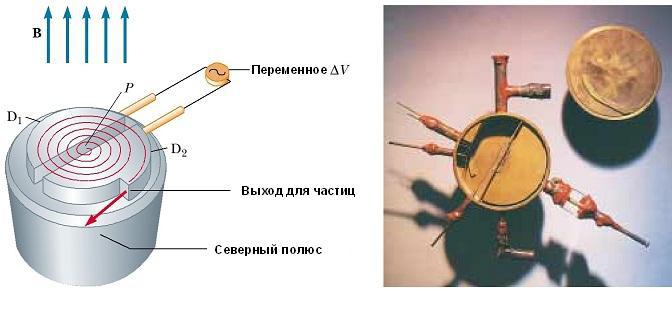
Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Видео:10.1.10. Радиус кривизны траекторииСкачать

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Видео:Электрические зарядыСкачать

Движение заряженной частицы в магнитном поле

Видео:Как находить радиус кривизны траектории #shorts #ЕНТ #ЕНТ_по_физике #Умскул #НиколайАкуловСкачать

Открытый урок объяснения нового материала. 10-й класс

Цели урока : изучить физические основы взаимодействия заряженных частиц, расширить кругозор учащихся в вопросе значения и применения магнитных полей; формировать аналитическое мышление и стремление к самостоятельному познанию окружающего мира.

Оборудование: компьютер, диапроектор, осциллограф, графопроектор, магнитофон, постоянные магниты, высоковольтный индуктор, вакуумная двухэлектродная трубка.

I. Актуализация знаний учащихся

Тестовая проверка знаний с помощью компьютера (3 человека, по желанию)

1. На рисунке изображено сечение проводника с током в точке N. Электрический ток входит перпендикулярно в плоскость рисунка. Какое из представленных в точке М направлений совпадает с направлением вектора В индукции магнитного поля?

2. Как изменится сила Ампера, действующая на прямой проводник с током в магнитном поле, при увеличении индукции магнитного поля в 3 раза и увеличении силы тока в 3 раза? Проводник расположен перпендикулярно вектору индукции.

А) Уменьшится в 9 раз; Б) уменьшится в 3 раза; В) увеличится в 9 раз; Г) увеличится в 3 раза; Д) не изменится.

3. Магнитные силовые линии:

А) начинаются на положительном заряде; Б) начинаются на южном полюсе; В) начинаются на северном полюсе; Г) начинаются на отрицательном заряде; Д) не имеют начала.

4. Если ток по проводнику идёт от нас, то магнитные силовые линии направлены:

А) к нам; Б) от нас; В) по часовой стрелке; Г) против часовой стрелки.

5. Если ток в катушке направлен против часовой стрелки. то магнитные силовые линии направлены:

А) к нам; Б) от нас; В) по часовой стрелке; Г) против часовой стрелки.

6. Магнитные силовые линии вне магнита:

А) направлены от северного полюса; Б) направлены от южного полюса; В) не имеют направления; Г) направлены от плюса к минусу; Д) направлены от минуса к плюсу.

7. Магнитные силовые линии: А) пересекаются в центре поля; Б) нигде и никогда не пересекаются; В) пересекаются на полюсах магнита.

Одновременно: решение задач по карточкам с последующей проверкой на компьютере (3 человека, по желанию, – 3 варианта)

1 вариант. На провод обмотки якоря электродвигателя при силе тока 20 А действует сила 1 Н. Определите магнитную индукцию в месте расположения проводника, если его длина 20 см. (Ответ. В = 0,25 Тл.)

2 вариант. На прямой проводник длиной 50 см. расположенный перпендикулярно магнитному полю индукцией 20 мТл действует сила 0,15 Н.(Ответ. I = 15 А.)

3 вариант. Какая сила действует на проводящую шину длиной 10 м, по которой проходит ток 7 кА, в магнитном поле индукцией 1,8 Тл. (Ответ. F = 126 кH.)

Одновременно: опрос по ранее изученным темам (учащиеся были предупреждены об опросе накануне и разделены на команды). Учитель выдаёт капитанам команд вопросы на карточках, и команды, обсудив их в течение 5 мин, сообщают ответы судьям, которые за минуту должны составить свой вердикт. Средний ряд – судьи, левый ряд – 1-я команда, правый ряд – 2-я команда.

1-я команда: что является источником магнитного поля? как направлен вектор магнитной индукции? как определяется модуль магнитной индукции? что такое сила Ампера? как определяется модуль силы Ампера?

2-я команда: какой физической величиной характеризуется магнитное поле? в чём заключается принцип суперпозиции магнитных полей? назовите единицу магнитной индукции; как определяется направление силы Ампера? где применяется сила Ампера?

Задание всему классу: определите направление силы, действующей на проводник с током, помещённый в магнитное поле, как показано на рисунке. Свяжите с географией: географические и магнитные полюсы.

II. Объяснение нового материала

Учитель. Как вы знаете, сила Ампера на практике находит широкое применение. Но электрический ток в проводнике – это движение заряженных частиц. Оказывает ли магнитное поле воздействие на эти частицы? Если да, то какое? Где мы встречаемся с эти явлением? Какова его роль? Выяснить все эти вопросы и предстоит нам сегодня. (Объявляет тему и задачи урока.) Представьте себе, что вы находитесь в лаборатории Института физики элементарных частиц. (Демонстрация отклонения пучка электронов в вакуумной трубке под действием магнитного поля.) Под действием высокой разности потенциалов поток электронов в вакууме устремляется от катода к аноду, вызывая люминесцентное свечение экрана. Создадим вокруг этого пучка постоянное магнитное поле. Что же мы наблюдаем? Поток электронов отклоняется от прямолинейной траектории. Почему это происходит? (Выслушивает мнения учеников.) Итак, магнитное поле взаимодействует с движущимися электрическими зарядами. А раз есть взаимодействие, то есть и сила, с которой осуществляется это взаимодействие. В данном случае это сила Лоренца. Теперь наша задача заключается в том, чтобы определить модуль и направление этой силы.

(Анализ траектории движения частицы с привлечением компьютера и фронтальным обсуждением. В начерченной заранее на доске таблице, где первые пять колонок с данными уже заполнены, учащиеся по мере анализа траектории движения – с использованием рисунка – заполняют три последние колонки. Первые две строки рассматриваются с помощью учителя и заполняются вызванными к доске учениками, остальные – самостоятельно по формулам, с последующей проверкой на компьютере. Программа написана учителем на бейсике. Все величины, кроме углов, приведены в условных единицах.)

С увеличением массы частицы радиус кривизны траектории увеличивается, а согласно первому закону Ньютона, увеличивается её инертность.

С увеличением магнитной индукции радиус кривизны траектории уменьшается, т.е. увеличивается центростремительное ускорение частицы. Следовательно, под действием одной и той же силы изменение скорости частицы будет меньше, а радиус кривизны траектории больше.

С увеличением заряда частицы увеличивается сила Лоренца (магнитная составляющая), следовательно, увеличивается и центростремительное ускорение.

При изменении скорости движения частицы изменяется радиус кривизны её траектории, меняется центростремительное ускорение, что следует из законов механики.

На неподвижную частицу магнитное поле не действует.

Если частица влетает в однородное магнитное поле индукцией В под углом, отличным от 90°, то горизонтальная составляющая скорости не меняется, а вертикальная составляющая под действием силы Лоренца приобретает центростремительное ускорение, и частица будет описывать окружность в плоскости, перпендикулярной вектору магнитной индукции и скорости. Благодаря одновременному перемещению вдоль направления вектора индукции частица описывает винтовую линию, причём будет возвращаться к исходной горизонтали через равные промежутки времени, т.е. пересекать её на равных расстояниях.

1. F B (определяется по правилу левой руки).

2. F = BIL sin.

I = q/t F = B(q/t)L sin.

= L/t F = Bq sin.

3. Сила, действующая на движущийся электрический заряд, называется силой Лоренца (в честь нидерландского физика-теоретика Хендрика Лоренца).

Сообщение учащегося. Хендрик Антон Лоренц (18.07.1853–04.02.1928) – создатель классической электронной теории, описывающей электрические, магнитные и оптические свойства вещества и электромагнитные явления на базе движения дискретных электрических зарядов. Эта теория позволила объяснить целый ряд физических фактов и явлений и предсказать новые. Лоренц вывел формулу, связывающую диэлектрическую проницаемость с плотностью диэлектрика, зависимость показателя преломления вещества от его плотности, дал выражение для силы, действующей на движущийся в электромагнитном поле заряд, объяснил зависимость электропроводности вещества от теплопроводности, развил теорию дисперсии света.

Лоренц исследовал также кинетическую теорию газов, твёрдых тел, предложил электронную теорию металлов и многое другое. Он был членом многих академий наук и научных обществ.

4. Определение направления силы Лоренца – по правилу левой руки. (Желающие подходят к осциллографу, подносят магнит и проверяют справедливость правила левой руки, наблюдая отклонение электронного луча на экране осциллографа.)

5. Анализ силы Лоренца.

= 90°, F B : F = qB ; пo второму закону Ньютона, она сообщает частице центростремительное ускорение (траектория движения частицы – окружность): ma = qB , m 2/R = qB R = m /qB.

а = qB /m – центростремительное ускорение;

– период;

– частота.

Специальные термины: радиус окружности, по которой движется частица в магнитном поле, – гирорадиус; траектория движения частицы – циклотронная траектория; частота обращения частицы в магнитном поле – циклотронная частота; угол между направлением вектора магнитной индукции и вектором скорости частицы – питч-угол.

= 0: F = 0 – магнитное поле не действует на неподвижный электрический заряд.

= 0: F = 0 – заряд движется прямолинейно вдоль вектора магнитной индукции.

q = 0: F = 0 – на незаряженную частицу сила Лоренца не действует.

, F и В измеряются в одной и той же системе координат.

Так как F B и B , то A = Fs = 0, т.e. магнитная составляющая силы Лоренца не совершает работы, а лишь изменяет траекторию движения
частицы.

Период и частота обращения частицы не зависят от скорости движения заряда.

Шаг винтовой спирали определяется индукцией магнитного поля, массой, зарядом и скоростью полёта заряда.

III. Сила Лоренца в природе и технике

Включаются цветоиллюминация и фонограмма: «Внимание! Внимание! Говорят все средства массовой информации Юго-Восточного округа г. Москвы! Сегодня в 10 ч утра по местному времени с космодрома „Марьинский парк” стартовал космический корабль „Мечта” с космонавтами-исследователями на борту из 10-а класса школы № 1902. Цель экспедиции – наблюдение необычных природных явлений в атмосфере. В настоящее время корабль находится в районе Северного полюса нашей планеты!»

Слайд с полярным сиянием, музыкальное вступление, учащийся читает стихи М.А.Дудина:

Ах, как играет этот Север!

Ах, как пылает надо мной

Разнообразных радуг веер

В его короне ледяной!

Ему, наверно, по натуре

Холодной страсти красота.

Усилием магнитной бури

Преображённая в цвета.

На фоне музыки – фонограмма: «После полудня было редкостное северное сияние. Когда я вышел в шесть часов, яркая дуга перекинута была над южным краем неба. Долгое время она оставалась спокойной, почти не изменяясь. Затем началось сильное свечение у её верхнего края, за чёрным гребнем горы: с минуту продолжалось пылание, затем вдруг свечение распространилось вдоль дуги на запад, к зениту ото всей ленты метнулись лучи и, не успел я опомниться, вся южная часть неба, от дуги до зенита, оказалась объята светлым пламенем. Оно сверкало и горело, кружилось, словно в вихре ветра, лучи летали взад и вперёд, то красные и красно-фиолетовые, то жёлтые, зелёные и ослепительно белые. То у основания лучи были красные, а наверху жёлтые и зелёные, то наоборот. Выше и выше поднималось пламя: вот оно достигло и северной стороны зенита – на мгновение в нём образовалась великолепная корона; потом всё обратилось в одну крутящуюся огненную массу. Это был точно водоворот огня, красного, жёлтого и зелёного, – глаз ослепляло это зрелище. » Так описывал в своём дневнике всемирно известный исследователь Фритьоф Нансен полярное сияние, наблюдавшееся в Арктике в конце 1894 г.

Учащиеся (иллюстрируют свои сообщения компьютерными слайдами, плакатами, схемами).

От Солнца во все стороны непрерывно распространяются не только волны электромагнитного излучения, но и потоки летящих с огромной скоростью заряженных частиц – солнечный ветер. Вторгаясь в атмосферу Земли, они взаимодействуют с её магнитным полем, сталкиваются с атомами и молекулами атмосферы и вызывают их свечение – полярное сияние. Состояние атмосферы Солнца всё время меняется: происходят вспышки, бушует ветер, смещаются и исчезают пятна. В этом проявляется её активность, что приводит к резкому изменению плотности и скорости распространения солнечного ветра, а это, в свою очередь, приводит к возмущению магнитосферы Земли – магнитным бурям, которые влияют не только на полярные сияния, но и на состояние атмосферы Земли и живых организмов. Магнитное поле Земли периодически (через 10 3 –10 4 лет) претерпевает инверсии – магнитные полюсы меняются местами, что не может не оказывать воздействия на эволюцию всей природы. В одной из гипотез предполагается, что разумные существа на Земле возникли миллионы лет назад именно во время резкого ослабления магнитного поля Земли и усиления солнечной активности.

– Магнитная линза – в простейшем случае это катушка, насаженная на горловину трубки, которая создаёт магнитное поле, направленное вдоль оси трубки (рассказывает, показывает по таблице).

– Действие магнитного поля на движущиеся электрические заряды плазмы используется для получения электроэнергии. Установка для магнитогидродинамического преобразования называется МГД-генератором (рассказывает, показывая по плакату).

В камере сгорания при сжигании нефти, керосина или природного газа создаётся высокая температура (2000–3000 К), при которой газообразные продукты сгорания ионизуются, образуя электронно-ионную плазму. Для повышения электропроводности плазмы в камеру сгорания вводят легкоионизирующиеся вещества, содержащие кальций, натрий, цезий. Раскалённая плазма движется по расширяющемуся каналу длиной несколько метров, её внутренняя энергия превращается в кинетическую, скорость потока возрастает до 2000 м/с. Так же, как и металлический проводник, плазма нейтральна. Влетая в область сильного магнитного поля, частицы противоположных знаков под действием силы Лоренца разделяются. Электроны, достигнув нижнего электрода, движутся во внешней цепи с резисторной нагрузкой к другому электроду, где нейтрализуют положительные ионы. Мощность, выделяемая на нагрузке, может быть использована для практических нужд.

В МГД-генераторе сильно нагрета только плазма, нет движущихся деталей, которые бы подвергались одновременному воздействию сильных механических напряжений и высоких температур (подобно лопаткам турбин). Возможность использовать огнеупорные материалы и охлаждать неподвижные соприкасающиеся с плазмой металлические детали позволяет повысить температуру рабочего тела, а значит, и КПД установки, до 60%.

Первая опытно-промышленная электростанция
У-25 с МГД-генератором мощностью 25 МВт была запущена в нашей стране в 1971 г.

– Устройство для сортировки атомов (масс-спектограф).

– Магнитная защита высокотемпературной плазмы при термоядерных реакциях (T = 10 8 К).

– Циклотроны, синхрофазотроны (ускорители). В таком ускорителе заряженные частицы – протоны, ядра атомов гелия – разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами – дуантами. Дуанты находятся между полюсами постоянного электромагнита. Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту, когда они совершат половину оборота и подойдут к зазору между дуантами, направление вектора напряжённости электрического поля изменяется на противоположное, и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности всё большего радиуса, но период их обращения остаётся неизменным. Ускорение частиц в циклотроне с постоянным периодом возможно лишь до скоростей, значительно меньших скорости света.

IV. Решение задач

1. По заданным траекториям (проекция через компьютер) движутся электрон и протон. Определите, какая траектория принадлежит каждой частице.

2. Чему равен гирорадиус протона, если гирорадиус электрона, имеющего такую же энергию, равен 5 м? Масса протона в 1840 раз больше массы электрона.

3. Циклотрон предназначен для ускорения протонов до энергии 5 МэВ. Определите наибольший радиус орбиты, по которой движется протон, если индукция магнитного поля 1 Тл.

V. Итог урока

Тестовый контроль (с помощью компьютера)

1. Как меняется радиус траектории движения частицы при уменьшении её массы в 2 раза?

А) Увеличивается в 2 раза; Б) увеличивается в 4 раза; В) уменьшается в 2 раза; Г) уменьшается в 4 раза; Д) не изменяется.

2. Каким выражением определяется сила Лоренца?

А) F = qB sin; Б) F = BILsin; В) F = ma; Г) F = BILсos. Д) Правильный ответ не приведён.

3. Если скорость движения электрона в магнитном поле равна нулю, то траектория его движения представляет:

А) окружность; Б) спираль; В) точку; Г) прямую линию. Д) Правильный ответ не приведён.

4. Сила Лоренца меняет:

А) модуль скорости движения заряда; Б) направление скорости движения заряда; В) величину магнитной индукции; Г) величину электрического заряда. Д) Правильный ответ не приведён.

5. С увеличением скорости влёта заряда в магнитное поле радиус кривизны траектории:

А) уменьшается; Б) увеличивается; В) может уменьшаться, а может увеличиваться; Г) не изменяется.

6. Модуль магнитной индукции и скорость влёта частицы уменьшились в 2 раза. Как изменился радиус её траектории?

А) уменьшился в 2 раза; Б) уменьшился в 4 раза; В) увеличился в 2 раза; Г) увеличился в 4 раза; Д) не изменился.

Определите направление движения положительного заряда по рисунку. Как изменится радиус траектории движения частицы при уменьшении её массы в 2 раза? Каким выражением определяется сила Лоренца? Если скорость движения электрона в магнитном поле равна нулю, то что представляет собой траектория движения частицы? Что изменяет сила Лоренца? Что происходит с радиусом кривизны траектории частицы с увеличением её скорости в магнитном поле? Модуль магнитной индукции и скорость влёта частицы уменьшились в 2 раза. Как изменится радиус траектории частицы?

Самостоятельное решение задач № 1097, 1098 по задачнику: Степанова Г.Н. Сб. задач по физике. 9–11-й кл. – М.: Просвещение, 1997.

Василий Петрович Новиков – выпускник МОПИ им. Н.К.Крупской 1981 г., учитель физики высшей квалификационной категории, педагогический стаж 35 лет. «Почётный работник общего образования», «Ветеран труда», награждён медалью «В память о 850-летии Москвы». Жена – учитель английского языка. Старший сын заканчивает техникум космического приборостроения, младший учится в 10-м классе.

Видео:Кривизна траекторииСкачать

Движение заряженных частиц в однородном магнитном поле

Начнём с простейшего случая — движения заряженной частицы вдоль линий индукции магнитного поля. При таком движении частицы угол а между векторами её скорости v и индукции В равен 0 или л. Поэтому по формуле (5.39) магнитная сила равна нулю, т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции — равномерно и прямолинейно.

Пусть теперь частица, имеющая заряд q, движется перпендикулярно к линиям магнитной индукции (а = 7г/2) . Тогда магнитная сила равна

и направлена перпендикулярно векторам v и В (рис. 5.22). Следовательно, частица движется в плоскости, перпендикулярной к вектору магнитной индукции, причём сила F является центростремительной силой F_nc:

где т — масса заряженной частицы, а г — радиус кривизны её траектории.

Приравняв правые части (5.65) и (5.66), найдём радиус кривизны траектории

Так как в однородном поле В = const, а численное значение скорости заряда в магнитном поле не изменяется, то радиус кривизны траектории этого заряда оказывается постоянным. Поэтому заряженная частица будет двигаться по окружности, плоскость которой перпендикулярна к магнитному полю, а радиус прямо пропорционален скорости частицы и обратно пропорционален произведению её удельного заряда — на индукцию В поля.

Направление магнитной силы и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависит от знака заряда q частицы. Если частица движется в плоскости чертежа (рис. 5.23) слева направо, а магнитное поле направлено из-за чертежа перпендикулярно к его плоскости, то при q > 0 частица отклоняется вниз, а при q 2 = const). В этом уравнении — есть нормальное

ускорение а , модуль которого равен —. Модуль силы

в данном случае qvB . Заменив в (5.72) векторы их модулями, получим уравнение

Следовательно, для периода обращения частицы

Т — ^ пГ получается формула v

Таким образом, в релятивистском случае период обращения по мере увеличения скорости уменьшается. При v «с (5.74) переходит в (5.68).

Из предыдущего следует, что траекторию заряженных частиц можно формировать с помощью магнитного поля. Этот способ широко используется во всех современных ускорителях.

🎥 Видео

Уран в камере ВильсонаСкачать

Заряд рассеиваемой частицы и форма траекторииСкачать

Движение по окружности. Ускорение. Радиус кривизны траектории.Скачать

Физика. Урок № 20. Кинематика. Ускорение и радиус кривизны траекторииСкачать

Кривизна функции. Радиус кривизныСкачать

Движение тела, брошенного под углом к горизонтуСкачать