Если прямая проходит параллельно боковому ребру призмы и пересекает верхнее основание то отрезок

Конспект урока

Геометрия, 10 класс

Урок № 14. Призма

Перечень вопросов, рассматриваемых в теме:

• Понятие призмы и виды призм;
• Элементы призмы: вершины, ребра, грани;
• Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
• Призма как модель реальных объектов;
• Пространственная теорема Пифагора.

Глоссарий по теме

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

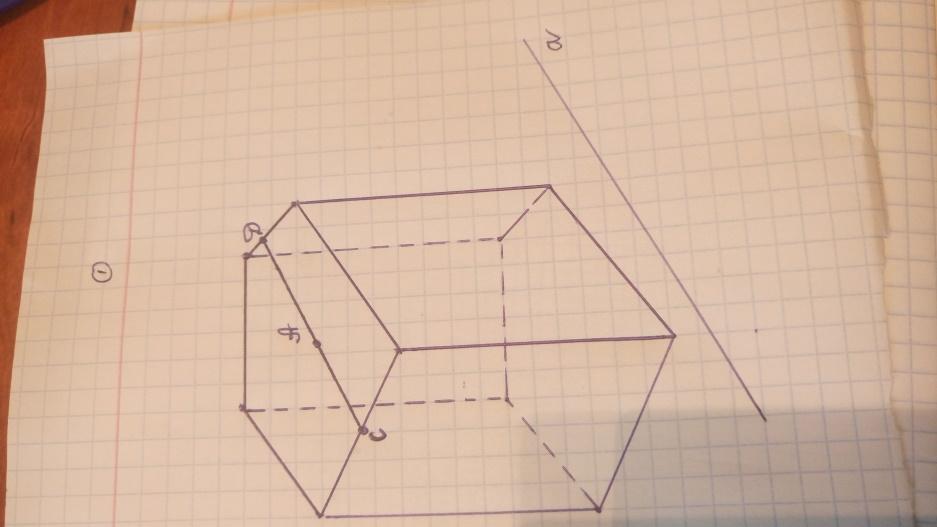
Рассмотрим два равных многоугольника А₁А₂. А_n и В₁В₂. В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂. А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Рисунок 1 – Призма

Заметим, что каждый из n четырехугольников (A₁A₂B₁B_2, . A_nA₁B₁B_n) является параллелограммом. Убедимся в этом на примере четырехугольника A₁A₂B₁B₂. A₁A₂ и B₁B₂ параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А₁В₁ и А₂В₂ по условию. Таким образом, в четырехугольнике A₁A₂B₁B₂ противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

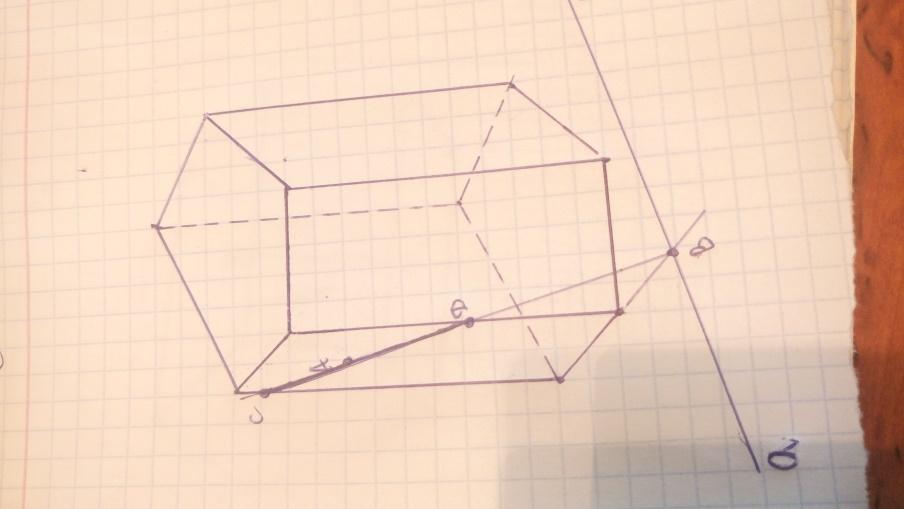
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

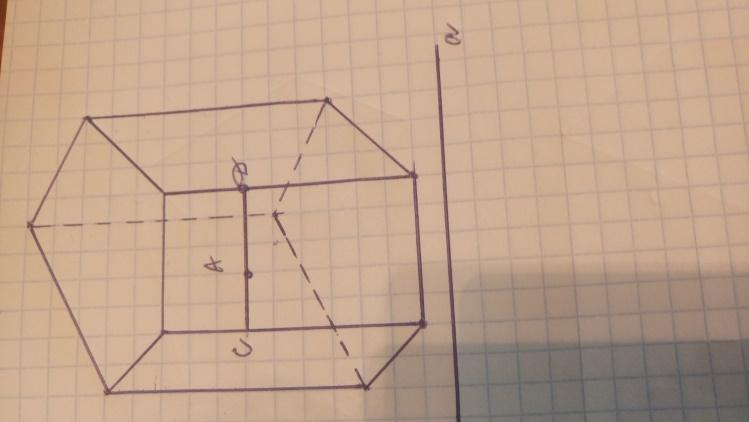
На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

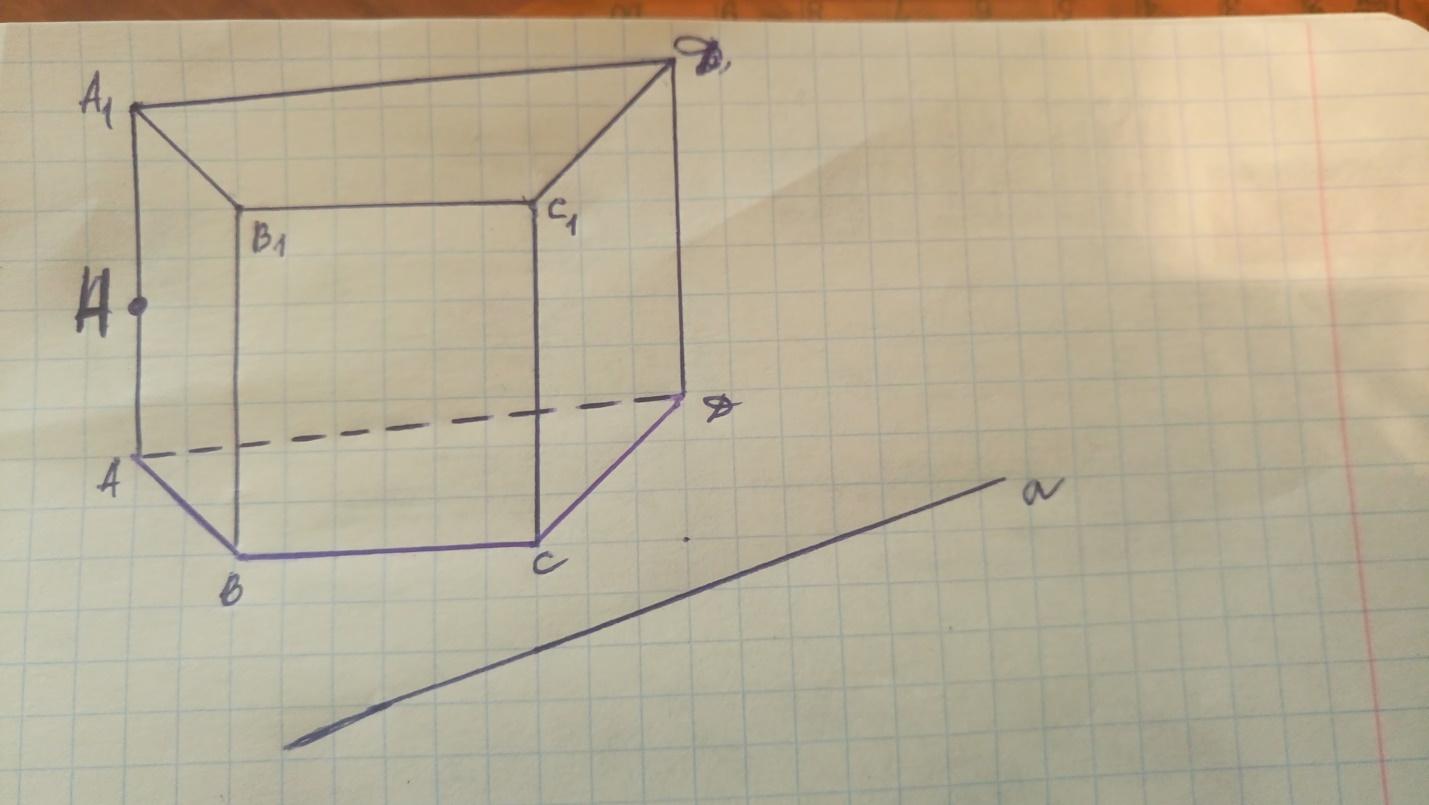
Рисунок 4 – Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С 2 =АА₁ 2 +АС 2 (1).

Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС 2 =ВС 2 +АВ 2 .

Подставив результат в (1), получим: А₁С 2 =АА₁ 2 +ВС 2 +АВ 2 .

Так как в основании прямоугольник, то ВС=АD.

Таким образом, А₁С 2 =АА₁ 2 +АD 2 +АВ 2 .

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.

Примеры и разбор решения заданий тренировочного модуля

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Справочный материал и задачи по теме «Призма»

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Выбранный для просмотра документ Призма. Справочный материал и задачи.docx

Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Указанные в определении равные многоугольники – основания призмы .

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Частным случаем призмы является параллелепипед .

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике

Вопросы для повторения:

— Что называется многогранником?

— Из каких частей состоит многогранник?

— Что называется гранью многогранника?

— Что называют диагональю многогранника?

Общие теоретические сведения

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и n параллелограммов .

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

Свойства призмы .(слайд 5)

Основания призмы являются равными многоугольниками.

Боковые грани призмы являются параллелограммами.

Боковые ребра призмы параллельны и равны.

Различают призмы прямые,наклонныеи правильные. (слайд 6,7,8)

Диагональным сечением призмы называется ее сечение плоскостью, проходящей через два боковых ребра, которые не лежат в одной грани.

Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение называется перпендикулярным сечением призмы.

Площадь боковой поверхности призмы равна сумме площадей ее боковых граней.

Площадь полной поверхности призмы равна сумме площадей оснований и площади боковой поверхности.

.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

.

Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.

.

, где S – площадь основания, H – высота призмы.

Объем призмы можно найти, умножив площадь перпендикулярного сечения на длину бокового ребра. .

Частным случаем призмы является параллелепипед.

Параллелепипед– это призма, основаниями которой являются параллелограммы

Различают прямой, наклонный, прямоугольный параллелепипеды.

Длины непараллельных ребер прямоугольного параллелепипеда называют его линейными размерами (измерениями).

У прямоугольного параллелепипеда три измерения.

Объём прямоугольного параллелепипеда равен произведению трех его измерений.

Повтори необходимые формулы :

1. Прямоугольный параллелепипед

Пусть a, b, с – стороны, d – диагональ параллелепипеда,

S_n – полная поверхность.

d 2 = a 2 + b 2 + c 2

Пусть a – реброкуба .

d=a

Ответь на теоретические вопросы по теме «Призма»

Ребро куба равно a. Найдите: диагональ грани, диагональ куба, периметр основания, площадь грани, площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из одной и той же вершины. (слайд 14)

Площадь боковой поверхности правильной четырёхугольной призмы равна 32 см 2 , а площадь полной поверхности 40 см 2 . Найдите высоту призмы. (слайд 15)

Расстояния между боковыми рёбрами наклонной треугольной призмы равны 2 см, 3 см и 4 см. Боковая поверхность призмы 45 см 2 . Найдите боковое ребро. (слайд 16)

В правильной n – угольной призме проведена плоскость под углом 60 0 к основанию так, что она пересекает все боковые грани призмы. Площадь основания равна 50 см 2 . Найдите площадь сечения.

Существует ли призма, имеющая 50 рёбер? 54 ребра?

Решение: Число ребер n – угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существует, а 54 ребра имеет 18-угольная призма.

В правильной треугольной призме плоскость сечения BCА₁ образует с плоскостью основания двугранный угол φ. Постройте линейный угол этого двугранного угла. Дайте объяснение.

Построение: Проведём из вершины A правильного треугольника ABC высоту AK. Точка K принадлежит ребру BC. Соответственно, отрезок А₁К перпендикулярен ребру BC (по теореме о трёх перпендикулярах). Угол A₁КА– искомый.

Задания части В.

1. Объем прямоугольного параллелепипеда равен 2. Чему будет равен объем параллелепипеда, если каждое его ребро увеличить в 3 раза.

Решение. Пусть ребра данного параллелепипеда равны a, b и c. Тогда имеем: V=abc=2. После увеличения каждого ребра в 3 раза его объём будет равен

V=3a*3b*3c =27 abc=27*2=54.

2. Аквариум имеет форму прямоугольного параллелепипеда высотой 30 см. Если в него налить 30 л. воды, то до верхнего края останется 5 см. Сколько литров воды нужно, чтобы наполнить пустой аквариум доверху?

Решение. Пусть V и H соответственно объем и высота параллелепипеда.

V=SH . По условию V=30,H=25, тогда 25*S=30.

После заполнения пустого аквариума доверху H=30. Значит, 30*S=V.

Найдем отношение =, V=36 л.

3. Кубик весит 10 гр. Сколько граммов будет весить кубик, ребро которого в 3 раза больше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала.

Решение. Пусть V- объём данного параллелепипеда. После увеличения каждого ребра в 3 раза, его объём будет равен 27 V.

, x=270 гр.

Задания части С.

В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AС₁ и плоскостью BСC₁.

Из точки А опускаем перпендикуляр.

Т.к. , , то и

Тогда AC₁ – наклонная, ВС₁– проекция прямой AC₁ на плоскость BСC₁. Т.к. угол между прямой и плоскостью – это угол между этой прямой и её проекцией на плоскость, то — искомый.

Треугольник ABC₁— прямоугольный.

.

Пусть сторона куба равна a. Тогда .

.

Ответ: .

2.Сторона основания правильной призмы ABCDA₁B₁C₁D₁ равна 12, а боковое ребро.Найдите градусную меру угла между плоскостями AB₁C и ABC.

Плоскость AB₁C пересекает плоскость ABC по прямой AC. Построим линейный угол двугранного угла между этими плоскостями.

Для этого из точки B проведём перпендикуляр к прямой AC. Т.к. призма правильная, то её основанием является правильный четырёхугольник – квадрат. Диагонали квадрата взаимно перпендикулярны, следовательно, искомый перпендикуляр-отрезок BO – половина диагонали BD, причём точка O – середина отрезка AC.

Т.к. призма правильная, то она прямая, значит, боковые рёбра перпендикулярны плоскости основания. Следовательно, BO — проекция наклонной B₁O. По теореме о трёх перпендикулярах наклонная B₁O перпендикулярна прямой AC.

Следовательно, угол BOB₁ является линейным углом двугранного угла между плоскостями AB₁C и ABC.

В квадрате ABCD AB=12, BD=, BO=:2 =

Рассмотрим треугольник BB₁O.

, а значит, прямая BB₁ перпендикулярна любой прямой, лежащей в плоскости ABC. Поэтому треугольник OBB₁ -прямоугольный, а значит

, следовательно, .

3. В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁найдите угол между плоскостью АА₁С и прямой А₁В, если АА₁=3, АВ=4, ВС= 4.

Решение. Из точки В проведем перпендикуляр ВН к АС. А₁Н – проекция А₁В на плоскость АА₁С. Значит, угол ВА₁Н- искомый.

Из прямоугольного треугольника АВС находим ВН=2.

Из прямоугольного треугольника А₁АВ находим А₁В= 5.

Из прямоугольного треугольника А₁НВ находим sinА₁==

Ответ: arcsin.

Задачи для самостоятельного решения.

1. Объём прямоугольного параллелепипеда равен 32. Чему будет равен объём

параллелепипеда, если каждое его ребро уменьшить в 2 раза. (4)

2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 36 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд той же формы, у которого сторона основания в 3 раза больше, чем у первого. Ответ выразите в сантиметрах. (4)

3. Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами 30, 40 и 45 см. стоит на горизонтальной поверхности таким образом, что наименьшая грань является дном. В сосуд налили воду до уровня 36 см. На каком уровне окажется вода, если сосуд поставить на наибольшую грань? Ответ дайте в сантиметрах. ( 24 )

4. В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AA₁ и плоскостью BC₁D. ()

5. Основание прямой призмы АВСА₁В₁С₁— треугольник АВС, в котором, ВС=2, sinА=0,3. Высота призмы равна. Найдите синус угла между прямой ВС₁ и плоскостью АСС₁. ( 0,2)

6. В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6 см., и углом при вершине 120º. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10 см. Найдите площадь боковой поверхности. (48 +32)

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Построение сечений призмы

Построение сечений — достаточно сложная тема для учащихся. Данная разработка урока посвящена построению сечений призмы, включая метод следов

Просмотр содержимого документа
«Построение сечений призмы»

Сечение призмы плоскостями

рассмотреть основные простейшие виды сечений призмы, рассмотреть теорию метода следов и применить ее для построения более сложных сечений.

Воспитательные: воспитание самостоятельности, умения слушать, анализировать и делать выводы

Развивающие: развитие пространственного воображения, навыков самоорганизации, работы в парах при выполнении домашнего задания, умения анализировать, обобщать и делать выводы.

Оборудование: компьютер, мультимедийный проектор, доска и мел.

Организационный момент (сообщение темы урока, актуальности темы и целей урока)

Учитель: Прежде чем говорить об актуальности темы, давайте ответим себе на несколько вопросов:

Что такое многогранник?

Ответ: Многогранник это тело, поверхность которого состоит из нескольких многоугольников.

Что такое призма?

Ответ: призма это многогранник, состоящий из двух многоугольников, лежащих в параллельных плоскостях и совмещаемых параллельным переносом и всех отрезков соединяющих соответствующие точки этих многоугольников.

Что такое сечение?

Ответ: Сечением поверхности геометрических тел называется плоская фигура, полученная в результате пересечения тела плоскостью и состоящая из точек принадлежащих как секущей плоскости так и из точек самой поверхности данного тела.

Вот теперь поговорим, для чего нужны сечения и где они встречаются?

В математике нет ни одной темы, которая бы не находила своего широкого применения на практике. Так вот, построение сечений не является исключением. Очень часто с сечение различных геометрических тел встречаются в инженерии, в строительстве итд. Более того, порой недостаточно уметь просто строить эти сечения, а также необходимо уметь вычислять например площадь или периметр этого сечения. Так же задания на построение сечений и вычисление его элементов встречаются в программе профильного уровня ЕГЭ в рамках задачи №16, и как показывает практика, эти задания вызывают большие трудности у выпускников. Именно поэтому, изучение данной темы необходимо на достаточно углубленном уровне.

Итак, перейдем к рассмотрению темы и следующий вопрос будет такой:

Каким способом можно задать секущую плоскость?

Через три точки можно провести плоскость и притом только одну

Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну

Через две пересекающиеся прямые можно провести плоскость и притом только одну

Через две параллельные прямые можно провести единственную плоскость.

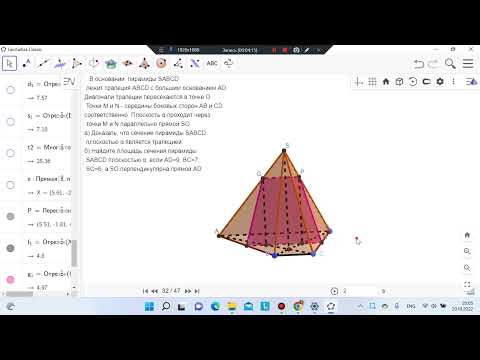
А сейчас рассмотрим самые простейшие виды сечений призмы:

Это сечение параллельное основаниям. В сечении получается многоугольник, равный основаниям.

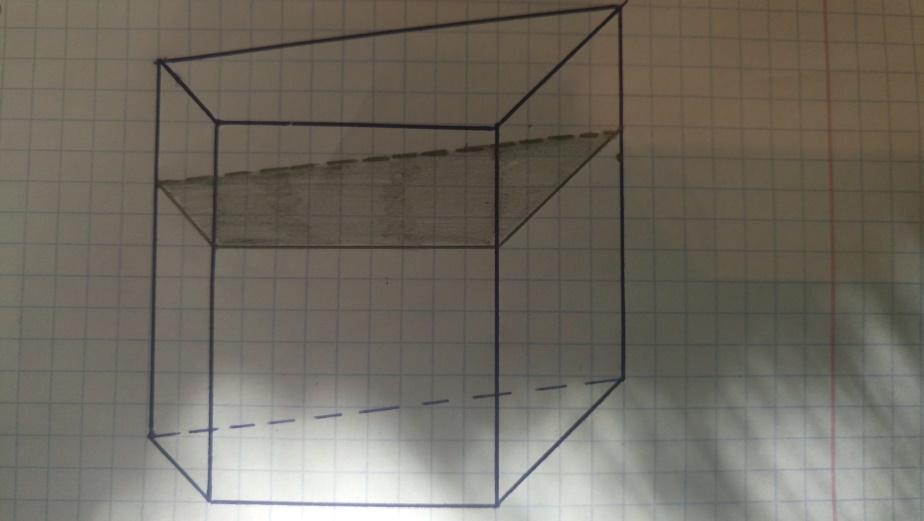
На этом чертеже построено сечение призмы плоскостью, параллельной боковой грани. Оно представляет собой параллелограмм.

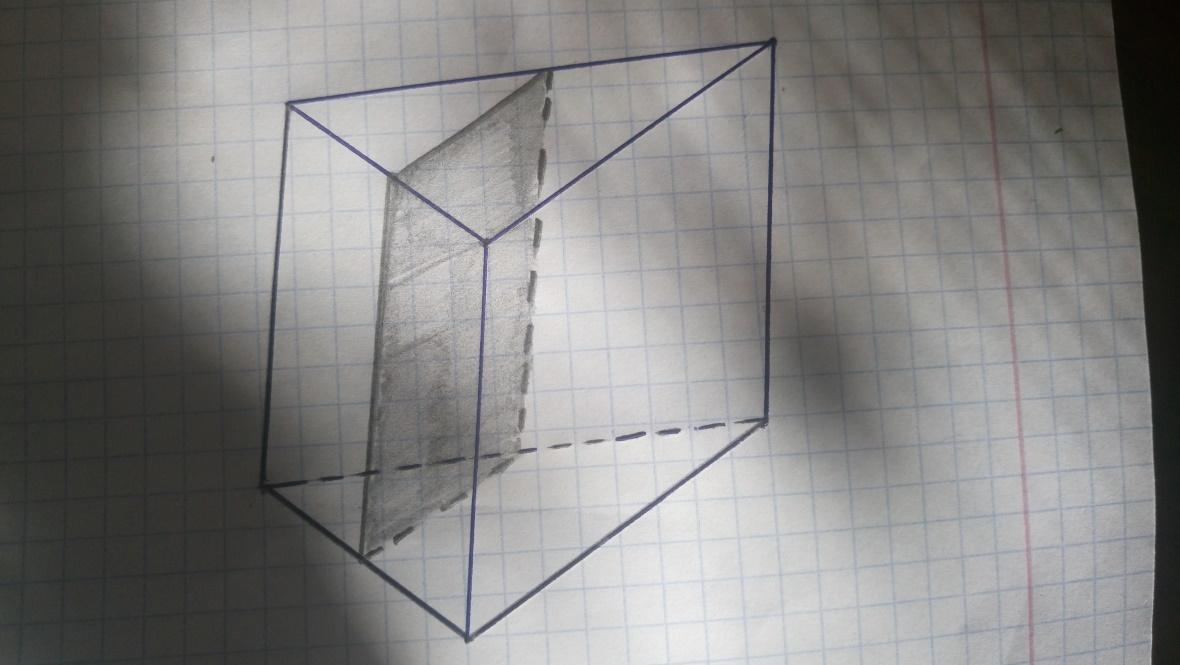
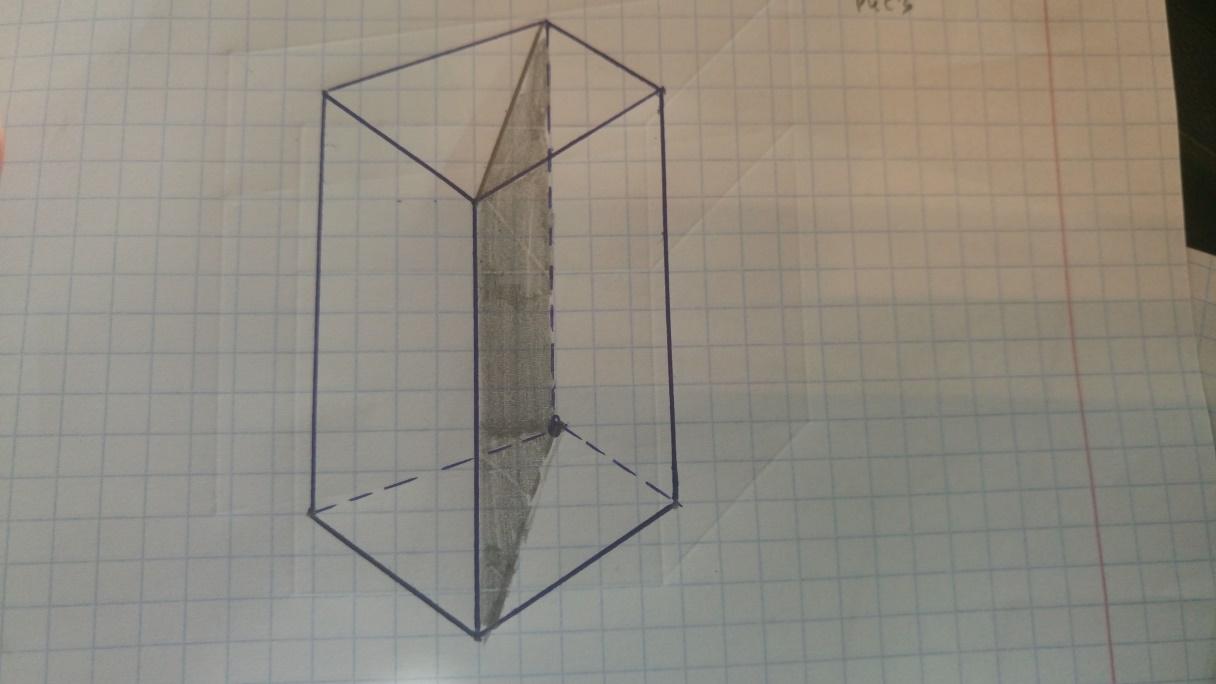
А на этом чертеже построено так называемое диагональное сечение. Это сечение, проходящее через два боковых ребра, не принадлежащие одной грани. Оно представляет собой параллелограмм.

Для построения более сложных сечений призмы может и пользоваться метод следов, где основа всего метода в следе секущей плоскости.

Следом секущей плоскости называется прямая пересечения секущей плоскости и плоскости основания призмы.

Суть метода следов состоит в применении ряда правил построения сечений:

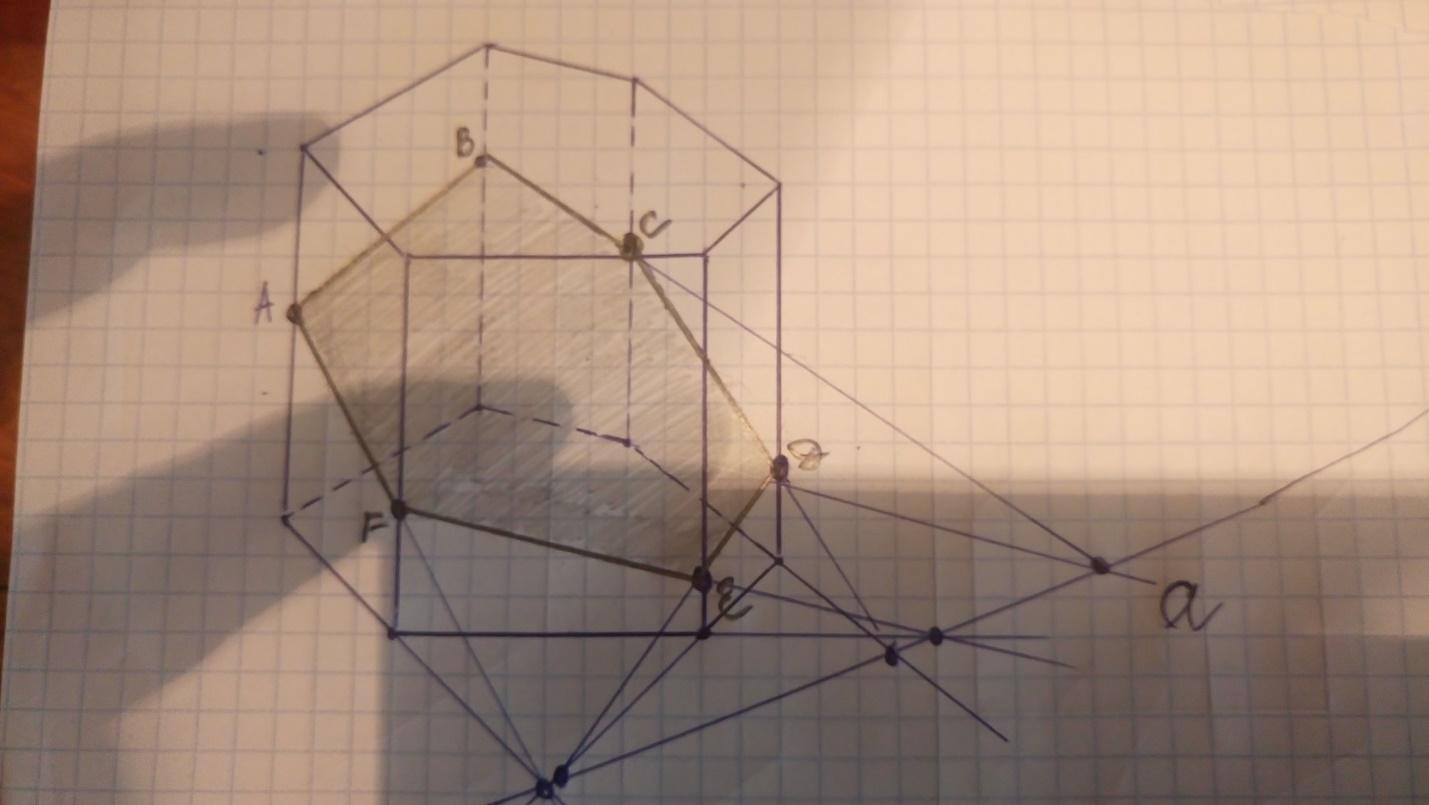
Пусть дана пятиугольная призма, точка А, принадлежащая верхнему основанию призмы и секущей плоскости и след а секущей плоскости, принадлежащий плоскости нижнего основания.

Тогда пересечение секущей плоскости верхнего основания будет представлять собой отрезок СД, проходящий через точку А, параллельный следу а.

Пусть снова дана пятиугольная призма. Если точка А принадлежит боковой грани, то пересечение этой грани с секущей плоскостью, проходящей через точку А строится так:

Строим точку В, в которой плоскость грани, пересекает след а

Затем проводим прямую АВ. Она пересекает грань по отрезку СД.

Отрезок СД и есть пересечение этой грани с секущей плоскостью, проходящей через точку А

Если грань, содержащая точку А параллельна следу а, то секущая плоскость, пересекающая эту грань и проходящая через точку А,пересекает эту грань по отрезку СД, параллельному следу а.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. Таким образом можно получить многоугольник, который и окажется сечением призмы. В использовании этих трех правил и состоит суть метода следов для построения сечения призмы.

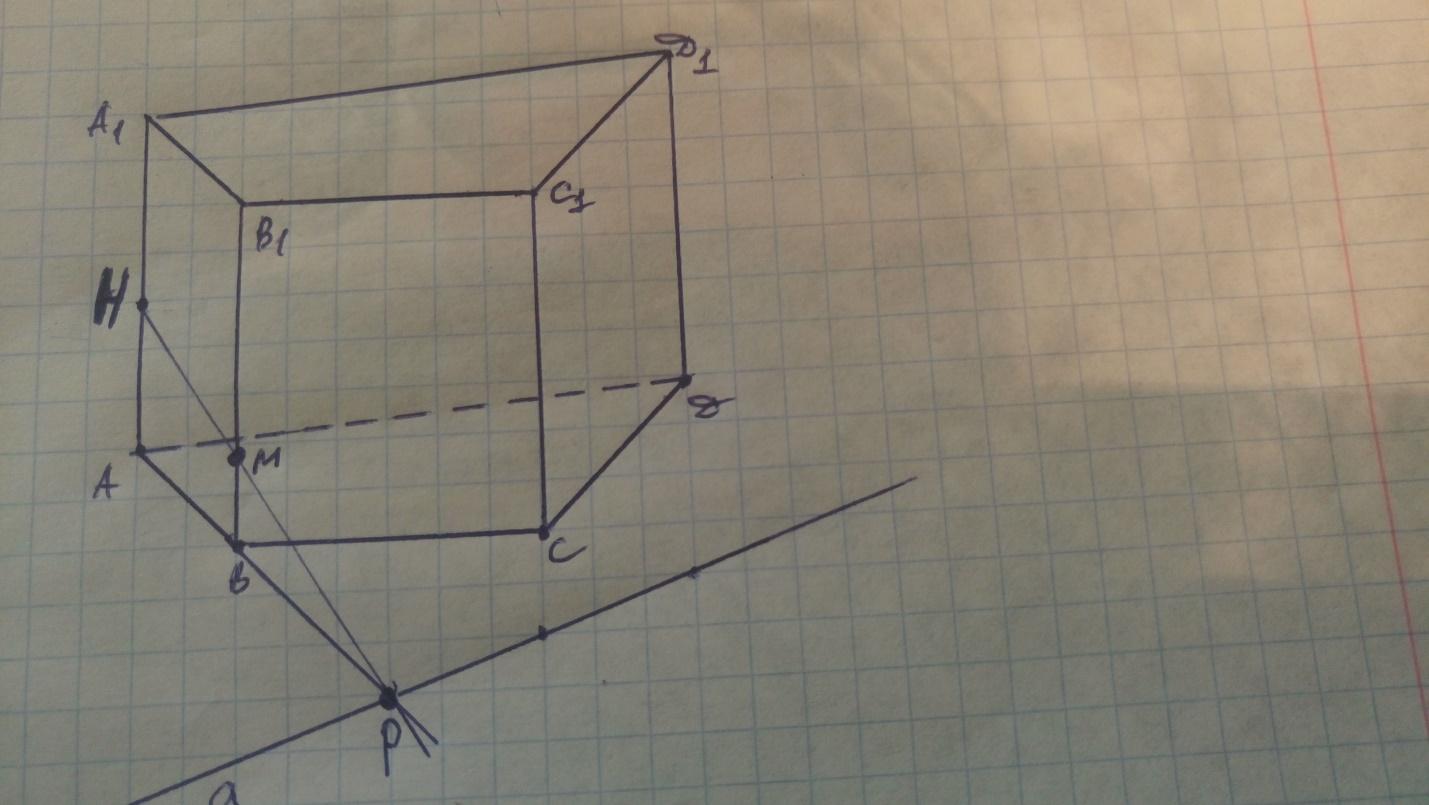
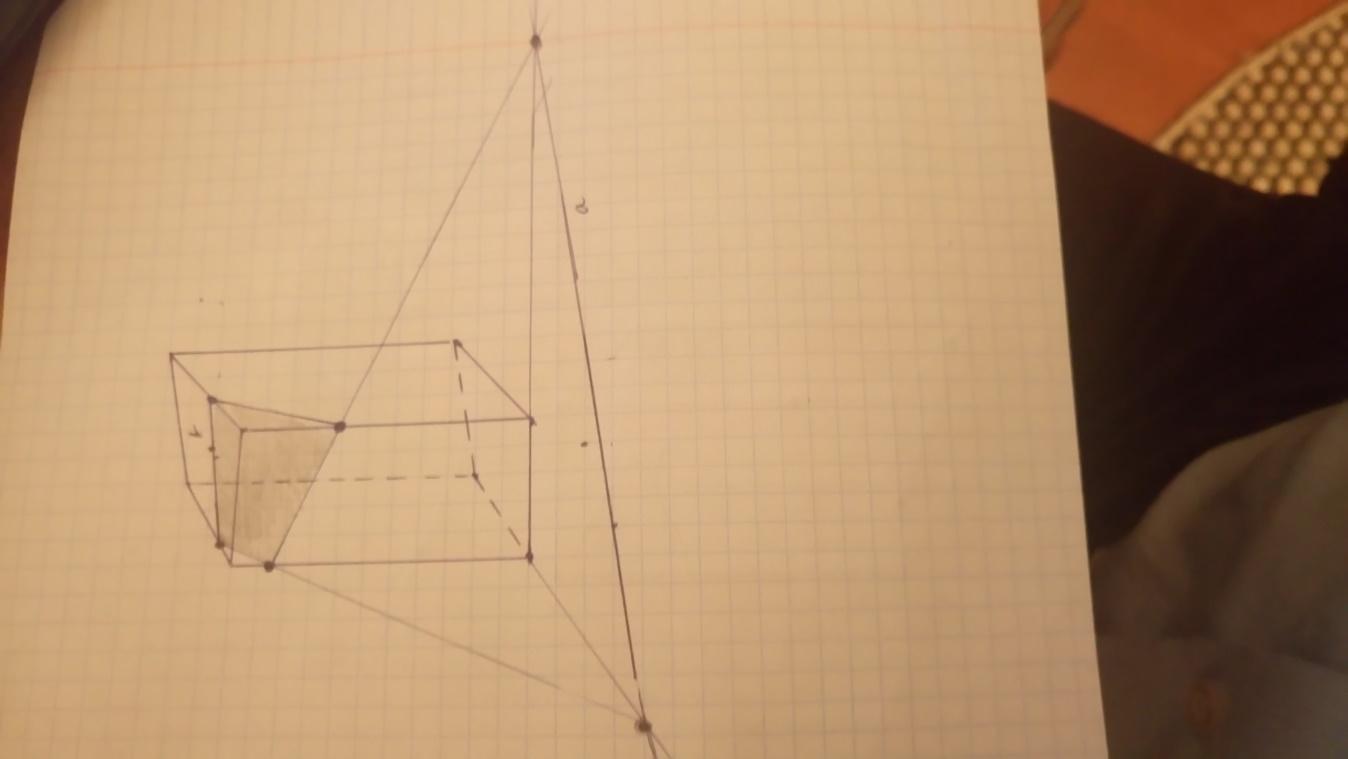
Построить сечение четырехугольной призмы плоскостью, проходящей через прямую а, лежащей в плоскости нижнего основания и точку Н, принадлежащей боковому ребру.

Очевидно, что прямая а это и есть след секущей плоскости.

Точка Н принадлежит грани (АВВ₁), поэтому строим точку Р, в которой плоскость этой грань пересекает след а.а именно след пересекает прямая АВ. затем строим прямую РН, которая пересечет данную грань по отрезку НМ.

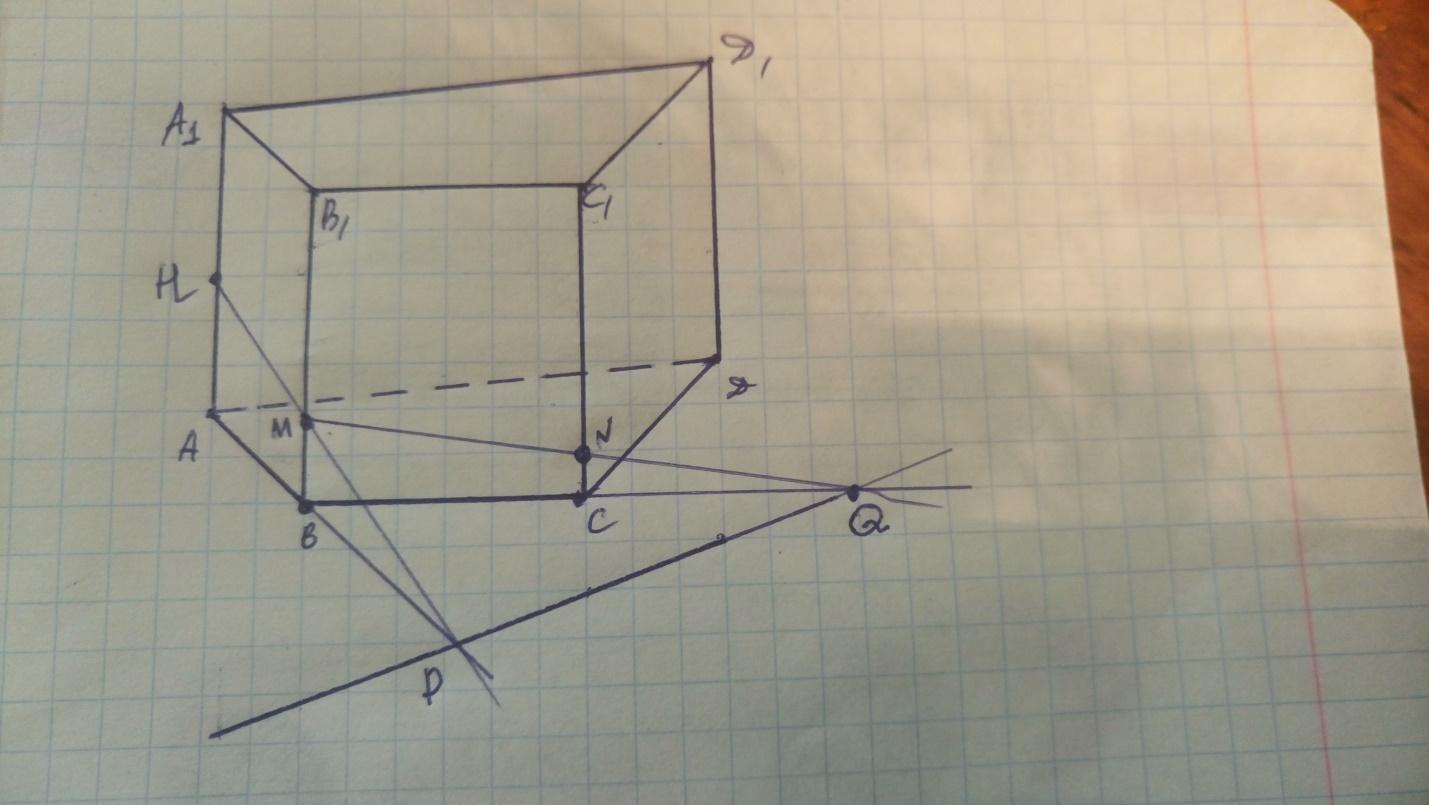
Далее, так как точка М принадлежит грани (ВСС₁),то проводим ВС, которая пересечет след в точке Q. Проводим QM, пересекающую грань по отрезку MN.

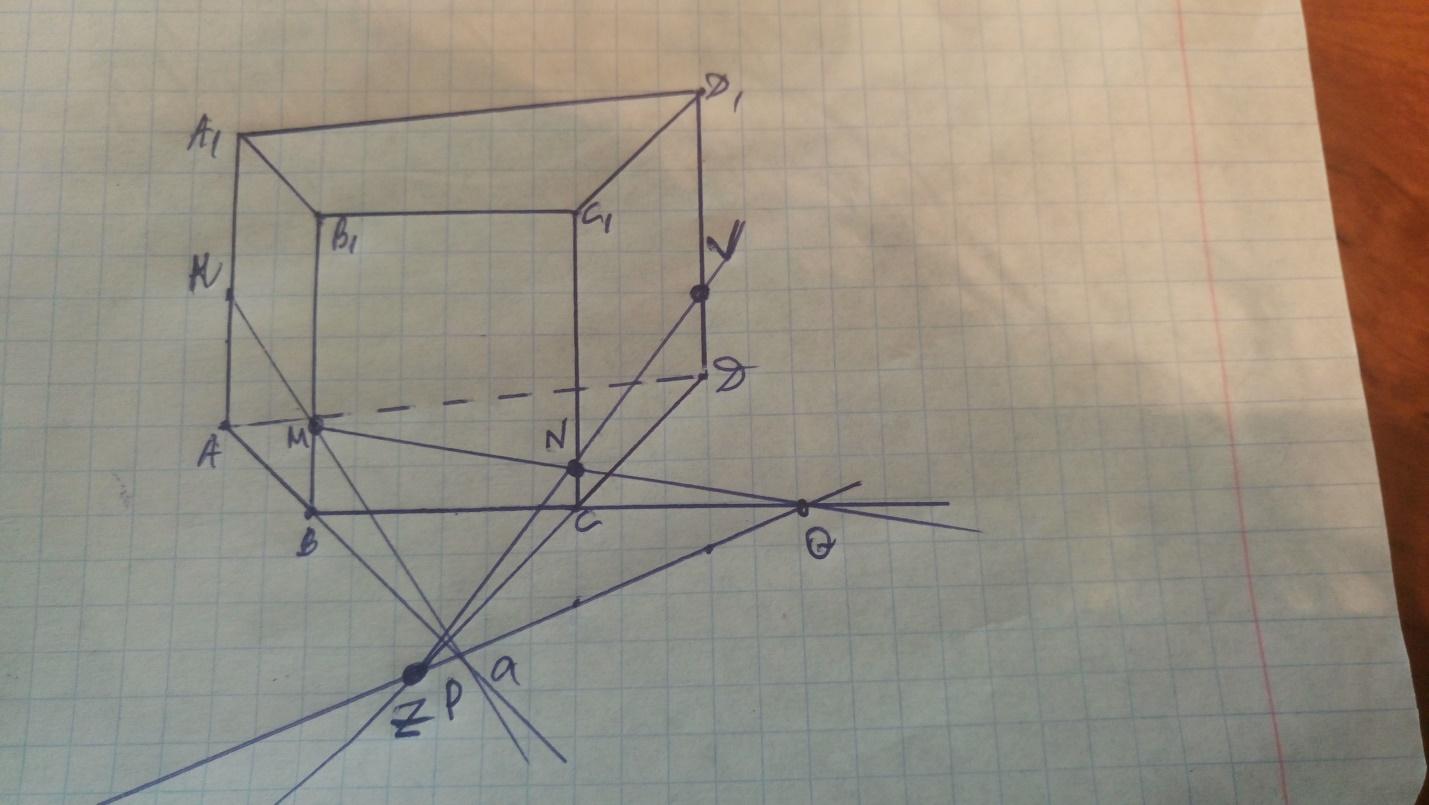
Точка N принадлежит грани (СДД₁), поэтому проводим СД пересекающую след а в точке Z, затем проводим ZN, пересекающую грань призмы по отрезку NV.

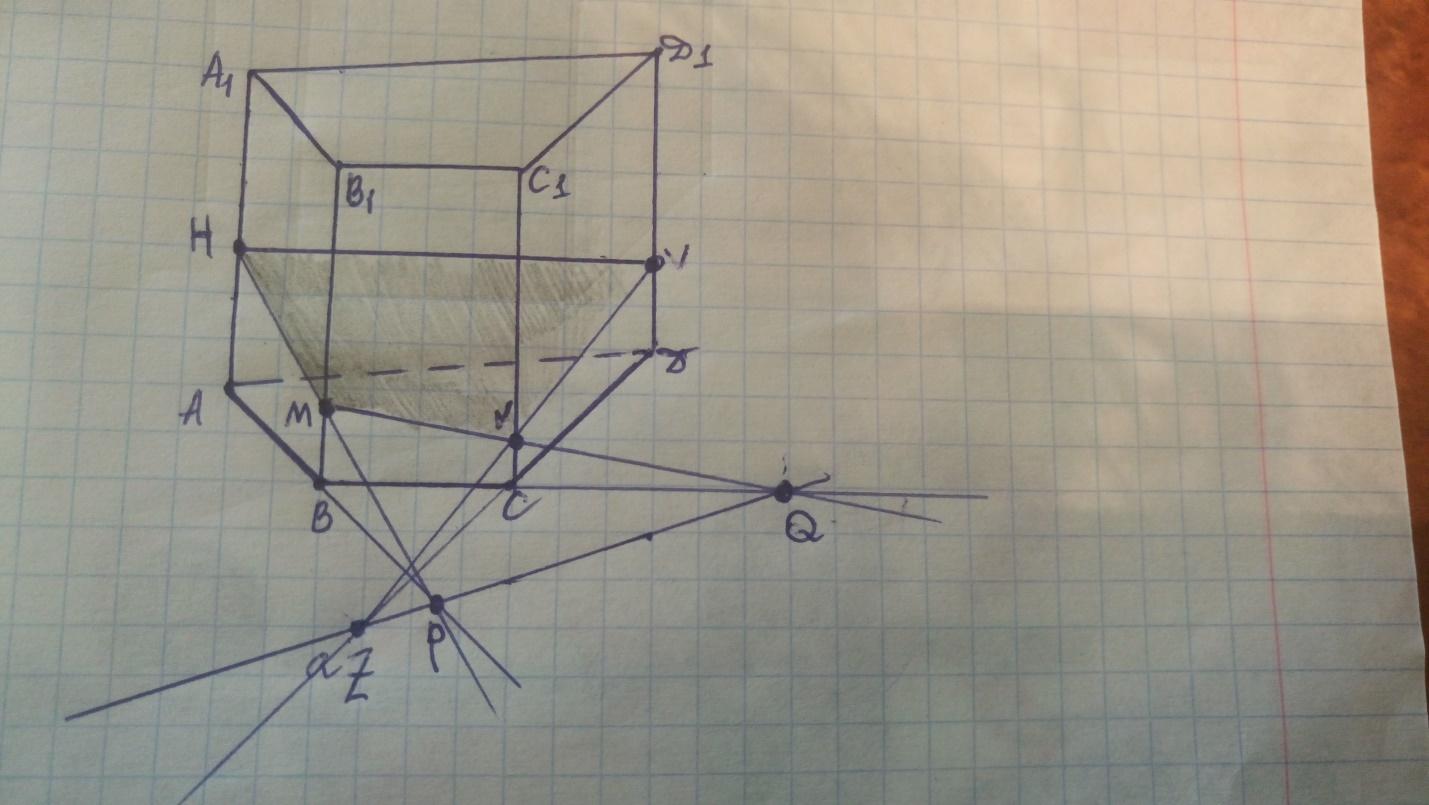
Точки Nи V лежат в одной грани, поэтому проводим прямую NV.

Четырехугольник HVNV – искомое сечение.

Теперь попробуйте выполнить аналогичное задание.

Постройте сечение шестиугольной призмы плоскостью, проходящей через точку на одном из боковых ребер и прямую, лежащую в плоскости нижнего основания.( ученик выходит к доске для решения задачи)

Теперь рассмотрим еще одну задачу.

Построить сечение четырехугольной призмы плоскостью, проходящей через точку А, лежащую в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.

По данному чертежу попробуйте сделать описания хода решения, используя правило №1. (для описания ученик выходит к доске и по чертежу расписывает пошагово ход решения)

Понятно ли вам как строить сечения призмы методом следов?

В чем состоит сложность этого метода именно для вас?

Как вы считаете, всегда ли след плоскости дается в условии?

Так вот, оказывается, что след плоскости в условии дается далеко не всегда. В этом случае этот след необходимо построить, что естественно значительно осложняет решение задачи. Но когда след будет построен, то дальнейшее построение сечения выполняется по общей методике,т.е именно так как мы сегодня строили. Такие задачи мы с вами будем решать на следующем уроке. Не останутся без нашего внимания также и простейшие сечения. например, диагональные. Мы научимся находить площади и периметры таких сечений, а также разберем основные типы задач №16 из бланков профильного уровня ЕГЭ. Но это все на последующих уроках. А сегодня нам было необходимо рассмотреть метод следов. Запишите домашнее задание:

Изучить теоретический материал, котрый мы сегодня рассмотрели.

Построить сечение пятиугольной призмы плоскостью, проходящей через точку М на боковом ребре и прямую лежащую в плоскости нижнего основания.

Построить сечение четырехугольной призмы плоскостью, проходящей через точку в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.( используйте правило №1)

💥 Видео

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Признак параллельности прямой и плоскостиСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Как строить сеченияСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

ЕГЭ 2023 стереометрия 1 вариантСкачать

ЕГЭ стереометрия Вариант 3 задача 13Скачать

Призма Решение задачСкачать

Параллельность прямой к плоскостиСкачать

Сечение Пирамиды Плоскостью Параллельной боковому ребруСкачать

№55. Докажите, что если прямая а пересекает плоскость α, то она пересекает также любуюСкачать

Параллельность прямых. 10 класс.Скачать

Построение призмы высотой 30ммСкачать

ЕГЭ. Математика. Основы стереометрии. ПрактикаСкачать

Построение сечения параллельно прямойСкачать

Ященко. ЕГЭ. Профильная математика. 1 вариант. 2023. 13 задание. GeoGebra.Скачать