Как померить углы в треугольнике

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c» />
a» />
b» />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Видео:Измерение угла с помощью транспортираСкачать

Как померить углы треугольника

Видео:Углы треугольникаСкачать

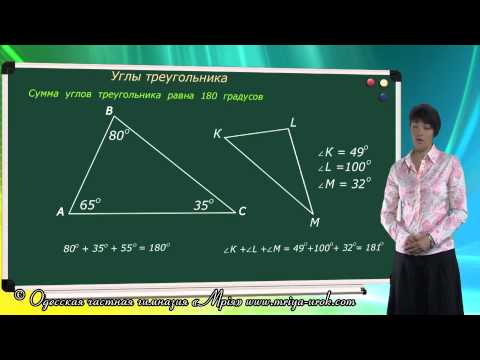
Нахождение углов треугольника по заданным сторонам

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c» />
a» />
b» />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1 ° .

Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

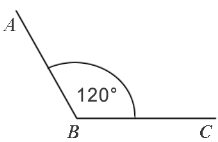
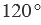
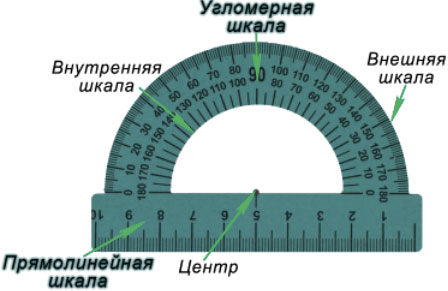
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .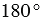

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

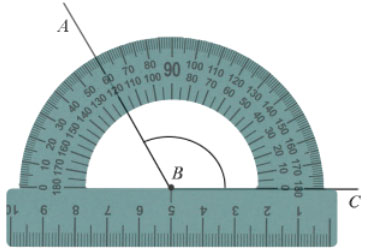
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .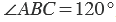

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеетменьшую градусную меру.
• Развернутый угол равен.
• Неразвернутый угол меньше.
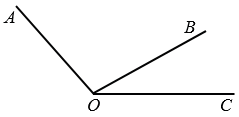
• Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

АОС = АОВ + ВОС.

Виды углов:

1. Острый угол — угол, градусная мера которого меньше 90 ° .

1. Прямой угол — угол, градусная мера которого равна 90 ° .

1. Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 0 .

АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 90 0 .

Поделись с друзьями в социальных сетях:

Видео:Внешний угол треугольникаСкачать

Углы прямоугольного треугольника

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Калькулятор расчёта углов прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α — тангенс угла α
• a — противолежащий катет
• b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Углы прямоугольного треугольника

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Калькулятор расчёта углов прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α — тангенс угла α
• a — противолежащий катет
• b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Видео:Диагностический вариант 4 ЕГЭ по профильной математике. Уровень ЕГЭ 2024Скачать

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

💥 Видео

Построение угла с помощью транспортира. 5 клСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

как пользоваться транспортиром?Скачать

Найдите угол: задача по геометрииСкачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Транспортир. Измерение и построение углов. 5 класс.Скачать

КАК ИЗМЕРИТЬ УГОЛ БЕЗ ТРАНСПОРТИРА С ПОМОЩЬЮ ЛИНЕЙКИ И КАЛЬКУЛЯТОРА | МАТЕМАТИКА ДЛЯ ВСЕХСкачать