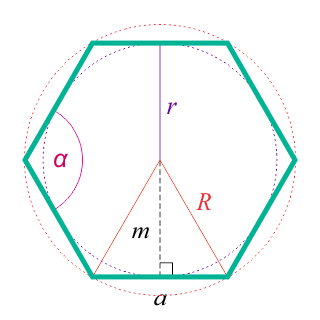
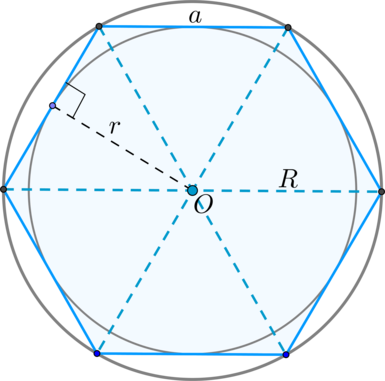
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<>normalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<>normalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Видео:Геометрия - Построение шестиугольникаСкачать

Можно ли вписать окружность в неправильный шестиугольник
| Учебный курс | Решаем задачи по геометрии |
Шестиугольник — это многоугольник, общее количество углов (вершин) которого равно шести. Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами. Чему равна сумма углов выпуклого шестиугольника? Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов. См. теорему о сумме углов многоугольника. При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам. Правильный шестиугольникПравильный шестиугольник — это шестиугольник, все стороны которого равны между собой. Видео:Как построить правильный шестиугольник.Скачать  Свойства правильного шестиугольника
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать  Формулы для правильного шестиугольника(по порядку следования формул)
Видео:Геометрия - Построение восьмиугольникаСкачать  ЗадачаНайти объем цилиндра, вписанного в правильную шестиугольную призму, каждое ребро которой равно t . Решение. Знайти об’єм циліндра, вписаного в правильну шестикутну призму, кожне ребро якої дорівнює t . Рiшення. Видео:Построение правильного шестиугольника при помощи циркуля и линейкиСкачать  Правильный шестиугольник и его свойстваОпределение Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны. Замечание Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ] Пример Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac 4cdot 180^circ=90^circ) ; каждый угол правильного шестиугольника равен (dfrac6cdot 180^circ=120^circ) . Теоремы 1. Около любого правильного многоугольника можно описать окружность, и притом только одну. 2. В любой правильный многоугольник можно вписать окружность, и притом только одну. Следствия 1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах. 2. Центры вписанной и описанной окружности у правильного многоугольника совпадают. Теорема Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfracn\ r&=Rcdot cosdfracn end] Свойства правильного шестиугольника 1. Сторона равна радиусу описанной окружности: (a=R) . 2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника. 3. Все углы правильного шестиугольника равны (120^circ) . 4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt>a^2) . 5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности. 6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями). Замечание В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac) . 🔍 ВидеоПостроение 8 угольника циркулемСкачать  Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать  Как построить шестиугольник вписанный в окружностьСкачать  Вариант 32, №8. Радиус окружности, вписанной в правильный шестиугольник. Длина окружности. ЗадачаСкачать  Вписанная и описанная окружность - от bezbotvyСкачать  Шестиугольник - гексагон за 1 минуту ! Без циркуля и заморочек ! Сможет даже ребёнок .Скачать  ЕГЭ Задание 16 Правильный шестиугольникСкачать  Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать  Как нарисовать правильный шестиугольник | Видеоурок MATHANIMATIONСкачать  111. Окружность, вписанная в правильный многоугольникСкачать  Как начертить три линии под 120 градусов и шестиугольникСкачать  9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать  59. Геометрия на ЕГЭ по математике. Правильный шестиугольник и его свойства.Скачать  9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать  Задание 24 Правильный шестиугольник вписан в окружностьСкачать  |