Постройте сечение пирамиды плоскостью проходящей через прямую am параллельно прямой bd (6 видео)

Задание №1183

Содержание

Условие
Решение
Постройте сечение пирамиды плоскостью проходящей через прямую am параллельно прямой bd
Узнать ещё
Как построить сечение пирамиды
📽️ Видео

Видео:Сечение Пирамиды Плоскостью Параллельной боковому ребруСкачать

Условие

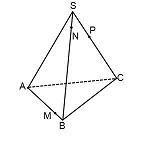
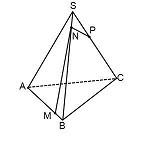
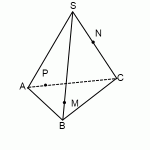
Дана правильная четырёхугольная пирамида KMNPQ со стороной основания MNPQ , равной 6 , и боковым ребром 3sqrt .

а) Постройте сечение пирамиды плоскостью, проходящей через прямую NF параллельно диагонали MP , если точка F — середина ребра MK .

б) Найдите величину угла между плоскостью сечения и плоскостью KMP .

Видео:№3. Как строить сечения пирамидСкачать

Решение

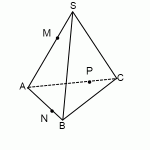
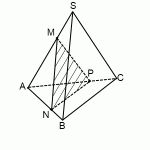
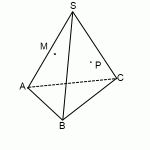
а) Пусть KO — высота пирамиды, F — середина MK ; FE parallel MP ( в плоскости PKM ) . Так как FE — средняя линия triangle PKM, то FE=frac2.

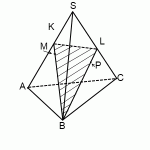
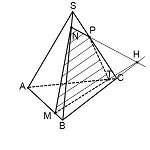
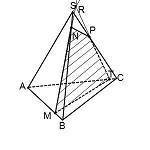
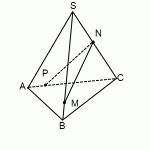
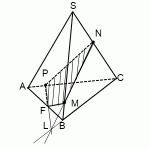
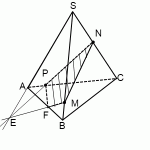
Построим сечение пирамиды плоскостью, проходящей через NF и параллельной MP , то есть плоскостью NFE . L — точка пересечения EF и KO . Так как точки L и N принадлежат искомому сечению и лежат в плоскости KQN , то точка T , полученная как пересечение LN и KQ , является также точкой пересечения искомого сечения и ребра KQ . NETF — искомое сечение.

б) Плоскости NFE и MPK пересекаются по прямой FE . Значит, угол между этими плоскостями равен линейному углу двугранного угла OFEN , построим его: LO perp MP, MP parallel FE, следовательно, LO perp FE; triangle NFE — равнобедренный ( NE=NF как соответствующие медианы равных треугольников KPN и KMN ) , NL — его медиана ( EL=LF, так как PO=OM, а triangle KEF sim triangle KPM ) . Отсюда NL perp FE и angle NLO — искомый.

ON=frac12QN=frac12MNsqrt 2=3sqrt 2.

triangle KON — прямоугольный.

Катет KO по теореме Пифагора равен KO=sqrt .

OL= frac12KO= frac12sqrt= frac12sqrt = frac12sqrt= frac32sqrt = frac32cdot 2sqrt 6= 3sqrt 6.

Видео:Построение сечения параллельно прямойСкачать

Постройте сечение пирамиды плоскостью проходящей через прямую am параллельно прямой bd

Прямая АМ задана. Соединим точку М с вершиной С параллелепипеда и проведем диагональ АС в плоскости его основания.

Диагональ А1С1, лежащей в плоскости, параллельной основанию АВСD, параллельна диагонали АС.

АС ∈ построенной плоскости. Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.

Следовательно, плоскость АМС и прямая А1С1 — параллельны, и АМС — искомая плоскость.

Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Как построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

Построить сечение плоскостью (MNP)

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.

Треугольник MNP — искомое сечение.

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

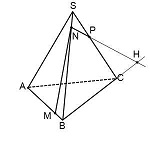
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

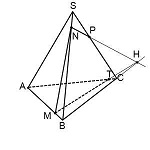
Получим след MT.

T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

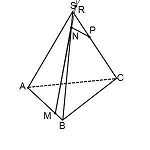
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 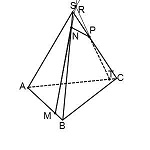которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).