Построить вектор равный вектору 2d

Этот онлайн калькулятор позволит вам очень просто найти проекцию одного вектора на другой вектор.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление проекции вектора на вектор и закрепить пройденный материал.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Калькулятор для вычисления проекции вектора на другой вектор

Инструкция использования калькулятора для вычисления проекции вектора на другой вектор

Ввод даных в калькулятор для вычисления проекции вектора на другой вектор

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления проекции вектора на другой вектор

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Построить разность векторов.Скачать

Теория. Проекция вектора на вектор

Определение Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b. Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Двумерный вектор в C++

Вектор используется для создания динамического массива, и размер вектора можно увеличивать и уменьшать, добавляя и удаляя элементы из вектора. Когда вектор объявляется внутри другого вектора, этот вектор называется 2-мерным вектором, который работает как 2-мерный массив. Двумерный вектор содержит несколько строк, каждая из которых является другим вектором. В этом руководстве показано использование двумерного вектора в C ++.

Синтаксис:

Синтаксис двумерного вектора приведен ниже.

Конкретный тип данных определяется во время объявления вектора. Если размер вектора не определен, вектор называется пустым вектором. Размер вектора можно изменить, используя различные методы или инициализируя вектор.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Пример 1. Создайте двумерный вектор из равного количества столбцов

В следующем примере показан способ объявления двухмерного вектора из трех строк и четырех столбцов, который содержит символьные данные. Здесь значения вектора были определены в момент вектор декларации и вложенную » для » петли используется для печати значения вектора.

using namespace std ;
int main ( )
<
/*
Declare a two-dimensional vector
of characters
*/
vector vector > chrVector
< , , > ;
//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i chrVector. size ( ) ; i ++ )
<
for ( int j = ; j chrVector [ i ] . size ( ) ; j ++ )
cout chrVector [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода.

Видео:Разложение вектора по базису. 9 класс.Скачать

Пример 2: Создайте двумерный вектор с другим количеством столбцов

В следующем примере показан способ объявления двухмерного вектора из четырех строк, где первая строка содержит один столбец, вторая строка содержит два столбца, третья строка содержит три столбца, а четвертая строка содержит четыре столбца. Вектор инициализации с целым данных и распечатаны с помощью вложенной « для » петли.

using namespace std ;

int main ( )
<
/*
Initialize the 2D vector with the
integer number where each row contains different
number of elements
*/
vector vector > intVector
< , , , > ;
//Print the values of the vector using for loop
cout «The values of the vector are: n « ;
for ( vectorrow : intVector )
<
for ( int val : row )
cout val » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода.

Видео:Вычитание векторов. 9 класс.Скачать

Пример 3: Инициализировать двумерный пустой вектор со значением по умолчанию

Способ объявления 2-мерного пустого вектора числа с плавающей запятой и инициализации вектора с числом с плавающей запятой показан в следующем примере. Здесь вложенный цикл for был использован для вставки данных в вектор с помощью функции push_back () и печати значений вектора.

Значение по умолчанию 6.5 было вставлено в вектор путем создания 2 строк и 3 столбцов. Функция size () использовалась для подсчета общего количества строк и столбцов для печати значений вектора.

using namespace std ;

int main ( )
<
//Set the default value
float default_value = 6.5 ;
//Define the outer vector
vector vector > outVect ;

for ( int i = ; i 2 ; i ++ )
<
//Define the inner vector
vectorinVect ;
for ( int j = ; j 3 ; j ++ ) <
//Insert the default value
inVect. push_back ( default_value ) ;
>
//Insert the inner vector to outer vector
outVect. push_back ( inVect ) ;
>

//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i outVect. size ( ) ; i ++ )
<
for ( int j = ; j outVect [ i ] . size ( ) ; j ++ )
cout outVect [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода. Выходные данные показывают содержимое вектора на основе значения по умолчанию и количества строк и столбцов, созданных кодом.

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Пример 4: Инициализировать двумерный пустой вектор, принимая входные значения

В следующем примере показан способ создания двухмерного вектора, получая данные от пользователя. В коде объявлен двумерный пустой вектор целого числа, который будет содержать 2 строки и 3 столбца.

Вложенная » для » петли используется, чтобы принять 6 (2 × 3) целые числа от пользователя и вставить их в вектор с использованием значений индекса. Еще одна вложенная » для » петли была использовано для печати вставленных значений вектора.

using namespace std ;

int main ( )
<
//Define the number of cols
int col = 3 ;
//Define the number of rows
int row = 2 ;
//Initialize an integer variable
int val = ;
//Initialize the empty vector
vector vector > int2DVector ;

//Resize the outer vector
int2DVector. resize ( row ) ;
for ( int i = ; i row ; i ++ )
<
//Resize the inner vector
int2DVector [ i ] . resize ( col ) ;
for ( int j = ; j col ; j ++ )
<
//Take input from the user
cout val ;
//Insert into the vector
int2DVector [ i ] [ j ] = val ;
>
>

//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i int2DVector. size ( ) ; i ++ )
<
for ( int j = ; j int2DVector [ i ] . size ( ) ; j ++ )
cout int2DVector [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода. Выходные данные показывают 6 входных значений и содержимое вектора в зависимости от количества строк и столбцов.

Видео:№758. Начертите два ненулевых коллинеарных вектора а и b так, чтобы | а |≠| b |. Постройте векторыСкачать

Заключение

Двумерный вектор используется в программировании на C ++ для хранения и доступа к данным на основе строк и столбцов. В этом уроке на простых примерах были показаны различные способы создания двумерного вектора. Цель использования двумерного вектора в C ++ будет понятна после прочтения этого руководства.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Видео:Построение проекции вектора на осьСкачать

Понятие вектора

Рассмотрим простейшую задачу. Корабль, двигатель которого развивает скорость 20 км/ч, плывет по течению реки, при этом скорость течения составляет 2 км/ч. Какова скорость корабля относительно берега? Очевидно, в данном случае надо сложить скорость течения и собственную скорость корабля:

20 км/ч + 2 км/ч = 22 км/ч

Теперь посмотрим на почти такую же задачу, которая отличается лишь тем, что корабль плывет уже против течения. Для ее решения скорости уже придется вычитать:

20 км/ч — 2 км/ч = 18 км/ч

Получается, что ответ задачи во многом зависит не только от величин скоростей, но и от их направления. Возможны и более сложные случаи, когда корабль двигается на воде перпендикулярно течению или, например, под углом в 60°. Величины, при операции с которыми необходимо учитывать их направление, называют векторными величинами, или просто векторами.

Помимо скорости к ним относят ускорение, силу, импульс, напряженность магнитного и электрического поля и многие другие величины. Те же величины, для которых нельзя указать направление, называют скалярными величинами. Это масса, температура, плотность и т. п. Для выполнения действий с векторами необходимо разработать общие правила их сложения, вычитания, умножения, которые будут справедливы независимо от физической природы векторных величин. И разработать эти правила помогает как раз геометрия.

Для начала введем понятие вектора. Любой отрезок имеет два конца, которые обычно не отличают друг от друга. Однако если одну из этих точек считать началом отрезка, а другую – собственно концом, то у отрезка появится направление. В таком случае его можно считать вектором.

Часто вектора называют направленными отрезками. Обозначают их с помощью стрелок.

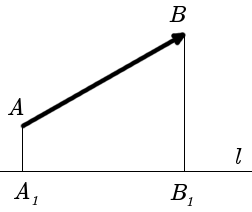
На этом рисунке показан вектор, начало которого находится в точке А, а конец – в точке В. При записи в формулах сначала пишут букву, означающую начало вектора, потом обозначение его конца, а над этими двумя буквами ставят стрелочку:

С практической точки зрения приходится вводить в рассмотрение особый нулевой вектор. У него начало и конец совпадают, то есть он представляет собой всего лишь одну точку:

Нулевой вектор необходим, так как нам необходимо научиться выполнять действия над векторами. Мы знаем, что в обычной алгебре используется число ноль. В векторной же алгебре аналогом нуля является как раз нулевой вектор.

Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке А, а конец в точке В, то длина вектора будет совпадать с длиной отрезка АВ. Обозначают длину с помощью вертикальных скобок:

Естественно, что длина нулевого вектора равна нулю.

Задание. Найдите модуль вектора, изображенного на рисунке:

Решение. Легко выполнить построение, при котором вектор окажется гипотенузой в прямоугольном треугольнике

Тогда длину вектора можно найти по теореме Пифагора:

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Равенство векторов

Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.

На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.

Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.

Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.

Проиллюстрируем эти правила с помощью рисунка:

Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.

Теперь мы можем дать определение равенству векторов.

Задание. Найдите на картинке равные вектора.

Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.

Ответ: a, b и e.

Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А. Докажем важное утверждение:

Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.

Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.

Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:

а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.

б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.

в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.

г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.

Ответ: а) д; б) нет; в) да; г) нет.

Видео:Сложение векторов. 9 класс.Скачать

Сложение векторов

Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.

С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:

Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.

С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:

Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.

Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):

Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:

Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:

Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.

Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.

Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:

а) судно плывет по течению;

б) судно плывет против течения;

в) судно плывет перпендикулярно течению.

Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:

Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:

Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.

Во втором случае вектора уже окажутся противоположно направленными:

Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.

В третьем случае вектора скоростей перпендикулярны:

При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:

Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

Свойства сложения

Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:

Аналогично и при прибавлении к вектору нулевого вектора он не изменится:

Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:

Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что

На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.

Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:

Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:

Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:

Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:

Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой

Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму

Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:

Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.

Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:

В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:

Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Вычитание векторов

Напомним, что в алгебре операция вычитания вводится как операция обратная сложению. То есть если для трех чисел верно соотношение

то разностью чисел с и a как раз окажется b:

Аналогично вычитание понимается и в векторной алгебре. Пусть построены вектора а, b и c так, что

Этот пример показывает, как строить разность двух векторов. На рисунке вектора с и a отложены от одной точки, а вектор b, являющийся их разницей, проведен от конца вычитаемого вектора к концу уменьшаемого вектора.

В данном случае под уменьшаемым вектором понимается тот, который в разнице стоит перед знаком минус, а вычитаемый вектор – тот, который находится уже после этого знака. Например, в записи

Вектор а – уменьшаемый, а вектор b – вычитаемый.

Задание. Постройте в тетради разность векторов, изображенных на рисунке:

Решение. Заметим, что в условии не сказано, какой вектор из какого надо вычитать. Поэтому можно построить сразу два ответа:

Несложно заметить, две получившиеся разности представляют собой противоположно направленные векторы одной длины. Такие векторы называются противоположными.

Очевидно, что если сложить друг с другом два противоположных вектора, то получится нулевой вектор:

Противоположные вектора играют в векторной алгебре такую же роль, как и противоположные числа. С их помощью удобно выполнять вычитание векторов. Напомним, что для обычных чисел справедливо соотношение:

Поэтому операцию вычитания можно заменить операцией сложения, если вместо вычитаемого вектора взять вектор, противоположный ему. Рассмотрим этот способ на примере. Пусть из a надо вычесть b:

На первом шаге надо построить вектор, противоположный b:

Теперь надо просто сложить a и (– b):

В итоге нам удалось построить разность векторов а и b.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Умножение вектора на число

Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:

Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:

Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:

Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.

Задание. На рисунке показаны вектора а и b. Найдите вектора

Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:

Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:

Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:

Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:

Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.

Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:

Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:

Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:

Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:

Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор

Видно, что выражение значительно упростилось.

Видео:№742. Начертите два вектора: а) имеющие равные длины и неколлинеарныеСкачать

Решение задач с помощью векторов

Вектора активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.

Задание. Известно, что С – это середина отрезка АВ. Докажите, что для любой точки О выполняется равенство:

Используя правило треугольника, вектор ОС можно представить в виде двух различных сумм:

Проанализируем выражение в скобках. Вектора АС и ВС коллинеарны, ведь они лежат на одной прямой АВ. При этом они противоположно направлены. Длина у них одинакова, ведь С – середина АВ. Тогда по определению АС и ВС – противоположные вектора, и их сумма равна нулю:

Задание. Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.

Решение. Построим трапецию, обозначим ее вершины и середины оснований:

Здесь ABCD – трапеция, основаниями которой являются отрезки ВС и AD. M и N – их середины. Прямые АВ и CD пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.

Заметим, что ∆ОВС и ∆ОАD подобны. Действительно, у них есть общий ∠ВОС, а ∠ОВС и ∠ОАD одинаковы как односторонние углы при секущей АВ, поэтому треугольники подобны по 1-ому признаку. Обозначим коэффициент подобия буквой k, тогда можно записать, что

Так как отрезки ОА и АВ лежат на одной прямой, то вектора ОА и АВ коллинеарны и притом сонаправлены, поэтому в (1) отрезки можно заменить векторами:

(это соотношение мы доказали в предыдущей, вспомогательной задаче).

Аналогичную формулу можно составить и для второго основания и его середины N:

Полученное нами равенство означает, что вектора ON и ОМ коллинеарны, а значит, лежат на одной прямой (эти вектора не могут лежать на параллельных прямых, так как имеют общую точку О). Тогда получается, что О, M и N лежат на одной прямой, ч. т. д.

🎥 Видео

Координаты вектора в пространстве. 11 класс.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

8 класс, 43 урок, Сумма двух векторовСкачать

Координаты вектора. 9 класс.Скачать