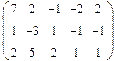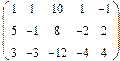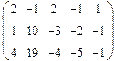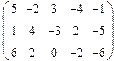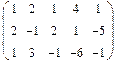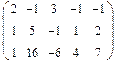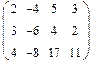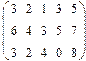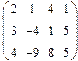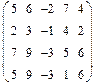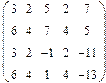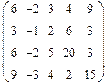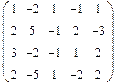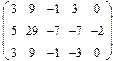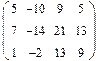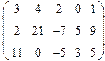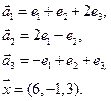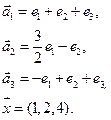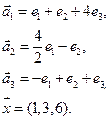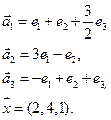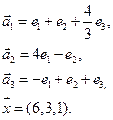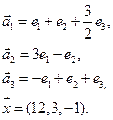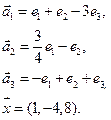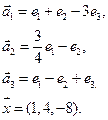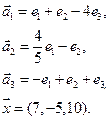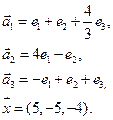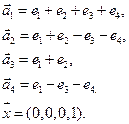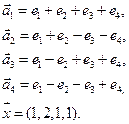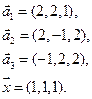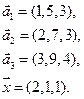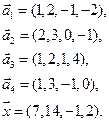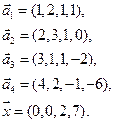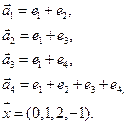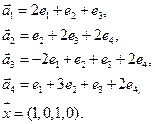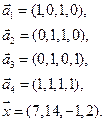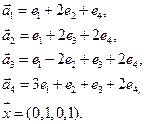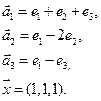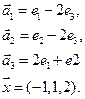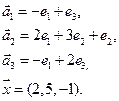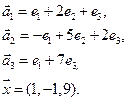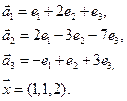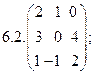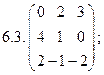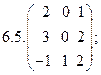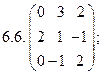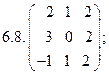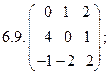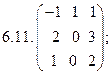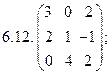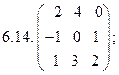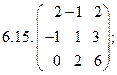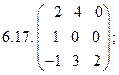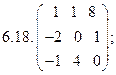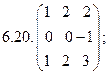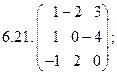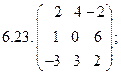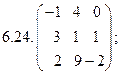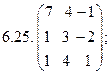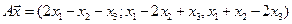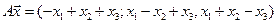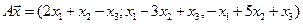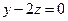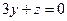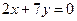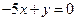Все векторы плоскости каждый из которых лежит на одной из осей

Нет. Например, для многочленов 3 ей степени

и сумма будет многочленом 2 ой степени

3. Образует ли множество радиус-векторов на плоскости, концы которых находятся в первой четверти, линейное пространство (с обычными операциями)?

Нет. Например, умножение элемента данного множества на 3 равен 0? Да.

• 18. Разложить матрицы в сумму симметрической S и кососимметрической А:
  • а) ; б) ; в) .

• 19. Найти:
  • а) ; б) .

• 20. Найти произведение матриц:
  • а) ; б) .

• 21. Найти произведение матриц:
  • а) ; б) ; в) ;

• г) ;
• д) .

• 22. Вычислить произведение матриц:
  • а) ; б) ;

• 23. Вычислить произведения матриц:
  • а) ; б) ;

• в) ;
• г) .

24. Пусть ; ; . Проверить, что . .

25. Даны матрицы:;

• 26. Для заданных пар матриц проверить выполняется ли равенство: :
  • а) ; б) ; в)

. а) да; б) нет; в) нет.

27. Показать, что для матрицы А: :

28. Если , то . Вычислить , если:

• б) ; ;
• в) ; ;
• г) ; .

29. Проверить, что для матриц Паули: , . Справедливы следующие соотношения:

• а) ;
• б) ;

• 30. Показать, что все матрицы перестановочные с матрицей: имеют вид: , где — произвольные числа.
• 31. Найти все матрицы перестановочные с матрицей:
  • а) ; б) ; в) .

32. Для матриц и найти: а) ; б) .

• 33. Выяснить, образует ли данное линейное множество функций на произвольном отрезке [a, b] линейное пространство относительно обычных операций сложения и умножения на число:
  • а) множество С_{[a, b]} функций непрерывных на [a, b];
  • б) множество С 1 _{[a, b]} функций непрерывно дифференцируемых на [a, b];
  • в) множество R_{[a, b]} функций интегрируемых по Риману на [a, b];
  • г) множество функций, ограниченных на [a, b];

• д) множество функций таких, что ;
• е) множество функций неотрицательных на [a, b];
• ж) множество функций таких, что ;
• з) множество функций таких, что ;

• и) множество функций таких, что ;
• к) множество функций, монотонно возрастающих на [a, b];
• л) множество функций, монотонных на [a, b].

а) да; б) да; в) да; г) да; д) нет; е) нет; ж) да; з) нет; и) нет; к) нет; л) нет.

• 34. Выяснить, является ли подпространством данное множество векторов в n-мерном арифметическом пространстве и если является, то найти его размерность:
  • а) множество векторов, у которых первая координата равна 0;
  • б) множество векторов, у которых все координаты равны между

• в) множество векторов сумма координат которых равна 0;
• г) множество векторов сумма координат которых равна 1;
• д) множество векторов плоскости параллельных данной прямой;
• е) множество векторов трехмерного пространства, перпендикулярных

ж) множество векторов плоскости с модулем, не превышающем

з) множество векторов плоскости, образующих угол с данной

а) да, n -1; б) да, 1; в) да, n-1; г) нет; д) да, 1; е) да, 2; ж) нет; з) при = 0 и = /2 — да, 1;

• 35. Является ли линейным подпространством соответствующего линейного пространства каждая из соответствующих совокупностей векторов:
  • а) все векторы n-мерного пространства с целыми координатами;
  • б) все векторы плоскости, каждый из которых лежит на одной из осей

координат Ох или Оу;

• в) все векторы начала и концы которых лежат на данной прямой;
• г) все векторы трехмерного пространства, концы которых не лежат на

а) нет; б) нет; в) да; г) нет.

• 36. Доказать, что следующие системы векторов образуют линейные подпространства, и найти их базис и размерность:
  • а) все n-мерные векторы, у которых первая и последняя координаты

равны между собой;

б) все n-мерные векторы у которых координаты с четными номерами

в) все n-мерные векторы, у которых координаты с четными номерами

равны между собой;

г) все n-мерные векторы вида , где и — лю-

а) n-1; (1, 0, … , 0, 1), (0, 1, 0, … , 0), (0, 0, 1, 0, … , 0), (0, 0, … , 0, 1, 0); б) [(n+1)/2];

• (1, 0, 0, , … , 0), (0, 0, 1, 0, … , 0), (0, 0, 0, 0, 1, 0, … , 0)…; в) [(n+1)/2]+1; (0, 1, 0, 1, 0,1, …),
• (1, 0, 0, … , 0), (0, 0, 1, 0, … , 0), (0, 0, 0, 0, 1, 0,… , 0)…; г) 2; (1, 0, 1, 0, 1, … ),
• (0, 1, 0, 1, 0, 1, 0, … ).
• 37. Выяснить, является ли данное множество квадратных матриц порядка n линейным подпространством в пространстве всех квадратных матриц порядка n и, если является, то найти его размерность:
  • а) множество матриц с нулевой первой строкой;
  • б) множество диагональных матриц;
  • в) множество верхних треугольных матриц;
  • г) множество симметрических матриц;
  • д) множество кососимметрических матриц.

• 38. Установить, являются ли следующие совокупности векторов подпространствами:
  • а) совокупность всех векторов n-мерного пространства (n 2), у которых, по крайней мере, одна из первых двух координат равна нулю;
  • б) совокупность всех векторов n-мерного пространства, у которых первые две координаты и удовлетворяют уравнению: ;
  • в) совокупность всех векторов n-мерного пространства, у которых первые две координаты удовлетворяют уравнению: ;
  • г) все векторы плоскости, концы которых лежать на одной прямой, а начало совпадает с началом координат;
  • д) все векторы, являющиеся линейными комбинациями данных векторов из .

а) нет; б) да; в) нет; г) да, если прямая проходит через начало координат; нет, если прямая не проходит через начало координат; д) да.

• 39. В пространстве полиномов степени не выше 3 является ли подпространством совокупность полиномов, удовлетворяющих условию:
  • а) ; б) .

Если да, то какова его размерность и базис?

а) да; 3; Базис: 1, (х 2 -1), (х 2 -1) х; б) да; 3; Базис: х, х 2 +1, х 3 +2

• 40. В пространстве полиномов степени не выше 3, найти базис и размерность подпространства L полиномов, удовлетворяющих условиям:
  • а) ; б) ;
  • в) ; г) ; д) .

a) dim L = 2; ; б) dim L = 2; ;

в) dim L = 2; ; г) dim L = 3; ;

• д) dim L = 3; .
• 41. В пространстве полиномов степени не выше трех является ли подпространством совокупность полиномов, таких, что . Найти базис и размерность этого пространства.

• 42. Доказать, что при любом данное множество функций образует конечномерное линейное пространство, найти размерность и указать базис этого пространства:
  • а) множество четных полиномов, степени не выше n;
  • б) множество нечетных полиномов, степени не выше n;
  • в) множество тригонометрических полиномов порядка не выше n, т.е.

множество функций вида:

• г) множество четных тригонометрических полиномов порядка не выше n;
• д) множество нечетных тригонометрических полиномов порядка не выше n;
• е) множество функций вида:

где — фиксированное вещественное число.

базис: 1, cosx, sinx, … , cosnx, sinnx; г) n+1; базис: 1, cosx, … , cosnx; д) n; базис:

• 43. Доказать, что данное множество функций образует бесконечномерное линейное пространство:
  • а) множество всех полиномов;
  • б) множество всех тригонометрических полиномов;
  • в) множество функций непрерывных на некотором отрезке.
• 44. Выяснить, будут ли данные векторы линейно зависимы или нет:
  • а) а(1, 3, 1), b(-1, 1, 3), c(-5, -7, 3);
  • б) а(2, -1, -2), b(6, -3, 1);
  • в) а(2, -1, 7, 3), b(1, 4, 11, -2), c(3, -6, 3, 8).

а) да; 2а —b = 0; б) нет; в) да; 3а — b = 0; г) нет; д) да; а + b + с = 0; е) нет.

• 47. Найти размерность и базис линейных подпространств натянутых на системы векторов:
  • а) а₁(1, 0, 0, -1), а₂(2, 1, 1, 0), а₃(1, 1, 1, 1), а₄(1, 2, 3, 4), а₅(0, 1, 2, 3);
  • б) а₁(1, 1, 1, 1, 0), а₂(1, -1, -1, -1, -1), а₃(2, 2, 0, 0, -1), а₄(1, 1, 5, 5, 2),

а) нет; б) да; в) нет; г) да; д) да; е) нет.

• 49. Какова размерность пространства решений уравнения:
  • а) ; б)

• 50. Докажите, что следующие системы функций линейно независимы
• а) sinx, sin2x, sin3x; б) 1, e x , e 2x , e 3x .
• 51. Пусть R + линейное пространство положительных чисел, в котором х ? у ? х . у, а ? х ? х. Доказать, что в R + любые х и у линейно зависимы.
• 52. Выявить линейные зависимости между векторами:
  • а) (1, 3), (3, 2), (-11, 16);
  • б) (1, 1, 1, 1),(1, 1, 1, 3), (3,-5, 7, 2), (1,-7, 5,-2);
  • в) (4, 3, 1), (1, 2, 3), (2, -1, -5);
  • г) (1, 1, 1, 1), (1, 1, 2, 2), (0, 0, 1, 1), (2, 2, 3, 3).

• 53. Векторы e1, e2, … , en в X заданы своими координатами в некотором базисе. Показать, что e1, e2, … , en сами образуют базис и найти координаты вектора х в этом базисе:
  • а) e₁(1, 1, 1), e₂(1, 1, 2), e₃(1, 2, 3), x = (6, 9, 14);
  • б) e₁(2, 1, -3), e₂(3, 2, -5), e₃(1, -1, 1), x = (6, 2, -7);
  • в) e₁(1, 2,-1,-2), e₂(2, 3, 0, -1), e₃(1, 2, 1, 4), e₃(1, 3, -1, 0), x=(7, 14, -1, 2);

а) (1, 2, 3); б) (1, 1, 1); в) (0, 2, 1, 2).

• 54. Найти координаты вектора х в базисе e1, e2, e3: e1(1. 3. 5), e2(6, 3, 2), e3(3, 1, 0), если:
  • а) х(3, 7, 1); б) х(0, 0, 1); в) х(2, 3, 5).

а) (33, -82, 154); б) (-3, 8, -15); в) (-1, 5, -9).

• 55. Найти координаты функции в базисе .
• 56. Линейное пространство полиномов степени не выше n. Показать, что 1, (х-1), (х-1) 2 , … , ), (х-1) n образуют базис этого пространства. Найти в этом базисе координаты многочлена:
  • а) 2 + 3х — 5х 2 + 4х 5 ; б) а₀ + а₁х + … + а_nхn ;

а) (4, 13, 35, 40, 20, 4, 0, 0, …); б) .

57. Найти размерность и базис линейной оболочки системы полиномов: (1 + t)3, t3, 1, t + t2.

3; базис: (1 + t) 3 , t 3 , 1.

58. Доказать, что матрицы образуют базис в пространстве квадратных матриц 2го порядка и найти координаты матрицы в этом базисе.

59. Доказать, что многочлены 2t + t5, t3 — t5, t + t3 образуют базис в пространстве нечетных полиномов степени не выще 5 и найти координаты полинома 5t — t3 + 2t5 в этом базисе.

60. Проверить, что матрицы образуют базис в пространстве квадратных матриц 2го порядка. Матрицу представить, как линейную комбинацию базисных матриц.

• 61. Доказать, что пространство квадратных матриц порядка n является прямой суммой подпространства симметрических матриц и подпространства кососимметрических матриц того же порядка.
• 62. Доказать, что пространство многочленов степени не выше n является прямой суммой четных многочленов степени не выше n и подпространства нечетных многочленов степени не выше n.
• 63. Доказать, что n-мерное линейное пространство является прямой суммой подпространства векторов. Все координаты которых равны между собой и подпространства векторов сумма координат которых равна нулю.
• 64. Доказать, что сумма L двух подпространств P и Q тогда и только тогда будет прямой суммой, когда хотя бы один вектор хL однозначно представляется в виде х = y + z, где уP, zQ.
• 65. Пусть P и Q два линейных подпространства конечномерного линейного пространства V. Доказать, что:
  • а) dim P + dim Q >n = dim VxV, x , xPQ;
  • б) dim P + dim Q = dim PQ + 1, то одно из этих подпространств

содержится в другом.

• 66. Доказать, что для любого линейного подпространства P конечномерного линейного пространства V, существует другое подпространство Q такое, что V = PQ.
• 67. Найти размерность суммы и размерность пересечения линейных подпространств натянутых на системы векторов <a_i> и <b_i>:
  • а) а₁(1, 2, 0, 1), а₂(1, 1, 1, 0); b₁(1, 0, 1, 0), b₂(1, 1, 1, 1);
  • б) а₁(1, 1, 1, 1), а₂(1, -1, 1, -1), а₃(1, 3, 1, 3); b₁(1, 2, 0, 2), b₂(1, 2, 1, 2),

• 69. Найти размерность и базис суммы и пересечения линейных подпространств пространства многочленов степени не выше 3, натянутых на системы многочленов:
• 1 + 2t + t 3 , 1 + t + t 2 , t — t 2 + t 3 и 1 + t 2 , 1 + 3t + t 3 , 3t — t 2 + t 3 .

сумма: 3; базис: <1 + 2t + t 3 , 1 + t 2 , 1 + t + t 2 >; пересечение: 1; базис: <2 + 3t + t 2 + t 3 >.

• 70. а) Доказать, что если в n-мерном комплексном линейном пространстве рассматривать умножение векторов лишь на вещественные числа, то получим 2n-мерное вещественное пространство;
• б) В двумерном комплексном арифметическом пространстве рассматривается операция умножения лишь на вещественные числа. Найти базис в полученном вещественном пространстве и координаты вектора (-3 + 2i, —i) в этом базисе.

• 71. Найти размерность и базис суммы и пересечения линейных подпространств комплексного n-мерного арифметического пространства, натянутых, на системы векторов и :
  • а) n = 3; а₁(1, 2, 3), а₂(1, -2, i), а₃(2, 0, 3 + i); b₁(1, 0, 3i), b₂(1, 4, 3 + i),

• в) 4; базис: а₁, а₂, а₂, b₄; 2; базис: b₁, b₂ .
• 72. Доказать, что множество многочленов степени не выше n с комплексными коэффициентами можно рассматривать и как комплексное линейное пространство и как вещественное линейное пространство. В обоих случаях найти:
  • а) базис и размерность;

• б) координаты многочлена в найденном базисе
• (при n = 2).

a) Комплексное пространство: dim V = n+1, базис: 1, t, t 2 , … t n ; Вещественное пространство:

Вещественное пространство: (1, -2, 3, 1, -3, 0).

• 73. Для заданных матриц А и В найти А+ .В, если:
  • а) ;

• б);
• в) ;
• г) ;
• д) ;
• е) .

• е) .
• 74. Произвести действия с матрицами:
  • а) ;

• б) ;
• в) ;
• г) ;
• д).

• д) .
• 75. Квадратная матрица с комплексными элементами называется эрмитовой, если ; и называется унитарной, если .

Квадратная матрица с вещественными элементами называется самосопряженной, если ; и называется ортогональной, если .

Для следующих матриц установить какими из указанных выше характеристик они обладают:

• в) ; г) ;
• д) ; е) ;

a) ортогональная; б) ортогональна и самосопряженная; в) самосопряженная; г) эрмитова;

• д) эрмитова; е) ортогональная; ж) ортогональная; з) ортогональная.
• 76. Найдите n для указанных ниже пространств, если известно, что эти пространства изоморфны пространству V6:
  • а) для пространства симметричных nхn — матриц с нулевыми диагональными элементами;
  • б) для пространства Р_n полиномов степени не выше n;
  • в) для подпространства многочленов р(х) из Р_n, удовлетворяющих условию: р(0) = 0. a) n = 4; б) n = 5; в) n = 6.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Индивидуальное домашнее задание № 3

1. Является ли линейным подпространством соответствующего век­торного пространства каждая из следующих совокупностей векторов:

1.1. Все векторы п — мерного векторного пространства, координаты которых — целые числа?

1.2. Все векторы плоскости, каждый из которых лежит на одной из осей координат Ох и Оу?

1.3. Все векторы плоскости, концы которых лежат на одной прямой (начало любого вектора предполагается совпадающим с началом координат)?

1.4. Все векторы плоскости, начала и концы которых лежат на данной прямой?

1.5. Все векторы трехмерного пространства, концы которых не лежат на данной прямой?

1.6. Все векторы плоскости, концы которых лежат в первом четверти системы координат?

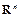
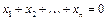
1.7. Все векторы из ,координаты которых удовлетворяют уравнению ?

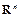
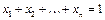
1.8. Все векторы из ,координаты которых удовлетворяют уравнению ?

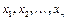
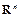
1.9.Все векторы, являющиеся линейными комбинациями данных векторов из ?

1.10. Все п — мерные векторы, у которых первая и последняя координаты равны между собой.

1.11. Все п — мерные векторы, у которых координаты с четными номерами равны нулю.

1.12. Все п — мерные векторы, у которых координаты с четными номерами равны между собой.

1.13. Множество всех симметричных матриц порядка я относительно обычных операций сложения матриц и умножения их на действительное число ?

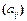
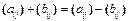
1.14.Множество всех невырожденных матриц порядка п, если сумма их определена так: . а произведение на число -обычным образом ?

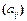
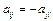
1.15. Множество всех кососимметричных матриц, т.е. матриц удовлетворяющих условию относительно обычных операций сложения матриц и умножения их на число?

1.16.Множество кососимметричных матриц, если их сумма и произведение определены так, как в задаче 1.14?

1.17. Множество решений любой системы однородных линейных уравнений с п переменными ранга 2?

1.18. Множество всех четных функций, заданных на [-1, 1] , если суммой двух функций a=f(t), b=g(t)считается функция f(t)g(t), а произведение на число определяется обычным образом?

1.19. Множество всех нечетных функций, заданных на [-1, 1], если сумма двух функций и произведение на число определены так же, как в задаче 1.18.

1.20.Множество всех дифференцируемых функций с обычными операциями сложения и умножения их на действительное число, если суммой двух функций считается функция f(t)g(t)?

1.21. Множество диагональных квадратных матриц порядка n.

1.22. Множество функций монотонно возрастающих на [а, b].

1.23. Множество функций монотонных на [a, b].

1.24. Множество вырожденных квадратных матриц порядка n.

1.25.Множество функций на [a, b] таких, что f(a)=0.

2. Найти какой-нибудь базис и определить размерность линейного пространства решений однородной системы, основная матрица которой имеет вид:

;

.

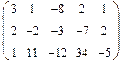
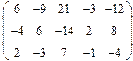
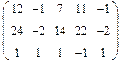
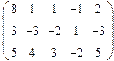
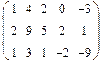
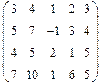
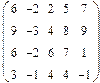
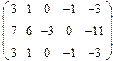
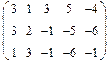
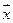
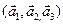
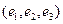
3.Найти координаты вектора в базисе , если он задан в базисе :

4. Пусть 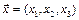. Являются ли линейными следующие преобразования? Если являются, то записать матрицу преобразования.

4.1. ;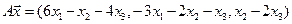

;

.

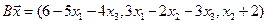
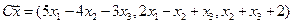
4.2. ;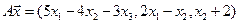

;

.

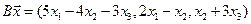
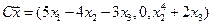
4.3. ;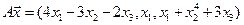

;

.

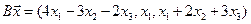
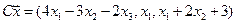
4.4. ;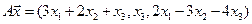

;

.

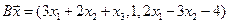
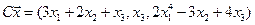
4.5. ;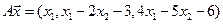

;

.

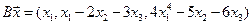
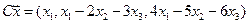
4.6. ;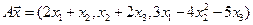

;

.

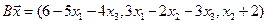
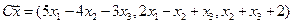
4.7. ;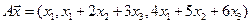

;

.

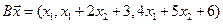
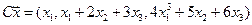
4.8. ;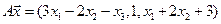

;

.

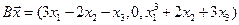
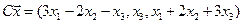
4.9. ;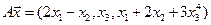

;

.

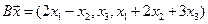
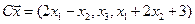
4.10. ;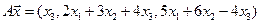

;

.

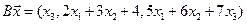
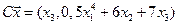
4.11. ;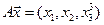

;

.

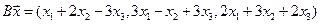
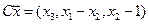
4.12. ;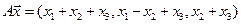

;

.

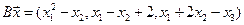
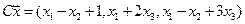
4.13. ;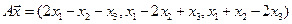

;

.

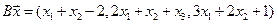
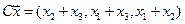
4.14. ;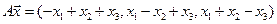

;

.

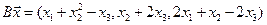
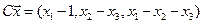
4.15. ;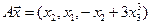

;

.

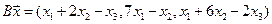
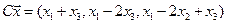
4.16. ;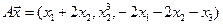

;

.

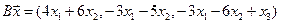
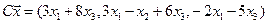
4.17. ;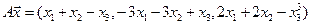

;

.

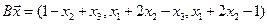
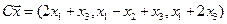
4.18. ;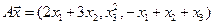

;

.

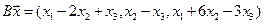
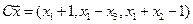
4.19. ;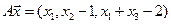

;

.

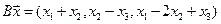
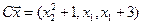
4.20. ;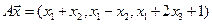

;

.

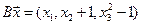
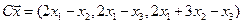
4.21. ;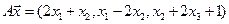

;

.

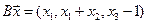
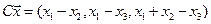
4.22. ;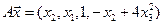

;

.

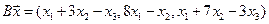
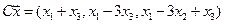
4.23. ;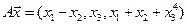

;

.

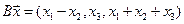
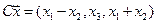
4.24. ;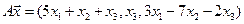

;

.

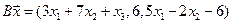
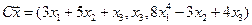
4.25. ;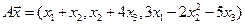

;

.

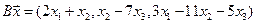
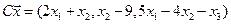
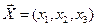
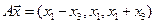
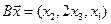
5. Пусть , , . Найти

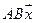
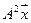
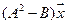
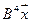
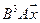
5.1. ; 5.2. ; 5.3. ; 5.4. ; 5.5. ;

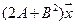
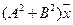
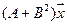
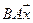
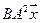
5.6. ; 5.7. ; 5.8. ; 5.9. ; 5.10. ;

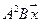
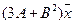
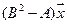
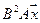
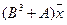
5.11. ; 5.12. ; 5.13. ; 5.14. ; 5.15. ;

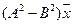
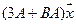
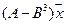
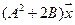
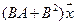
5.16. ; 5.17. ; 5.18. ; 5.19. ; 5.20. ;

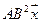
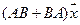
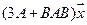
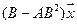
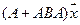
5.21. ; 5.22. ; 5.23. ; 5.24. ; 5.25. .

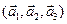
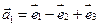
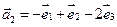
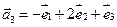
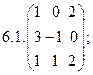
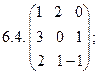
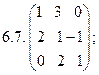
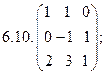
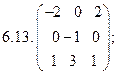
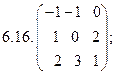
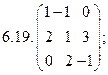
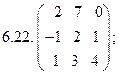
6.Найти матрицу линейного оператора в базисе , где , , , если она задана в базисе :

7. Найти матрицу, область значений и ядро линейного оператора А. Определить ранг и дефект:

7.1. .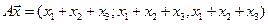

7.2.

7.3.

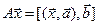
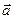
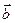
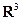
7.4. , где и — заданные векторы в .

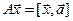
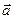
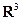
7.5. , где — заданный вектор в .

7.6. — многочлены степени .

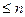
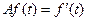
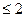
7.7. — многочлены степени , А — оператор дифференцирования.

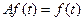
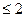
7.8. — многочлены степени .

7.9. А — зеркальное отражение относительно плоскости .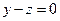

7.10. А — зеркальное отражение относительно плоскости .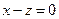

7.11. А — зеркальное отражение относительно плоскости .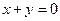

7.12. А — зеркальное отражение относительно плоскости .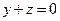

7.13. А — зеркальное отражение относительно плоскости

7.14. А — зеркальное отражение относительно плоскости .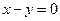

7.15. А — зеркальное отражение относительно плоскости .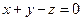

7.16. А — проектирование на плоскость .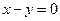

7.17. А — проектирование на плоскость .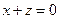

7.18. А — проектирование на плоскость .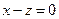

7.19.А — проектирование на плоскость .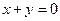

7.20.А — проектирование на плоскость .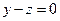

7.21.

7.22.А – зеркальное отражение относительно плоскости

7.23.А – зеркальное отражение относительно плоскости

7.24. А – проектирование на плоскость

7.25. А – проектирование на плоскость

8. Найти собственные векторы линейного оператора. Привести матрицу линейного оператора к нормальному виду (форме Жордана).

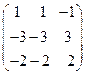
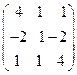
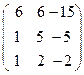
8.1. ; 8.2. ; 8.3. ;

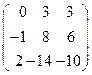
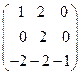
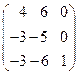
8.4. ; 8.5. ; 8.6. ;

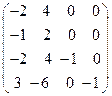
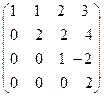
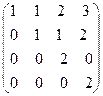
8.7. ; 8.8. ; 8.9. ;

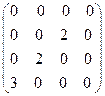
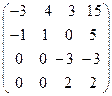
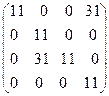
8.10. ; 8.11. ; 8.12. ;

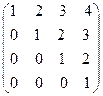
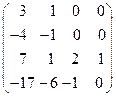
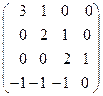
8.13. ; 8.14. ; 8.15. ;

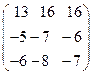
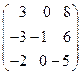
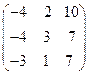
8.16. ; 8.17. ; 8.18. ;

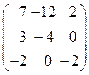
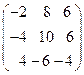
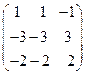
8.19. ; 8.20. ; 8.21. ;

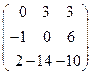
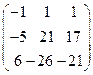
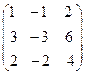
8.22. ; 8.23. ; 8.24. ;

8.25. .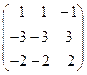

5.4. Примерные варианты 20 — минутной самостоятельной работы по теме «Линейные преобразования»

Вариант № 1

1. Матрица 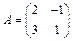является матрицей перехода от базиса В к базису С. Найти координаты вектора в В, если его координаты в С равны (-1,2).

2. Дать определение инвариантного подпространства линейного оператора .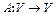

3. Матрица оператора имеет вид: 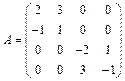. Указать инвариантные подпространства этого оператора.

4. Записать характеристическое уравнение линейного оператора с матрицей 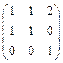. Найти его корни.

Вариант № 2

1. Дать определение линейного отображения .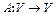

2. Дать определение матрицы линейного оператора.

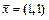
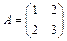
3. Проверить, является ли вектор собственным вектором линейного оператора с матрицей

.

4. Приводится ли матрица к диагональному виду ?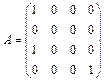

5.5 Примерные варианты контрольной работы по линейной алгебре

Вариант № 1

1. Не вычисляя канонического базиса, найти жорданову форму следующей матрицы

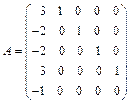2.Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на векторы .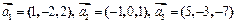

3.Привести к каноническому виду квадратичную форму .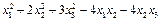

Вариант №2

1. Не вычисляя канонического базиса, найти жорданову форму следующей матрицы

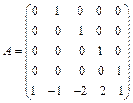2.Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на векторы .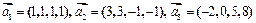

3.Привести к каноническому виду квадратичную форму .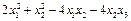

6. ПРОГРАММА ЭКЗАМЕНА ПО КУРСУ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА»

1. Понятие вектора в геометрии. Линейные операции над векторами и их свойства.

Понятие линейного векторного пространства. Примеры линейных векторных пространств. Пространство .

2. Понятие системы линейных уравнений и ее решения. Совместные и несовместные системы. Определенные и неопределенные системы. Элементарные преобразования системы. Равносильные системы.

3. Правило Жордана-Гаусса исключения переменной из всех уравнений системы кроме одного. Приведение системы к единичному базису. Решение системы линейных уравнений.

4. Однородная система линейных уравнений и свойства ее решений. Связь решений неоднородной системы и соответствующей ей однородной.

5. Линейно зависимые и линейно независимые системы векторов. Необходимое и достаточное условие линейной зависимости векторов. Примеры.

6. Свойства линейно зависимых и линейно независимых систем векторов. Линейная зависимость векторов в .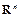

7. Понятие базиса системы векторов. Теорема о двух различных базисах одной и той же системы векторов. Координаты вектора в данном базисе.

8. Ранг системы векторов, его свойства. Размерность векторного пространства.

9. Понятие ранга матрицы. Решение задач по отысканию ранга матрицы.

10. Операции над матрицами, их свойства. Размерность пространства однотипных матриц размера .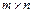

11. Обратная матрица. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы.

12. Понятие определителя квадратной матрицы. Минор и алгебраическое дополнение. Правило Лапласа разложения определителя по элементам какой-либо строки (столбца).

13. Свойства определителей, методы их вычисления.

14. Вычисление обратной матрицы с помощью алгебраических дополнений ее элементов. Правило Крамера решения системы линейных уравнений.

15. Скалярное произведение векторов, его свойства и приложения в геометрии и физике.

16. Векторное произведение векторов, его геометрический смысл, свойства, приложения.

17. Смешанное произведение векторов, его геометрический смысл, свойства, приложения. Двойное векторное произведение.

18. Понятие аффинной и прямоугольной декартовой системы координат на плоскости и в пространстве. Координаты точки. Геометрический смысл координат точки в прямоугольной декартовой системе координат.

19. Полярная система координат, ее связь с прямоугольной декартовой. Сферические и цилиндрические координаты.

20. Различные уравнения прямой линии на плоскости и в пространстве: параметрические уравнения по точке и направляющему вектору, по двум точкам, канонические уравнения.

21. Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов в прямоугольной декартовой системе координат. Уравнение прямой по точке и угловому коэффициенту.

22. Уравнение прямой в отрезках. Уравнение прямой по точке и нормальному вектору в прямоугольной декартовой системе координат.

23. Взаимное расположение двух прямых на плоскости. Расположение прямойотносительно осей координат.

24. Угол между прямыми. Расстояние от точки до прямой на плоскости.

25. Различные уравнения плоскости: параметрические по точке и двум направляющим векторам, трем точкам, общее уравнение плоскости.

26. Взаимное расположение двух и трех плоскостей. Прямая как пересечение двух плоскостей.

27. Взаимное расположение прямой и плоскости, двух прямых в пространстве.

28. Уравнение плоскости по точке и нормальному вектору. Расстояние от точки до плоскости в пространстве.

29. Расстояние от точки до прямой в пространстве. Угол между плоскостями.

30. Эллипс, его каноническое уравнение и свойства.

31. Гипербола, ее каноническое уравнение, свойства. Асимптоты гиперболы.

32. Парабола, ее каноническое уравнение и свойства.

33. Поверхности вращения: эллипсоид, гиперболоиды, параболоид.

34. Канонические уравнения поверхности второго порядка и их исследование методом сечений.

35. Конические и цилиндрические поверхности.

36. Подпространства линейного векторного пространства, их пересечение и сумма. Примеры. Теорема о размерности суммы двух подпространств.

37. Прямая сумма подпространств. Линейная оболочка системы векторов.

38. Понятие базиса векторного пространства и координат вектора. Преобразование координат векторов при переходе к новому базису.

39. Понятие линейного оператора. Примеры линейных операторов. Простейшие свойства. Матрица линейного оператора.

40. Арифметические операции над линейными операторами и их свойства.

41. Изменение матрицы линейного оператора при переходе к новому базису.

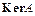
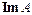
42. Ядро и образ линейного оператора. Ранг и дефект. Теорема о взаимосвязи между размерностями подпространств и .

43. Инвариантные подпространства линейного оператора. Разложение пространства в прямую сумму инвариантных относительно некоторого оператора подпространств.

44. Понятие собственного вектора линейного оператора. Характеристический многочлен и собственные значения линейного оператора.

45. Свойства собственных векторов линейного оператора. Приведение матрицы линейного оператора к диагональному виду. Жорданова нормальная форма матрицы линейного оператора (понятие).

46. Понятие евклидова пространства над полем вещественных чисел (комплексных чисел). Примеры евклидовых пространств. Длина векторов угол между двумя векторами.

47. Ортогональный базис евклидова пространства. Теорема о линейной независимости попарно ортогональных векторов данной системы. Процесс ортогонализации построения ортогональных векторов.

48. Ортогональные подпространства евклидова пространства. Необходимое и достаточное условие ортогональности 2-х подпространств. Теорема о пересечении двух взаимно ортогональных подпространств.

49. Ортогональное дополнение подпространства 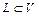, его построение. Ортогональная проекция вектора на подпространство.

50. Понятие билинейной формы. Матрица билинейной формы, ее изменение при переходе к новому базису. Ранг билинейной формы.

51. Симметрическая и кососимметрическая билинейные формы. Необходимое и достаточное условие симметричности (кососимметричности). Теорема о представлении любой билинейной формы в виде суммы симметрической и кососимметрической билинейных форм.

52. Квадратичная форма, ее матрица. Приведение квадратичной формы к сумме квадратов (теорема).

53. Каноническая форма квадратичной формы. Закон инерции квадратичных форм. Положительно- и отрицательно-определенные квадратичные формы, критерий Сильвестра.

54. Билинейные и квадратичные формы в комплексном евклидовом пространстве. Изменение матрицы билинейной формы при переходе к новому базису. Эрмитовы билинейные и квадратичные формы.

55. Понятие оператора, сопряженного к данному. Матрица сопряженного оператора. Свойства операции сопряжения.

56. Самосопряженный оператор, его матрица, свойства.

57. Каноническая форма матрицы самосопряженного оператора, в евклидовом пространстве.

58. Унитарный оператор, его свойства. Канонический вид матрицы.

59. Ортогональный оператор, его свойства и матрица.

60. Ортогональные операторы, действующие в одномерном и двумерном евклидовых пространствах

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

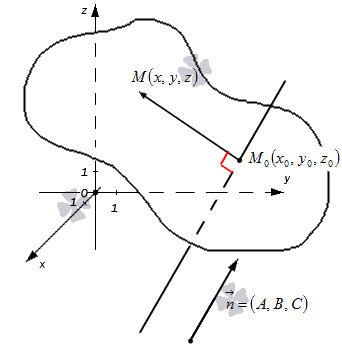
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

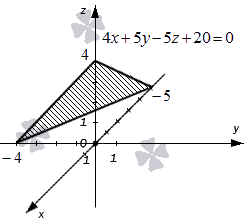
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

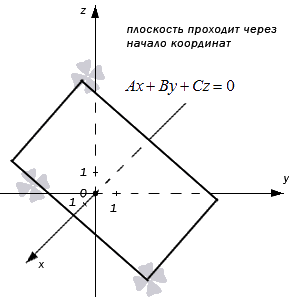
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

💥 Видео

Телекинокурс. Высшая математика. Лекции 31-32. Векторная алгебра. Часть 01 (1973)Скачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Найдите разложение вектора по векторам (базису)Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Как разложить вектор по базису - bezbotvyСкачать

Профильный ЕГЭ 2024. Векторы. Координатная плоскость. Задача 2Скачать