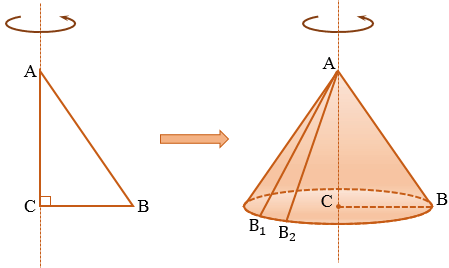
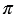Если вращать треугольник получится (2 видео)

Конус

Конус — это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.

Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.

Прямая АС — ось косинуса.

Отрезок АС — высота конуса.

Основание конуса — круг, образованный при вращении катета ВС.

Коническая поверхность (или боковая поверхность конуса) — поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.

Образующие конуса — отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ₁ и АВ₂).

Содержание

Определение
Объем конуса
Доказательство
Площадь боковой поверхности конуса
Фигуры вращения
Описание презентации по отдельным слайдам:
Охрана труда
Библиотечно-библиографические и информационные знания в педагогическом процессе
Охрана труда
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
Презентация на тему: Фигуры вращения
🎦 Видео

Определение

Конус — это тело, ограниченное кругом и конической поверхностью.

Объем конуса

Объем конуса равен одной трети произведения площади основания на высоту.

Доказательство

Дано: конус с площадью основания S, высотой h и объемом V.

Доказать: V = 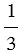Sh.

Доказательство:

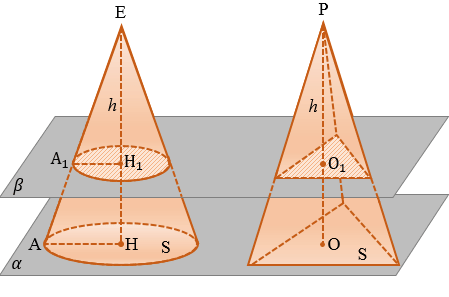
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, «стоящие» на одной плоскости .

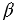
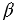
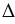
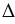
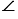
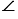
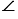
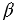
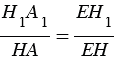
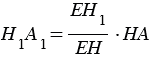
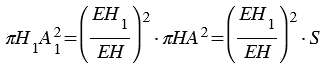
Проведем секущую плоскость , параллельную плоскости и пересекающую высоты ЕН и РО в точках Н₁ и О₁ соответственно. В сечении конуса плоскостью получится круг радиуса Н₁А₁.

ЕН₁А₁ подобен ЕНА по двум углам (Е — общий, ЕН₁А₁ = ЕНА = 90 0 , т.к. в противном случае прямые НА и Н₁А₁, а значит, и плоскости и пересекались бы, что противоречит условию). Поэтому , откуда и площадь сечения конуса равна .

Площадь сечения пирамиды равна 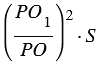. По условию ЕН = РО = h, значит, ЕН₁ = РО₁ (т.к. ЕН₁ = h — НН₁ и РО₁ = h — ОО₁, параллельные плоскости отсекают одинаковые отрезки НН₁ и ОО₁ от отрезков ЕН и РО, т.е. НН₁ = ОО₁).

Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 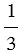Sh. Что и требовалось доказать.

Площадь боковой поверхности конуса

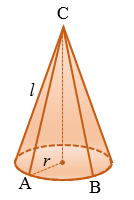
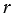
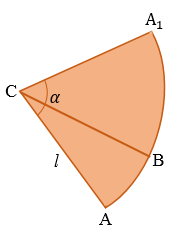
Рассмотрим конус с радиусом основания и образующей .

Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.

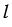
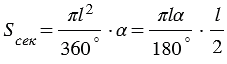
Радиус этого сектора равен образующей конуса, т.е. равен , а длина дуги сектора равна длине окружности основания конуса, т.е. равна 2, — градусная мера дуги сектора, тогда площадь данного сектора: . (1)

Длина дуги окружности с градусной мерой и радиусом равна . С другой стороны, длина этой дуги равна 2, поэтому учитывая (1), получим: .

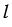
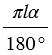
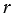
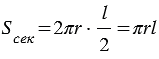
Площадь боковой поверхности конуса равна площади ее развертки, т.е.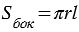

Поделись с друзьями в социальных сетях:

Видео:Построение натуральной величины треугольника методом вращенияСкачать

Фигуры вращения

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ПОВОРОТ
Пусть теперь в пространстве задана прямая a и точка A, не принадлежащая этой прямой. Через точку A проведем плоскость α, перпендикулярную прямой a, и точку пересечения a и  обозначим O. Говорят, что точка A’ пространства получается из точки A поворотом вокруг прямой a на угол φ, если в плоскости α точка A’ получается из точки A поворотом вокруг центра O на угол φ.
Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол φ называется поворотом, или вращением. Прямая a при этом называется осью вращения.

ФИГУРЫ ВРАЩЕНИЯ
Говорят,что фигура Ф в пространстве получена вращением фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.
При вращении точки A вокруг прямой a получается окружность.
Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.

ФИГУРЫ ВРАЩЕНИЯ
Цилиндр получается вращением прямоугольника вокруг одной из его сторон.
Конус получается вращением прямоугольного треугольника вокруг одного из его катетов.
Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу.

ФИГУРЫ ВРАЩЕНИЯ
Если окружность вращать вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек, то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик.
При вращении эллипса вокруг его оси получается поверхность, называемая эллипсоидом вращения.

ФИГУРЫ ВРАЩЕНИЯ
При вращении параболы вокруг ее оси получается поверхность, называемая параболоидом вращения.
При вращении гиперболы вокруг ее оси получается поверхность, называемая гиперболоидом вращения.

ФИГУРЫ ВРАЩЕНИЯ
Если прямая параллельна оси, то при вращении получается фигура, называемая цилиндрической поверхностью. Если прямая пересекает ось, то при вращении получается фигура, называемая конической поверхностью.

ГИПЕРБОЛОИД ВРАЩЕНИЯ
Теорема. При вращении прямой, скрещивающейся с осью вращения, получается гиперболоид вращения.

ВРАЩЕНИЕ КУБА 1
При вращении куба вокруг диагонали получается фигура, поверхность которой состоит из боковых поверхностей двух конусов и поверхности гиперболоида вращения.

ВРАЩЕНИЕ КУБА 2
При вращении куба вокруг прямой, соединяющей середины двух противоположных ребер, получается фигура, поверхность которой состоит из двух кругов и двух поверхностей гиперболоидов вращения.

Упражнение 1
Какая фигура получается при вращении отрезка OA вокруг прямой, проходящей через точку O и перпендикулярной OA?
Ответ: Круг.

Упражнение 2
Назовите прямые, при вращении вокруг которых данного прямоугольника получается цилиндр.
Ответ: Прямые, пересекающие прямоугольник по отрезку, параллельному его стороне.

Упражнение 3
Какая фигура получается при вращении равнобедренного треугольника вокруг прямой, содержащей высоту, опущенной на основание этого треугольника?
Ответ: Конус.

Упражнение 4
Какая фигура получается при вращении полукруга вокруг прямой, содержащей диаметр?
Ответ: Круг.

Упражнение 5
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей его катет?
Ответ: Конус.

Упражнение 6
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, и проходящей через вершину острого угла перпендикулярно катету?
Ответ: Цилиндр, из которого вырезан конус.

Упражнение 7
Какая фигура получается вращением равнобедренного прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, перпендикулярной гипотенузе и проходящей через вершину острого угла.
Ответ: Усеченный конус, из которого вырезан конус.

Упражнение 8
Какая фигура получается вращением остроугольного треугольника вокруг прямой, содержащей его сторону?
Ответ: Фигура, состоящая из двух конусов с общим основанием.

Упражнение 9
Ответ: Усечённый конус с вырезанным внутри конусом.
Какая фигура получается вращением остроугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через его вершину перпендикулярно стороне?

Упражнение 10
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, содержащей его сторону, прилегающую к тупому углу?
Ответ: Фигура, полученная из конуса, вырезанием из него другого конуса.

Упражнение 11
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через вершину тупого угла параллельно противолежащей стороне?
Ответ: Цилиндр с вырезанными внутри двумя конусами, имеющими общую вершину.

Упражнение 12
Какая фигура получается вращением прямоугольника вокруг прямой, лежащей в плоскости этого прямоугольника, параллельной его стороне, и не имеющей с ним общих точек?
Ответ: Фигура, полученная из цилиндра, вырезанием из него другого цилиндра.

Упражнение 13
Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее её основание?
Ответ: Цилинд с вырезанными внутри двумя конусами.

Упражнение 14
Какая фигура получается вращением трапеции вокруг прямой, содержащей большее её основание?
Ответ: Цилиндр, на основания которого поставлены конусы.

Упражнение 15
Какая фигура получается при вращении куба вокруг прямой, соединяющей центры противоположных граней.
Ответ: Цилиндр.

Упражнение 16
Какая фигура получится при вращении правильной n-угольной призмы вокруг прямой, проходящей через центры ее оснований?
Ответ: Цилиндр.

Упражнение 17
Какая фигура получается при вращении правильной n-угольной пирамиды вокруг прямой, содержащей ее высоту?
Ответ: Конус.

Упражнение 18
Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей середины скрещивающихся ребер?
Ответ: Фигура, ограниченная двумя кругами и гиперболоидом вращения.

Упражнение 19
Какая фигура получается при вращении октаэдра вокруг прямой, проходящей через противоположные вершины?
Ответ: Фигура, состоящая из двух конусов с общим основанием.

Упражнение 20
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Показательной функции.

Упражнение 21
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Синусоиды.

Упражнение 22
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ:

Упражнение 23
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ:

Упражнение 24
Тетраэдр повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является объединением и пересечением исходного тетраэдра и повернутого?
Ответ: Звезда Кеплера, октаэдр.

Упражнение 25
Куб повернут вокруг прямой, соединяющей центры противоположных граней, на угол 45о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Правильная 8-я призма.

Упражнение 26
Куб повернут вокруг диагонали на угол 60о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Правильная 6-я бипирамида.

Упражнение 27
Куб повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является общей частью исходного куба и повернутого?
Ответ: Две правильные 4-е пирамиды, поставленные на основания правильной 4-ой призмы.

Упражнение 28
Октаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол 45о. Какая фигура является общей частью исходного октаэдра и повернутого?
Ответ: Правильная 8-я бипирамида.

Упражнение 29
Октаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на угол 60о. Какая фигура является общей частью исходного октаэдра и повернутого?
Ответ: Правильная усеченная 6-я бипирамида.

Курс повышения квалификации

Охрана труда

Сейчас обучается 98 человек из 44 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Сейчас обучается 349 человек из 64 регионов

Курс профессиональной переподготовки

Охрана труда

Сейчас обучается 216 человек из 53 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 535 115 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

14.12.2020
99
0

13.12.2020
133
0

07.12.2020
114
1

06.10.2020
83
0

29.09.2020
88
0

12.09.2020
71
0

09.09.2020
133
0

07.09.2020
162
0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

05.12.2020 848
PPTX 1.2 мбайт
5 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Садртдинова Рауфина Гаделхановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 1 год и 1 месяц
Подписчики: 0
Всего просмотров: 28930
Всего материалов: 250

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

В Свердловской области школьников со 2 по 8 класс и студентов переводят на удаленку

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В ЕГЭ обновили задания по математике

Время чтения: 2 минуты

Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вращение вокруг проецирующей прямой и прямой уровняСкачать

Презентация на тему: Фигуры вращения

ПОВОРОТ Пусть теперь в пространстве задана прямая a и точка A, не принадлежащая этой прямой. Через точку A проведем плоскость α, перпендикулярную прямой a, и точку пересечения a и обозначим O. Говорят, что точка A’ пространства получается из точки A поворотом вокруг прямой a на угол φ, если в плоскости α точка A’ получается из точки A поворотом вокруг центра O на угол φ.Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол φ называется поворотом, или вращением. Прямая a при этом называется осью вращения.

ФИГУРЫ ВРАЩЕНИЯ Говорят,что фигура Ф в пространстве получена вращением фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.

ФИГУРЫ ВРАЩЕНИЯ Цилиндр получается вращением прямоугольника вокруг одной из его сторон. Конус получается вращением прямоугольного треугольника вокруг одного из его катетов. Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу.

ФИГУРЫ ВРАЩЕНИЯ Если окружность вращать вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек, то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик.При вращении эллипса вокруг его оси получается поверхность, называемая эллипсоидом вращения.

ФИГУРЫ ВРАЩЕНИЯ При вращении параболы вокруг ее оси получается поверхность, называемая параболоидом вращения.При вращении гиперболы вокруг ее оси получается поверхность, называемая гиперболоидом вращения.

ФИГУРЫ ВРАЩЕНИЯ Если прямая параллельна оси, то при вращении получается фигура, называемая цилиндрической поверхностью. Если прямая пересекает ось, то при вращении получается фигура, называемая конической поверхностью.

ГИПЕРБОЛОИД ВРАЩЕНИЯ Теорема. При вращении прямой, скрещивающейся с осью вращения, получается гиперболоид вращения.

ВРАЩЕНИЕ КУБА 1 При вращении куба вокруг диагонали получается фигура, поверхность которой состоит из боковых поверхностей двух конусов и поверхности гиперболоида вращения.

ВРАЩЕНИЕ КУБА 2 При вращении куба вокруг прямой, соединяющей середины двух противоположных ребер, получается фигура, поверхность которой состоит из двух кругов и двух поверхностей гиперболоидов вращения.

Упражнение 1Какая фигура получается при вращении отрезка OA вокруг прямой, проходящей через точку O и перпендикулярной OA?

Упражнение 2Назовите прямые, при вращении вокруг которых данного прямоугольника получается цилиндр.

Упражнение 3Какая фигура получается при вращении равнобедренного треугольника вокруг прямой, содержащей высоту, опущенной на основание этого треугольника?

Упражнение 4Какая фигура получается при вращении полукруга вокруг прямой, содержащей диаметр?

Упражнение 5Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей его катет?

Упражнение 6Какая фигура получается вращением прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, и проходящей через вершину острого угла перпендикулярно катету?

Упражнение 7Какая фигура получается вращением равнобедренного прямоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника, перпендикулярной гипотенузе и проходящей через вершину острого угла.

Упражнение 8Какая фигура получается вращением остроугольного треугольника вокруг прямой, содержащей его сторону?

Упражнение 9Какая фигура получается вращением остроугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через его вершину перпендикулярно стороне?

Упражнение 10Какая фигура получается вращением тупоугольного треугольника вокруг прямой, содержащей его сторону, прилегающую к тупому углу?

Упражнение 11Какая фигура получается вращением тупоугольного треугольника вокруг прямой, лежащей в плоскости этого треугольника и проходящей через вершину тупого угла параллельно противолежащей стороне?

Упражнение 12Какая фигура получается вращением прямоугольника вокруг прямой, лежащей в плоскости этого прямоугольника, параллельной его стороне, и не имеющей с ним общих точек?Ответ: Фигура, полученная из цилиндра, вырезанием из него другого цилиндра.

Упражнение 13Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее её основание?

Упражнение 14Какая фигура получается вращением трапеции вокруг прямой, содержащей большее её основание?

Упражнение 15Какая фигура получается при вращении куба вокруг прямой, соединяющей центры противоположных граней.

Упражнение 16Какая фигура получится при вращении правильной n-угольной призмы вокруг прямой, проходящей через центры ее оснований?

Упражнение 17Какая фигура получается при вращении правильной n-угольной пирамиды вокруг прямой, содержащей ее высоту?

Упражнение 18Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей середины скрещивающихся ребер?Ответ: Фигура, ограниченная двумя кругами и гиперболоидом вращения.

Упражнение 19Какая фигура получается при вращении октаэдра вокруг прямой, проходящей через противоположные вершины?Ответ: Фигура, состоящая из двух конусов с общим основанием.

Упражнение 20Вращением графика какой функции получена поверхность, изображенная на рисунке?

Упражнение 21Вращением графика какой функции получена поверхность, изображенная на рисунке?

Упражнение 22Вращением графика какой функции получена поверхность, изображенная на рисунке?

Упражнение 23Вращением графика какой функции получена поверхность, изображенная на рисунке?

Упражнение 24Тетраэдр повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является объединением и пересечением исходного тетраэдра и повернутого?

Упражнение 25Куб повернут вокруг прямой, соединяющей центры противоположных граней, на угол 45о. Какая фигура является общей частью исходного куба и повернутого?

Упражнение 26Куб повернут вокруг диагонали на угол 60о. Какая фигура является общей частью исходного куба и повернутого?

Упражнение 27Куб повернут вокруг прямой, соединяющей середины противоположных ребер, на угол 90о. Какая фигура является общей частью исходного куба и повернутого?Ответ: Две правильные 4-е пирамиды, поставленные на основания правильной 4-ой призмы.

Упражнение 28Октаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол 45о. Какая фигура является общей частью исходного октаэдра и повернутого?

Упражнение 29Октаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на угол 60о. Какая фигура является общей частью исходного октаэдра и повернутого?