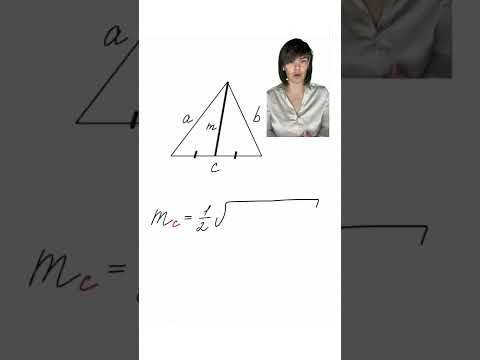Как построить треугольник из медиан (4 видео)

Построение треугольника по трем медианам ma, mb, mc

Построения треугольников осуществляется по основным и так вспомогательным элементам. К последним относят, радиусы вписанной и описанной окружностей, а также биссектрисы, медианы и высоты. В основном такие задачи решаются применением метода вспомогательного треугольника, при котором его построение сводится к какой либо уже известной задаче по основным элементам.

Построим вспомогательный треугольник НВР по трем сторонам равным медианам ma, mb, mc, заданным по условию (см. рис.). Отложим на стороне НВ отрезок НО = 1/3 НВ. Затем через точку О проведем прямую параллельно ВР. Она пересечет сторону треугольника НР в точке К. От точки К отложим отрезок КС = ОК, а от точки О — отрезок ОМ, тем же раствором циркуля. Соединим точку В с точкой С. Через точки В и М, С и Н проведем прямые до их пересечения в точке А.

Проведем в построенном треугольнике АВС дополнительно две медианы МС и АЕ. Докажем, что МС = РВ, а АЕ = НР. Треугольники НВР и НОК подобны с коэффициентом подобия 3. Аналогично треугольники АОС и НКС — с коэффициентом подобия 2. Откуда ОК = КС = 1/2 ОС= 1/3 mc, а НК =1/2 АО = 1/3 ma. Следовательно, построен искомый треугольник АВС.

Предлагаемый способ отличается содержанием значительно меньшего количества шагов в построении.

19.01.2016 г. / Стрижак Василий Васильевич/ г. Речица, Гомельская обл.

Содержание

Как построить треугольник по трем медианам?
Определение и свойства медианы треугольника
Определение медианы треугольника
Свойства медианы
Свойство 1 (основное)
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Примеры задач
💡 Видео

Видео:Построение медианы в треугольникеСкачать

Как построить треугольник по трем медианам?

Построения треугольников осуществляется как по основным и так вспомогательным элементам. К последним относят, радиусы вписанной и описанной окружностей, а также биссектрисы, медианы и высоты. В основном такие задачи решаются применением метода вспомогательного треугольника, при котором его построение сводится к какой либо уже известной задаче по основным элементам. В предлагаемом решении вспомогательный треугольник, стороны которого равны медианам ma, mb, mc, является основой построения искомого треугольника.

Построим вспомогательный треугольник НВР по трем сторонам равным медианам ma, mb, mc, заданным по условию (см. рис.). Отложим на стороне НВ отрезок, НО = 1/3 НВ. Затем через точку О проведем прямую параллельно ВР. Она пересечет сторону треугольника НР в точке К. От точки К отложим отрезок КС = ОК, а от точки О — отрезок ОМ, тем же раствором циркуля. Соединим точку В с точкой С. Через точки В и М, С и Н проведем прямые до их пересечения в точке А.

Проведем в построенном треугольнике АВС дополнительно две медианы МС и АЕ. Докажем, что МС = РВ, а АЕ = НР. Треугольники НВР и НОК подобны с коэффициентом подобия 3. Аналогично треугольники АОС и НКС — с коэффициентом подобия 2. = КС = ½ ОС= 1/3 mc, а НК =½ АО = 1/3 ma. Следовательно, построен искомый треугольник АВС.

Предлагаемый способ отличается содержанием значительно меньшего количества шагов в построении.

Видео:Построение высоты в треугольникеСкачать

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Видео:Как построить треугольник по двум сторонам и медиане, проведенной к третьей сторонеСкачать

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5: