В прямоугольном параллелепипеде ABCDA1B1C1D1 через диагональ BD1 проведена плоскость α, параллельная прямой AC.
б) Найдите угол между проведённой плоскостью и плоскостью основания параллелепипеда, если AB = 6, BC = 8, CC1 = 10.
б) Пусть B1M — перпендикуляр, опущенный из вершины B1 на прямую l. Тогда B1M — ортогональная проекция наклонной BM на плоскость A1B1C1D1. По теореме о трёх перпендикулярах прямые BM и l перпендикулярны, поэтому угол BMB1 — линейный угол двугранного угла, образованного секущей плоскостью α и плоскостью A1B1C1D1.
Отрезок B1M вдвое больше высоты B1H прямоугольного треугольника A1B1C1, проведённой из вершины прямого угла, поэтому
Из прямоугольного треугольника BMB1 находим, что
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать 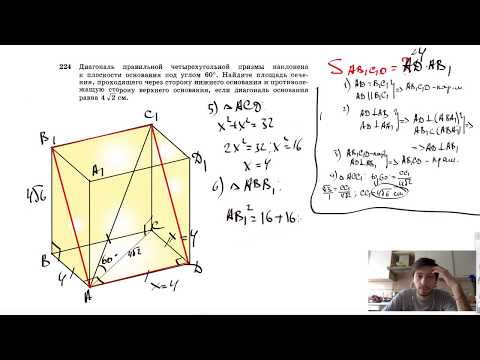 Через диагональ bd1 правильной четырехугольной призмы проведена плоскость a параллельная прямой acЗадание 8. В правильной четырёхугольной призме ABCDA1B1C1D1 ребро АА1 равно 10, а диагональ BD1 равна 26. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и С. У правильной четырехугольной призмы в основании лежит квадрат и диагонали BD1=AC1. Рассмотрим прямоугольный треугольник AA1C1, в котором известен катет AA1=10 и гипотенуза AC1=26. По теореме Пифагора найдем катет A1C1:
Соответственно, площадь сечения равна
Видео:№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать 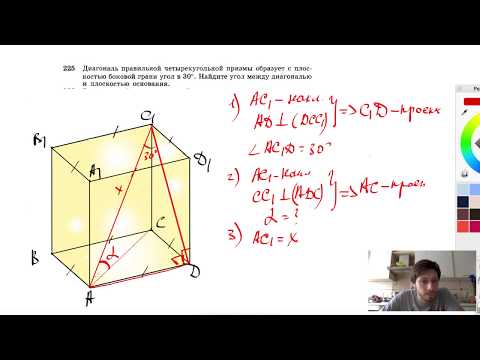 Через диагональ bd1 правильной четырехугольной призмы проведена плоскость a параллельная прямой acБАЗА ЗАДАНИЙ Задание № 5. Стереометрия. 1. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы. 2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. 3. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза? 4. Площадь поверхности куба равна 24. Найдите его объем. 5. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба. 6. Площадь поверхности куба равна 8. Найдите его диагональ. 7. Объем куба равен 24√3. Найдите его диагональ. 8. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. 9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы. 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы. 11. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. 12. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. 13. В основании прямой призмы лежит ромб с диагоналями, равными 9 и 12. Площадь ее поверхности равна 468. Найдите боковое ребро этой призмы. 14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности. 15. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. 16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ. 17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. 18. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. 19. Диагональ прямоугольного параллелепипеда равна √8 и образует углы 30°,30° и 45° с плоскостями граней параллелепипеда. Найдите объем параллелепипеда. 20. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что BB 1 =32, AB=12, AD=9. Найдите площадь сечения проходящее через вершины A, A 1 , C. 22. Дана правильная четырёхугольная призма ABCDA 1 B 1 C 1 D 1 , площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, B 1 . 23. Найдите объём многогранника, вершинами которого являются точки C, A1 , B1 , C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 4, а боковое ребро равно 9. 24. Найдите объём многогранника, вершинами которого являются точки A, C, A 1 , B1, C 1 правильной треугольной призмы ABCA 1 B 1 C 1 . Площадь основания призмы равна 7, а боковое ребро равно 9. 25. В правильной треугольной призме ABCA 1 B 1 C 1 все ребра равны 3. Найдите угол между прямыми AA1и BC1. Ответ дайте в градусах. 26. В правильной треугольной призме ABCA 1 B 1 C 1 известно, что AB=√3AA 1 . Найдите угол между прямыми AB1 и CC1. Ответ дайте в градусах. 27. Объём куба равен 16. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины. 28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. 29. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 4,5. Найдите объем треугольной пирамиды AD 1 CB 1 . 30. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 1,5. Найдите объем треугольной пирамиды ABCB 1 . 31. Найдите объем параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объем треугольной пирамиды ABDA 1 равен 3. 32. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол 60° и равно 2. Найдите объем параллелепипеда. 33. Найдите объём многогранника ACDFA 1 C 1 D 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 9, а боковое ребро равно 11. 34. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E 1 D 1 . 35. Найдите объём многогранника DA 1 B 1 C 1 D 1 E 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 2. 36. Найдите объём многогранника CDEC 1 D 1 E 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 6, а боковое ребро равно 14. 37. Найдите объём многогранника A 1 B 1 F 1 A правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 15. 38. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём. 39. В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды. 40. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4. 41. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды. 42. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды. 📽️ Видео№226. В правильной четырехугольной призме через диагональ основания проведено сечениеСкачать 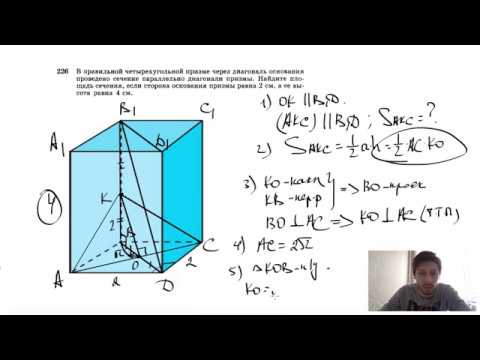 Задача о вычислении диагонали четырёхугольной призмыСкачать  В правильной четырёхугольной призме ABCDA1B1C1D1 ребро АА1 равно 15, а диагональ BD1 равна 17.Скачать  Стереометрия, номер 28.1Скачать  СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  №195. Найдите измерения прямоугольного параллелепипеда AD1, если АС1 = 12 см и диагональ BD1Скачать  10 класс, 30 урок, ПризмаСкачать  №69. Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SBСкачать  Стереометрия 39 | mathus.ru | угол между плоскостями в прямой четырёхугольной призмеСкачать  Призма.Все виды задач на ЕГЭ.52 задачи.№8 ПрофильСкачать  Самый сложный пример 5 задание проф. ЕГЭ (часть III)Скачать  ✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2019. Задание 13. Математика | Борис ТрушинСкачать  296. Высота правильной треугольной призмы равна h. Плоскость α, проведенная через среднюю линиюСкачать  Как строить сечения параллелепипедаСкачать  ЕГЭ-2020 по математике: площадь боковой поверхности треугольной призмыСкачать  ✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать  №221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать  |

 .
. .
.
















