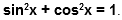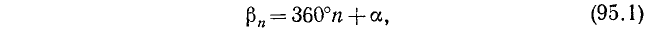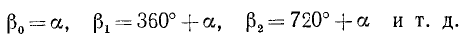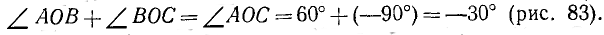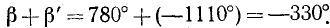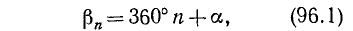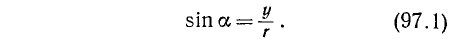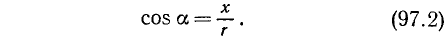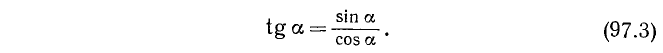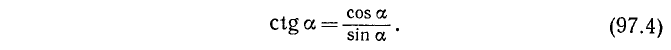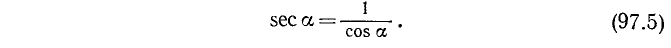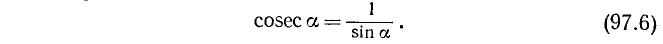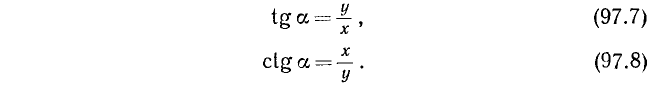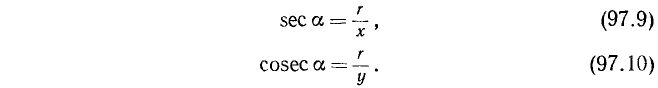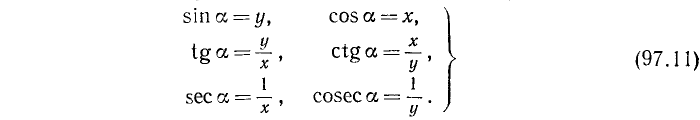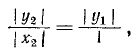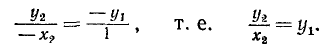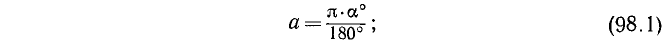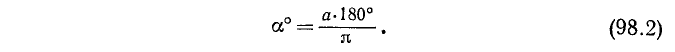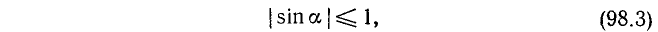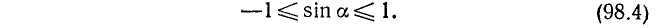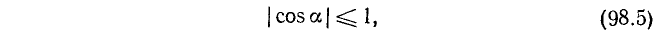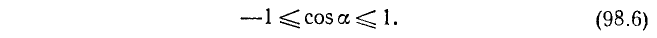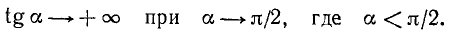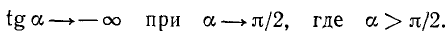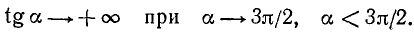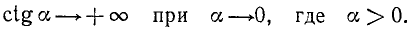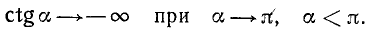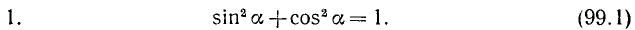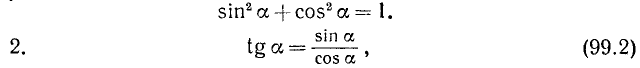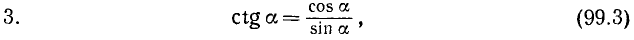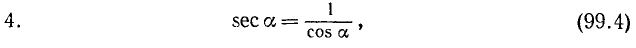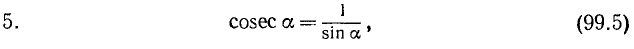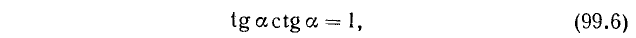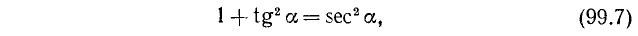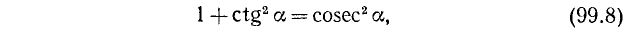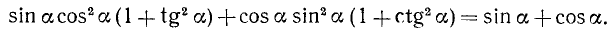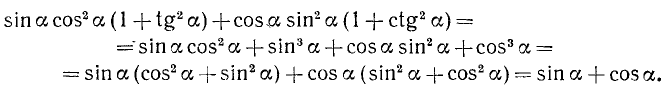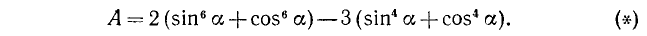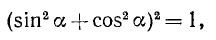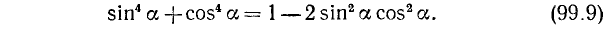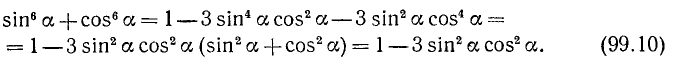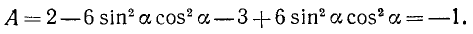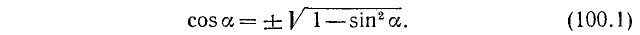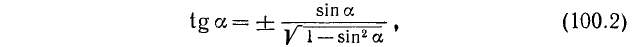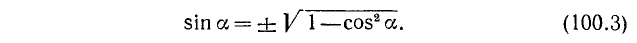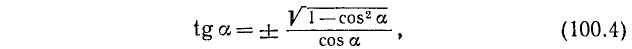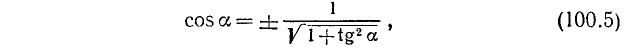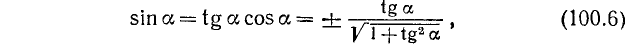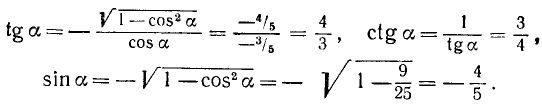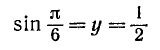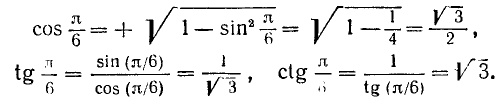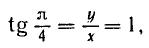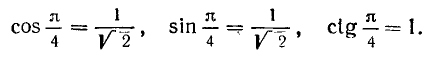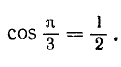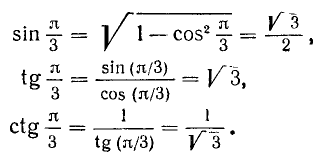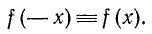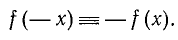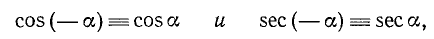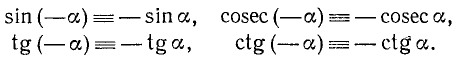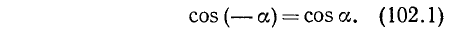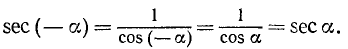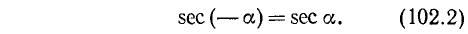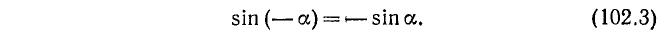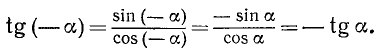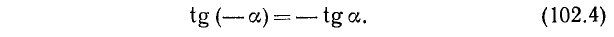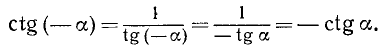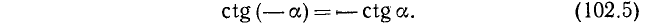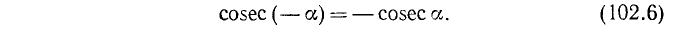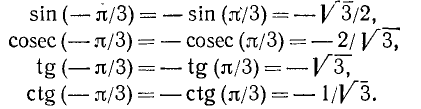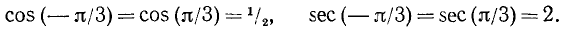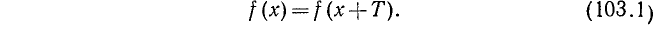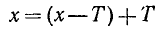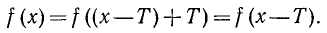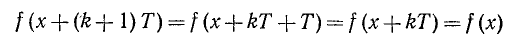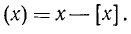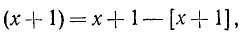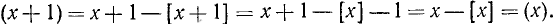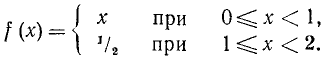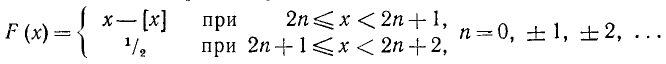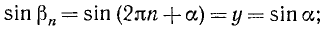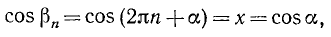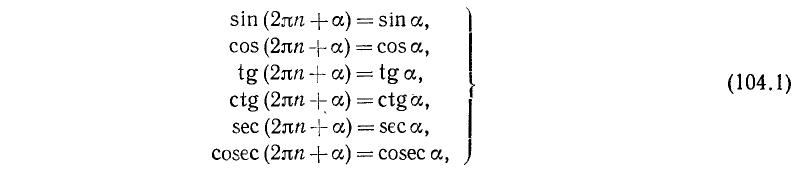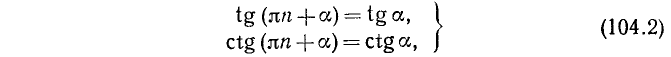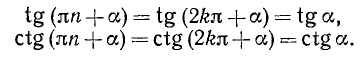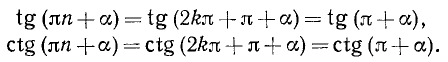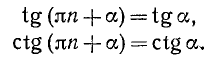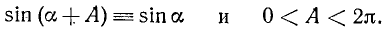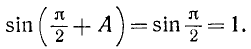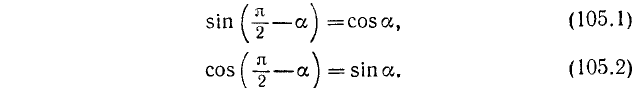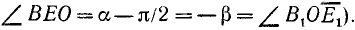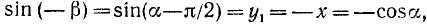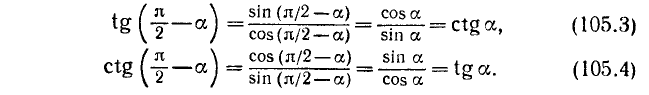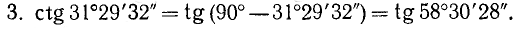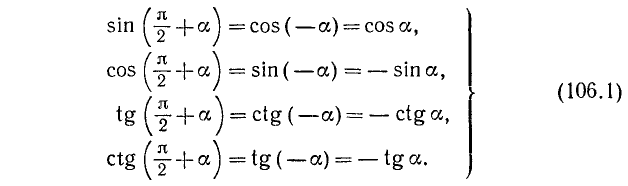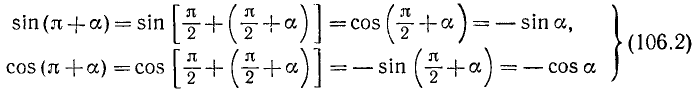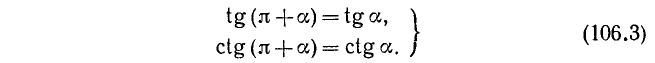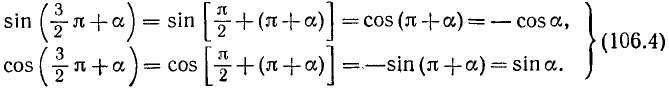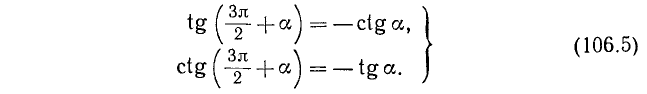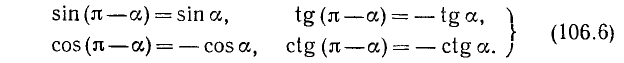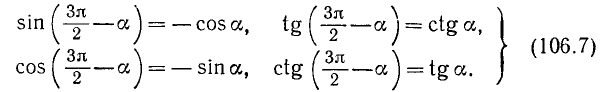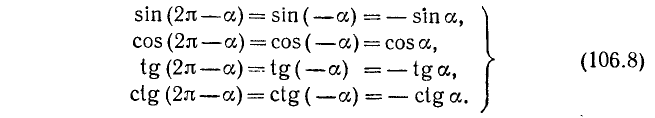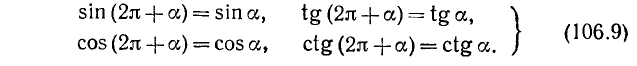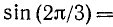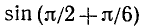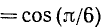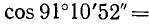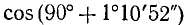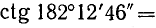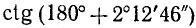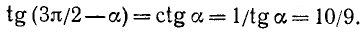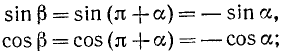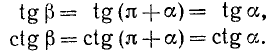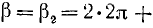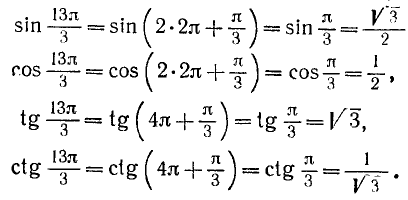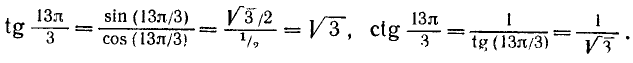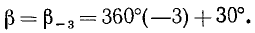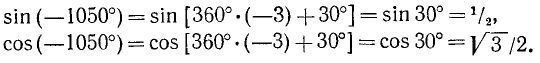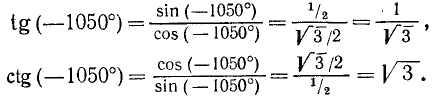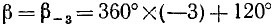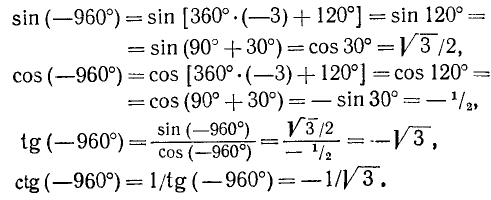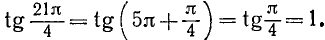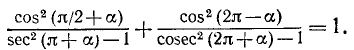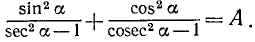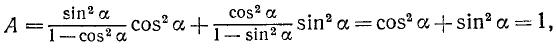О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Единичная окружность в тригонометрии
- Алгебра
- Числовая и единичная окружность
- Откладывание углов на единичной окружности
- Тригонометрические функции угла (дуги) в математике с примерами решения и образцами выполнения
- Векторы. Обобщение понятий угла и дуги. Проекция вектора
- Положительные углы и дуги, меньшие 360°
- Углы и дуги, большие 360°
- Отрицательные углы. Сложение и вычитание углов
- Тригонометрические функции произвольного угла
- Изменение основных тригонометрических функций при изменении угла от 0 до 2 пи
- Соотношения между тригонометрическими функциями одного и того же угла
- Вычисление значений тригонометрических функций по значению одной из них
- Значения тригонометрических функций некоторых углов
- Четность, нечетность и периодичность тригонометрических функций
- Понятие периодической функции
- Периодичность тригонометрических функций
- Зависимость между тригонометрическими функциями дополнительных углов
- Формулы приведения
- 🔥 Видео
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Алгебра
План урока:
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Видео:Радианная мера угла. 9 класс.Скачать

Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
Видео:Знаки тригонометрических функций. 9 класс.Скачать
Тригонометрические функции угла (дуги) в математике с примерами решения и образцами выполнения
Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Векторы. Обобщение понятий угла и дуги. Проекция вектора
Вектором называется направленный отрезок в плоскости (в пространстве). При изучении тригонометрических функций мы будем рассматривать векторы в плоскости. С каждым вектором связывают понятия направления и длины (абсолютной величины, модуля).
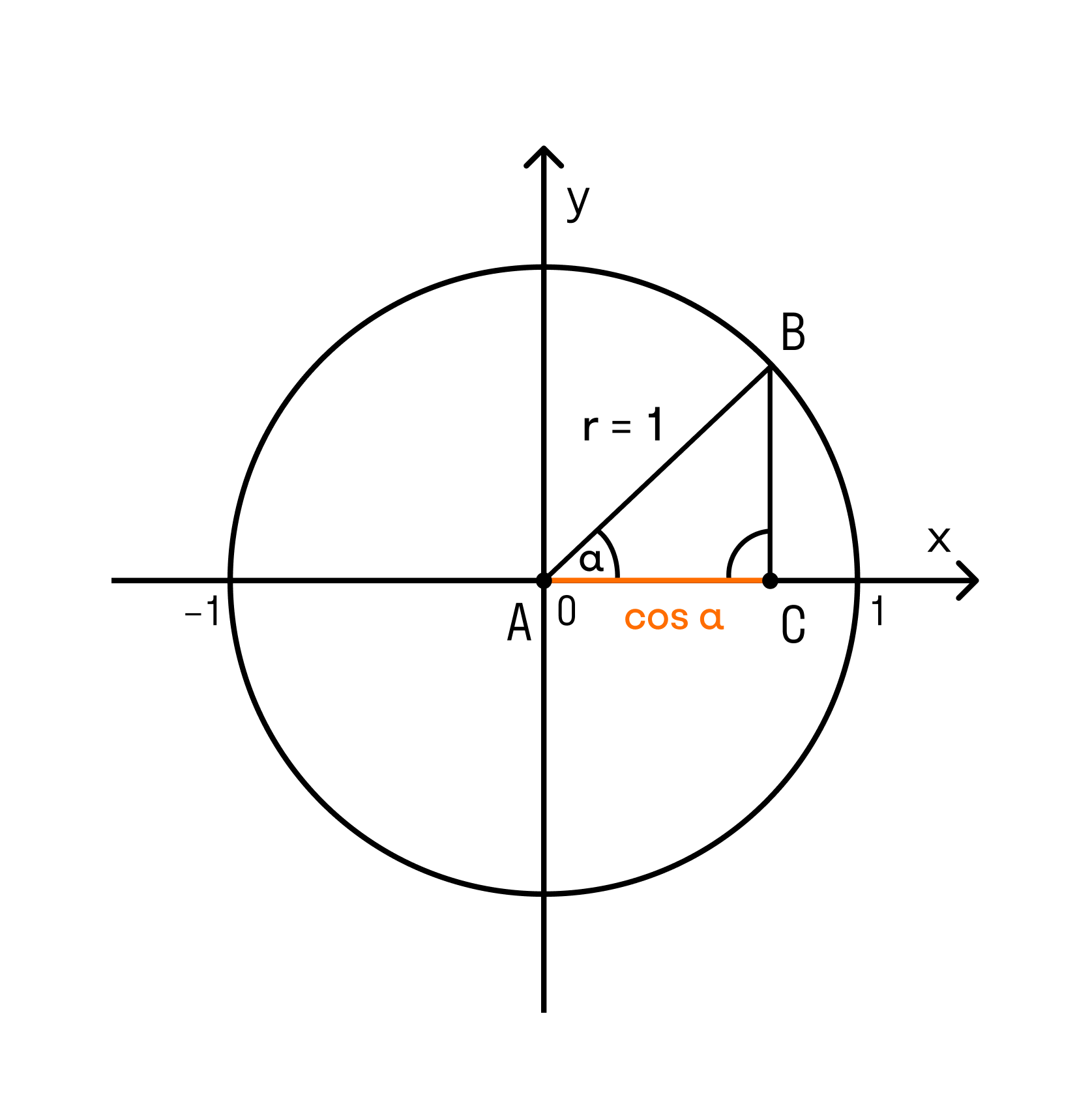
Для вектора (рис. 73) применяются следующие обозначения: 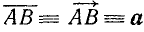
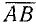
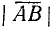
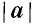
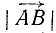
Для общности рассматривается и случай нулевого отрезка АА, начало которого совпадает с его концом. Такой отрезок называется нулевым вектором и обозначается через 0. Нулевой вектор имеет длину, равную нулю; ему не приписывается никакого направления.
Следует заметить, что всегда 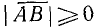
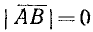
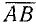
Для векторов не имеют смысла понятия «больше» или «меньше». Можно только говорить, что длина вектора 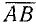
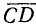
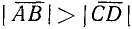
Два Еектора а и b называются равными, если они:
1) параллельны одной и той же прямой,
2) одинаково направлены,
3) имеют равные длины, т. е. |a| = |b| (рис. 74).
Совокупность векторов с указанным выше определением равенства обычно называют системой свободных векторов. Термин «свободный вектор» связан с тем, что теперь один и тот же вектор может быть изображен направленным отрезком с началом в любой точке: его можно свободно переносить из точки в точку.
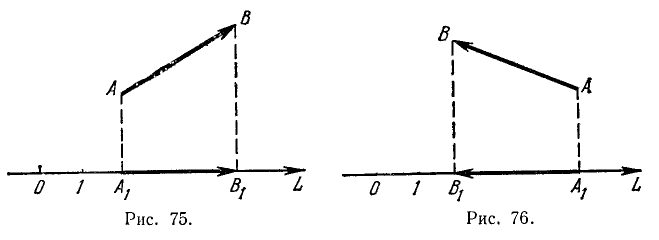
Каждому вектору 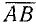
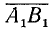
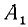
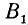
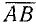
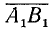
взятая со знаком плюс, если направление вектора 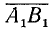
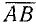
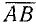
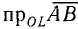
случаи: a) 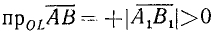
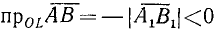
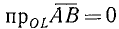
Рассмотрим теперь совокупность векторов, исходящих из одной точки (начала). Такая совокупность векторов называется центрированной. Примем эту общую точку за начало О декартовой прямоугольной системы координат Оху (см. п. 8).
Определение:
Вектор 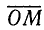
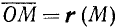
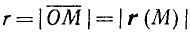
Положительные углы и дуги, меньшие 360°
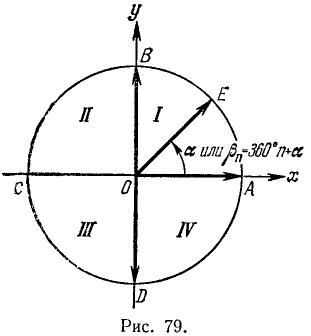
На координатной плоскости Оху рассмотрим окружность радиуса R с центром в начале координат (рис. 79).
Будем считать, что угол 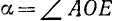
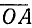
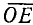
При вращении (в направлении против движения часовой стрелки) подвижный радиус-вектор описывает углы от 0° до З60° (определение градуса см. в п. 165). Осями координат круг на рис. 79 делится на четыре четверти: первая четверть АОВ, вторая BОС, третья COD и четвертая DOА. Если сторона ОЕ угла АОЕ расположена в первой, второй, третьей или четвертой четверти, то угол АОЕ будем называть соответственно углом первой, второй, третьей или четвертой четверти. В первой четверти угол 
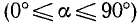
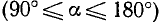
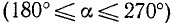
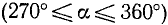
Если подвижный радиус-вектор описал угол АОЕ, равный 
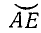

Углы и дуги, большие 360°
Мы ограничивались углами от 0° до 360°. Между тем в различных задачах приходится иметь дело с вращениями, при которых совершается больше полного оборота, например с вращением маховика, с полетом спутника вокруг Земли и т. д. Эти задачи приводят к необходимости обобщения понятия угла (дуги), к необходимости введения углов (дуг), больших 360°. Рассмотрим угол 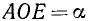
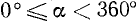
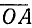
где 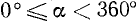
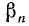



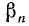
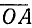
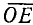
Если подвижный радиус-вектор описал угол 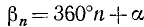
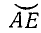
Отрицательные углы. Сложение и вычитание углов
Назовем вращение подвижного радиуса-вектора в направлении против движения часовой стрелки положительным, а в противоположном направлении (в направлении по движению часовой стрелки) — отрицательным. Угол, описанный при отрицательном вращении подвижного радиуса-вектора, назовем отрицательным углом.
Правило. Угол измеряется положительным числом, если он положительный, и отрицательным числом, если он отрицательный.
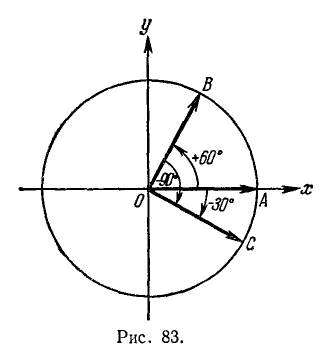
Пример:
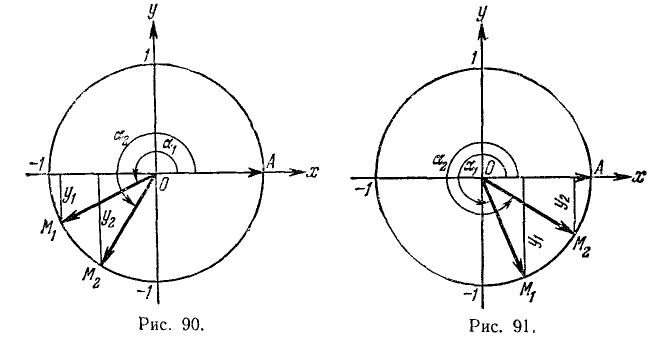
На рис. 80 изображены два угла с общей начальной стороной 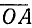
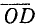
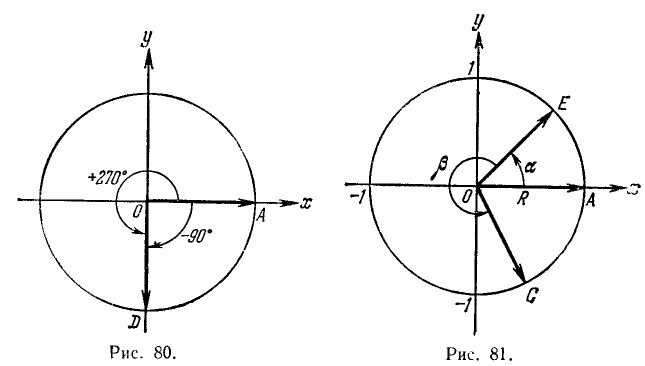
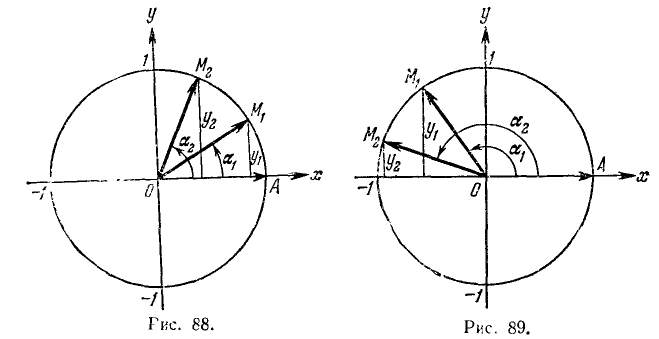
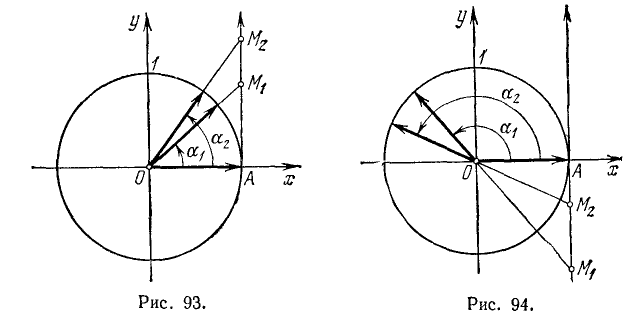
Сумма двух углов. Па координатной плоскости Оху рассмотрим окружность единичного радиуса с центром в начале координат (рис. 81). Пусть произвольный угол 
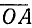
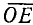
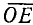
(на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения 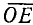
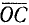

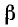
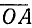
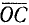
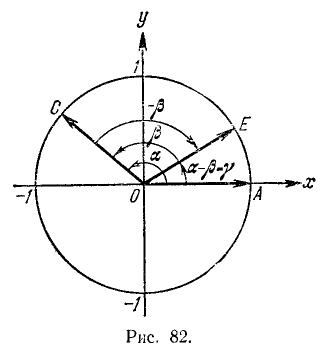
Разность двух углов. Под разностью двух углов 
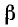

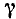
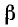

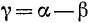
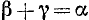

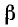

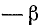
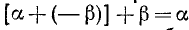
Пример:
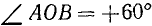
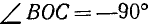
Пример:
Угол 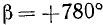
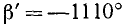
В формуле (95.1) предполагалось, что n — любое целое неотрицательное число. Если же предположить, что n —любое целое число (положительное, отрицательное или нуль), то при помощи формулы
где 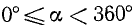
Пример:
Угол, равный —1370°, можно записать так:
—1370° = 360° (—4)+ 70°.
Здесь n = —4, 
Заметим, что все углы 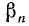
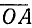
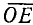

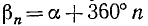
Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Тригонометрические функции произвольного угла
Определение основных тригонометрических функций: Было дано общее определение функциональной зависимости (общее определение функции) и изучались некоторые элементарные функции. Теперь мы введем основные тригонометрические функции.
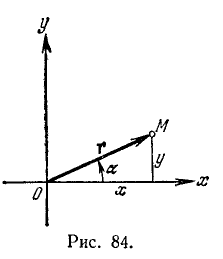
Пусть радиус-вектор 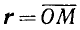


1 . Синусом угла 
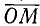
2. Косинусом угла 
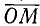
Ниже (замечание 1) мы покажем, что sin а и cos а, определенные равенствами (97.1) и (97.2), действительно зависят лишь от угла а (но не от радиуса окружности r).
3. Тангенсом угла а (обозначение: tg a) называется отношение синуса угла а к косинусу этого угла:
4. Котангенсом угла а (обозначение: ctg a) называется отношение косинуса угла а к синусу этого угла:
5. Секансом угла a (обозначение: sec а) называется величина, обратная cos а:
6. Косекансом угла а (обозначение: cosec a) называется величина, обратная sin а:
Замечание:
Тригонометрические функции (97.1) — (97.6) действительно являются функциями только угла а, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор r образует с осью абсцисс данный угол а, то отношения х/r и у/r не зависят от длины радиуса-вектора; читатель легко в этом убедится.
Замечание:
Из определения tg a и ctg a следует, что
Соотношения (97.7) и (97.8) можно было бы принять в качестве определений для tg a и ctg a.
Замечание:
Соотношения (97.9) и (97.10) можно было качестве определений для sec а и cosec a.
Замечание 4. Во всех определениях (97.1) — (97.6) мы предполагаем, что соответствующие отношения существуют (имеют смысл). Например, tg a имеет смысл, если 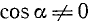
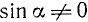
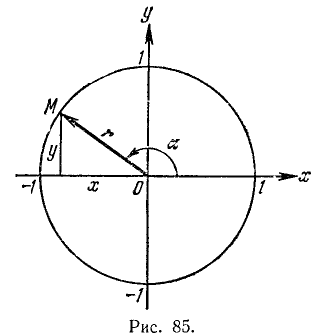
В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис. 85):
Формулы для tg a и ctg a остались прежними (см. (97,7) и (97.8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (97.1), (97.2), (97.9) и (97.10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора.
Конец этого единичного радиуса-вектора при изменении угла а от 0° до 360° опишет окружность, называемую единичной окружностью (рис. 85). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов.
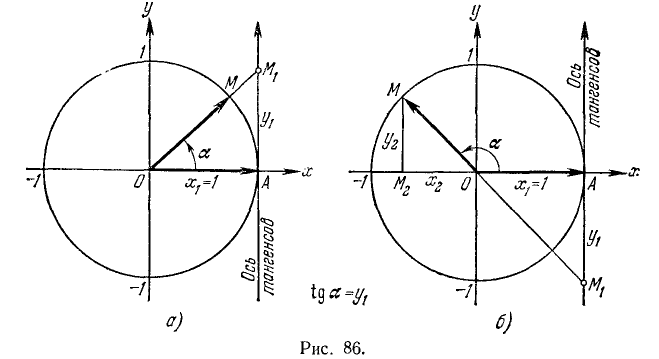
Осью тангенсов называется перпендикуляр, восставленный в точке А к неподвижному радиусу-вектору 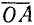
Рассмотрим угол 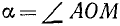
а) Если точка М единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку 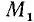
б) Если точка М единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку 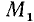
Заметим, что тангенс угла а численно равен ординате 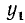
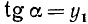
1) 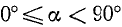
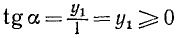
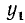
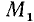
2) 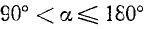
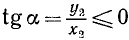
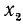
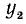
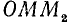
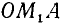
Следовательно, 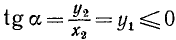
Заметим еще следующее:
а) если точка М лежит на оси ординат (например, а = 270°), то соответствующей ей точки оси тангенсов не существует, но при этом и tg a также не существует;
б) в рассмотренных случаях 1) — 4) мы брали угол а в пределах от 0° до 360°, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол а любым.
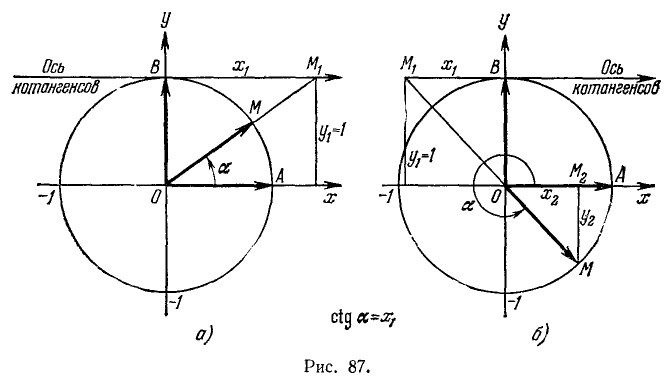
Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора 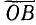
Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис. 87). Введем понятие соответствующей точки оси котангенсов.
а) Если точка М единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку 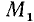
б) Если точка М единичной окружности лежит под осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку 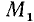
Аналогично предыдущему можно получить, что котангенс угла а равен абсциссе х, соответствующей точки оси котангенсов, т.е. 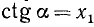
Изменение основных тригонометрических функций при изменении угла от 0 до 2 пи
Изменение основных тригонометрических функций при изменении угла от 0 до 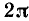
В дальнейшем мы будем использовать не только градусную, но и радианную меру углов (см. п. 166); радианное измерение углов станет особенно важным при переходе к тригонометрическим функциям числового аргумента (п. 107). В связи с этим напомним некоторые факты из геометрии, относящиеся к градусной и радианной системам измерения углов и дуг:
1) при измерении углов и дуг в радианной системе наименование единицы измерения — радиана обычно опускают и говорят, например, «угол равен 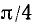
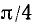
2) при переходе от градусной меры (а градусов) к радианной мере (а радиан) пользуются формулой
3) при переходе от радианной меры (а радиан) к градусной мере (а градусов) пользуются формулой
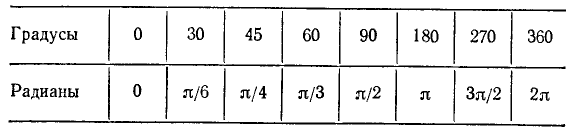
Полезно запомнить соответствующие значения в градусной и радианной мере некоторых наиболее часто встречающихся углов, приведенные в следующей таблице.
Рассмотрим теперь, как изменяется (по абсолютной величине и знаку) каждая из основных тригонометрических функций при изменении угла а от 0 до 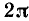
I. sin а. Согласно первой формуле (97.11) sin a = у, где у — ордината конца подвижного единичного радиуса-вектора (см. рис. 85).
1) 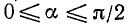
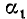
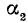
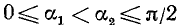
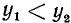
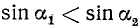
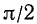
2) 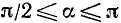
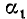
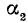
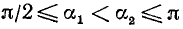
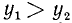
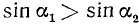
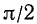
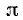
3) 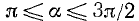
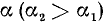
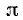
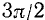
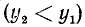
4) 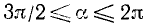
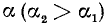
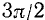
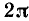

Вывод. При любом угле а абсолютная величина sin а не превосходит 1, что записывается так:
или в равносильной форме:
II. cos а. По второй формуле (97.11) cos a = x, где х — абсцисса конца подвижного единичного радиуса-вектора (рис. 85).
1) 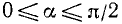
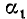
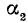
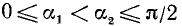
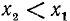
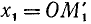
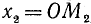
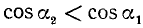
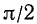
2) 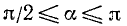
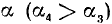
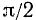
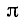
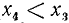
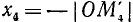
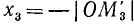
3) 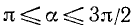
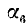
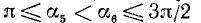
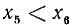
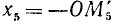
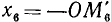
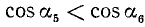
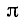
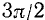
4) 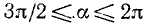
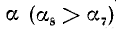
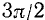
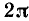
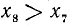
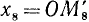
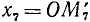
Вывод. При любом угле а абсолютная величина cos а не превосходит 1, что записывается так:
или в равносильной форме:
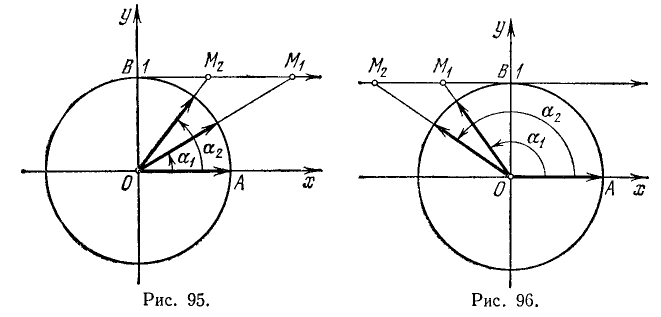
III. tg a. Тангенс угла а численно равен ординате соответствующей точки оси тангенсов (см. п. 97).
1) 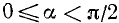
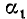
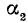
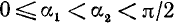
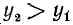
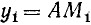
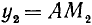
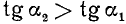
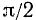
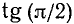
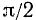
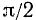
Сходное положение встречалось при изучении функции у = 1/х; если х приближается к нулю, оставаясь больше нуля, то у = 1/х стремится к плюс бесконечности.
Это же условно записывают так:
2) 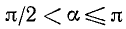
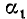
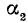
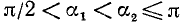
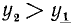
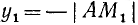
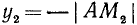

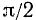
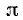
Если а стремится к 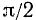
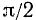
3) 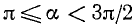
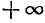
Если а стремится к 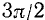
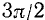
4) 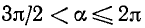
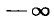
Если а стремится к 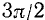
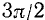
IV. ctg a. Котангенс угла а численно равен абсциссе соответствующей точки оси котангенсов (см. п. 97).
1) 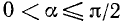
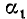
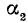
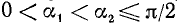

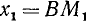
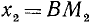
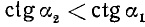
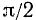
2) 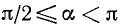
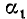
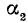
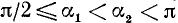
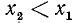
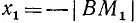
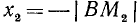
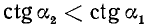
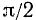
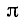
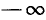
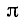
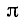
Разбор поведения ctg a в остальных четвертях предоставляется читателю. Приведем только окончательные результаты:
3) 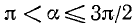
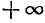
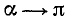
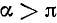
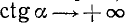
4) 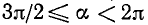
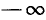
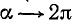
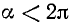
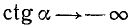
Видео:Как искать точки на тригонометрической окружности.Скачать

Соотношения между тригонометрическими функциями одного и того же угла
Основные тригонометрические тождества: Между основными тригонометрическими функциями произвольного угла а имеются следующие тождественные соотношения:
Доказательство. Принимая |r| = r = 1, получим (для произвольного угла a) sin а = у, cos a = x, где х и y — проекции единичного радиуса-вектора на оси координат (см. рис. 85). По теореме Пифагора (см. п. 216) 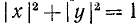
где 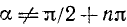
где 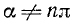
Тождества (99.2) и (99.3) служат соответственно определениями функций tg a и ctg a (см. формулы (97.3) и (97.4)).
где 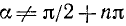
где 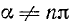
Тождества (99.4) и (99.5) служат соответственно определениями функций sec а и cosec а (см. формулы (97.5) и (97.6)).
Тождества (99.1)—(99.5) назовем основными. При помощи этих основных тождеств выведем так называемые дополнительные тождества.
6. Перемножив почленно тождества (99.2) и (99.3), получим
где 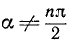
7. Разделив тождество (99.1) почленно на 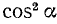
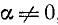
где 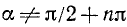
8. Разделив тождество (99.1) почленно на 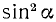
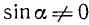
где 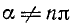
При помощи тождеств (99.1)—(99.8) можно производить преобразования различных выражений, содержащих тригонометрические функции, и получать новые тождества. Пример 1. Доказать тождество
Решение:
Заменив в левой части tg a и ctg a их выражениями по формулам (99.2) и (99.3), получим
После выполнения тождественных преобразований левая часть равенства совпала с правой. Исходное тождество этим доказано.
Это же тождество можно доказать и по-другому, воспользовавшись формулами (99.7) и (99.8), а затем формулами (99.4) и (99.5). Рекомендуем это сделать читателю.
Пример:
Решение:
Используя тождество (99.1), получаем
Подставив (99.9) и (99.10) в (*), будем иметь
Вычисление значений тригонометрических функций по значению одной из них
При помощи формул (99.1)—(99.8) можно выразить (с точностью до знака) через любую из шести тригонометрических функций угла а остальные пять функций. Мы ограничимся только функциями sin a, cos а и tg a.
1 . Выражение через sin а. Из тождества (99.1) находим
Подставив найденное значение cos а в тождество (99.2), получим
где 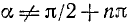
2. Выражение через cos а. Из тождества (99.1) находим
Подставив найденное значение sin а в тождество (99.2), получим
где 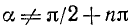
3. Выражение через tg a. Из тождества (99.7) находим 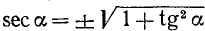
где 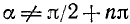
где 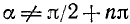
При извлечении квадратного корня знак следует выбирать в зависимости от того, в какой четверти находится угол а.
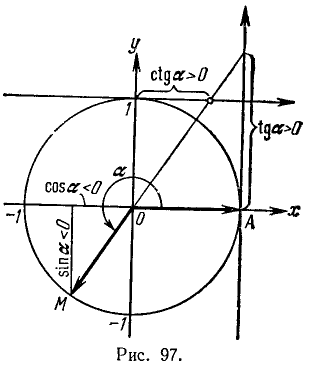
Пример:
Известно, что cos a = —3/5 и 180° 0, ctg a > 0, sin a
В дальнейшем мы будем использовать следующий факт:
Для того чтобы два действительных числа х и у можно было принять за cos а и sin а одного и того же угла а, необходимо и достаточно, чтобы сумма их квадратов была равна единице: 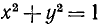
Доказательство:
Необходимость. Если х = cos а и у = sin а, то по тождеству (99.1) 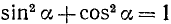
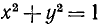
Достаточность. Рассмотрим радиус-вектор 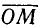
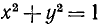
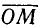
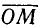
Пример:
Могут ли sin а и cos а одного и того же угла a быть равными соответственно: а) 12/13 и —5/13; б) 1/3 и —2/3?
Решение:
а) Числа 12/13 и —5/13 обладают тем свойством, что 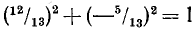
б) Для чисел 1/3 и —2/3 имеем 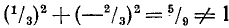
Значения тригонометрических функций некоторых углов
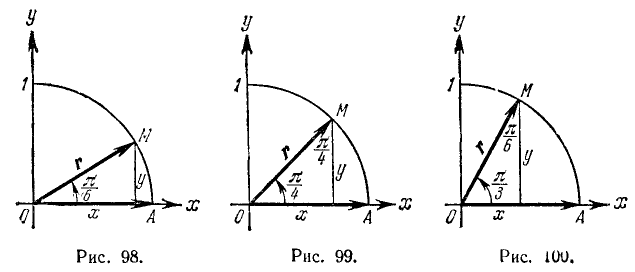
Воспользовавшись сведениями из геометрии, найдем значения тригонометрических функций углов 30°, 45° и 60° (или соответственно в радианной мере углов 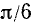
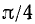
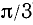
1) 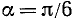
(поскольку r = 1). Воспользовавшись теперь формулами (100.1), (99.2) и (99.6), легко вычислим:
2) 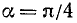
ибо у = х. Воспользовавшись теперь формулами (100.5), (100.6) и (99.6), легко найдем:
3) 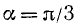
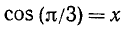
Далее воспользуемся формулами (100.3), (99.2) и (99.6):
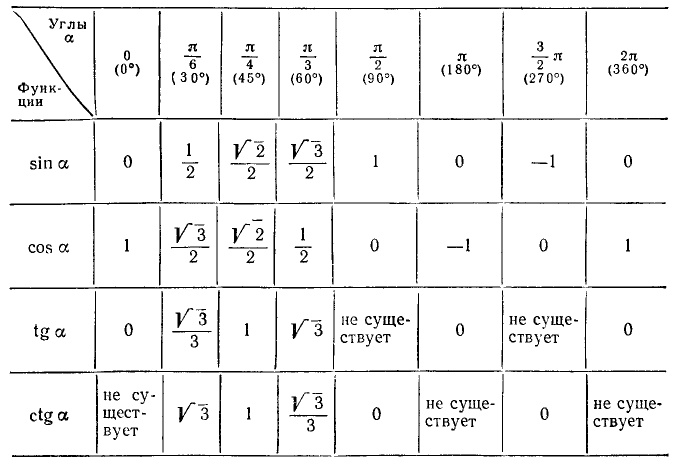
Присоединяя к полученным результатам результаты п. 98, составим следующую таблицу значений тригонометрических функций некоторых часто встречающихся углов.
О поведении tga a окрестности 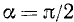
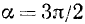
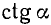
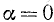
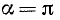
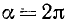
Четность, нечетность и периодичность тригонометрических функций
Четность и нечетность: Напомним (см. п. 33), что функция y = f(x) называется четной, если для всех допустимых значений аргумента х имеет место тождество
Функция y = f(x) называется нечетной, если для всех допустимых значений аргумента x имеет место тождество
Для тригонометрических функций справедлива следующая
Теорема:
Функции cos а и sec а являются четными, т.е.
а функции sin а, tg a, ctg a и cosec а являются нечетными, т. е.
Доказательство:
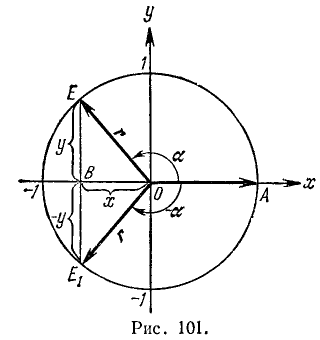
Рассмотрим два угла, образованных единичным радиусом-вектором r: 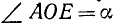
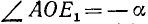
Согласно второй формуле (97.11) имеем cos a = x и cos (—а) = х, следовательно,
cos(—a) = cosa. (102.1)
Так как равенство (102.1) справедливо для любого угла а, то мы доказали, что cos (— a) = cos a.
Четность sec a (см. формулу (99.4)) доказывается так:
Заметим, далее, что ординаты точек 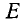
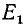
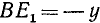
Используя формулу (99.2), а также тождества (102.1) и (102.3), получим
Для доказательства нечетности ctg a воспользуемся тождествами (99.6) и (102.4):
Рекомендуем читателю доказать, что справедливо и тождество
Пример:
Найти значения тригонометрических функций угла 
Решение:
Используя нечетность функций sin a, cosec а, tg a и ctg a, получим
Используя четность функций cos а и sec а, получим
Понятие периодической функции
Тригонометрические функции обладают свойством периодичности, которое определяется в общей форме следующим образом.
Определение. Функция f (х) называется периодической с периодом 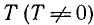
Число Т называется в этом случае периодом функции f(x). Докажем следующее предложение:
Если Т — период функции f(x), mo и любое из чисел nТ, п = —1, ±2, … , также является периодом f(x).
Доказательство:
Прозедем сначала доказательство для —Т. Для этого рассмотрим пару значений аргумента х и х+(—Т)=х—Т. Из записи
видно (в силу определения периодичности), что если функция определена в одной из точек х—Т, х, то она определена и во второй точке. Далее устанавливаем равенство f/(х—T) = f(x):
Доказательство того, что nТ при натуральном n является периодом функции f(x), проведем по индукции (случай отрицательного n сводится к этому заменой Т на —Т). Итак, требуется установить, что если f(х) определена в одной из точек x, х + nТ,
то она определена и во второй точке, причем f (x) = f (х + nТ). Допустим, что утверждение теоремы уже доказано для некоторого n = k (оно, например, очевидно при n = 1). Докажем, что оно останется верным и для n = k + 1. Прежде всего, в силу того, что Т — период, замечаем, что если одно из значений аргумента x + kT и x + (k + l)T = (x + kT) + T принадлежит области определения функции, то ей принадлежит и второе значение. Так как, по предположению индукции, такое же положение справедливо и для пары точек х и x + kT, то видно, что точки х и х + (k + 1)T принадлежат (или не принадлежат) области определения f(х) одновременно. Далее устанавливаем равенство значений f(x) в точках x и x + (k + 1)T:
(последнее — по предположению индукции).
Доказано, что nТ — период функции при любом целом n. Наименьший положительный период функции (если он существует) называется основным периодом.
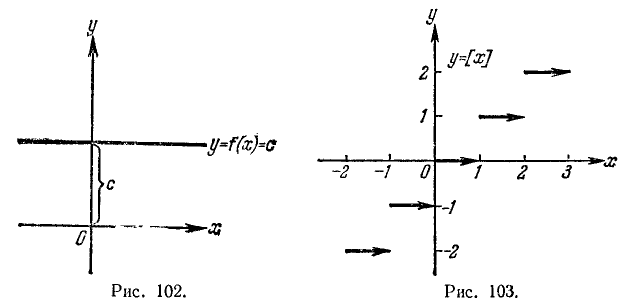
Пример:
Функция f(х) = с (с — постоянная величинa) имеет своим периодом любое число. Основного периода здесь нет. График этой функции изображен на рис. 102.
Пример:
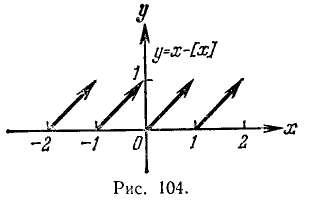
Напомним, что целой частью числа х (обозначение: [x]) называется наибольшее целое число, не превосходящее х (п. 4). Целая часть х есть функция от х; ее график показан на рис. 103.
Дробной частью числа х (обозначение: (x)) мы назвали (п. 4) разность между х и его целой частью:
Дробная часть х является периодической функцией с основным периодом T = 1. Действительно,
и так как очевидно, что [x + 1] = [х] + 1,то
График дробной части х показан на рис. 104.
Пример:
а) Рассмотрим следующую функцию f(х), определенную для х, удовлетворяющих неравенствам 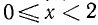
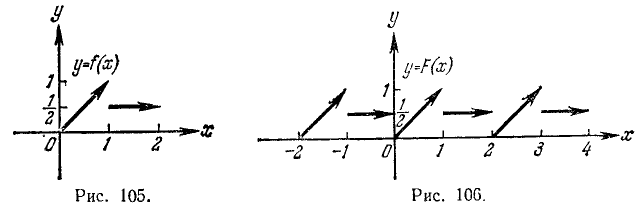
График функции изображен на рис. 105.
б) С помощью этой функции f(x), приняв за основной период число T = 2, построим периодическую функцию F (х):
График функции F (х) изображен на рис. 106.
Периодичность тригонометрических функций
Одним из важных свойств тригонометрических функций является свойство периодичности, с которым мы в общем виде познакомились в п. 103. Докажем следующую теорему о периодичности тригонометрических функций.
Теорема:
Тригонометрические функции sin a, cos а, tg a, ctg a, sec а и cosec а являются периодическими функциями, причем основной период функций sin a, cos a, sec а и cosec а равен 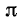
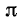
Пока мы рассматриваем тригонометрические функции угла, и период Т следует рассматривать как угол; это замечание сохраняет силу вплоть до п. 107, где вводятся тригонометрические функции числового аргумента.
Доказательство:
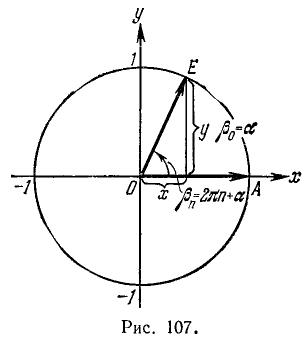
В пп. 95 и 96 мы ввели углы вида 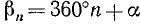
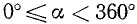
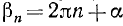
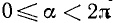
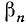
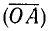
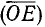
если воспользоваться второй из формул (97.11) для определения косинуса, то получим
так как соответствующие значения х и у для угла а и углов 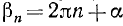
Аналогичный результат получается и для других тригонометрических функций. Мы приходим к следующим формулам:
где n = 0, ±1, ±2, …
Этим уже доказано, что 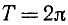
где n = 0, ±1, ±2, ...
Рассмотрим два случая.
а) n = 2k, т. е. n — четное число (k = 0, ± 1, ±2, …). В этом случае имеем
Здесь мы использовали полученные ранее формулы (104.1),
б) n = 2k + 1, т. е. n—нечетное число (k = 0, ±1, ±2, …). В этом случае имеем
Здесь мы использовали формулы (104.1).
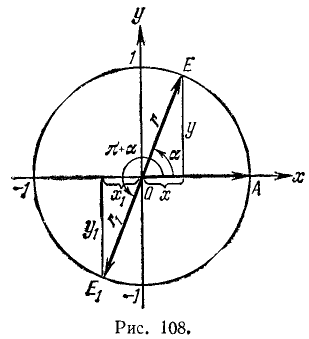
Из геометрических соображений (рис. 108) следует, что 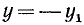
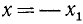
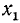
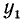
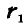
Аналогично получаем 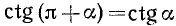
Для углов в градусной мере аналогичные формулы получим, заменив в формулах (104.1) 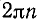
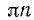
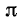
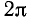
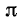
Доказательство:
Требуется показать, что 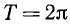
Так как в последнем равенстве а может быть любым (ведь это равенство, по предположению, выполняется тождественно), то должно выполняться, например, равенство
Но sin a = l только для аргументов а вида 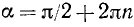
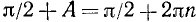
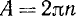
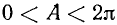
Для sin а наше утверждение доказано. Аналогично оно доказывается и для других тригонометрических функций.
Зависимость между тригонометрическими функциями дополнительных углов
Углы 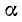
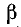
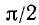
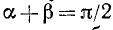
Теорема:
Сходные тригонометрические функции дополнительных углов равны между собой.
Доказательство:
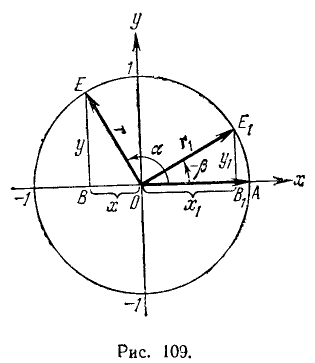
Докажем сначала, что
Предположим для определенности, что 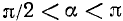
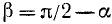
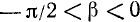
Построим теперь с помощью подвижного единичного радиуса-вектора r углы 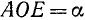
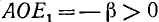
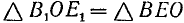
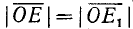
Из равенства треугольников имеем 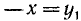
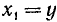
откуда 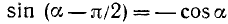
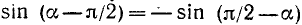
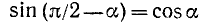
Аналогично доказывается, что 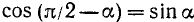
Для остальных функций можно доказательство вети так:
При выводе формул (105.3) и (105.4) мы пользовались только что доказанными формулами (105.1) и (105.2).
Замечание:
При доказательстве теоремы мы считали, что угол а задан в радианах. Соответствующие формулы для угла а, измеренного в градусной мере, легко получить из формул (105.1) —(105.4), заменив 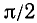
Замечание:
При доказательстве теоремы мы предположили для определенности, что угол а удовлетворяет неравенствам 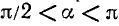
Пример:
Заменить данные тригонометрические функции тригонометрическими функциями дополнительного угла:
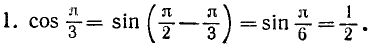
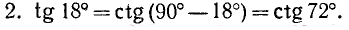
Формулы приведения
Формулами приведения называются формулы, выражающие тригонометрические функции углов 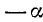
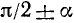
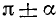
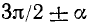
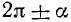
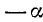
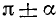
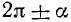
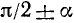
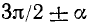
Пользуясь возможностью произвольного выбора угла а в формулах (105.1) — (105.4), получим новые важные формулы (мы ограничимся функциями sin a, cos a, tg a и ctg a).
а) Заменив в формулах (105.1)—(105.4) а на —а, получим
б) Заменив в формулах (106.1) a на 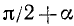
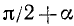
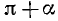
(мы снова воспользовались тем, что формулы (106.1) справедливы для произвольного угла а). Так как 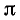
в) Аналогично получим
Рекомендуем читателю доказать, что
г) Заменив в формулах (106.2) и (106.3) а на —а, получим
д) Заменив в формулах (106.4) и (106.5) а на —а, получим
е) В силу того, что 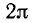
ж) Аналогично е), будем иметь
Рекомендуем читателю написать формулы, аналогичные формулам (106.1)—(106.8), для углов в градусной мере, заменив в последних 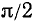
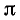
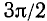
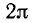
Пример:
Пользуясь формулами приведения, найти значения следующих тригонометрических функций (или выразить их через значения тригонометрических функций острых углов): а) 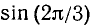
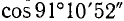
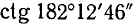
Решение:
а) 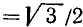
б) 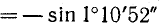
в) 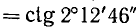
Пример:
Найти 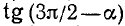
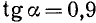
Решение:
Сформулируем теперь общее правило приведения:
1) если угол а откладывается от вертикальной оси (углы 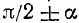
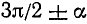
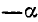
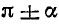
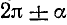
2) если приводимая функция имеет отрицательное значение, то нужно соответствующую функцию угла а взять со знаком минус, если же приводимая функция имеет неотрицательное значение, то нужно соответствующую функцию угла а взять со знаком плюс.
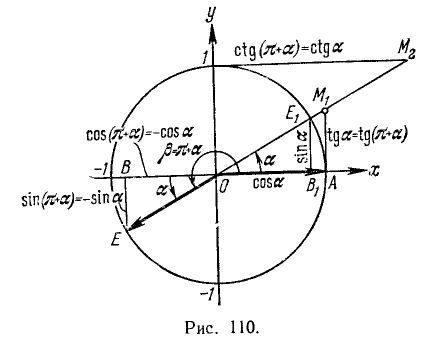
Проиллюстрируем это правило на примере угла 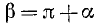
Итак, на рис. 110 угол 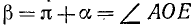
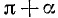
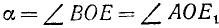
1) соответствующие названия тригонометрических функций; 2) знаки приводимых тригонометрических функций.
1) Так как угол а откладывается от горизонтальной оси (угол 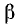
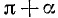
2) 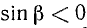
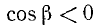
Учитывая 1) и 2), имеем
так как 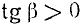
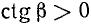
Мы пришли к формулам (106.2) и (106.3). Рекомендуем читателю проиллюстрировать на чертеже типа рис. 110 правило приведения для остальных углов (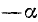
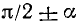

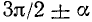
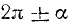
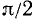
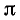
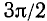
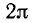
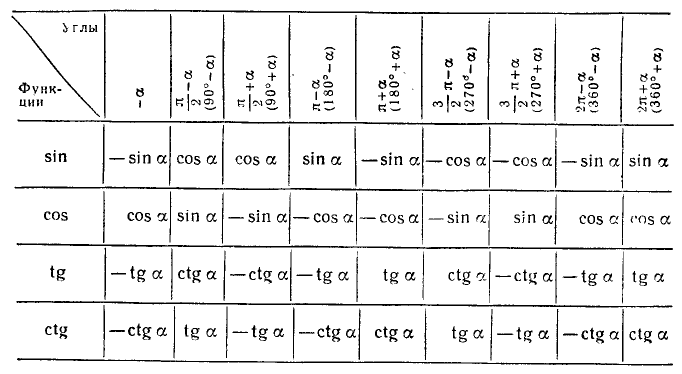
Объединим полученные для формул приведения результаты в следующую таблицу.
Для произвольного угла 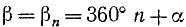
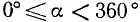
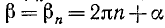
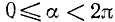

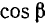
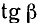
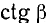
Пример:
Дан угол 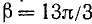

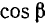
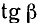
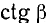
Решение:
Представим данный угол в виде 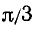
Заметим, что тангенс и котангенс можно было бы вычислить и так:
Пример:
Найти 
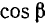
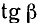
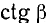
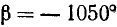
Решение:
Представим данный угол в виде
Применив формулы (104.1), получим
Тангенс и котангенс найдем следующим образом:
Пример:
Имеем угол 

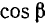
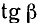
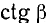
Решение:
Представим данный угол в виде
Применив формулы (104.1) и (106.1), получим
Пример:
Найти 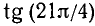
Решение:
Пример:
Найти 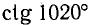
Решение:
Пример:
Решение:
Применив формулы приведения, получим в левой части предполагаемого тождества
т. е. левая часть равна 1. Мы пришли к верному равенству, что и доказывает наше тождество.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔥 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Что такое радиан?Скачать

Тригонометрические функции и их знакиСкачать

Синус, косинус произвольного угла. 9 класс.Скачать

Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать

ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать

Тригонометрическая окружностьСкачать