Собственные векторы и собственные значения неотрицательных матриц являются важными характеристиками функционирования экономических систем. Особое место среди неотрицательных матриц занимают неразложимые матрицы.
Определение 2.2. Матрица А называется неотрицательной (положительной) и обозначается А > О (А >0), если все ее элементы неотрицательны (положительны).
Определение 2.3. Неотрицательная квадратная (п х п)-матрицаА называется разложимой, если одновременной перестановкой строк и столбцов ее можно привести к виду
где 0 — нуль-матрица; аЛ| иЛ2 — квадратные матрицы размеров г х г и (« — г) х х (л — г) соответственно; в противном случае матрица называется неразложимой.
Замечание 2.4. Любая положительная матрица неразложима.
Замечание 2.5. С экономической точки зрения разложимость матрицы говорит о том, что в рамках данной экономической системы существует некоторая автономная подсистема. Так, если элемент a,j матрицы Л показывает, какое количество продукции /-й отрасли используется ву’-й отрасли, то разложимость матрицы А говорит о том, что существует группа отраслей, не использующих продукцию остальных отраслей. Неразложимость матрицы А показывает, что любая отрасль хотя бы косвенным образом использует продукцию всех отраслей.
Замечание 2.6. Квадратная матрица Л размера 2×2 разложима тогда и только тогда, когда либо а2 = 0, либо а2 = 0.
Действительно, если а2 = 0, то матрица Л уже приведена к виду (2.3). Если же аи = 0, то, меняя местами первую и вторую строку, а затем первый и второй столбец (т.е. перенумеровав индексы), мы приведем матрицу к виду (2.3).
Замечание 2.7. Из разложимости матрицы Л в общем случае не следует разложимость матрицы Л 2 . Так, например, матрица Л = 1 —
неразложима, а Л = ^ ^ J — разложима.
Теорема 2.1 (Фробениуса — Перрона). Неотрицательная матрица А имеет такое собственное значение ХА > 0, что ХА> |А.| для любого собственного значения X матрицы А. Кроме того, существует неотрицательный собственный вектор хА, соответствующий собственному числу ХА. Причем, если А неразложима, то ХА > 0 и существует хА >0.
Определение 2.4. Собственное значение ХА неотрицательной матрицы А называется Фробениусовым числом (числом Фробениуса), а собственный вектор хА > 0 — Фробениусовым вектором (вектором Фробениуса) матрицы А.
Пример 2.1. Пусть А = . Данная матрица неразложима. У нее
существуют два собственных значения: число Фробениуса ХА = 4 с собственным вектором хА = (2; 1)/ (он является вектором Фробениуса при t > 0) и собственное значение Х2 — —1, ему соответствует собственный вектор х = t (—2; 1) (/ ф 0). Очевидно, что ХА > (Х2).
Пример 2.2. Пусть А = . Данная матрица разложима. У нее
существуют два собственных значения: ХА = 3 — Фробениусово число, ему соответствует собственный вектор (хА > 0 при t > 0), и собственное значение Х2 = 1 с собственным вектором х = t (— 1; 1)(/*0).
Замечание 2.8. Так как собственные значения матриц Л и ^совпадают, то числа Фробениуса данных матриц равны.
Пусть рА — вектор Фробениуса матрицы А т , тогда
Транспонируя это равенство, мы получим (напомним, что в следующем равенстве (рА) т рассматривается как вектор-строка)
Поэтому весьма естественно говорить о векторах р/ и хЛ как соответственно о левом и правом векторах Фробениуса матрицы А.
Следствие 2.1. Если матрица А > 0 неразложима, то кроме вектора хА (определенного с точностью до положительного множителя) у нее нет других неотрицательных собственных векторов.
В самом деле, пусть существует вектор у > 0 такой, что Ау = Ху.
Тогда, умножив это равенство слева на (рА) Т , получим
Так как pj > 0, то р/ ? у > 0. Следовательно X = кА. То есть все неотрицательные собственные векторы будут соответствовать кА. Более того, в силу Теоремы Фробениуса — Перрона у > 0. Предположим, что векторы и у линейно независимы. Так как эти векторы определены с точностью до положительного множителя, то мы можем считать, что первая координата у них равна 1. Тогда вектор хА — у будет собственным вектором матрицы А, соответствующим ХА, но первая координата будет равна нулю, что противоречит Теореме Фробениуса — Перрона для неразложимой матрицы, следовательно, хА и у линейно зависимы, т.е. xA = ty 0).
Следствие 2.3. Пусть А> 0, тогда <),А) к является число Фробениуса А к .
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Теорема Фробениуса – Перрона. Число и вектор Фробениуса, их свойства
Теорема(Фробениуса-Перрона). Неотрицательная матрицаА имеет такое собственное значение 






Определение 1. Собственное значение 

Для определения числа Фробениуса 



Числа Фробениуса имеют ряд свойств, с которыми можно познакомиться в учебнике [2]. Одно из этих свойств дает простой способ определения числа Фробениуса матрицы: если все суммы элементов строк ( или столбцов) неотрицательной матрицы А равны одному и тому же числу 


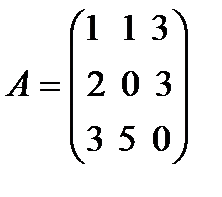
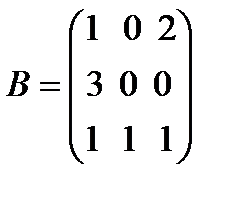
Тогда 

Число и вектор Фробениуса используются в балансовых экономических моделях и, в частности, в модели международной торговли [6]. Так, равновесный вектор национального дохода в модели международной торговли является вектором Фробениуса структурной матрицы международного обмена. Кроме того,
один из критериев продуктивности матрицы, которые будут рассмотрены ниже, формулируется в терминах числа Фробениуса[2].
4.2. Модель Леонтьева[6] многоотраслевой экономики
Эффективное функционирование экономики предполагает наличие баланса между отдельными отраслями экономической системы. Каждая отрасль при этом выступает, с одной стороны, как производитель некоторой продукции, а с другой, как потребитель продуктов, вырабатываемых другими отраслями.
Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции данной отрасли? Экономическая система, для которой применяется метод межотраслевого анализа, может быть большой (экономика страны) или малой (экономика региона или одного предприятия).
Для наглядного представления связи между отраслями экономической системы используют таблицы определенного вида, которые называют таблицами межотраслевого баланса (МОБ). Впервые эти таблицы были опубликованы в 1926 г. в СССР. Таблицы МОБ могут обеспечить органы власти и научно-исследовательские организации детализированной информацией о структурных пропорциях и межотраслевых связях в экономике страны, необходимой для прогнозирования и принятия решений в области экономической политики.
Различают отчетный и плановый межотраслевые балансы. Отчетный межотраслевой баланс отражает структуру производства и потребления продукции, произведенной в стране за отчетный год. Плановый межотраслевой баланс предназначен для планирования производства валового внутреннего продукта. В СССР такой план разрабатывался Госпланом и являлся директивным. В некоторых странах с рыночной экономикой, например, в Японии и Франции, такой план разрабатывается, но является индикативным, то есть не обязательным, а нацеливающим субъектов экономики на рациональные с точки зрения общества действия.
В советское время таблицымежотраслевого баланса разрабатывались в нашей стране на регулярной основе с 1959 по 1987 год. Первые плановые межотраслевые балансы в стоимостном и натуральном выражении были построены в 1962 г. Далее работы были распространены на республики и регионы. По данным за 1966 г. межотраслевые балансы были построены по всем союзным республикам и экономическим районам РСФСР. Последние базовые таблицы «затраты – выпуск» были разработаны за 1995 год. Дело в том, что номенклатуры отраслей и продукции в этих таблицах базировались на действующем в тот момент Общероссийском классификаторе отраслей народного хозяйства, который на сегодняшний день устарел.
14 февраля 2009 года, вышло распоряжение Правительства России №201-р, которое предписывало Росстату разработать базовые таблицы «затраты – выпуск» за 2011 год, в 2015 году представить их в Правительство Российской Федерации и осуществлять разработку базовых таблиц «затраты – выпуск» на регулярной основе 1 раз в 5 лет. Таблицы должны разрабатываться в соответствии с международными стандартами, изложенными в руководствах по составлению таблиц «затраты – выпуск» ООН и Евростата, и с учетом особенностей российской информационной базы.
Математическая модель межотраслевого баланса, допускающая широкие возможности анализа, планирования и прогнозирования хозяйственной деятельности, появилась в 1936 г. в трудах известного экономиста В.В. Леонтьева [6]. Предложенная Леонтьевым алгебраическая теория анализа «затраты – выпуск» сводилась ксистеме линейных уравнений, в которых параметрами были коэффициенты затрат на производство продукции. Леонтьев показал, что коэффициенты, выражающие отношения между секторами экономики (коэффициенты текущих материальных затрат), могут быть оценены статистически, что они достаточно устойчивы и их можно прогнозировать; обосновал существование наиболее важных коэффициентов, изменения которых необходимо отслеживать в первую очередь. Относительная простота измерений определила большие аналитические и прогностические возможности метода «затраты – выпуск».
Рассмотрим наиболее простой вариант модели межотраслевого баланса. Предположим, что весь производственный сектор народного хозяйства разбит на n чистых отраслей. Чистая отрасль – это условное понятие, которое определяет некоторую часть народного хозяйства, более или менее цельную (например, энергетика, машиностроение, сельское хозяйство и т.п.).
Пусть 



Единицы измерения всех указанных величин могут быть натуральными (кубометры, тонны, штуки и т.п.) или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Мы будем рассматривать стоимостной баланс.
В таблице 1 отражена принципиальная схема межотраслевого баланса в стоимостном выражении. Каждая отрасль представлена двояким образом: как элемент строки, она выступает в роли производителя продукции, а как элемент столбца – в роли потребителя продукции своей и других отраслей. Заметим, что таблица МОБ состоит из четырех частей (квадрантов), имеющих различное экономическое содержание.
Первый квадрант МОБ – это важнейшая часть межотраслевого баланса, содержащая информацию о межотраслевых связях.
Таблица 1 – Общая схема межотраслевого баланса производства и распределения продукции
| Производящие отрасли | Потребляющие отрасли | Итого | Конечный продукт | Валовой продукт | |||||
| … | j | … | n | ||||||
 |  | … |  | … |  |  |  |  | |
 |  | … |  | … |  |  |  |  | |
| … | … | … | … | … | … | … | … | … | … |
| i |  |  |  |  |  |  |  | ||
| … | … | … | I квадрант | … | … | II квадрант | |||
| n |  |  | … |  | … |  |  |  | 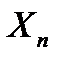 |
| Итого |  |  | … |  |  |  |  |  | |
| Условно чистая продукция |  |  | … |  | … |  |  | IV квадрант | |
| III квадрант | |||||||||
| Валовой продукт |  | 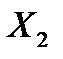 | … |  | … | 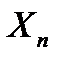 |  |
Основная часть этого квадранта представлена межотраслевыми поставками 

Второй квадрант состоит из двух столбцов. Первый из них – столбец конечной продукции всех отраслей 
Квадранты I иII отражают баланс между производством и потреблением.
Третий квадрант представлен двумя строками: строкой условно чистой продукции 

Первый и третий квадранты отражают стоимостную структуру продукции каждой отрасли (или стоимостную структуру национального дохода).
Четвертый квадрант непосредственного отношения к сфере производства не имеет, поэтому он не содержит никаких значений. По сути, этот квадрант должен отражать,как полученные в сфере материального производства первичные доходы населения (заработная плата, личные доходы и пр.), государства (налоги, прибыль и пр.), предприятий перераспределяются через различные каналы (финансово-кредитную систему, сферу обслуживания, общественно-политические организации и т.д.), в результате чего образуются конечные доходы населения, государства и т.д.
Переходим к построениюлинейной балансовой модели (ЛБМ) Леонтьева. Она представляет собой систему линейных уравнений, каждое из которых отражает равенство (баланс) между продукцией, производимой отдельной экономической отраслью, и совокупной потребностью в этой продукции во всей экономической системе.
Рассматривая схему МОБ по столбцам, можно сделать очевидный вывод, что сумматекущих производственных затрат любой потребляющей отрасли и ее условно чистой продукции равна валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:

Рассматривая схему МОБ по строкам для каждой производящей отрасли, можно видеть, что валовая продукция той или иной отрасли равна сумме текущего производственного потребления ее продукциивсеми отраслями и конечной продукции данной отрасли:

Просуммируем по всем отраслям системы (1) и (2), получим


Левые части двух равенств одинаковы, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей также равны. Как было отмечено ранее, это величинапромежуточного продукта экономической системы.Балансовый характер таблицы МОБ выражается в том, что из равенства уже обозначенных сумм вытекает очевидное равенство суммарной конечной и суммарной условно чистой продукции, то есть

Для получения ЛБМ продолжим работу с системой (2),представив ее в развернутом виде

Основу экономико-математической модели МОБ составляет матрица коэффициентов прямыхвнутрипроизводственных затрат (матрица технологическихкоэффициентов)А=(aij).
Определение 1. Коэффициенты прямых внутрипроизводственных затрат aijпоказывают, какое количество продукции i-ой отрасли необходимо (если учитывать только прямые затраты) для производства единицы валовой продукцииj-ой отрасли, то есть


Из равенства (3) получаем

Для получения значений 
1. Статистический. Коэффициенты 

2. Нормативный. Строится модель отрасли межотраслевого баланса. В этой модели отрасль рассматривается как совокупность отдельных производств, для каждого из которых уже разработаны нормативы затрат. Если заранее знать, какую продукцию будут выпускать производства отрасли, то по нормативам затрат можно рассчитать среднеотраслевые коэффициенты прямых затрат.
Заменив все межотраслевые поставки 
или в матричной форме
С помощью этой модели можно выполнять три вида плановых расчетов:
1. Задав в модели величины валовой продукции каждой отрасли Xi, можно определить объемы конечной продукции каждой отрасли Yiпо формуле
Y = (E — A) 
2. Задав величины конечной продукции всех отраслей Yi, можно определить величины валовой продукции каждой отрасли Xiпо формуле

3. Для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти недостающие величины конечной продукции первых отраслей и объемы валовой продукции вторых.
В формулах (7) и (8) Е обозначает единичную матрицу n-го порядка, а (Е – А) -1 обозначает матрицу, обратную к матрице (Е — А). Если определитель матрицы (Е — А)отличен от нуля, т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через 

Определение 2. Элементы матрицы 
Из экономического смысла векторов Х иYследует неотрицательность их координат. Вопрос о положительной разрешимости уравнения (6) зависит от свойств матрицы А. Плановые расчеты по модели Леонтьева можно выполнять, если матрица А является продуктивной.
Определение3. Неотрицательная матрицаА называется продуктивной, если существует такой неотрицательный вектор Х ³ 0, что
Неравенство (9) означает, что для выпуска каждого вида продукта потребуется затрат меньше, чем стоит сам продукт. Очевидно, что условие (9) означает существование положительного вектора конечной продукции 
Для того чтобы матрица коэффициентов прямых материальных затратА была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
1) матрица (Е — А) неотрицательно обратима, т.е. существует обратная матрицаВ=(Е – А) -1 , состоящая из неотрицательных элементов;
2) матричный рядЕ + А+ А 2 + А 3 + . = 

3) наибольшее по модулю собственное значение l матрицыА, то есть решение характеристического уравнения 
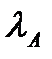
4) все главные миноры матрицы (Е – А), т.е. определители подматриц, образованных элементами первыхk строк и первых kстолбцов этой матрицы, порядка от 1 до п, положительны.
Рассмотрим другое определение коэффициентов полных материальных затрат, исходя из того, что кроме прямых затрат на получение той или иной продукции существуют косвенные затраты. Косвенные затраты относятся к предшествующим стадиям производства и входят в продукт не прямо, а через другие средства производства (см. рис. 1).
Определение 4. Коэффициентами полных материальных затрат 


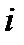

| Руда |
| Электро-энергия |
| Чугун |
| Электро-энергия |
| Сталь |
| Электро-энергия |
| Прокат |
| Косвенные затраты II порядка |
| Косвенные затраты I порядка |
| Прямые затраты |
Рисунок 1. Прямые и косвенные затраты на производство проката
Коэффициенты косвенных затрат связаны с коэффициентами прямых и полных затрат формулами

Примеры решения задач
Пример 1.Рассматривается двухотраслевая модель экономики, заданная балансовой таблицей
| Производящие отрасли | Потребляющие отрасли | Конечный продукт |
| Энергетика | Машиностроение | |
| Энергетика | ||
| Машиностроение |
1. Валовой выпуск продукции каждой отрасли 
2. Матрицу коэффициентов прямых внутрипроизводственных затрат А.
3. Построить линейную балансовую модель Леонтьева.
4. Матрицу коэффициентов полных затрат В.
5. Является ли матрицаА продуктивной? Для ответа на вопрос используйте хотя бы два критерия.
Все расчетные значения округлите до трех знаков после запятой.
1.Валовой выпуск продукции каждой отрасли определяем как сумму элементов каждой строки балансовой таблицы:
для энергетики –
для машиностроения –
2. Элементы матрицыАкоэффициентов прямых внутрипроизводственных затрат определяем по формуле






Таким образом, получаем матрицу коэффициентов прямых внутрипроизводственных затрат

3.Линейная балансовая модель Леонтьева имеет вид:
4.Матрицу коэффициентов полных затратВнаходим по формуле

где Е – единичная матрица второго порядка, т.е.





Далее действуем в соответствии с порядком определения обратной матрицы:
1) определитель
2) транспонированная матрица 
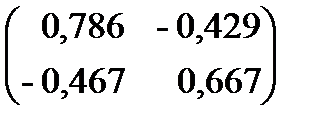
3) присоединенную матрицу получаем из алгебраических дополнений к элементам транспонированной, например, 

4) обратная матрица, т.е. матрица коэффициентов полных затрат


5.МатрицаА является продуктивной, так как выполняются, например, условия продуктивности 1 и 3:
1) обратная матрица (Е – А) -1 ³0, т.к. все ее элементы неотрицательны;
3) наибольшая из сумм элементов столбцов матрицыА равна 0,8, что меньше единицы.
Пример 2.Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям) и является конечным продуктом. Специалистами управляющей компании получены экономические оценки 

| Производящие отрасли | Коэффициенты прямых затрат  | Конечный продукт | |
| Отрасль 1 | Отрасль 2 | Отрасль 3 | |
| Отрасль 1 | 0,1 | 0,1 | 0,2 |
| Отрасль 2 | 0,1 | 0,2 | 0,3 |
| Отрасль 3 | 0,1 | 0,2 | 0,3 |
1. Проверить продуктивность технологической матрицы А=( 
2. Построить линейную балансовую модель Леонтьева и таблицу межотраслевого баланса производства и распределения продукции предприятий холдинга, определив для каждой отрасли валовой выпуск, межотраслевые поставки продукции, условно чистую продукцию.
Все расчетные значения округлите до трех знаков после запятой.
1.Проверка продуктивности технологической матрицы А=( 
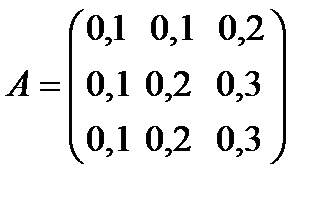
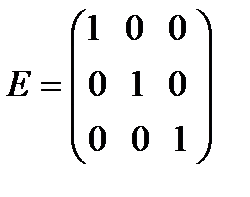


Вывод: так как все элементы матрицы 
2.Построение баланса производства и распределения продукции предприятий холдинга:
1) линейная балансовая модель Леонтьева имеет вид
2) валовой выпуск каждого предприятия находим по формуле

Выполняем умножение матриц



3) межотраслевые поставки продукции определяем по формуле

4) условно чистую продукцию находим из равенств

5) строим таблицу межотраслевого баланса
| Производящие отрасли | Потребляющие отрасли | Суммы | Конечный продукт | Валовой продукт | |
| Отрасль 1 | Отрасль 2 | Отрасль 3 | |||
| Отрасль 1 | 31,452 | 41,690 | 81,381 | 154,524 | 314,524 |
| Отрасль 2 | 31,452 | 83,381 | 122,071 | 236,905 | 416,905 |
| Отрасль 3 | 31,452 | 83,381 | 122,071 | 236,905 | 406,905 |
| Суммы | 94,357 | 208,452 | 325,524 | 628,333 | 1138,33 |
| Условно чистая продукция | 220,167 | 208,452 | 81,381 | ||
| Валовой продукт | 314,524 | 416,905 | 406,905 | 1138,33 |
Замечание. Баланс составлен правильно, еслиполучены следующие равенства:
1)Суммарное текущее производственное потребление равно суммарным текущим производственным затратам.Это промежуточный продукт экономической системы. В нашем случае он равен 628,333.
2) Суммарный конечный продукт равен суммарной условно чистой продукции.В нашем примере это общее значение равно 510 [10] .
Задачи для самостоятельного решения
Задание 1.Рассматривается многоотраслевая модель экономики, заданная балансовой таблицей.
1. Валовой выпуск продукции каждой отрасли 
2. Матрицу коэффициентов прямых внутрипроизводственных затрат А.
3. Построить линейную балансовую модель Леонтьева.
4. Матрицу коэффициентов полных затрат В.
5. Является ли матрицаА продуктивной? Для ответа на вопрос используйте хотя бы два критерия.
Все расчетные значения округлите до трех знаков после запятой.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Найти число и вектор фробениуса матрицы
чЕТОЕНУС Л ТБУУНПФТЕОЙА РТПУФЕКЫЕЗП ДЙОБНЙЮЕУЛПЗП БОБМПЗБ НПДЕМЙ мЕПОФШЕЧБ (0.4). лБЛ ВЩМП РПЛБЪБОП ТБОЕЕ (РТЙНЕТ 1.1), Ч НПДЕМЙ (0.4) ДПРХУФЙН ТЕЦЙН УВБМБОУЙТПЧБООПЗП ТПУФБ ЬЛПОПНЙЛЙ, ЕУМЙ НБФТЙГБ (pE — A) ОЕПФТЙГБФЕМШОП ПВТБФЙНБ ЙМЙ (УПЗМБУОП ФЕПТЕНЕ 2.1) РТПДХЛФЙЧОБ. рТЙ ЛБЛЙИ ЪОБЮЕОЙСИ РБТБНЕФТБ p ≥ 0 ЬФП ЧЕТОП? дМС ПФЧЕФБ ОБ ЬФПФ ЧПРТПУ ФТЕВХЕФ ЙЪХЮЕОЙС ЪБДБЮЙ П УПВУФЧЕООПН ЪОБЮЕОЙЙ ОЕПФТЙГБФЕМШОПК НБФТЙГЩ A ≥ 0
РТЙ ХУМПЧЙСИ 
фЕПТЕНБ 2.3 (ФЕПТЕНБ жТПВЕОЙХУБ-рЕТТПОБ). рХУФШA ≥ 0 — НБФТЙГБ (n × n) . фПЗДБ УРТБЧЕДМЙЧЩ УМЕДХАЭЙЕ ХФЧЕТЦДЕОЙС:
- УТЕДЙ УПВУФЧЕООЩИ ЮЙУЕМ НБФТЙГЩ A ЕУФШ ОЕПФТЙГБФЕМШОЩЕ ЧЕЭЕУФЧЕООЩЕ ЮЙУМБ Й ОБЙВПМШЫЕНХ ЙЪ ОЙИ λ(A) УППФЧЕФУФЧХЕФ ОЕПФТЙГБФЕМШОЩК УПВУФЧЕООЩК ЧЕЛФПТ
;
- НБФТЙГБ (pE — A) ОЕПФТЙГБФЕМШОП ПВТБФЙНБ ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ p > λ(A)
- ЕУМЙ ДМС ОЕЛПФПТПЗП ЧЕЭЕУФЧЕООПЗП ЮЙУМБ μ Й ЧЕЛФПТБ
ЧЩРПМОЕОП ОЕТБЧЕОУФЧП
, ФП μ ≥ λ(A);
- ЕУМЙ ω — УПВУФЧЕООПЕ ЮЙУМП НБФТЙГЩ A, ФП |ω| ≥ λ(A).
пРТЕДЕМЕОЙЕ 2.3.юЙУМП λ(A) ОБЪЩЧБЕФУС ЮЙУМПН жТПВЕОЙХУБ-рЕТТПОБ НБФТЙГЩ A, Б УППФЧЕФУФЧХАЭЙК ДБООПНХ ЮЙУМХ УПВУФЧЕООЩК ЧЕЛФПТ 
йЪ ФЕПТЕНЩ жТПВЕОЙХУБ-рЕТТПОБ УМЕДХЕФ, ЮФП ДМС УХЭЕУФЧПЧБОЙС ДПРХУФЙНЩИ ТЕЦЙНПЧ УВБМБОУЙТПЧБООПЗП ТПУФБ Ч НПДЕМЙ (0.4) ОЕПВИПДЙНП Й ДПУФБФПЮОП ЮФПВЩ p > λ(A) , Ф.Е., ХЮЙФЩЧБС ЧЧЕДЕООЩЕ ТБОЕЕ ПВПЪОБЮЕОЙС, ФЕНР ТПУФБ ЬЛПОПНЙЛЙ s < 1/λ(A).
фБЛЙН ПВТБЪПН, ДМС ПГЕОЛЙ ДПРХУФЙНЩИ ФЕНРПЧ ТПУФБ Ч ДЙОБНЙЮЕУЛПК НПДЕМЙ мЕПОФШЕЧБ ОЕПВИПДЙНП ЧЩЮЙУМЙФШ ЮЙУМП жТПВЕОЙХУБ-рЕТТПОБ НБФТЙГЩ A , Ф.Е. ТЕЫЙФШ ЪБДБЮХ ОБ УПВУФЧЕООЩЕ ЪОБЮЕОЙС (0.8). дМС ЬФПЗП НПЦОП ЧПУРПМШЪПЧБФШУС ЙФЕТБГЙПООЩН НЕФПДПН, ДПЛБЪБФЕМШУФЧП ЛПФПТПЗП НПЦОП ОБКФЙ Ч МЙФЕТБФХТЕ РП ЮЙУМЕООЩН НЕФПДБН Ч МЙОЕКОПК БМЗЕВТЕ (УН. ОБРТЙНЕТ, [3]).
йФЕТБФЙЧОХА РТПГЕДХТХ ТЕЫЕОЙС ЪБДБЮЙ (0.8) ОБЪЩЧБАФ УФЕРЕООЩН НЕФПДПН ЧЩЮЙУМЕОЙС ЮЙУМБ Й ЧЕЛФПТБ жТПВЕОЙХУБ-рЕТТПОБ. оЙЦЕ РТЙЧЕДЕО РПДТПВОЩК БМЗПТЙФН РТЙНЕОЕОЙС УФЕРЕООПЗП НЕФПДБ.
🎬 Видео
Собственные векторы и собственные значения матрицыСкачать

А.7.35 Собственные вектора и собственные значения матрицыСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

7 4 Собственные векторы и собственные значенияСкачать

Собственные значения и собственные векторыСкачать

Матрицы и векторыСкачать

Что такое векторы и матрицы? Душкин объяснитСкачать

Лекция №2.2 НормыСкачать

Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать

Как разложить вектор по базису - bezbotvyСкачать

Матрицы: начало. Высшая математикаСкачать

11. Ранг матрицыСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

8 5 Теорема Фробениуса Перрона и ее приложенияСкачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Линал 2.6. Умножение матрицы на векторСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать











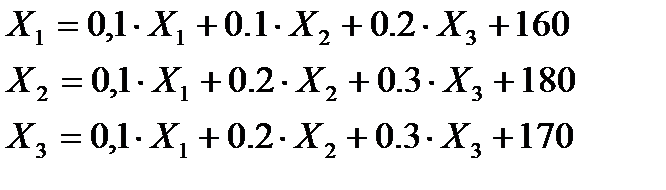



 ЧЩРПМОЕОП ОЕТБЧЕОУФЧП
ЧЩРПМОЕОП ОЕТБЧЕОУФЧП  , ФП μ ≥ λ(A);
, ФП μ ≥ λ(A);