- Nav view search
- Navigation
- Search
- Проекции вектора. Направляющие косинусы. Неравенство Коши-Буняковского.
- Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
- Проекции вектора. Направляющие косинусы.
- Неравенство Коши-Буняковского.
- Векторное произведение векторов.
- Формулы вычисления векторного произведения векторов
- Свойства векторного произведения векторов
- Примеры задач на вычисления векторного произведения векторов
- Векторное произведение векторов онлайн
- Предупреждение
- Векторное произведение векторов
- Геометрические свойства векторного произведения векторов
- Векторное произведение векторов в декартовых координатах
- Векторное произведение векторов на примерах
- 🎥 Видео
Видео:№919. Выпишите координаты векторов а =2 i +3j , b = -½i -2j , с =8i , d = i - j , e =-2j , f=-i .Скачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра.
- Высшая математика.
- Векторная алгебра.
- Проекции вектора. Направляющие косинусы. Неравенство Коши-Буняковского
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Проекции вектора. Направляющие косинусы. Неравенство Коши-Буняковского.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Проекции вектора. Направляющие косинусы.
Проекцией вектора $a$ на вектор $b$ называется число $Pr_b a=|a|cosvarphi,$ где $varphi=widehat$ угол между векторами $a$ и $b,$ $0leqvarphileqpi.$
Координаты $X, Y, Z$ вектора $a$ в прямоугольном базисе совпадают с проекциями вектора $a$ на базисные орты $i, j, k$ соответственно, а длина вектора $a$ равна $|a|=sqrt.$
$$cosgamma=coswidehat=frac<sqrt>,$$ называются направляющими косинусами вектора $a.$
Направляющие косинусы совпадают с координатами (проекциями) его орта $a_0=frac.$
Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Неравенство Коши-Буняковского.
Для любых векторов евклидова пространства справедливо неравенство Коши-Буняковского $$|(x, y)|^2leq(x, x)(y, y).$$
2.35. Заданы векторы $a_1(-1; 2; 0),$ $a_2(3; 1; 1)$ $a_3(2; 0; 1)$ и $a=a_1-2a_2+1/3a_3.$ Вычислить:
а) $|a_1|$ и координаты орта $a_$ вектора $a_1;$
б) $coswidehat;$
в) координату $X$ вектора $a;$
г) $Pr_j a.$
Решение.
в) $a=2 a_1-2a_2+1/3a_3=(-1; 2; 0)-2(3; 1; 1)+1/3(2; 0; 1)=$ $=(-1; 2; 0)+(-6; -2; -2)+(2/3; 0; 1/3)=(-19/3; 0; -5/3).$
г) $Pr_j a=a_y=0.$
в) $a_x=-19/3;$
г) $Pr_j a=0.$
2.40. Найти координаты орта $a_0,$ если $a(6; 7; -6).$
Решение.
Ответ: $left(frac, frac, -fracright).$
2.45. Найти вектор $x,$ образующий с ортом $j$ угол $pi/3,$ с ортом $k -$ угол $2pi/3,$ если $|x|=5sqrt.$
Решение.
Пусть $x=(x_1, x_2, x_3).$ Тогда
Далее находим $x_1:$
2.39. Заданы векторы $a=2i+3j, b=-3j-2k, c=i+j-k.$ Найти
а) координаты орта $a_0;$
б) координаты вектора $a-1/2b+c;$
в) разложение вектора $a+b-2c$ по базису $B=(i, j, k);$
б) $a-fracb+c=d(3, 11/2, 0);$
в) $a+b-2c=-2j;$
г) $Pr_j (a-b)=6.$
2.42. Найти длину и направляющие косинусы вектора $p=3a-5b+c$ если $a=4i+7j+3k; b=i+2j+k; c=2i-3j-k.$
Видео:Координаты вектора. 9 класс.Скачать

Векторное произведение векторов.
 |
| рис. 1 |
Видео:№403. Запишите координаты векторов: a = 3i+2j—5k, b=—5i + 3k — k, c=i — j, d = j+k, mСкачать

Формулы вычисления векторного произведения векторов
Векторное произведение двух векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Свойства векторного произведения векторов
| SΔ = | 1 | | a × b | |
| 2 |
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Примеры задач на вычисления векторного произведения векторов
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i (2 · (-2) — 3 · 1) — j (1 · (-2) — 2 · 3) + k (1 · 1 — 2 · 2) =
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i (2 · (-1) — (-2) · 1) — j ((-1) · (-1) — (-2) · 2) + k ((-1) · 1 — 2 · 2) =
Из свойств векторного произведения:
SΔ = 1 2 | a × b | = 1 2 √ 0 2 + 5 2 + 5 2 = 1 2 √ 25 + 25 = 1 2 √ 50 = 5√ 2 2 = 2.5√ 2
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Координаты точки и координаты вектора 1.Скачать

Векторное произведение векторов онлайн
Данный онлайн калькулятор вычисляет векторное произведение векторов. Дается подробное решение. Для вычисления векторного произведения векторов введите координаты векторов в ячейки и нажимайте на кнопку «Вычислить.»
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Show that vectors a and b are parallelСкачать

Векторное произведение векторов
Прежде, чем перейти к определению векторного произведения векторов, рассмотрим понятия упорядоченная тройка векторов, левая тройка векторов, правая тройка векторов.
Определение 1. Три вектора называются упорядоченой тройкой (или тройкой ), если указано, какой из этих векторов первый, какой второй и какой третьий.
Запись cba — означает — первым является вектор c, вторым является вектор b и третьим является вектор a.
Определение 2. Тройка некомпланарных векторов abc называется правой ( левой ), если при приведении к общему началу, эти векторы располагаются так, как расположены соответственно большой, несогнутый указательный и средний пальцы правой(левой) руки.
Определение 2 можно формулировать и по другому.
Определение 2′. Тройка некомпланарных векторов abc называется правой ( левой ), если при приведении к общему началу, вектор c располагается по ту сторону от плоскости, определяемой векторами a и b, откуда кратчайший поворот от a к b совершается против часовой стрелки (по часовой стрелке).
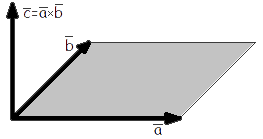
Тройка векторов abc, изображенная на рис. 1, является правой, а тройка abc изображенная на рис. 2, является левой.
  |
Если две тройки векторов являются правыми либо левыми, то говорят, что они одной ориентации. В противном случае говорят, что они противоположной ориентации.
Определение 3. Декартовая или афинная система координат называется правой ( левой ), если три базисных вектора образуют правую (левую) тройку.
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Определение 4. Векторным произведением вектора a на вектор b называется вектор с, обозначаемый символом c=[ab] (или c=[a,b], или c=a×b) и удовлетворяющий следующим трем требованиям:
- длина вектора с равна произведению длин векторов a и b на синус угла φ между ними:
|c|=|[ab]|=|a||b|sinφ; (1) - вектор с ортогонален к каждому из векторов a и b;
- вектор c направлен так, что тройка abc является правой.
Векторное произведение векторов обладает следующими свойствами:
- [ab]=−[ba] ( антиперестановочность сомножителей);
- [(λa)b]=λ[ab] ( сочетательность относительно числового множителя);
- [(a+b)c]=[ac]+[bc] ( распределительность относительно суммы векторов);
- [aa]=0 для любого вектора a.
Видео:A=2i-3j-k and B=i+4j-2k. Find AXBСкачать

Геометрические свойства векторного произведения векторов
Теорема 1. Для коллинеарности двух векторов необходимо и достаточно равенство нулю их векторного произведения.
Доказательство. Необходимость. Пусть векторы a и b коллинеарны. Тогда угол между ними 0 или 180° и sinφ=sin180=sin 0=0. Следовательно, учитывая выражение (1), длина вектора c равна нулю. Тогда c нулевой вектор.
Достаточность. Пусть векторное произведение векторов a и b навно нулю: [ab]=0. Докажем, что векторы a и b коллинеарны. Если хотя бы один из векторов a и b нулевой, то эти векторы коллинеарны (т.к. нулевой вектор имеет неопределенное направление и его можно считать коллинеарным любому вектору).
Если же оба вектора a и b ненулевые, то |a|>0, |b|>0. Тогда из [ab]=0 и из (1) вытекает, что sinφ=0. Следовательно векторы a и b коллинеарны.
Теорема 2. Длина (модуль) векторного произведения [ab] равняется площади S параллелограмма, построенного на приведенных к общему началу векторах a и b.
Доказательство. Как известно, площадь параллелограмма равна произведению смежных сторон этого параллелограмма на синус угла между ними. Следовательно:
| S=|[ab]|=|a||b|sinφ. | (2) |
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Векторное произведение векторов в декартовых координатах
Теорема 3. Пусть два вектора a и b определены своими декартовыми прямоугольными координатами
| a=<x1, y1, z1>, b=<x2, y2, z2>. |
Тогда векторное произведение этих векторов имеет вид:
| [ab]=<y1z2—y2z1, z1x2−z2x1, x1y2−x2y1>. | (3) |
Для запоминания формулы (3) удобно представить векторное произведение векторов в виде определителя:
 |
Раскрывая определитель по элементам первой строки мы получим разложение вектора a×b по базису i, j, k, которое эквивалентно формуле (3).
Доказательство теоремы 3. Составим все возможные пары из базисных векторов i, j, k и посчитаем их векторное произведение. Надо учитывать, что базисные векторы взаимно ортогональны, образуют правую тройку и имеют единичную длину (иными словами можно предполагать, что i=, j=, k=). Тогда имеем:
 | (4) |
    |
Из последнего равенства и соотношений (4), получим:
  |
которая эквивалентна равенству (3).
Видео:9 класс, 2 урок, Координаты вектораСкачать

Векторное произведение векторов на примерах
Пример 1. Найти векторное произведение векторов [ab], где
 , ,  . . |
Составим 3×3 матрицу, первая строка которой базисные векторы i, j, k, а остальные строки заполнены элементами векторов a и b:
 . . |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов a и b:
   . . |
Таким образом, результатом векторного произведения векторов a и b будет вектор:
 . . |
Пример 2. Найти векторное произведение векторов [ab], где вектор a представлен двумя точками. Начальная точка вектора a: 


Р е ш е н и е. Переместим первый вектор на начало координат. Для этого вычтем из соответствующих координат конечной точки координаты начальной точки:
 . . |
Составим 3×3 матрицу, первая строка которой базисные векторы i, j, k, а остальные строки заполнены элементами векторов a и b:
 . . |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов a и b:
   . . |
Таким образом, результатом векторного произведения векторов a и b будет вектор:
🎥 Видео
Найдите разложение вектора по векторам (базису)Скачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

#ProductOfVectors For what values of λ, the vectors i – λj + 2k and 8i + 6j – k are right anglesСкачать

Координаты в новом базисеСкачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

The angle between the two vectors A=i+2j-k and B=-i+j-2k isСкачать