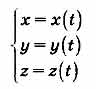Положение точки с помощью радиуса вектора (3 видео)

Способы задания положения точки и описание ее движения — Кинематика — МЕХАНИКА

1.1. Кинематика

1.1.5. Способы задания положения точки и описание ее движения

Положение точки в пространстве задается двумя способами:

1) с помощью координат; 2) с помощью радиус-вектора.

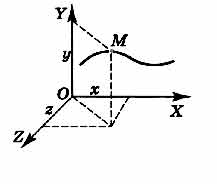
Положение точки с помощью координат задается тремя проекциями точки х, у, z на оси декартовой системы координат ОХ, ОУ, ОZ, связанные с телом отсчета (рис. 1.3). Для этого из точки А необходимо опустить перпендикуляры на плоскости УZ (координата х), ХZ (координата у), ХУ (координата z) соответственно. Записывается это так: А (х, у, z). Для конкретного случая, изображенного на рис. 1.3 (х = 6, у = 10, z = 4,5), точка А обозначается A (6; 10; 4,5).

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси (х на ось ОХ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат О и лежащая на диагонали параллелепипеда, и будет искомой точкой А.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: ОХ и ОУ. Тогда положение точки на плоскости определяют двумя координатами х и у (рис. 1.4).

Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.

Задание положения точки А с помощью радиус-вектора осуществляется соединением точки А с началом координат О (рис. 1.4). Направленный отрезок О А = называется радиус-вектором.

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций rх, ry, rz на оси координат ОХ, ОУ, OZ, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 1.4) имеем:

Здесь r = | — модуль радиус-вектора , х и y — его проекции на оси координат, все три величины — скаляры; х и у — координаты точки А.

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор г можно также разложить на составляющие по осям X и У, т. е. представить в виде суммы двух векторов (рис. 1.4):

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус- вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).

Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называетсяпрямолинейным, а если кривая — криволинейным.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

Содержание

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.
Кинематика. Задание положения точки.
Векторный способ задания положения точки .
📽️ Видео

Видео:Радиус векторСкачать

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

ПОСОБЫ ОПИСАНИЯ ДВИЖЕНИЯ

«Физика — 10 класс»

Какими величинами можно описать механическое движение тела?

Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчёта.

Существует несколько способов описания, или, что одно и то же, задания движения точки. Рассмотрим два из них, которые наиболее часто применяются.

Будем задавать положение точки с помощью координат. Если точка движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.

Математически это принято записывать в виде

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме.

Если уравнения движения известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и её положение относительно выбранного тела отсчёта. Вид уравнений для каждого конкретного движения будет вполне определённым.

Основной задачей кинематики является определение уравнения движения тел.

Количество выбираемых для описания движения координат зависит от условий задачи. Если движение точки происходит вдоль прямой, то достаточно одной координаты и, следовательно, одного уравнения, например, x(t). Если движение происходит на плоскости, то его можно описать двумя уравнениями — x(t) и y(t). Уравнения описывают движение точки в пространстве.

Векторный способ.

Положение точки можно задать, и с помощью радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину), т. е. является функцией времени:

= (t)

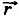
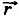
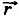
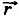
На рисунке радиус-вектор ₁ определяет положение точки в момент времени t₁, а радиус-вектор ₂ — в момент времени t₂.

Выше приведенная формула и есть уравнение движения точки, записанное в векторной форме. Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение. Задание трёх скалярных уравнений равносильно заданию одного векторного уравнения.

Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором. Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось? Изобразим ось ОХ.

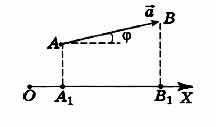
Опустим из начала А и конца В вектора 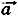перпендикуляры на ось ОХ. Точки А₁ и В₁ есть проекции соответственно начала и конца вектора на эту ось.

Проекцией вектора на какую-либо ось называется длина отрезка А₁ В₁ между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «—». Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ах и ау — проекции вектора на оси координат ОХ и OY. Согласно определению проекции вектора на ось можно записать: ах = ± |А₁ В₁|.

Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.

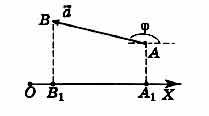
Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций. В противном случае она считается отрицательной.

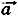
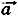
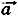
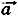
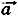
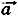
Проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ. Иногда нужно находить составляющие вектора, например векторы x, и y. Сумма составляющих равна вектору :

= x + y.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.