Диаграмма треугольника в электротехнике

Цепь трехфазного тока может содержать в себе различные компоненты. Для ее стабильной работы, необходимо правильно рассчитать все напряжения, нагрузки и иные параметры. Статья даст подробное описание, что такое векторная диаграмма для трехфазной цепи, опишет ее разновидности, способы расчета.

Видео:Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

Определение

Векторной диаграммой называют метод графического изображения расчета всех параметров цепи переменного тока в виде векторов. Данный метод предполагает изображение всех составных напряжений, токов и процессов в виде отложенных векторов на плоскости.

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Назначение

Векторная диаграмма используется для расчетов напряжений, токов в трехфазной цепи и других цепях переменного тока. Метод помогает определить значение всех процессов, происходящих в схеме, их влияние на каждый проводник, нейтраль, а также провести расчет возникающих нагрузок.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Разновидности

Векторные диаграммы трехфазных сетей могут быть симметричными или несимметричными. Построение гистограммы прямо зависит от ее схемы. Разновидности цепей и их гистограмм описаны далее в статье.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Симметричные

Симметричные цепи переменного тока предполагают соединение 3 фаз от источника (генератора) с тремя приемниками.

При этом создаются совершенно независимые трехфазные схемы. При этом используется соединение трех фаз генератора звездой. Для симметричных схем должны соблюдаться требования:

1. Амплитуда должна быть для всех фаз одинаковой.
2. ЭДС должна иметь угол сдвига 120 градусов.
3. Угловые частоты должны быть равными.

Также учитывается принцип чередования ЭДС во времени. Если ротор генератора вращается по часовой стрелке (правое вращение), то происходит чередование прямого типа (A, B, C). Такая система считается симметричной.

Если ротор вращается против часовой стрелки (левое вращение), чередование считается обратным (A, C, B), но общая система ЭДС остается все так же симметричной.

Для симметричных схем применяется расчет по векторной гистограмме, приведенной ниже.

Видео:Векторная диаграммаСкачать

Несимметричные

Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:

1. Увеличение сопротивления нейтрали.
2. Полное отсутствие проводимости.
3. Увеличение напряжения.
4. Максимальное искажение фазных напряжений.

При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.

Ниже приведена векторная диаграмма несимметричной цепи.

Видео:Векторная диаграмма при соединении приемника треугольникомСкачать

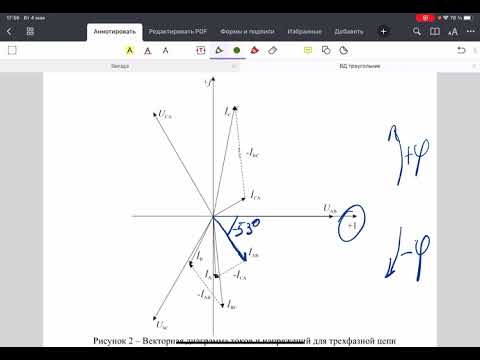
Построение диаграммы

Векторная диаграмма предполагает в своей основе следующие значения:

1. Точку начала отсчета N для всех трех отдельных фаз.
2. Векторное направление ABC как отдельных проводников источника напряжения (генератора). Каждый вектор имеет заданную длину, равную своему напряжению.
3. Окончание векторов AВ, BС, CА, как приемников напряжения.

Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.

А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.

Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.

Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.

Видео:Соединение трехфазных цепей звездой и треугольникомСкачать

Заключение

Если вы работаете с трехфазными цепями, то векторная диаграмма используется для получения визуального отображения всех действующих процессов в таких цепях переменного трехфазного тока. Такая диаграмма полезна при определении несоответствий схемы между углами сдвига фаз, напряжениями и токами.

Видео:Векторная диаграмма - как она строится без чисел по схемеСкачать

Видео по теме

Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Соединение потребителей электрической энергии в треугольник

При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:

Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть U_Ф = U_Л. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.

На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.

В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:

Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.

Видео:Расчет Трехфазной цепи Без комплексных чисел. Соединение треугольникомСкачать

Симметричная нагрузка при соединении приемников треугольником

В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:

Очевидно, что при симметричной нагрузке:

Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:

В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения U_ab принято направлять вертикально вверх.

Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):

На основании данной векторной диаграммы можно записать: . Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке .

Пример

Трехфазная сеть имеет линейное напряжение U_Л = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное r_ф = 8,65 Ом и индуктивное x_ф = 5 Ом сопротивления.

Решение

Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.

Линейные и фазные токи, а также полные сопротивления фаз будут равны:

Активная, реактивная и полная мощности электроприемника любой фазы будут равны:

Векторные диаграммы приведены выше.

Видео:Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Несимметричная нагрузка при соединении приемников треугольником

В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:

В пределах каждой группы подключение приемников производится параллельно.

После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:

Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:

Для определения суммарной мощности всех фаз нужно применять выражение:

Пример

Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: U_Л = 220 В, r_ab = 40 Ом, x_Lbc = 10 Ом, r_bс = 17,3 Ом, x_cа = 5 Ом, r_Ccа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.

Решение

Воспользовавшись выражением для определения комплексных значений получим:

Комплексные значения полных сопротивлений фаз: Z_ab = 40 Ом, Z_bс = 17,3 + j10 Ом, Z_bс = 8,65 – j5 Ом.

Комплексные и действующие значения линейных и фазных токов:

Дольше можно проводить расчеты, не прибегая к комплексному методу:

Общие активные и реактивные мощности:

Углы сдвига между токами и напряжениями:

Векторная диаграмма для несимметричного треугольника приводилась выше.

Видео:Векторные диаграммы и коэффициент мощностиСкачать

Треугольник мощностей электротехника это

Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать

Треугольник напряжений, полная мощность

В электрической цепи, приведенной на рис. 2.6, элементы r,
L
и
С
соединены последовательно и подключены к источнику синусоидального напряжения. Ток в этой цепи изменяется по синусоидальному закону.

Уравнение электрического состояния цепи для мгновенных значений напряжений имеет вид

Уравнение электрического состояния может быть записано так же, как сумма векторов напряжений, т.е. вектор напряжения на входе цепи равен сумме векторов напряжений на элементах r,
L
и
С
:

Сравнивая правые части уравнений электрического состояния, записанные для мгновенных значений и в виде векторов, видно, что напряжение Ur

на элементе
r
совпадает по фазе с током, напряжение
UL
на элементе
L
опережает ток на угол , напряжение
UC
на элементе
С
отстает от тока на угол . Уравнение в виде суммы векторов можно представить как геометрическую сумму векторов на векторной диаграмме. Построение векторной диаграммы начинают с вектора тока , так как при последовательном соединении
r,L
и
С
он является общим для всех элементов в цепи (рис. 2.7).

Направим вектор тока по горизонтальной оси (см. рис. 2.7). Векторы напряжений на участках строятся на условиях обхода контура против направления тока. Вектора напряжений направляются в сторону возрастающего потенциала.

Потенциал точки 0 приравнивается к нулю, вектор совпадает с вектором тока и направлен от точки 0

к точке
с.
Напряжение на элементе
L
опережает ток на угол , вектор строится из точки
с
к точке
b
под углом к вектору тока (см. рис. 2.7). Напряжение на элементе
С
отстает от тока на угол , следовательно, вектор необходимо направить в сторону отставания, т.е. на диаграмме из точки
b
вниз до точки a
(UС Читайте также:

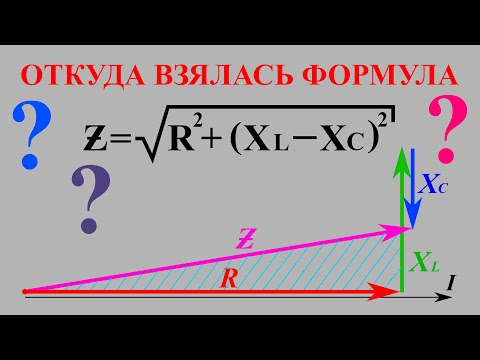
раз уменьшенные стороны треугольника напряжений (рис. 2.8).

Рис. 2.8. Треугольник сопротивлений

Из треугольника сопротивлений можно определить угол сдвига фаз φ

между током и напряжением:
.
В электротехнике принято обозначать угол φ

стрелкой, направленной от вектора тока к вектору напряжения. Знак угла
φ
в выражении для мгновенного значения тока
i
определяется характером нагрузки: при индуктивном характере нагрузки (
xL>xС
) ток отстает от напряжения на угол
φ
, и в выражении для мгновенного тока угол
φ
записывается со знаком минус: ; при емкостном характере нагрузки (
xL Читайте также: Формула «чужого» сопротивления

Активная мощность всегда положительна.

Реактивная мощность, определяющая обмен энергией между цепью и источником питания, находится из формулы

Реактивная мощность может быть положительной при индуктивном характере нагрузки (xL>
xС
) или отрицательной при емкостном режиме (
xL Читайте также: Как выбрать электрика для замены проводки и не быть обманутым?

Так как по построению векторы U

а и
U
р в сумме равны
U
, то из выражений (1) и (2) вектор напряжения на входе двухполюсника можно представить как

Разделим выражение (3) на модуль вектора тока

Выражение (4) соответствует представлению на комплексной плоскости вектора Z

, равного комплексному сопротивлению двухполюсника и развернутого относительно вещественной оси на угол y
i
. При этом вектор
Z
e
jφ
e
jy i
=
Z
e
j
(y
u- y i
+y
i
)=
Z
e
jy u
образует с вещественной осью комплексной плоскости угол y
u
, т.е. оказывается совпадающим по направлению с вектором
U
.

Сравнивая вещественные и мнимые части выражений (3) и (4), можно представить модули составляющих вектора U

т.е. модуль составляющей U

а , называемой
активной или резистивной составляющей напряжения на входе двухполюсника
, представляет собой падение напряжения на резистивной составляющей его комплексного сопротивления при токе
I
. Аналогично, модуль вектора
U
р , называемого
реактивной составляющей входного напряжения
, является падением напряжения на реактивной составляющей комплексного сопротивления.

Рассмотренным соотношениям величин соответствует представление двухполюсника последовательным соединением резистора R

и реактивного сопротивления
X
, представленным на рис. 1 а).

Таким образом, вектор падения напряжения на входе двухполюсника может быть представлен двумя составляющими, одна из которых является его проекцией на направление вектора входного тока и называется активной (резистивной) составляющей или активным падением напряжения. Активная составляющая соответствует падению напряжения на резистивном сопротивлении последовательной эквивалентной схемы двухполюсника. Вторая составляющая перпендикулярна вектору тока и соответствует падению напряжения на реактивном сопротивлении последовательной эквивалентной схемы.

Прямоугольные треугольники U
U
а
U
р и
ZRX
(рис. 1 а)) подобны и называются соответственно
треугольниками напряжений и сопротивлений
.

Спроектируем теперь вектор тока I

на направление вектора падения напряжения
U
(рис. 1 б)). Длина проекции будет равна
I
а=
I
cosφ , а длина проектирующего перпендикуляра —
I
р=
I
sinφ . Представим эти отрезки векторами с учетом того, что
I
а совпадает с направлением вектора падения напряжения на входе двухполюсника, а в сумме эти два вектора должны быть равны
I
. Тогда в показательной форме —

является оператором поворота отрезка
I
р на 90° в направлении отставания, чтобы обеспечивалось условие
I
а +
I
р =
I
.

Представим теперь вектор тока через полученные составляющие

Разделим выражение (8) на модуль вектора U

Таким образом, из прямоугольного треугольника, составленного из векторов I

а,
I
р и
I
и описанного выражением (8), делением на постоянную величину
U
всех его сторон мы получили подобный треугольник, описываемый выражением (9). Стороны нового треугольника имеют размерность проводимости и связаны с составляющими вектора тока законом Ома

Следовательно, активную и реактивную составляющую вектора тока можно представить, в виде токов, протекающих через активную (резистивную) проводимость G

и реактивную проводимость
B
эквивалентной параллельной схемы двухполюсника (рис. 1 б)).

Прямоугольные треугольники I
I
а
I
р и
YGB
(рис. 1 б)) подобны и называются соответственно
треугольниками токов и проводимостей
. Очевидно, что треугольники токов и проводимостей подобны треугольникам напряжений и сопротивлений, т.к. имеют одинаковые углы.

Обобщая понятия составляющих векторов тока и напряжения на входе двухполюсника, можно сделать следующие выводы:

• активная (резистивная) и реактивная составляющие вектора напряжения на входе двухполюсника соответствуют падениям напряжения на резистивном и реактивном сопротивлениях последовательной эквивалентной схемы (схемы R-X);
• активная (резистивная) и реактивная составляющие вектора тока на входе двухполюсника соответствуют токам, протекающим через резистивную и реактивную проводимости параллельной эквивалентной схемы (схемы G-B);
• понятиями активной и реактивной составляющих тока и напряжения можно пользоваться, не связывая их с какой-либо эквивалентной схемой двухполюсника, т.к. из подобия треугольников напряжений, токов, сопротивлений и проводимостей следует взаимно однозначная связь этих величин.

что, как не тужатся релятивисты, CMB (космическое микроволновое излучение) — прямое доказательство существования эфира, системы абсолютного отсчета в космосе, и, следовательно, опровержение Пуанкаре-эйнштейновского релятивизма, утверждающего, что все ИСО равноправны, а эфира нет. Это фоновое излучение пространства имеет свою абсолютную систему отсчета, а значит никакого релятивизма быть не может. Подробнее читайте в FAQ по эфирной физике.

Видео:Зачем нужны векторные диаграммы?Скачать

Способы компенсации

Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.

Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.

На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.

Видео:Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Треугольник мощностей

Треугольник мощностей представляет собой прямоугольный треугольник, показывающий соотношение между активной, реактивной и полной мощностью.
Когда каждая составляющая тока (активная составляющая (Icosϕ) или реактивная составляющая (Isinϕ)) умножается на напряжение U, получается треугольник мощности, показанный на рисунке ниже:

Мощность, которая фактически потребляется или используется в цепи переменного тока, называется активной мощностью или реальной мощностью. Она измеряется в ваттах (Вт), киловаттах (кВт) или МВт.

Мощность, которая протекает в линиях переменного тока, но не выполняет полезной работы, называется реактивной мощностью. Реактивная мощность измеряется в вольт-амперах (ВАр) реактивных, киловольт-амперах реактивных (кВАр) или МВАр.

Произведение среднеквадратичного значения напряжения и тока известно как полная мощность. Она измеряется в вольт-амперах (ВА), кВА или МВА.

Следующий пункт показывает взаимосвязь между электрическими величинами и объясняется графическим представлением под названием треугольник мощностей, показанным выше.

• Когда активная составляющая тока умножается на напряжение цепи U, получается активная мощность. Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром.
• Когда реактивная составляющая тока умножается на напряжение цепи, получается реактивная мощность. Она определяет коэффициент мощности сети . Она не выполняет полезную работу, а только перегоняется по сети, создавая препятствия для полезной мощности.
• Когда общий ток цепи (активный и реактивный) умножается на напряжение — мы получаем полную мощность.

Коэффициент мощности (cos φ) может быть определен из треугольника мощностей путем вычисления отношений активной мощности к полной:

Как мы знаем, обычная мощность означает произведение напряжения и тока, но в цепи переменного тока, за исключением чисто резистивной нагрузки, обычно существует разность фаз между напряжением и током, и поэтому произведение напряжения и тока не отражает реальной или активной мощности в цепи.

Видео:Как работает пусковой переключатель со звезды на треугольникСкачать

Что такое реактивная мощность?

Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.

Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.

Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.

При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.

Видео:Построение векторной диаграммы. Цепь RLCСкачать

Треугольник мощностей и cos φ

Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.

Применяя теорему Пифагора, вычислим модуль вектора S:

Отсюда можно найти реактивную составляющую:

Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают P f. Таким образом, P f = cos φ = P/S.

Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.

Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).

Из этого можно сделать вывод: чем ближе к 1 коэффициент P f , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.

Видео:7. Решение задачи на трехфазные цепи по схеме треугольника.Скачать

Нужны ли устройства компенсации в быту?

На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:

• электрочайник (P f = 1);
• лампы накаливания (P f = 1);
• электроплита (P f = 1) и другие нагревательные приборы;

Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.

Но если речь идёт о холодильнике (P f = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.

Экономический эффект от установки таких устройств ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15% средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не электроэнергию.

Попутно вы решите следующие вопросы:

• уменьшение нагрузок на индуктивные элементы и на проводку;
• улучшение качества тока, способствующего стабильной работе электронных устройств;
• понижение уровня высших гармоник в бытовой сети.

Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.

📹 Видео

Как снять векторную диаграммуСкачать

Лекция 25. Преобразование звезды в треугольник.Скачать