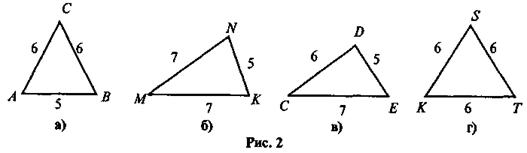О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Определение равнобедренного треугольника
- Признаки равнобедренного треугольника
- Свойства равнобедренного треугольника
- Примеры решения задач
- Интересные факты о треугольниках. Мини-учебник для учащихся и преподавателей.
- Описание презентации по отдельным слайдам:
- Интересные факты про равнобедренный треугольник
- Задачи урока
- План урока
- Равнобедренный треугольник
- Виды равнобедренных треугольников
- Свойства равнобедренного треугольника
- Домашнее задание
- Интересные факты
- 🎬 Видео
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
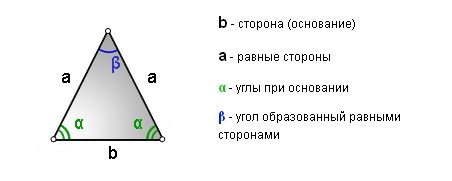
| Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
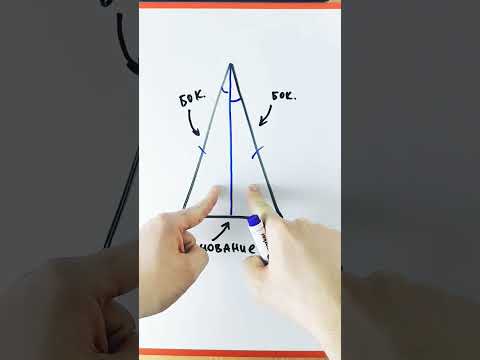
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Видео:Все свойства равнобедренного треугольника за минутуСкачать
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Видео:7 фактов про равносторонний треугольникСкачать

Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Видео:Как распознать равнобедренный треугольник? #shortsСкачать

Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Интересные факты о треугольниках. Мини-учебник для учащихся и преподавателей.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Мини-учебник Треугольники Учитель математики Меньшикова С.В.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Интересные факты В Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Содержание — Проверь себя — Тесты — Терминологический словарь выход Интересные факты Виды треугольников Педальный треугольник Практическая часть
В герметической идеографии треугольник с устремленной к верху вершиной, символизирует огонь и отвечает идее вознесения, духовности, красному цвету. Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь, соответствующий синему цвету. Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею; зеленый цвет. Треугольник воздуха с горизонтальной чертой символизирует Землю, неподвижную стоячую воду и соответствует черному цвету.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы. Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу — Отца, Сына и Святого Духа.
Светящаяся Дельта — это равнобедренный треугольник (с углом 108° на вершине и двумя углами по 36° у основания), в середине которого расположены Божественный Глаз (видимое Солнце, дающее Свет и Жизнь, Логос, Творческое начало) или священная Тетраграмма I E V Е, имя Бога, которое иудейский первосвященник произносил лишь один-единственный раз в году. Его три стороны являют собой выражение формулы: правильно думать, правильно говорить, правильно делать, или лозунг: Свобода, Равенство, Братство. Начало
Прямоугольным называется тот треугольник, у которого один из углов прямой. Сторона, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол, называются катетами. Начало
Тогда Перепишем последнее равенство в таком виде: Из этой пропорции следует, что треугольники DBC и DCP подобны. Значит, . Получаем: и AB=BC. Доказательство. Так как подобен , то AD:BD=PD:AD, и AD=DC. Теорема 1. Если точка Брокара Р есть точка пересечения медиан, то треугольник АВС правильный. BD=DC∙√3 и BD2 = DC2. 3.
Доказательство. Так как ВР=АР, то отрезок РМ в треугольнике АВР служит медианой, так и высотой. Теорема 2. Если точка Брокара Р является пересечением медианы СМ с биссектрисой АЕ, то треугольник правильный. Но тогда отрезок СМ в треугольнике АВС также служит высотой и медианой, а значит и биссектрисой, следовательно, точка Р – пересечение биссектрис, и треугольник АВС правильный.
Следовательно, треугольник АМР подобен треугольнику СМА и угол МАР равен углу МСА, а значит и AB=BC, Р – точка пересечения медиан, т.е. треугольник АВС правильный. Доказательство. Из подобия треугольников МВР и МСВ следует, что МВ:МС=МР:МВ или МВ2=МС.МР, но по условию МВ=МА, тогда МА2=МС.МР и МА:МС=МР:МА. Теорема 3. Если точка Брокара Р является точкой пересечения медианы СМ с высотой ВD, то треугольник АВС правильный.
В равнобедренном треугольнике АРC высота PD является и медианой, т.е. AD=DC. Следовательно, высота BD в треугольнике АВС является и медианой. Точка Брокара Р в треугольнике АВС является пересечением биссектрисы СМ с медианой BD, отсюда, по предыдущей теореме, треугольник АВС правильный. Доказательство. Так как Р – точка Брокара, то и (СМ является биссектрисой в треугольнике АВС). Отсюда следует, что в треугольнике АРС стороны АР и РС равны. Теорема 4. Если точка Брокара Р является точкой пересечения биссектрисы СМ с высотой BD, то треугольник АВС правильный. Начало
Сложив, получим , а так как Sa+Sb+Sc=S, то . Следствие. В равностороннем треугольнике сумма расстояний от произвольной точки, взятой внутри треугольника, до его сторон есть величина постоянная, равная высоте треугольника. Имеем: . 2) Если из точки L внутри треугольника опущены перпендикуляры соответственно на стороны а, b, с треугольника, то . la, lb, lc, Дано: треугольник АВС, а, b, с – стороны треугольника АВС, – педальная точка, la, lb, lc – перпендикуляры от L, ha, hb, hc – высоты треугольника АВС. Доказать: Треугольник АВС разобьется на три треугольника. Назовем площади этих треугольников Sa, Sb, Sc.
Доказательство: т.к. OL, OM, ON – перпендикуляры, то AO2-AL2=BO2-BL2 или Сложив эти три равенства, получим: AL2-BL2+BM2-MC2+CN2-NA2=0 или AL2+BM2+CN2=BL2+MC2+NA2. 3) Перпендикуляры, опущенные их точки, лежащей в плоскости треугольника, на его стороны, определяют на сторонах шесть отрезков так, что сумма квадратов трех отрезков, не имеющих общих концов, равна сумме квадратов других трех отрезков. Дано: треугольник АВС, OL, OM, ON — перпендикуляры. Доказать: AL2+BM2+CN2=LB2+MC2=AN2
Доказательство: Если соединить точки А и Р, то получим двойники: одна — при вершине В1, а другая при вершине С1, далее при вершинах С2 и В2 и , наконец, обе – при вершине А3. Следовательно, треугольник АВС и треугольник имеют равные углы при вершинах А и А3. Аналогично, они имеют равные углы В и В3. таким образом, теорема доказана. Дано: АВС, Р – педальная точка. Доказать: подобен 4) Третий педальный треугольник подобен исходному.
Вычисление площади педального треугольника. Тогда SА1В1С1= SС1МВ1 + SA1MB1= SA1MC. Так как данный треугольник и треугольник С1МВ1 отличается тем свойством, что ^A + ^ M = π, то SС1МВ1/ S= С1М* МВ1 / c* b; SС1МВ1 = S*С1М* МВ1 / c* b. Так как С1М= 2S*сn-1/(an + bn +cn), МВ1= 2S*bn-1/(an + bn +cn), A1M= 2S*an-1/(an + bn +cn), то SА1В1С1= 4S3 * сn-1* bn-1/(an + bn +cn)2* c* b= 4S3 * сn-2* bn-2/(an + bn +cn)2 . Определив аналогично площади треугольников A1M В1 и A1M С1 и сложив полученные значения, найдём площадь педального треугольника: SА1В1С1= 4S3 *(bn-2cn-2 + cn-2an-2 + an-2bn-2)/ (an + bn +cn)2 . Задача решена. Пусть М- точка пересечения прямых n, т.е. прямых, делящих стороны треугольника пропорционально n-м степеням прилежащих сторон, и А1С1В1– медальный треугольник точки М .
Площадь педального треугольника центра тяжести. т.е. n=0. Тогда SА1В1С1= 4S3 *(b-2c-2 + c-2a-2 + a-2b-2)/ 9. SА1В1С1= 4/9S3 * (a2 + b2 + c2)/ a2* b2* c2. Задача решена. По определению медиан: АК=КС, следовательно: АК/ КС=с0/а0,…
Площадь педального треугольника центра вписанной окружности. По свойству биссектрисы в треугольнике: АК/ КС=с/а,… т.е. n = 1. Тогда SА1В1С1= 4S3 *(1/bc + 1/ca + 1/ab)/ (a + b +c)2 =4S3 *(a + b + c)/2р*a* b* c= = 2 S3 *р/ р2*a* b* c=2 S3/ р*a* b* c= 4S2*r/2a* b* c= S*r/2R. Задача решена.
Площадь педального треугольника точки пересечения высот. По свойству высот в треугольнике: АВ1/В1С = с2/а2,… Таким образом, n=2. Тогда SА1В1С1=4S3 *3/ (a2 + b2 + c2)2= 12 S3/ (a2 + b2 + c2)2. Задача решена. Начало
Решение: Ответ: 7,5 (см) Задача 1 Вычислить стороны педального треугольника, если расстояния от педальной точки до вершин треугольника х=4см, у=5см, z=6см, R=12 см, а стороны самого треугольника равны 8 см, 12 см, 15 см. Шаблон для создания презентаций к урокам математики. Савченко Е.М.
Дано: АВС – равносторонний, la=1,5 см, lb=2,8 см, lc=1,7 см. Найти: Решение: Т.к. треугольник равносторонний, то la+lb+lc=h, т.е. h=1,5+2,8+1,7=6 (см). Пусть ВD=х, АВ=36+х2=4х2 , 36=3х2 , х2=12, (см2) Ответ. 12 (см2) . Задача 2 Расстояния от точки треугольника, взятой внутри равностороннего треугольника АВС, до сторон АВ, ВС, АС равны соответственно 1,7 см, 2,8 см, 1,5 см. Найти площадь этого треугольника. Шаблон для создания презентаций к урокам математики. Савченко Е.М.
Дано: треугольник АВС; OL, OM и ON — перпендикуляры , АВ=9, АС=12 Найти: ВС Решение: Т.к. , а АВ=9, то AL=3, LB=9, аналогично, AN=3, NC=12. По теореме о сумме отрезков AL2+BM2+CN2=BL2+MC2+AN2 , 9+64+144=81+МС2+9, МС2=127, МС= , ВС=8+ (см) Ответ: 8+ (см) Задача 3 Перпендикуляры, опущенные из точки О, взятой внутри треугольника АВС, определяют на сторонах треугольника точки L, M, N так, что , причем . Известно, что АВ=9, АС=12. Найдите сторону ВС. Шаблон для создания презентаций к урокам математики. Савченко Е.М.
Решение. (см2) Ответ: 1,57 (см2) Задача 4 Найти площадь педального треугольника точки Брокара, если стороны треугольника равны 4, 7 и 5 см. Шаблон для создания презентаций к урокам математики. Савченко Е.М.
Решение. Ответ: Задача 5 Определите угол Брокара, если треугольник имеет следующие стороны 3, 2 и 5.
Решение. В прямоугольном треугольнике DCB , поэтому, воспользовавшись формулой и подставив в нее это равенство, получаем: . Выполним преобразования: где 2sinAsinC=cos(C-A)-cos(C+A). Подставив в формулу это значение, получаем: Подставив значения косинуса угла В, получим: Учитывая, что , находим: В первом случае: Во втором случае: Задача 6 В треугольнике АВС и точка Брокара Р лежит на высоте CD. Найдите отношение : Начало
Три точки, образующие треугольник, называются Вершинами треугольника Точками Брокара Сторонами треугольника Главными точками
Стороны треугольника образуют в вершинах треугольника Три угла плоскость Угол отрезок
Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри треугольника, называется педальным равносторонним равнобедренным разносторонним
Точкой Брокара называется точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы Точка пересечения медиан треугольника центр окружности главная точка
Если точка Брокара является точкой пересечения медиан, то треугольник правильный равнобедренный Не существуют прямоугольный
Если расстояние от педальной точки до вершины треугольника АВС равны х, у, z, то длины сторон педального треугольника равны Между собой 1 R
Видео:Свойства равнобедренного треугольника #огэ #математика #shortsСкачать

Интересные факты про равнобедренный треугольник
• Познакомить учеников с равнобедренным треугольником;
• Продолжать формировать навыки построения прямоугольных треугольников;
• Расширить знания школьников о свойствах равнобедренных треугольников;
• Закрепить теоретические знания при решении задач.
Видео:Равнобедренный треугольник. 7 класс.Скачать

Задачи урока
• Уметь формулировать, доказывать и использовать теорему о свойствах равнобедренного треугольника в процессе решения задач;
• Продолжать развитие сознательного восприятия учебного материала, логического мышления, навыков самоконтроля и самооценки;
• Вызвать познавательный интерес к урокам математики;
• Воспитывать активность, любознательность и организованность.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

План урока
1. Общие понятия и определения о равнобедренном треугольнике.
2. Свойства равнобедренного треугольника.
3. Признаки равнобедренного треугольника.
4. Вопросы и задания.
Видео:✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать

Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, имеющий две равные стороны, которые называются боковыми сторонами равнобедренного треугольника, а его третья сторона называется основанием.
Вершиной данной фигуры есть та, которая расположена напротив его основания.
Угол, который лежит напротив основания называется углом при вершине этого треугольника, а два других угла называются углами при основании равнобедренного треугольника.
Видео:Геометрия 7 класс (Урок№32 - Повторение. Равнобедренный треугольник и его свойства.)Скачать

Виды равнобедренных треугольников
Равнобедренный треугольник, как и другие фигуры, может иметь разные виды. Среди равнобедренных треугольников встречаются остроугольные, прямоугольные, тупоугольные и равносторонние.
• Остроугольный треугольник имеет все острые углы.
• У прямоугольного треугольника угол его вершины прямой, а при основании расположены острые углы.
• Тупоугольный имеет тупой угол при вершине, а при его основании углы острые.
• У равностороннего все его углы и стороны равны.
Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Свойства равнобедренного треугольника
• Противолежащие углы в отношении равных сторон равнобедренного треугольника, равны между собой;
• Биссектрисы, медианы и высоты, проведённые из углов, противолежащих равным сторонам треугольника, равны между собой.
• Биссектриса, медиана и высота, направлена и проведена к основанию треугольника, совпадают между собой.
• Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, (они совпадают) проведенных к основанию.
• Противолежащие равным сторонам равнобедренного треугольника углы, всегда острые.
Данные свойства равнобедренного треугольника применяются при решении задач.
Видео:Полезные факты про равносторонний треугольник.Скачать

Домашнее задание
1. Дайте определение равнобедренного треугольника.
2. В чем особенность этого треугольника?
3. Чем отличается равнобедренный треугольник от прямоугольного?
4. Назовите известные вам свойства равнобедренного треугольника.
5. Как вы думаете, можно ли на практике проверить равенство углов при основании и как это сделать?
А теперь давайте проведем небольшой блиц-опрос и узнаем, как вы усвоили новый материал.
Послушайте внимательно вопросы и ответьте верно ли такое утверждение, что:
1. Треугольник можно считать равнобедренным, если у него две стороны равны?
2. Биссектрисой называют отрезок, который соединяет вершину треугольника с серединой противоположной стороны?
3. Биссектрисой является отрезок, который делит угол, который соединяет вершину с точкой противоположной стороны пополам?
Советы относительно решения задач о равнобедренном треугольнике:
1. Для определения периметра равнобедренного треугольника достаточно умножить длину боковой стороны на 2 и сложить это произведение с длиной основы треугольника.
2. Если в задаче известны периметр и длина основы равнобедренного треугольника, то для нахождения длины боковой стороны достаточно отнять длину основы от периметра и найденную разницу разделить на 2.
3. А чтобы найти длину основы равнобедренного треугольника, зная и периметр, и длину боковой стороны, необходимо всего лишь умножить боковую сторону на два и отнять это произведение от периметра нашего треугольника.
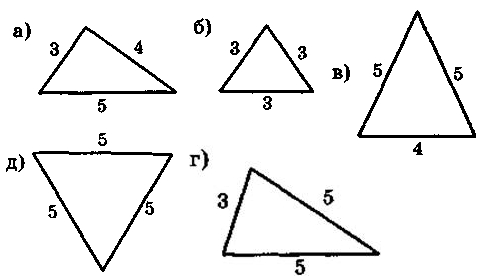
1. Среди треугольников на рисунке определите один лишний и объясните свой выбор:
2. Определите, какие из изображенных на рисунке треугольников являются равнобедренными, назовите их основы и боковые стороны, а так же рассчитайте их периметр.
3. Периметр равнобедренного треугольника равен 21 см. Найдите стороны этого треугольника, если одна из них больше на 3 см. Какое количество решений может иметь данная задача?
4. Известно, что если боковая сторона и противолежащий основе угол одного равнобедренного треугольника равен боковой стороне и углу другого, то эти треугольники будут равны. Докажите это утверждение.
5. Подумайте и скажите, является ли любой равнобедренный треугольник равносторонним? И будет ли любой равносторонний треугольник равнобедренным?
6. Если стороны равнобедренного треугольника равны 4 м и 5 м, то каков будет его периметр? Сколько решений может иметь эта задача?
7. Если один из углов равнобедренного треугольника равен 91 градусу, то чему равны остальные углы?
8. Подумайте и ответьте, какие углы должны быть у треугольника, чтобы он одновременно был и прямоугольным, и равнобедренным?
Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Интересные факты
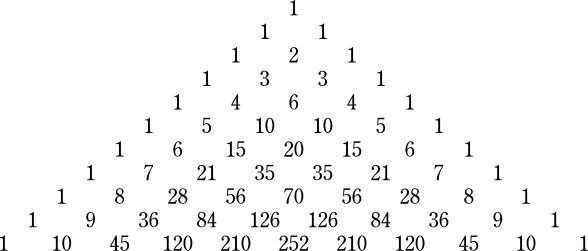
А кто из вас знает, что такое треугольник Паскаля? Задачку на построение треугольника Паскаля часто задают для проверки навыков элементарного программирования. Вообще треугольник Паскаля относиться к комбинаторике и теории вероятности. Так что же это за такой треугольник?
Треугольник Паскаля — это бесконечный арифметический треугольник или таблица в форме треугольника, которая сформирована при помощи биномиальных коэффициентов. Простыми словами, вершиной и сторонами этого треугольника являются единицы, а сам он заполнен суммами двух чисел, которые расположены выше. Складывать такой треугольник можно до бесконечности, но если его очертить, то мы получим равнобедренный треугольник с симметричными строками относительно его вертикальной оси.
Подумайте, а где в повседневной жизни вам приходилось встречать равнобедренные треугольники? Не правда ли, крыши домов и древних архитектурных сооружений очень напоминают их? А вспомните, какая основа у египетских пирамид? Где еще вам встречались равнобедренные треугольники?
Равнобедренные треугольники с древних времен выручали греков и египтян при определении расстояний и высот. Так, например, древние греки определяли с его помощью издалека расстояние до корабля в море. А древние египтяне определяли высоту своих пирамид благодаря длине отбрасываемой тени, т.к. она представляла собой равнобедренный треугольник.
Начиная с древних времен, люди уже тогда оценили красоту и практичность этой фигуры, так как формы треугольников нас окружают всюду. Передвигаясь по разным селениям, мы видим крыши домов и других сооружений, которые напоминают нам о равнобедренном треугольнике, зайдя в магазин, мы нам встречаются пакеты с продуктами и соками треугольной формы и даже некоторые человеческие лица имеют форму треугольника. Эта фигура настолько популярна, что ее можно встретить на каждом шагу.
🎬 Видео
Равнобедренный треугольник и его свойстваСкачать

Равнобедренный треугольникСкачать

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Равнобедренный треугольник и его свойства . 7 классСкачать

Геометрия 7 класс - равнобедренный треугольник и его свойстваСкачать
Равносторонний треугольник в окружностиСкачать

Вещдок (HD): расследование дела "Равнобедренный треугольник"Скачать