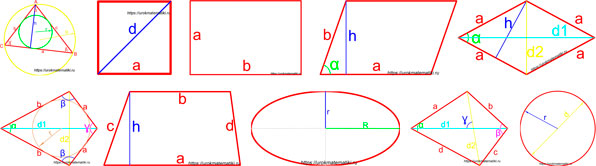
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
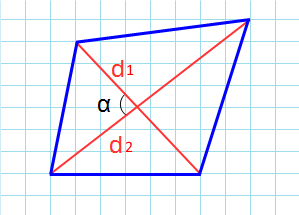
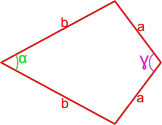
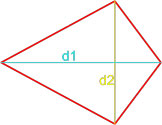
- Через диагонали и угол между ними
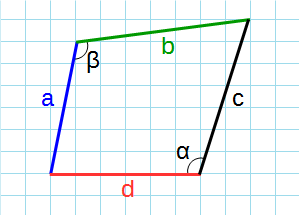
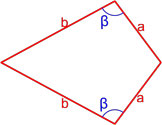
- Через стороны и противолежащие углы
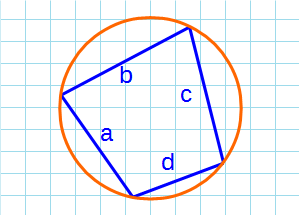
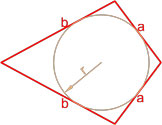
- Площадь вписанного четырехугольника в окружность
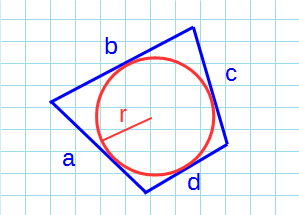
- Площадь описанного четырехугольника около окружности через радиус
- Площадь круга: как найти, формулы
- Определение основных понятий
- Формула вычисления площади круга
- Площадь круга через радиус
- Площадь круга через диаметр
- Площадь круга через длину окружности
- Задачи. Определить площадь круга
- Формулы площадей фигур
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
- Формула площади ромба по длине стороны и углу
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
- Формула площади трапеции по длине основ и высоте
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
- Формула площади вписанного четырехугольника (формула Брахмагупты)
- Формула площади четырехугольника с вписанной окружностью
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- 💥 Видео
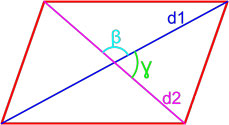
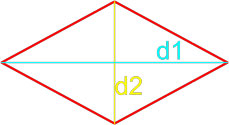
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
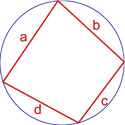
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
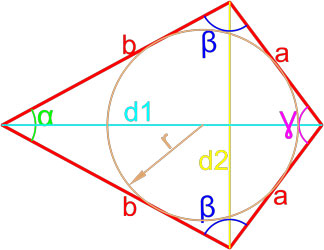
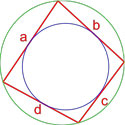
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
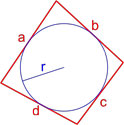
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Видео:№1116. Найдите площадь круга, описанного около: а) прямоугольника со сторонами а и bСкачать
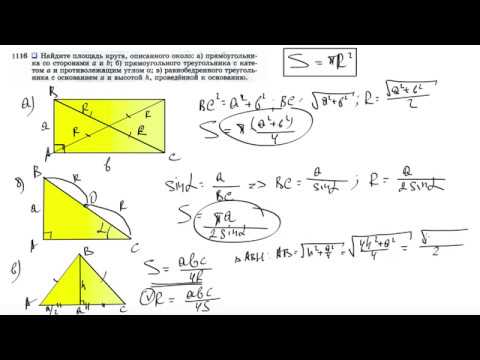
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Видео:КАК НАЙТИ ПЛОЩАДЬ КРУГА, ОПИСАННОГО ОКОЛО КВАДРАТА? Примеры | ГЕОМЕТРИЯ 9 классСкачать

Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
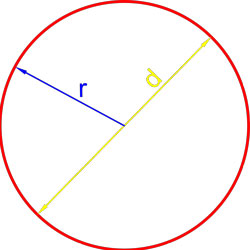
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Видео:Площадь круга. Математика 6 класс.Скачать

Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Видео:Лучший способ найти площадь кругаСкачать

Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Найти центр кругаСкачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
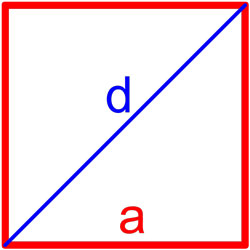
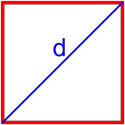
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Площадь круга. 9 класс.Скачать

Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
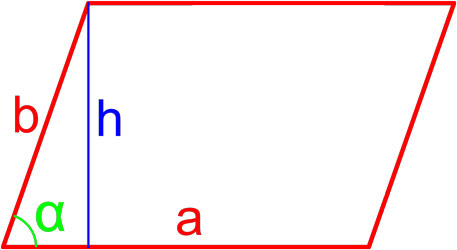
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы площади ромба
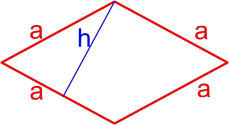
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
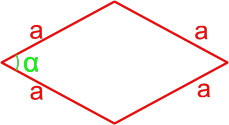
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
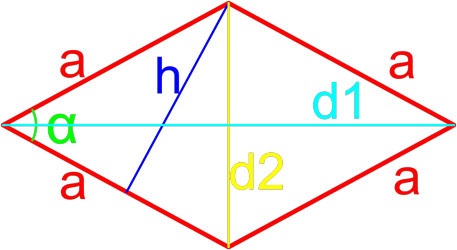
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:площадь круга вписанного и описанного вокруг треугольника решение задачСкачать

Формулы площади трапеции
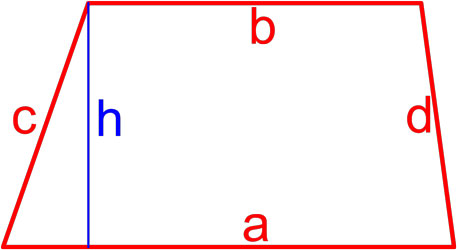
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
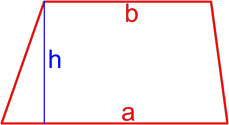
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Видео:Геометрия Найдите площадь круга, описанного около равнобедренного треугольника, если основание этогоСкачать

Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Видео:Найдите площадь кругаСкачать

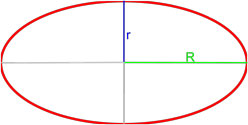
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
💥 Видео
Задача 3 ЕГЭ по математике. Урок 84Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Длина окружности. Практическая часть. 9 класс.Скачать