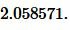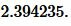- Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
- Ваш ответ
- решение вопроса
- Похожие вопросы
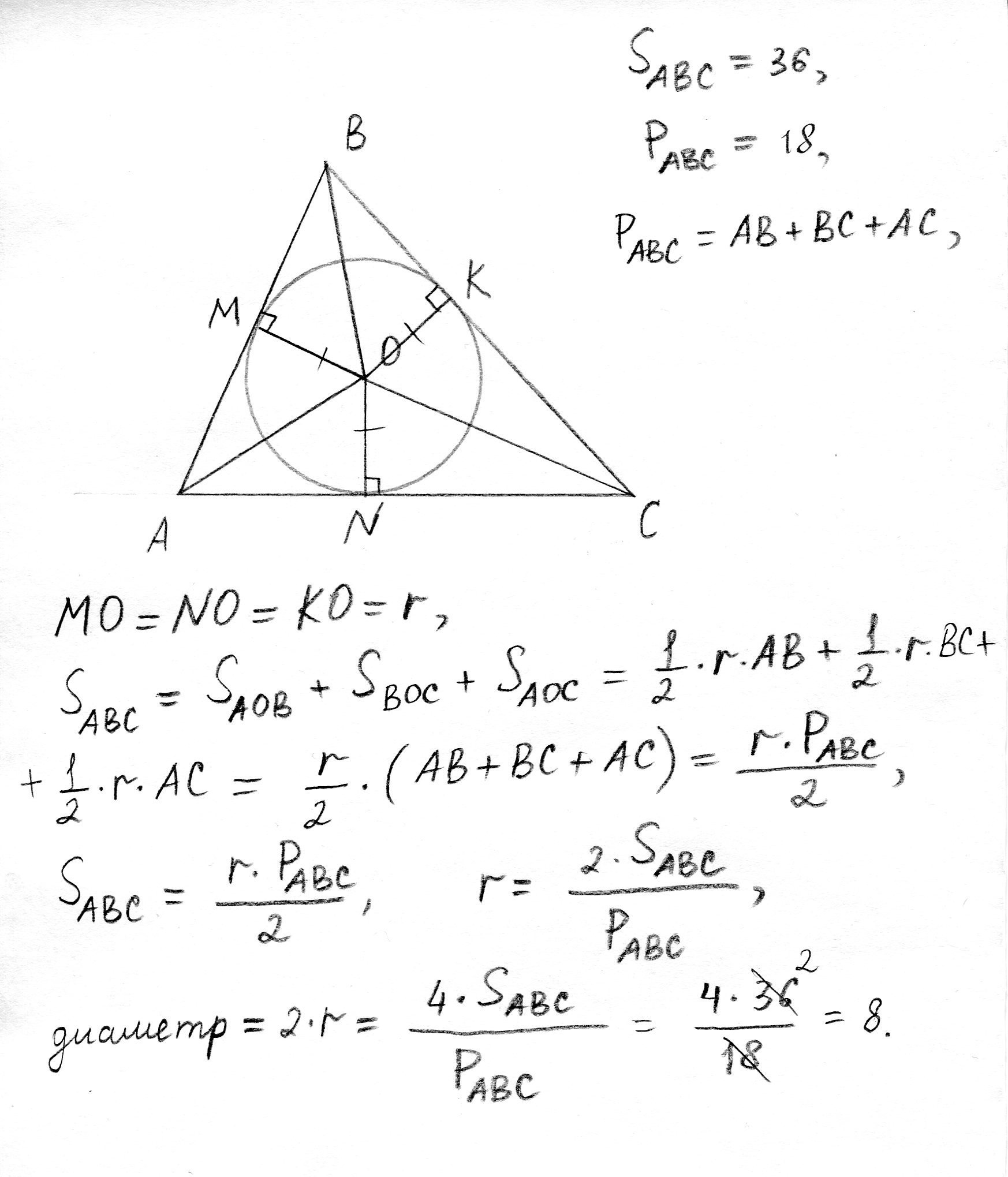
- Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник?
- Площадь треугольника равна 130 , а его периметр равен 52?
- Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см?
- Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см?
- В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см ?
- Диаметр окружности описанной около правильного треугольника, равен 12корню из трех?
- Длина окружности, вписанной в правильный треугольник, равна 12П см?
- Радиус окружности, вписанной в правильный треугольник, равен корень из трех?
- Точки T и P соответственно середины сторон BC и AC — треугольника ABC?
- В прямоугольный треугольник вписана окружность?
- В прямоугольный треугольник вписана окружность?
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник?
- Площадь треугольника равна 130 , а его периметр равен 52?
- Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см?
- Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см?
- В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см ?
- Диаметр окружности описанной около правильного треугольника, равен 12корню из трех?
- Длина окружности, вписанной в правильный треугольник, равна 12П см?
- Радиус окружности, вписанной в правильный треугольник, равен корень из трех?
- Точки T и P соответственно середины сторон BC и AC — треугольника ABC?
- В прямоугольный треугольник вписана окружность?
- В прямоугольный треугольник вписана окружность?
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Ваш ответ
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

решение вопроса
Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник?
Геометрия | 10 — 11 классы
Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник.
Я решил на листочке, прикрепил который.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Площадь треугольника равна 130 , а его периметр равен 52?
Площадь треугольника равна 130 , а его периметр равен 52.
Найдите радиус вписанной в треугольник окружности.
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см?
Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см.
Вычислите диаметр окружности, вписаной в треугольник.
Видео:Окружность, вписанная в треугольникСкачать

Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см?
Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см.
Вычислите радиус окружности, вписанной в треугольник ABC, если известно , что площадь треугольника ABT равна 9 см2.
Видео:Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см ?
В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см .
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Диаметр окружности описанной около правильного треугольника, равен 12корню из трех?
Диаметр окружности описанной около правильного треугольника, равен 12корню из трех.
Вычислите периметр этого треугольника.
Видео:ОГЭ Задача 26 Радиусы вписанных окружностей в подобных треугольникахСкачать

Длина окружности, вписанной в правильный треугольник, равна 12П см?
Длина окружности, вписанной в правильный треугольник, равна 12П см.
Найдите периметр этого треугольника.
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Радиус окружности, вписанной в правильный треугольник, равен корень из трех?
Радиус окружности, вписанной в правильный треугольник, равен корень из трех.
Найдите периметр и площадь треугольника.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Точки T и P соответственно середины сторон BC и AC — треугольника ABC?
Точки T и P соответственно середины сторон BC и AC — треугольника ABC.
В треугольник TPC вписана окружность , длина радиуса которой равно 4 см.
Вычислите периметр треугольника ABC, если известно , что площать треугольника TPC равна 24 см в квадрате.
Видео:Взаимосвязь полупериметра, площади треугольника с радиусом вписанной в него окружности.Скачать

В прямоугольный треугольник вписана окружность?
В прямоугольный треугольник вписана окружность.
Найдите диаметр окружности, если сумма катетов равна
18 см, а гипотенуза треугольника равна
Видео:Треугольник и окружность #shortsСкачать

В прямоугольный треугольник вписана окружность?
В прямоугольный треугольник вписана окружность.
Найдите диаметр окружности, если сумма катетов равна 27 см, а гипотенуза треугольника равна 23 см.
На этой странице сайта размещен вопрос Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
Дано : Цилиндр ; R = 4 см h = 7 см Найти Р. Решение : Осевое сечение цилиндра — прямоугольник, у которого одна сторона это высота цилиндра h = 7 см, а вторая сторона это диаметр основания D = 2R = 2· 4см = 8 см Периметр прямоугольника P = 2(D + h) P..
Они имеют общую вершину.
АС и ВД — это диагонали Если АВ = СД, значит ВС = ДА. Тогда АС = ВД(по теореме про равность диагоналей).
Решение на фото….
Гипотенуза AB будет равна по выше иссказаным данным 9 см.
∠ABF = 180° (развернутый угол) ∠ABF = ∠ABD + ∠DBF = ∠ABС / 2 + ∠DBF ∠MBD = ∠MBF + ∠DBF = ∠KBF / 2 + ∠DBF ∠ABC = ∠KBF (вертикальные углы) ∠ABС / 2 = ∠KBF / 2 ∠MBD = ∠ABF = 180°.
По идее так. Радиус в в) ищется очень криво и мне кажется, что это неправильно. Г) я не осилил, ибо там тоже нужно прибегать к ф — лам, которые невозможно запомнить. Извини((.
Бери транспортир и мерий.
Если периметр квадрата равен 32 см, то его сторона в 4 раза меньше, 32 : 4 = 8 см. Площадь такого квадрата равна 8² = 64 см². Значит площадь параллелограмма S = a * h = 64 Т. К. высота равна 4, то основание будет 64 / 4 = 16 см.
Сторона треугольника a = 14, а высота h = 31 площадь треугольника найдем по формуле S = a×h / 2 подставим S = 14×31 / 2 = 434 / 2 = 217.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
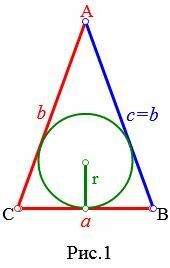 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
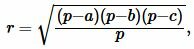 | (1) |
где полупериметр p вычисляется из формулы:
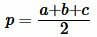 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac, ) | (3) |
| ( small p-a=frac-a ) ( small =frac, ) | (4) |
| ( small p-b=p-c=frac-b ) ( small =frac. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
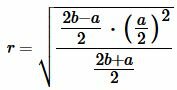 , , |
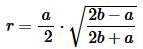 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
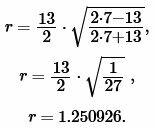 |
Ответ:
Видео:Вписанная окружностьСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
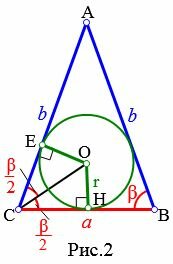 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:
| ( small frac=frac<large frac>=mathrmfrac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrmfrac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
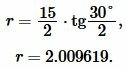 |
Ответ:
Видео:ПЛОЩАДЬ ТРЕУГОЛЬНИКА 3 (ВПИСАННАЯ ОКРУЖНОСТЬ)Скачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
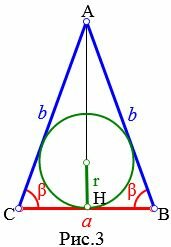 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac=frac<large frac>= cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac ) |
| ( small r=b cdot cos beta cdot mathrmfrac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
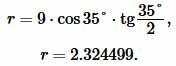 |
Ответ:
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
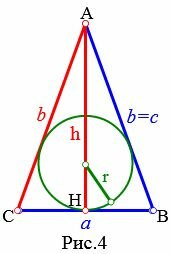 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
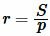 , , | (13) |
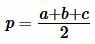 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( fracright)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
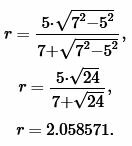 |
Ответ:
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
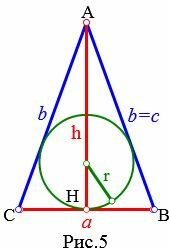 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >) |
| ( small r=large frac<a+ sqrt>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
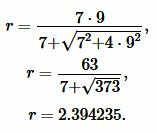 |
Ответ:
Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник?
Геометрия | 10 — 11 классы
Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник.
Я решил на листочке, прикрепил который.
Площадь треугольника равна 130 , а его периметр равен 52?
Площадь треугольника равна 130 , а его периметр равен 52.
Найдите радиус вписанной в треугольник окружности.
Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см?
Площадь треугольника ABC равна 96 см в квадрате, а его пириметр 18 см.
Вычислите диаметр окружности, вписаной в треугольник.
Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см?
Отрезок BT — медиана треугольника ABC, периметр которого равен 12 см.
Вычислите радиус окружности, вписанной в треугольник ABC, если известно , что площадь треугольника ABT равна 9 см2.
В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см ?
В прямоугольный треугольник вписана окружность радиус которой равен 3 см Вычислите периметр треугольника если его гипотенуза равно 20см .
Диаметр окружности описанной около правильного треугольника, равен 12корню из трех?
Диаметр окружности описанной около правильного треугольника, равен 12корню из трех.
Вычислите периметр этого треугольника.
Длина окружности, вписанной в правильный треугольник, равна 12П см?
Длина окружности, вписанной в правильный треугольник, равна 12П см.
Найдите периметр этого треугольника.
Радиус окружности, вписанной в правильный треугольник, равен корень из трех?
Радиус окружности, вписанной в правильный треугольник, равен корень из трех.
Найдите периметр и площадь треугольника.
Точки T и P соответственно середины сторон BC и AC — треугольника ABC?
Точки T и P соответственно середины сторон BC и AC — треугольника ABC.
В треугольник TPC вписана окружность , длина радиуса которой равно 4 см.
Вычислите периметр треугольника ABC, если известно , что площать треугольника TPC равна 24 см в квадрате.
В прямоугольный треугольник вписана окружность?
В прямоугольный треугольник вписана окружность.
Найдите диаметр окружности, если сумма катетов равна
18 см, а гипотенуза треугольника равна
В прямоугольный треугольник вписана окружность?
В прямоугольный треугольник вписана окружность.
Найдите диаметр окружности, если сумма катетов равна 27 см, а гипотенуза треугольника равна 23 см.
На этой странице сайта размещен вопрос Площадь треугольника abc равна 36 а периметр 18 вычислите диаметр окружности вписанной в треугольник? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.