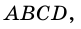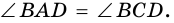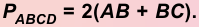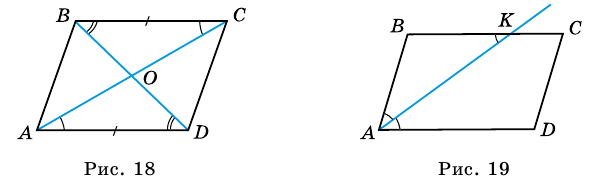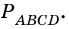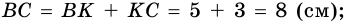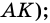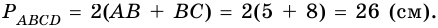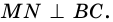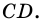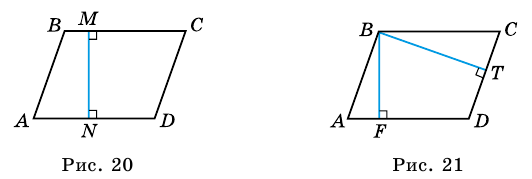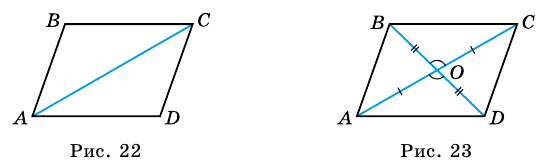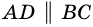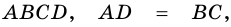Курс школьной геометрии » Четырехугольники

Параллелограмм является выпуклым четырехугольником доказательство

Обновлено
Параллелограмм, его свойства и признаки с примерами решения

Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

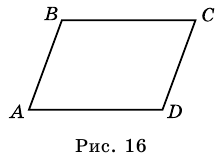
На рисунке 16 изображен параллелограмм Параллелограмм является выпуклым четырехугольником доказательство

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

Параллелограмм является выпуклым четырехугольником доказательство

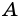
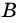
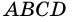
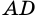
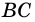
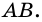
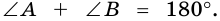
Действительно, углы Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствопараллелограмма Параллелограмм является выпуклым четырехугольником доказательство(рис. 16) являются внутренними односторонними углами для параллельных прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущей Параллелограмм является выпуклым четырехугольником доказательствоПоэтому Параллелограмм является выпуклым четырехугольником доказательствоАналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма.

2. Параллелограмм является выпуклым четырехугольником.

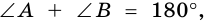
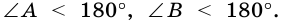
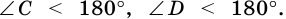
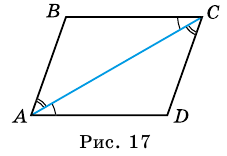
Так как Параллелограмм является выпуклым четырехугольником доказательството Параллелограмм является выпуклым четырехугольником доказательствоАналогично Параллелограмм является выпуклым четырехугольником доказательствоПоэтому параллелограмм — выпуклый четырехугольник.

3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Параллелограмм является выпуклым четырехугольником доказательство

Доказательство:

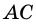
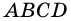
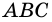
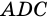
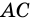
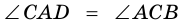
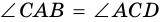
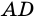
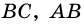
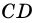
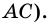
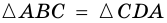
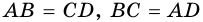
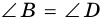
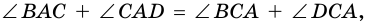
Диагональ Параллелограмм является выпуклым четырехугольником доказательстворазбивает параллелограмм Параллелограмм является выпуклым четырехугольником доказательствона два треугольника Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(рис. 17). Параллелограмм является выпуклым четырехугольником доказательство-их общая сторона, Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(как внутренние накрест лежащие углы для каждой из пар параллельных прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущей Параллелограмм является выпуклым четырехугольником доказательствоТогда Параллелограмм является выпуклым четырехугольником доказательство(по стороне и двум прилежащим углам). Откуда, Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(как соответственные элементы равных треугольников). Так как Параллелограмм является выпуклым четырехугольником доказательството Параллелограмм является выпуклым четырехугольником доказательство

4. Периметр параллелограмма Параллелограмм является выпуклым четырехугольником доказательство

5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

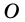
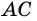
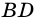
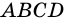
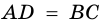
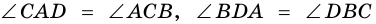
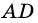
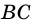
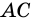
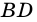
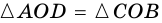
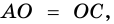
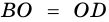
Пусть Параллелограмм является выпуклым четырехугольником доказательство— точка пересечения диагоналей Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствопараллелограмма Параллелограмм является выпуклым четырехугольником доказательство(рис. 18). Параллелограмм является выпуклым четырехугольником доказательство(как противолежащие стороны параллелограмма), Параллелограмм является выпуклым четырехугольником доказательство(как внутренние накрест лежащие углы для параллельных прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущих Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствосоответственно). Следовательно, Параллелограмм является выпуклым четырехугольником доказательство(по стороне и двум прилежащим углам). Тогда Параллелограмм является выпуклым четырехугольником доказательство Параллелограмм является выпуклым четырехугольником доказательство(как соответственные стороны равных треугольников).

Параллелограмм является выпуклым четырехугольником доказательство

Пример:

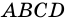
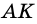
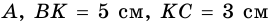
Дано: Параллелограмм является выпуклым четырехугольником доказательствопараллелограмм, Параллелограмм является выпуклым четырехугольником доказательство— биссектриса угла Параллелограмм является выпуклым четырехугольником доказательство(рис. 19). Найдите: Параллелограмм является выпуклым четырехугольником доказательство

Решение:

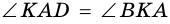
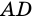
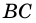
1) Параллелограмм является выпуклым четырехугольником доказательство

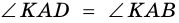
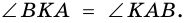
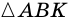
2) Параллелограмм является выпуклым четырехугольником доказательство(как внутренние накрест лежащие углы для параллельных прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущей Параллелограмм является выпуклым четырехугольником доказательство

3) Параллелограмм является выпуклым четырехугольником доказательство(по условию), тогда Параллелограмм является выпуклым четырехугольником доказательствоТогда Параллелограмм является выпуклым четырехугольником доказательство— равнобедренный (по признаку равнобедренного треугольника), Параллелограмм является выпуклым четырехугольником доказательство

4) Параллелограмм является выпуклым четырехугольником доказательство

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 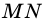Параллелограмм является выпуклым четырехугольником доказательство— высота параллелограмма, Параллелограмм является выпуклым четырехугольником доказательствоПараллелограмм является выпуклым четырехугольником доказательство

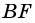
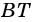
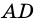
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство— высоты параллелограмма, проведенные соответственно к сторонам Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство

Параллелограмм является выпуклым четырехугольником доказательство

Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

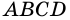
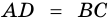
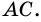
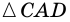
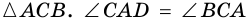
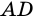
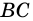
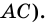
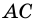
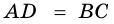
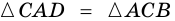
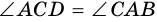
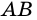
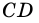
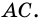
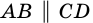
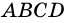
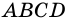
1) Пусть в четырехугольнике Параллелограмм является выпуклым четырехугольником доказательство Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(рис. 22). Проведем диагональ Параллелограмм является выпуклым четырехугольником доказательствоРассмотрим Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(как внутренние накрест лежащие при параллельных прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущей Параллелограмм является выпуклым четырехугольником доказательство Параллелограмм является выпуклым четырехугольником доказательство— общая сторона, Параллелограмм является выпуклым четырехугольником доказательство(по условию). Следовательно, Параллелограмм является выпуклым четырехугольником доказательство(по двум сторонам и углу между ними). Тогда Параллелограмм является выпуклым четырехугольником доказательство(как соответственные). Но это накрест лежащие углы при пересечении прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствосекущей Параллелограмм является выпуклым четырехугольником доказательствоПоэтому Параллелограмм является выпуклым четырехугольником доказательство(по признаку параллельности прямых). Следовательно, в четырехугольнике Параллелограмм является выпуклым четырехугольником доказательствопротиволежащие стороны попарно параллельны. Поэтому Параллелограмм является выпуклым четырехугольником доказательство-параллелограмм.

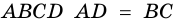
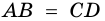
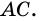
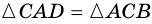
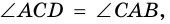
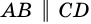
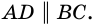
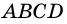
2) Пусть в четырехугольнике Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(рис. 22). Проведем диагональ Параллелограмм является выпуклым четырехугольником доказательствоТогда Параллелограмм является выпуклым четырехугольником доказательство(по трем сторонам). Поэтому Параллелограмм является выпуклым четырехугольником доказательствои следовательно, Параллелограмм является выпуклым четырехугольником доказательство(по признаку параллельности прямых). Аналогично доказываем, что Параллелограмм является выпуклым четырехугольником доказательствоСледовательно, Параллелограмм является выпуклым четырехугольником доказательство— параллелограмм.

Параллелограмм является выпуклым четырехугольником доказательство

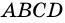
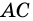
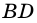
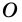
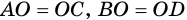
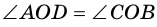
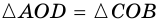
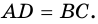
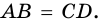
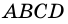
3) Пусть в четырехугольнике Параллелограмм является выпуклым четырехугольником доказательстводиагонали Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствопересекаются в точке Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство(рис. 23). Параллелограмм является выпуклым четырехугольником доказательство(как вертикальные). Поэтому Параллелограмм является выпуклым четырехугольником доказательство(по двум сторонам и углу между ними). Отсюда Параллелограмм является выпуклым четырехугольником доказательствоАналогично доказываем, что Параллелограмм является выпуклым четырехугольником доказательствоПринимая во внимание п. 2) этой теоремы, приходим к выводу, что Параллелограмм является выпуклым четырехугольником доказательство— параллелограмм.

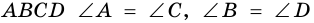
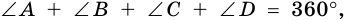
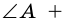
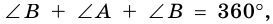
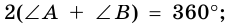
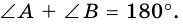
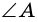
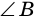
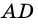
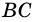
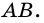
4) Пусть в параллелограмме Параллелограмм является выпуклым четырехугольником доказательство(рис. 16). Так как Параллелограмм является выпуклым четырехугольником доказательството Параллелограмм является выпуклым четырехугольником доказательство Параллелограмм является выпуклым четырехугольником доказательствот. е. Параллелограмм является выпуклым четырехугольником доказательствооткуда Параллелограмм является выпуклым четырехугольником доказательствоНо Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство— внутренние накрест лежащие углы для прямых Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательствои секущей Параллелограмм является выпуклым четырехугольником доказательствоПоэтому Параллелограмм является выпуклым четырехугольником доказательство

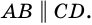
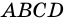
по признаку параллельности прямых). Аналогично доказываем, что Параллелограмм является выпуклым четырехугольником доказательствоСледовательно, Параллелограмм является выпуклым четырехугольником доказательство— параллелограмм.

Пример:

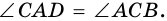
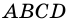
В четырехугольнике Параллелограмм является выпуклым четырехугольником доказательствоПараллелограмм является выпуклым четырехугольником доказательствоДокажите, что Параллелограмм является выпуклым четырехугольником доказательство— параллелограмм.

Доказательство:

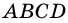
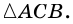
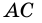
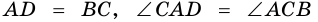
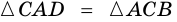
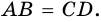
Пусть Параллелограмм является выпуклым четырехугольником доказательство— данный четырехугольник (рис. 22). Рассмотрим Параллелограмм является выпуклым четырехугольником доказательствои Параллелограмм является выпуклым четырехугольником доказательство Параллелограмм является выпуклым четырехугольником доказательство— их общая сторона, Параллелограмм является выпуклым четырехугольником доказательство(по условию). Тогда, Параллелограмм является выпуклым четырехугольником доказательство(по двум сторонам и углу между ними). Следовательно, Параллелограмм является выпуклым четырехугольником доказательствоНо тогда в четырехугольнике Параллелограмм является выпуклым четырехугольником доказательствопротиволежащие стороны попарно равны, поэтому он является параллелограммом.

О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

Термин «диагональ» — греческого происхождения; «диа» означает «через», а «гониос» — «угол», что можно понимать как отрезок, соединяющий вершины углов.

Следует отметить, что Евклид, как и большинство математиков того времени, для названия отрезка, соединяющего противолежащие вершины четырехугольника, в частности прямоугольника, употреблял другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои рассуждения основывали на вписанных в окружность прямоугольниках. В Средние века для названия упомянутого отрезка использовали оба термина. Лишь в XVIII в. термин «диагональ» стал общепринятым.

Рекомендую подробно изучить предметы:
  • Геометрия
  • Аналитическая геометрия
  • Начертательная геометрия
Ещё лекции с примерами решения и объяснением:
  • Площадь параллелограмма
  • Прямоугольник и его свойства
  • Ромб и его свойства, определение и примеры
  • Квадрат и его свойства
  • Свойство точек биссектрисы угла
  • Свойство катета прямоугольного треугольника, лежащего против угла в 30°
  • Четырехугольник и его элементы
  • Четырехугольники и окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание
  1. Четырехугольники
  2. теория по математике 📈 планиметрия
  3. Выпуклый четырехугольник
  4. Виды и свойства выпуклых четырехугольников
  5. Прямоугольник
  6. Квадрат
  7. Параллелограмм
  8. Трапеция
  9. Виды трапеций
  10. Средняя линия трапеции
  11. Всё о параллелограммах
  12. Определение параллелограмма
  13. Свойства параллелограмма
  14. Признаки параллелограмма
  15. Теоремы параллелограмма
  16. Параллелограммом является выпуклый четырехугольник
  17. Противоположные стороны и углы попарно равны
  18. Точка пересечения диагоналей разделяет их пополам
  19. Углы параллелограмма
  20. Свойства диагоналей параллелограмма
  21. Как вычислить площадь параллелограмма?
  22. Как вписать параллелограмм в окружность?
  23. Как вписать окружность в параллелограмм?
  24. Как начертить параллелограмм?
  25. Алгоритм построения квадрата
  26. Построение ромба
  27. Как построить прямоугольник
  28. Трапеция — это параллелограмм?
  29. Средняя линия параллелограмма
  30. Параллелограмм, у которого все стороны равны
  31. Ось симметрии параллелограмма
  32. 🔥 Видео

Видео:Геометрия 8 класс. Параллелограмм, свойства параллелограммаСкачать

Геометрия 8 класс. Параллелограмм, свойства параллелограмма

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Выпуклый четырехугольник

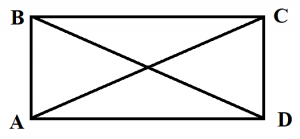
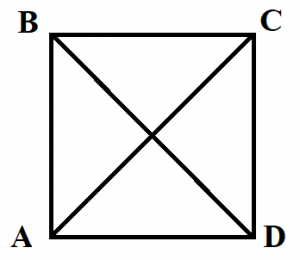
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Параллелограмм является выпуклым четырехугольником доказательствоОпределение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.Параллелограмм является выпуклым четырехугольником доказательство

Видео:№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

Параллелограмм является выпуклым четырехугольником доказательствоНа рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь Параллелограмм является выпуклым четырехугольником доказательство

  1. Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
  2. Диагонали прямоугольника равны (АС=ВD).
  3. Диагонали пересекаются и точкой пересечения делятся пополам.
  4. Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
  5. Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:

S=ab, где a и b соседние стороны прямоугольника.

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

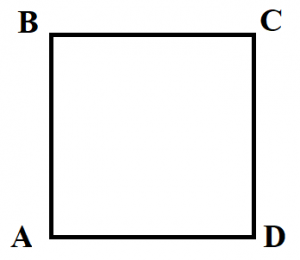
Параллелограмм является выпуклым четырехугольником доказательствоСвойства квадрата

  1. Диагонали квадрата равны (BD=AC).
  2. Диагонали квадрата пересекаются под углом 90 градусов.
  3. Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
  4. Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
  5. Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.

Параллелограмм является выпуклым четырехугольником доказательство

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Параллелограмм является выпуклым четырехугольником доказательство

Ромб – это параллелограмм, у которого все стороны равны.

Параллелограмм является выпуклым четырехугольником доказательство

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Параллелограмм является выпуклым четырехугольником доказательство

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

Параллелограмм является выпуклым четырехугольником доказательство

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Параллелограмм является выпуклым четырехугольником доказательство

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Параллелограмм является выпуклым четырехугольником доказательство

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).

Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .

Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Параллелограмм является выпуклым четырехугольником доказательство

Для нахождения площади трапеции в справочном материале есть формула

S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Параллелограмм является выпуклым четырехугольником доказательство

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Параллелограмм является выпуклым четырехугольником доказательство

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8= d 1 × 16 × 2 5 . . 2 . .

В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .

Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

Параллелограмм является выпуклым четырехугольником доказательство

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объектыяблонитеплицасарайжилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объектыяблонитеплицасарайжилой дом
Цифры3517

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Параллелограмм является выпуклым четырехугольником доказательство

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Параллелограмм является выпуклым четырехугольником доказательство

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Параллелограмм является выпуклым четырехугольником доказательство

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазинаРасход краскиМасса краски в одной банкеСтоимость одной банки краскиСтоимость доставки заказа
10,25 кг/кв.м6 кг3000 руб.500 руб.
20,4 кг/кв.м5 кг1900 руб.800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия

Всё о параллелограммах

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,

Определение параллелограмма

С этой фигурой знакомы все, освоившие курс школьной программы. Впервые с понятием «параллелограмм» встречаются в 8 классе на уроках геометрии.

Параллелограмм — геометрическая фигура, являющаяся разновидностью четырехугольника. Противоположные стороны параллельны.

Стоит отметить, что всем известные фигуры, такие как квадрат, ромб, прямоугольник, являются параллелограммами. Исходя из этого, им можно дать следующие определения:

  • Квадрат — параллелограмм с равными сторонами, пересекающимися под углом 90 градусов.
  • Ромб — параллелограмм с равными между собой сторонами, не пересекающимися под углом 90 градусов.
  • Прямоугольник — параллелограмм с неравными между собой сторонами, но пересекающимися под прямым углом.

Видео:Доказательство первого признака параллелограммаСкачать

Доказательство первого признака параллелограмма

Свойства параллелограмма

Для того чтобы определить параллелограмм, нужно обладать знанием о его свойствах. Рассмотрим их на примере четырехугольника MNPK.

Параллелограмм является выпуклым четырехугольником доказательство

  • Длина противоположных сторон фигуры одинакова.
  • Противоположные стороны параллельны.
  • Углы, являющиеся противоположными, равны.
  • Сумма всех четырех углов составляет 360 градусов.

∠NMK+∠NPK +∠MNP+∠MKP = 360°

  • Сумма двух соседних углов равна 180 градусов.
  • Диагонали разделяют параллелограмм на два треугольника, равные между собой.
  • При пересечении диагоналей образуется точка пересечения, представляющая собой центр симметрии.
  • Диагонали пересекаются и точка их пересечения разделяет каждую диагональ пополам.
  • Биссектриса, проведенная из любого угла, отделает от четырехугольника равнобедренный треугольник.

Видео:№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать

№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащих

Признаки параллелограмма

Четырехугольник MNPK можно называть параллелограммом при выполнении минимум одного условия:

  1. Противоположные стороны равны парами: MK=NP, MN=PK.
  2. Противоположные углы равны парами: ∠NMK=∠NPK, ∠MNP=∠MKP.
  3. Диагонали пересекаются, и точка их пересечения разделяет каждую диагональ пополам.
  4. Противоположные стороны равны и параллельны между собой: MK=NP, MN|PK.
  5. Сумма квадратов двух диагоналей равняется сумме квадратов четырех его сторон: MP²+NK²=MN²+NP²+PK²+MK².

Видео:№408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимноСкачать

№408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно

Теоремы параллелограмма

Все существующие теоремы доказывают свойства параллелограмма и исходят из определения о том, что это четырехугольник с противоположно расположенными параллельными сторонами.

Основные теоремы доказывают, что:

  • параллелограммом является выпуклый четырехугольник;
  • противоположные стороны попарно равны;
  • углы, являющиеся противоположными, попарно равны;
  • точка пересечения диагоналей разделает их пополам.

Параллелограммом является выпуклый четырехугольник

Многоугольник признается выпуклым при условии отсутствия продления до прямой хотя бы одной из сторон, а все оставшиеся стороны будут располагаться по одну сторону от этой прямой.

Пусть дан параллелограмм MNPK, сторона MN противоположна PK, а MK противоположна NP. Следовательно, исходя из определения, следует вывод о том, что MN || PK, а MK || NP.

Параллельные отрезки общих точек соприкосновения не имеют. Следовательно, PK находится со стороной MN по одну сторону. Отрезок NP соединяет точку N отрезка MN с точкой P отрезка PK. Противоположный отрезок MK соединяет оставшиеся две точки отрезков, что дает право утверждать о нахождении отрезков NP и MK по одну сторону от прямой MN. Исходя из всего вышесказанного, можно сделать вывод о том, что три стороны PK, NP и MK располагаются по одну сторону от отрезка MN.

Аналогичный алгоритм доказательства предположения о нахождении трех других сторон по одну сторону относительно остальных.

Противоположные стороны и углы попарно равны

Имеется четырехугольник MNPK, у которого MK=NP, MN=PK, ∠NMK=∠NPK, ∠MNP=∠MKP.

Параллелограмм — это, как мы знаем, четырехугольник. Следовательно, имеет 2 диагонали. Зная о том, что это выпуклая фигура, делаем вывод о делении фигуры на два треугольника. В нашем случае образовались треугольники MNP и MKP.

У треугольников имеется общее — сторона MP. ∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.

Следовательно, ΔMNP=ΔMKP, так как одна общая сторона и два равных смежных угла. Отсюда NP=MK, MN=PK.

∠NPM=∠PMK и ∠NMP=∠MPK

Из равенств следует, что ∠NMK=∠NPK.

Таким образом, теорема о равенстве противоположных углов и сторон доказана.

Точка пересечения диагоналей разделяет их пополам

Зная, что параллелограмм представляет собой выпуклый четырёхугольник, можно сказать о наличии двух пересекающихся диагоналей.

Есть четырехугольник MNPK с диагоналями NK и PM, пересекающимися в точке O. Возьмем два полученных треугольника MNO и PKO.

Параллелограмм является выпуклым четырехугольником доказательство

Из свойства противоположно лежащих сторон параллелограмма следует равенство MN=PK. Угол MNO и угол OKP — накрест лежащие, следовательно, они равны. Аналогично, два других угла — NMO и OPK — являются равными. Делаем вывод о равенстве треугольников MNO и PKO по стороне и двум углам.

Из рисунка видно, что углы MON и KOP вертикальные, а значит, они равны.

Зная о равенстве образовавшихся треугольников, можно утверждать и о равенстве всех соответствующих элементов. Сторона MO равна стороне PO, как и сторона NO=OK. Каждая из пар вместе представляет собой диагональ параллелограмма.

Таким образом, теорема о делении диагоналей пополам доказана.

Видео:8 класс, 4 урок, ПараллелограммСкачать

8 класс, 4 урок, Параллелограмм

Углы параллелограмма

Для углов действует правило, согласно которому смежные углы в сумме дают 180 градусов, а два противоположных равны друг другу. Основываясь на этих утверждениях, значения остальных углов находятся по формуле:

Видео:8 класс, 5 урок, Признаки параллелограммаСкачать

8 класс, 5 урок, Признаки параллелограмма

Свойства диагоналей параллелограмма

  1. Точка пересечения диагоналей разделяет их пополам.
  2. Любая диагональ разделяет фигуру на два треугольника, равные друг другу.
  3. Сумма квадратов его диагоналей равняется сумме квадратов всех его сторон.
  4. Площадь фигуры находится путем умножения длины диагоналей на синус угла, расположенного между ними, разделённый на 1/2.

Видео:Задание 25 Доказать, что четырёхугольник параллелограмм Определение параллелограммаСкачать

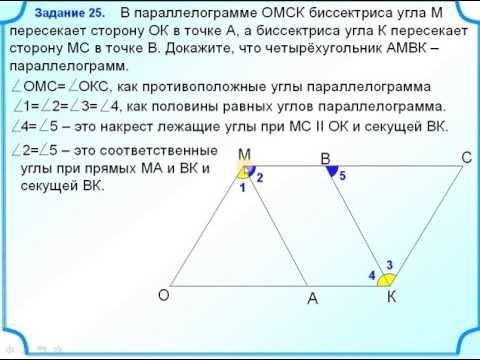
Задание 25 Доказать, что четырёхугольник параллелограмм Определение параллелограмма

Как вычислить площадь параллелограмма?

Существует несколько вариантов нахождения площади:

  1. По основанию и высоте: S=a*h.
  2. Зная значение двух смежных сторон и угла между ними: S=a*b*sin(α)°.
  3. По длине диагоналей и углу между ними: S=1/2*d1*d2*sin α.

Разберем подробнее последнюю формулу площади на примере. Дан параллелограмм с диагоналями АС и BD. Точка пересечения — О. Угол пересечения диагоналей в точке O = 60°. Отрезки AO=6 см и OD=5 см Площадь находится по формуле:

Зная свойство деления диагоналей точкой пересечения пополам, получаем:

AC=AO*2=12 см и DB=OD*2=10 см

Подставляем полученные значения в формулу:

S=1/2 * 12*10*1/2√3=51,962 см 2

Видео:№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

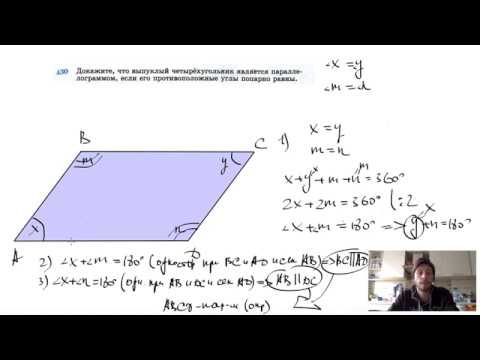
№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположные

Как вписать параллелограмм в окружность?

Вписанный параллелограмм — это когда фигура находится внутри окружности.

Не каждый параллелограмм можно поместить внутрь окружности. Эту манипуляцию можно проделать с той фигурой, у которой два противоположных угла в сумме составляют 180 градусов.

Из этого можно прийти к выводу, что у вписанного в окружность параллелограмма все четыре угла равны 90°. Параллелограмм бывает трех видов: квадрат, ромб, прямоугольник. Следовательно вписать в окружность можно прямоугольник, квадрат.

  1. Начертить окружность.
  2. Найти ее центр, обозначить буквой O.
  3. Выбрать любую точку на окружности и назвать ее точкой A.
  4. Если вписываем квадрат, то нужно построить два диаметра с углом между ними в 90 градусов. Точки пересечения диагоналей с окружностью соединить прямыми линиями.
  5. Для прямоугольника нужно иметь значения угла между диагоналями или размеры сторон. Зная размеры сторон по теореме Пифагора, высчитываем угол между диагоналями. Проведя один диаметр, обозначить точки пересечения с окружностью. От точки O (центр окружности и середина диагонали) отмерить угол между диагоналями. Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.

Видео:Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равныСкачать

Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равны

Как вписать окружность в параллелограмм?

В окружность можно вписать параллелограмм при условии равнозначных сумм противолежащих сторон. Из трех вариантов параллелограмма сумма противоположных сторон одинакова только у ромба. Следовательно, если в параллелограмм вписана окружность, то этот параллелограмм является ромбом.

  1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
  2. Провести горизонтальную линию, равную длине стороны.
  3. Транспортиром отмерить известный угол и провести луч.
  4. На луче отмерить тот же самый размер стороны.
  5. Оставшиеся две стороны нарисовать параллельно имеющимся.
  6. Согласно свойству ромба и вписанной окружности, проводим две биссектрисы из смежных углов (они же диагонали в ромбе).
  7. Пересечение биссектрис отметить точкой О.
  8. Точка О будет центром окружности.
  9. Вписанная окружность должна касаться всех сторон параллелограмма. Следовательно, стороны ромба будут касательными к окружности.
  10. Касательные перпендикулярны радиусу, который проходит к точке касания. Таким образом, из центра окружности (точки О) надо опустить перпендикуляр к любой стороне ромба.
  11. Иголку циркуля поставить в точку О, а ножку — на точку касания перпендикуляра со стороной ромба.
  12. Начертить окружность.
  13. Правильно начерченная фигура будет соприкасаться со всеми сторонами ромба.

Видео:ПАРАЛЛЕЛОГРАММ и его свойства. §2 геометрия 8 классСкачать

ПАРАЛЛЕЛОГРАММ и его свойства. §2 геометрия 8 класс

Как начертить параллелограмм?

Рассмотрим схему построения каждого вида по отдельности.

Алгоритм построения квадрата

  1. Узнать размер одной стороны. Этого достаточно, так как все стороны в квадрате равны.
  2. Один из признаков квадрата — все углы равны 90 градусов.
  3. Чертим прямую, равную длине одной стороны.
  4. С каждой стороны проводим перпендикулярную линию.
  5. На перпендикулярах отмечаем нужную длину и ставим точку.
  6. Соединяем две точки, построенные на перпендикулярных прямых.

Построение ромба

  1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
  2. Провести горизонтальную линию, равную длине стороны.
  3. Транспортиром отмерить известный угол и провести луч.
  4. На луче отмерить тот же самый размер стороны.
  5. Оставшиеся две стороны нарисовать параллельно имеющимся.

Как построить прямоугольник

  1. Нужно знать значения длины и ширины.
  2. Начертить прямую, равную длине.
  3. Провести два перпендикуляра с обеих сторон отрезка.
  4. Отметить на перпендикулярных линиях отрезок равный ширине прямоугольника.
  5. Соединить полученные два отрезка.
  6. При правильном построении полученная линия должны быть перпендикулярна длине (первой начерченной линии).

Видео:№ 378 - Геометрия 7-9 класс АтанасянСкачать

№ 378 - Геометрия 7-9 класс Атанасян

Трапеция — это параллелограмм?

Обе фигуры являются четырехугольниками с двумя противоположными сторонами, которые равны. Трапеция по определению имеет 2 непараллельные стороны. В параллелограмме все 4 стороны попарно параллельны.

Таким образом, трапеция не является параллелограммом.

Видео:Признак параллелограмма (если в четырехугольнике две стороны равны и параллельны, тоСкачать

Признак параллелограмма (если в четырехугольнике две стороны равны и параллельны, то

Средняя линия параллелограмма

Под этим термином понимается отрезок, соединяющий середины противоположных сторон параллелограмма.

Средняя линия всегда равна параллельной ей стороне

Свойства средней линии в параллелограмме:

  • точка пересечения диагоналей является точкой пересечения средних линий;
  • точка пересечения делит средние линии пополам;
  • точка пересечения выступает центром симметрии параллелограмма.

Видео:Признаки параллелограмма. 8 класс.Скачать

Признаки параллелограмма. 8 класс.

Параллелограмм, у которого все стороны равны

Все четыре стороны имеют равное значение в двух разновидностях фигуры — ромбе и квадрате.

Видео:Параллелограмм. 8 класс.Скачать

Параллелограмм. 8 класс.

Ось симметрии параллелограмма

Под осью симметрии понимается прямая, разделяющая фигуру на две зеркально равные фигуры.

В прямоугольнике осью симметрии являются прямые, которые проходят через середину противоположной стороны.

В ромбе оси симметрии представляют собой его 2 диагонали.

Квадрат, объединяя в себе две предыдущие фигуры, имеет 4 оси симметрии: 2 диагонали и 2 средние линии.

🔥 Видео

Геометрия 8. Урок 2 - Параллелограмм. Свойства и признаки.Скачать

Геометрия 8. Урок 2 - Параллелограмм. Свойства и признаки.

Признаки параллелограмма Доказательство признаков параллелограммаСкачать

Признаки параллелограмма Доказательство признаков параллелограмма

Первый признак параллелограмма (доказательство).Скачать

Первый признак параллелограмма (доказательство).
Поделиться или сохранить к себе: