Как найти дельта вектора (4 видео) | Курс школьной геометрии

Дельта-функция Дирака и ее свойства

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

При рассмотрении преобразования Фурье мы говорили, что условием существования преобразования Фурье является абсолютная интегрируемость исходного сигнала :

К счастью, в первой половине XX века в теоретической физике произошли большие перемены. Появилась теории относительности и квантовой механики, которые потребовали переосмыслить понятие функции в целом. В результате была разработана теория обобщенных функций, которые расширили область применения методов математического анализа, устранили некоторые неопределенности в физике, а также расширили применимость методов спектрального анализа на функции, для которых условие абсолютной интегрируемости не выполняется. Кроме того, использование аппарата обобщенных функций позволило сформулировать и обосновать переход от аналоговых непрерывных сигналов и систем к дискретным и цифровым.

Математическую теорию обобщенных функций можно найти в литературе [1, 2, 3, 4]. Нас будет особенно интересовать дельта-функция Дирака, свойства которой позволяют распространить преобразование Фурье на случай неинтегрируемых сигналов, а также находят широкое применение в теории обработки сигналов.

Содержание

Путь и перемещение
Перемещение
Примеры задач на путь и перемещение
Дельта-вектор в сверточных алгебрах
📹 Видео

Видео:Дельта альфа альфа штрих | МФТИСкачать

Путь и перемещение

При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.

Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.

При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:

где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.

Его можно вычислить, если известен модуль скорости ($v=v_x$):

[Delta s=vt left(2right),]

где $t$ — время движения тела.

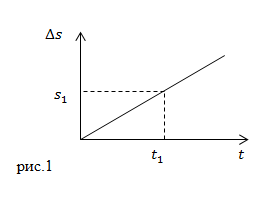
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.

Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку $_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.

Путь не бывает меньше нуля и не может уменьшаться при движении тела.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Перемещение

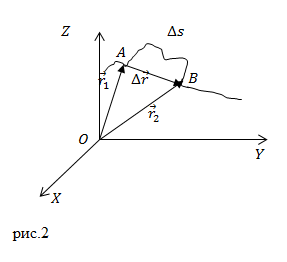
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:

[Delta overline=overlineleft(t+Delta tright)-overlineleft(tright)left(3right).]

Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.

Приращение радиус-вектора материальной точки — это перемещение ($Delta overline$).

В декартовой системе координат радиус-вектор точки представляют в виде:

где $overline$, $overline$,$ overline$ — единичные орты осей X,Y,Z. Тогда $Delta overline$ равен:

[Delta overline=left[xleft(t+Delta tright)-xleft(tright)right]overline+left[yleft(t+?tright)-yleft(tright)right]overline+left[zleft(t+?tright)-zleft(tright)right]overlineleft(5right).]

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:

[left|Delta overlineright|=Delta s left(6right).]

Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overlineright|$ или просто $Delta r$ (без указания стрелки).

Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:

Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Примеры задач на путь и перемещение

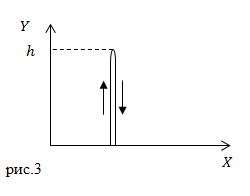
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?

Решение: Сделаем рисунок.

В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:

Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:

Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$

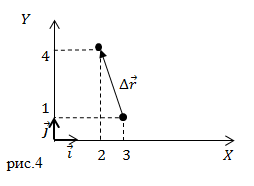
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?

Решение: Сделаем рисунок.

Радиус — вектор начальной точки запишем как:

Радиус — вектор конечной точки имеет вид:

Вектор перемещения представим как:

Из формулы видим, что:

[Delta r_x=-1;;Delta r_y=3. ]

Ответ: $Delta r_x=-1;;Delta r_y=3 $

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Дельта-вектор в сверточных алгебрах

Омский государственный университет путей сообщения (ОмГУПС(ОмИИТ))

ДЕЛЬТА-ВЕКТОР В СВЕРТОЧНЫХ АЛГЕБРАХ

В математике и физике уже долгое время используется понятие дельта-функции. Это очень удобный математический объект, позволяющий эффективно решать большой круг научных задач. К сожалению, при работе с дельта-функцией возникают и серьезные проблемы. Например, нельзя перемножать дельта-функции. Дифференцирование дельта-функций также приводит к весьма неоднозначным результатам. Иногда применение дельта-функции является причиной появления нескольких взаимоисключающих решений для одной задачи.

В данной статье дельта-функция рассматривается немного под другим углом — это ни есть раз и навсегда заданная функция. Существуют пространства векторов, среди которых возможно найти вектор, обладающий всеми свойствами дельта-функции по отношению к векторам своего пространства.

Предположим, что задано пространство Гильберта . Пусть , и — произвольные вектора пространства , являющиеся действительными функциями переменной , принадлежащей некому множеству .

где . При этом, если — любой вектор пространства , то и , при любом .

Следовательно, на множестве задано также и скалярное произведение двух векторов [1]:

. (1)

Определим на базе скалярного произведения (1) двух произвольных векторов пространства Гильберта понятие свертки:

Определение 1: сверткой двух произвольных векторов пространства Гильберта является третий вектор этого же пространства, получаемый из следующего соотношения:

. (2)

Докажем для свертки свойство коммутативности.

Лемма 1. В отношении свертки двух произвольных векторов пространства Гильберта истинны следующие соотношения:

С учетом подстановки и имеем:

Что и требовалось доказать.

На базе введенного понятия свертки (2) определяем дельта-вектор пространства Гильберта.

Определение 2: дельта-вектором пространства Гильберта , на котором определена свертка, называется такой вектор , в отношении которого выполняется условие:

, (3)

где – любой вектор пространства .

Теорема 1. Если в пространстве Гильберта, в котором определен ортогональный базис и свертка, существует дельта-вектор, то этот вектор единственный и может быть вычислен по следующей формуле:

Доказательство. Пусть — произвольный вектор пространства Гильберта. Имеем по определению дельта-вектора (3):

. (4)

Разложим вектора и по базису :

где и — коэффициенты разложения. С учетом равенства Парсеваля формула (4) преобразуется следующим образом:

Разложим по базису и получим следующее:

, (5)

так как — любой вектор, то коэффициенты — могут быть любыми, кроме того они независимы. Следовательно, равенство (5) может быть истинно только при условии

И так, любой вектор раскладывается единственным образом в любом базисе:

а вектор соответственно:

Что и требовалось доказать.

Докажем некоторые свойства дельта-вектора пространства Гильберта.

Лемма 2: квадрат нормы (или энергия) дельта-вектора пространства Гильберта всегда равен .

Вводим подстановку: , :

используем свойство коммутативности свертки:

Что и требовалось доказать.

Рассмотрим другое важное свойство дельта-вектора – четность (симметричность). Для доказательства этого сначала докажем такое интересное свойство свертки:

Лемма 4: для любого произвольного и истинно следующее соотношение:

Для доказательства в формулу:

введем подстановку: ,

Исходя из определения дельта-вектора получаем:

Что и требовалось доказать.

Теперь можно доказать четность дельта-вектора.

Лемма 5: для любого произвольного истинно соотношение:

Как следствие Леммы 4, истинны утверждения, что

Но из определения скалярного произведения:

Что и требовалось доказать.

Введем в рассматриваемое пространство понятие единичного вектора.

Определение 3: Единичным вектором будем считать такой вектор, для которого справедливо соотношение:

Очевидно, что в рассматриваемом пространстве действительных функций, единичный вектор является действительной функцией . Для дальнейшего описания свойств дельта-вектора введем понятие площади вектора.

Определение 4: площадью вектора пространства Гильберта, если в нем определен единичный вектор является действительное число , определяемое следующим соотношением:

. (6)

Докажем следующее свойство дельта-векотра.

Лемма 6. Площадь дельта-вектора всегда равна 1.

Найдем площадь дельта-вектора в соответствии с формулой (6):

Что и требовалось доказать.

Теперь рассмотрим интерполяционные возможности дельта-вектора. Для этого предположим, что у нас имеется набор из «смещенных» по оси функций вида . Предположим, что функции образуют полный ортогональный базис. В этом случае, по этим функциям возможно разложить любой вектор пространства .

Теорема 2. Если в пространстве Гильберта возможно задать полный ортогональный базис размерности состоящий из функций вида , то любой вектор этого пространства может быть однозначно восстановлен по своим значениям в точках .

Так как, функции образуют полный ортогональный базис, то вектор возможно разложить по этому базису:

, (7)

где – размерность базиса рассматриваемого пространства; – интервал значений . Остается только найти коэффициенты разложения по данному базису:

Таким образом, формула (7) принимает вид:

. (8)

Это означает, что имея только отсчеты вектора в точках возможно полностью восстановить весь вектор. Что и требовалось доказать.

Приведем пример пространства, в котором существует дельта-вектор. Таким пространством является множество всех функций со спектром, ограниченным отрезком . Скалярным произведением векторов и этого пространства выберем следующее известное соотношение [2]:

Исходя из формулы (4) получим, что для дельта-вектора данного пространства справедливо соотношение:

где — любой вектор рассматриваемого пространства. Данное соотношение – это классическая свертка двух функций и . Сразу оговоримся, что классическая дельта-функция Дирака в данном случае дельта-вектором выступать не может, так как ее спектр не ограничен интервалом и, следовательно, она не является вектором нашего пространства. Необходимо искать дельта вектор среди функций с ограниченным спектром.

Как известно из теории [2], классическая свертка во временной области соответствует перемножению спектров функций в спектральной области. Подберем такую функцию , спектр которой в отношении спектра любой функции рассматриваемого пространства обладает свойством:

А таким спектром обладает функция:

. (9)

Известно, что смещенные по оси времени на интервалы функции вида (9) образуют полный ортогональный базис. Учитывая, что , а , формула (8) приобретает вид широко известной интерполяционной формулы Котельникова [3]:

где .

В заключении приведем основные результаты, полученные в данной работе.

1. Дельта-функция Дирака не является уникальным математическим объектом. Существуют пространства Гильберта, в которых имеется вектор, обладающий свойствами дельта-функции в отношении всех векторов своего пространства.

2. Площадь дельта-вектора равна 1.

3. Квадрат нормы (энергия) дельта-вектора равна значению этого вектора в точке 0.

4. Если в пространстве Гильберта, в котором определен ортогональный базис и свертка, существует дельта-вектор, то этот вектор единственный и может быть стандартно вычислен из любого базиса этого пространства.

5. Дельта-вектор обладает свойством симметрии.

6. В пространстве функций, ограниченных по Котельникову существует дельта-вектор, определяемый формулой:

1. Элементарное введение в абстрактную алгебру: М.:Мир, 1979.

2. Кудрявцев математического анализа (в двух томах): Учебник для студентов университетов и втузов. М.: Высш. школа, 1981.

3. Романюк цифровой обработки сигналов. М.:МФТИ, 2005.