Конспект свойство биссектрисы треугольника (6 видео)

Урок геометрии в 8 классе «Свойство биссектрисы угла»
план-конспект урока по геометрии (8 класс) на тему

Урок по теме «Свойство биссектрисы угла» составлен согласно технологий: системно-деятельностного подхода и «Мастерских».

Содержание

Скачать:
Предварительный просмотр:
Конспект урока на тему «Свойства биссектрисы угла треугольника»
Элементы треугольника. Биссектриса
Свойства биссектрисы
Некоторые формулы, связанные с биссектрисой треугольника
📹 Видео

Видео:Свойство биссектрисы треугольникаСкачать

Скачать:

Вложение	Размер
svoystvo_bissektrisy_ugla.rar	2.29 МБ

Видео:3 свойства биссектрисы #shortsСкачать

Предварительный просмотр:

06.04.2017 Урок геометрии в 8 «А» классе

Тема: » Свойство биссектрисы угла»

Тип урока : урок изучения и первичного закрепления новых знаний и способов деятельности (1 тип)

1.Рассмотреть теоремы о свойстве биссектрисы угла и её следствиях.

2. Учить применять данные теоремы и следствия при решении задач.

3. Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.

4. Продолжать развивать познавательную активность, умение формулировать свои выводы и доказывать их.

5. Воспитывать уверенность в себе, познавательный интерес.

Оборудование: компьютер, проектор, презентация, чертёжные инструменты, раздаточный материал (треугольные листы бумаги) .

I. Орг. момент: постановка темы и целей урока

( мотивация ). Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии.

Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения — никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

Мы опять возвращаемся к теме «Треугольники». Что мы знаем и умеем на данный момент? Мы знаем определение и виды треугольника, линии треугольника, некоторые свойства и признаки, умеем решать задачи, связанные с треугольниками. Как вы считаете, какую тему, связанную с линиями треугольника мы еще не изучили? Конечно, свойство биссектрисы угла. Поэтому, это и будет темой нашего урока. Как вы думаете, чему мы будем сегодня учиться? (учить теоремы о свойстве биссектрисы угла и ее следствия). Что нам для изучения новой темы необходимо повторить? (линии треугольника). Поэтому план урока сегодня такой: мы повторим пройденный материал, изучим новую тему, закрепим её, и в конце урока проверим уровень усвоения нового материала.

Ключевые слова: знаю, смогу

II. Повторение пройденного материала ( актуализация)

Для того чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал. Сначала: определение биссектрисы угла (с помощью планиметрического прибора)

— луч, исходящий из вершины угла и делящий его на два равных угла называется биссектрисой угла

Какие линии в треугольнике вам известны?

-К числу линий треугольника относятся:

— Перпендикуляр, проведенный из вершины треугольника к противоположной стороне, называется высотой треугольника;

— Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника;

— Биссектриса треугольника — отрезок биссектрисы угла, соединяющий вершину треугольника с точкой противоположной стороны.

• серединные перпендикуляры к сторонам треугольника

— Перпендикуляр, проведенный из вершины треугольника к середине противоположной стороны, называется серединным перпендикуляром;

(Повторение определений основных линий в треугольнике путём фронтальной беседы)

III. Работа по новой теме ( организация восприятия )

1. Работа с чертёжными инструментами на доске (4 ученика)

построение биссектрисы, медианы, высоты, серединного перпендикуляр в треугольнике.

2. Практическая работа с бумагой (работа в паре)

Каждый ряд получает задание (используя треугольный лист бумаги): построить сгибанием точку пересечения биссектрис.

I ряд: с помощью сгибов постройте биссектрисы в остроугольном треугольнике.

II ряд: с помощью сгибов постройте биссектрисы в тупоугольном треугольнике. III ряд: с помощью сгибов постройте биссектрисы в прямоугольном треугольнике.

Вывод: Биссектрисы углов треугольника пересекаются в одной точке.

С каждым треугольником связаны 4 совершенно особые точки. Эти точки называются замечательными точками. (Слайд 4)

3. Формулировка теоремы. (Слайд 5)

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. (Слайд 5)

4. Доказательство теоремы (Слайд 6)

5. Доказательство следствия из теоремы. (Слайд 7)

Биссектрисы треугольника пересекаются в одной точке.

IV. Закрепление изученного материала.

Решить №№ 676 (б). (Слайд 8 – условие, слайд 9- решение)

Дано: стороны угла А, равного 90°,

касаются окружности с центром О

и радиусом r, ОА = 14 дм.

Решение: 1) ( так как касательная перпендикулярна к радиусу, проведенному в точку касания, по определению касательной)

2). АО – биссектриса угла А (так как точка О равноудалена от сторон угла).

3). ∆АОР – прямоугольный. По теореме Пифагора ОР² +АР² =АО².

r ² + r ² = 14², 2r ² = 196, r ² =98, r = .

Дополнительно: № 678 (а) (самопроверка) (слайд 10)

Дано: ∆АВС, АА 1 и ВВ 1 биссектрисы углов А и В,

Решение: 1) СМ – биссектриса угла С, так как биссектрисы углов в треугольнике пересекаются в одной точке.

V. Домашнее задание: вопросы п.74; стр. 177 №№ 676 (а), 678 (б)- прокомментировать (слайд 11)

Вспомним ключевые слова урока: знаю и смогу.

Доказать теорему о биссектрисе угла

Доказать следствие из теоремы

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Конспект урока на тему «Свойства биссектрисы угла треугольника»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Тема урока: Свойства биссектрисы угла треугольника.

Цели урока: Рассмотрение теоремы о свойстве биссектрисы треугольника и её следствие; развитие познавательного интереса; воспитание уверенности в себе
Задачи урока: 1) Обучающая: Рассмотреть теорему о свойстве биссектрисы треугольника и её следствие; учить применять данную теорему и следствие при решении задач.

2) Развивающая: развивать познавательный интерес; формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.

3) Воспитывающая: воспитывать уверенность в себе.

1. Организационный момент.

Взаимное приветствие учителя и учащихся.

2. Объявить тему урока. Определить цели урока

3. Проверка домашнего задания.

Проверка на доске (пару работ лично)

4. Актуализация нового материала.

Для того чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал.

Какие линии в треугольнике вам известны?

-К числу линий треугольника относятся:

Устная фронтальная работа по обобщению теоретического материала.

Какие из следующих утверждений верны?

Биссектриса всегда проходит через середину стороны треугольника.
Любая биссектриса равнобедренного треугольника является его медианой.
Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

Сегодня мы изучим еще несколько свойств биссектрисы.

Биссектрисы треугольника пересекаются в одной точке инцентре фигуры.

Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

Доказательство теоремы. Тест 1, 2 усно

Упражнение для глаз

ü Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5. Египетский треугольник с соотношением сторон 3:4:5 применялся египтянами землемерами и архитекторами для построения прямых углов. Несмотря на возраст, это способ построения прямого угла активно используется строителями и теперь. (Слайд 4, 6).

ü Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. (Слайды 4, 7).

ü Треугольник Рёло — это геометрическая фигура, образованная пересечением трёх равных кругов одинакового радиуса с центрами в вершинах равностороннего треугольника. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с неточностью в 2%). (Слайды 4, 8).

ü Один из самых загадочных и интересных треугольников – “Бермудский треугольник”. Еще это место называют аномальной зоной. На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов — большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках никого и ничего не удалось обнаружить. Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение — это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь — 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский треугольник” не является географическим. (Слайды 4, 9).

ü Треугольник Пенроуза … Эта фигура –возможно, первый опубликованный в печати невозможный объект. Она появилась в 1958 году в журнале. в статье под заголовком «Удивительные фигуры, особый вид оптических иллюзий». Ее авторы, отец и сын Лайонелл и Роджер Пенроузы. Невозможный » треугольник, треугольник Пенроуза, увековечен в виде статуи в городе Перт (Австралия). Созданный усилиями художника Брайна МакКея и архитектора Ахмада Абаса, он был воздвигнут в парке Клайзебрук в 1999 году и теперь все проезжающие мимо могут видеть «невозможную» фигуру. (Слайды 4, 10).

№ 318 трое учащихся возле доски

Карточки для самостоятельного закрепления умений и навыков (для слабых учащихся)

Домашнее задание № 320, 321

Итог урока. Рефлексия

Что изучили сегодня? Что в изучаемом материале было легким? Что было непонятным?

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Видео:Свойства биссектрисы треугольникаСкачать

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

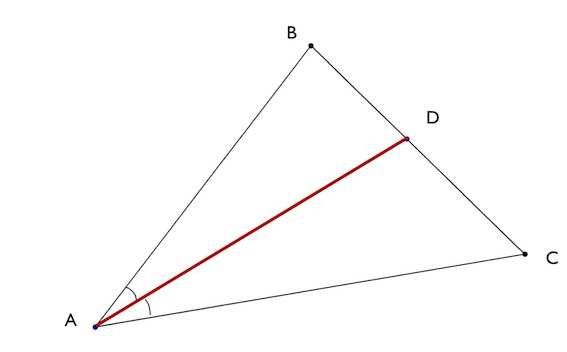
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Видео:Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1