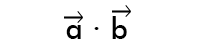Отражение вектора относительно плоскости

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Project, Reject, Reflect: проекции и отражения вектора. Space Engineers, KSP, From the DepthsСкачать

Линейный оператор

Линейное отображение линейного (векторного) пространства $ mathbb V_ $ в себя $$ mathcal A : mathbb V longmapsto mathbb V $$ называется линейным преобразованием $ mathbb V_ $ или линейным оператором 1) на $ mathbb V_ $.

Напомню свойство линейности: $$ mathcal A (X_1 +X_2)= mathcal A(X_1) + mathcal A(X_2),quad mathcal A (alpha_1 X_1)= alpha_1 mathcal A (X_1), $$ или, в эквивалентном виде: $$ mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) + alpha_2 mathcal A(X_2) $$ для $ forall subset mathbb V, forall subset mathbb R mbox mathbb C $ (здесь $ alpha_1,alpha_ 2 $ — константы из $ mathbb R_ $ если $ mathbb V_ $ вещественное пространство, и из $ mathbb C_ $, если оно комплексное).

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Примеры линейных операторов

Бóльшую часть примеров пункта ☞ ПРИМЕРЫ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ представляют именно линейные операторы. Укажу еще несколько, к которым буду часто обращаться.

Пример 1. В пространстве $ mathbb R^ $ рассмотрим следующие действия над вектором 2) $ (x_,y,z) $:

Все это — примеры линейных операторов. Но вот отображение сдвига $ (x,y,z) mapsto (x+1,y,z+2) $ оператором не является поскольку $$ <coloralpha > (x,y,z) = ( <coloralpha > x, <coloralpha > y, <coloralpha > z) mapsto ( <coloralpha > x+1, <coloralpha > y, <coloralpha > z+2) ne <coloralpha > (x+1,y,z+2) . $$

Пример 2. В пространстве $ mathbb R^ $ отображение ортогонального проецирования на плоскость $ x+y-7, z=0 $ будет линейным оператором (а вот на плоскость $ x+y-7, z=1 $ — не будет!). Вообще, в произвольном пространстве $ mathbb V_ $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ отображение, сопоставляющее вектору $ X_ $ его проекцию на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $, будет оператором.

Пример 3. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степеней $ le 3 $ отображение $ mathcal A_ $ действует по правилу

$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Это отображение будет оператором в $ mathbb P_3 $. Действительно, если $$ begin f_1(x)(x^2-2) equiv q_1(x)(x^4-x^3-x^2+x)+ r_1(x), , \ f_2(x)(x^2-2) equiv q_2(x)(x^4-x^3-x^2+x)+ r_2(x) , end $$ при $ subset mathbb R[x], deg r_1(x) le 3, deg r_2(x) le 3 $, то $$ (alpha_1 f_1(x)+alpha_2 f_2(x)) (x^2-2) equiv (alpha_1 q_1(x)+alpha_2 q_2(x))(x^4-x^3-x^2+x)+ (alpha_1 r_1(x)+alpha_2 r_2(x)) ; $$ очевидно, что $ deg (alpha_1 r_1(x)+alpha_2 r_2(x)) le 3 $. ♦

Пример 4. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице

$$ begin x & x_1 & x_2 & dots & x_n \ hline y & y_1 & y_2 &dots & y_n end qquad npu qquad < x_, dots, x_, y_,dots,y_ > subset mathbb C $$ будем считать узлы $ _^n $ фиксированными, а значения $ _^n $ — переменными. Эта таблица однозначно определяет интерполяционный полином $ f(x)=A_+A_1x+dots+A_x^ $ со свойством $ f(x_j)=y_j $ при $ j in $. При этом $ <A_>_^ subset mathbb C $. Будет ли получившееся отображение $$ (y_1,dots,y_n) mapsto (A_0,A_1,dots,A_) $$ оператором на $ mathbb C^n $? Покажем, что отображение $$ mathcal A(y_1,dots,y_n) = f(x) in mathbb C[x] $$ является линейным отображением. Действительно, решением задачи интерполяции для таблицы $$ begin x & x_1 & x_2 & dots & x_n \ hline y & alpha y_1 & alpha y_2 &dots & alpha y_n end qquad npu qquad forall alpha in mathbb C $$ является полином $ alpha f(x) $. Если же, вдобавок, решением задачи интерполяции для таблицы $$ begin x & x_1 & x_2 & dots & x_n \ hline y & z_1 & z_2 &dots & z_n end qquad npu qquad < z_,dots,z_ > subset mathbb C $$ является полином $ g(x)in mathbb C[x], deg g(x) le n-1 $, то решением задачи интерполяции для таблицы $$ begin x & x_1 & x_2 & dots & x_n \ hline y & y_1+z_1 & y_2+z_2 &dots & y_n+z_n end qquad $$ будет полином $ f(x)+g(x) $ и этот полином будет единственным решением среди полиномов степеней $ le n-1 $. Таким образом, линейность отображения $ mathcal A $ установлена. Далее, множество $ mathbb P_ $ полиномов из $ mathbb C[x] $ степеней $ le n-1 $ изоморфно пространству $ mathbb C^n $. Следовательно, «сложное» отображение $$ (y_1,dots,y_n) mapsto f(x)=A_+A_1x+dots+A_x^ mapsto (A_0,A_1,dots,A_) $$ является линейным отображением из $ mathbb C^n $ в $ mathbb C^n $, т.е. оператором на $ mathbb C^n $.

По аналогии с задачей алгебраической интерполяции, можно поставить и задачу тригонометрической интерполяции. Имеем здесь «точку входа» в теорию дискретного преобразования Фурье. ♦

В пространстве $ mathbb P_2 $ оператор действует следующим образом:

$$ mathcal A (x^2+x+1) =2,x+1, mathcal A (x^2-x-1) =2,x^2-1, mathcal A (x+1) =-x^2+x+1 . $$ Вычислить $ mathcal A (x^2) $ и $ mathcal A (x^2+1) $.

Пример 5. В пространстве полиномов степени не выше $ n_ $ с вещественными коэффициентами от $ m_ $ переменных $ x_1,x_2,dots,x_ $ отображение

$$ f(x_1,x_2,dots,x_m) mapsto frac +frac+ dots+ frac $$ яыляется линейным оператором. Этот оператор известен как оператор Лапласа и для него используется символьное обозначение $$ Delta = frac +frac+ dots+ frac , . $$

Пример 6. В линейном пространстве квадратных матриц порядка $ n_ $ с вещественными элементами рассмотрим коммутирующее отображение

$$ mathcal K (X) = AX-XA , $$ а также отображение Ляпунова $$ mathcal V (X) = A^X+XA $$ при произвольной фиксированной квадратной матрице $ A_ $ и $ ^ $ означающем транспонирование. Легко проверить, что оба отображения $ mathcal K $ и $ mathcal V $ являются операторами. ♦

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Основные определения

Все введенные для линейного отображения понятия переносятся на этот частный случай. Например, ядром оператора называется множество векторов, отображаемых оператором в нулевой вектор: $$mathcaler (mathcal A)= left ; $$ а образом оператора называется множество всех векторов из $ mathbb V_ $, для каждого из которых существует прообраз в том же пространстве: $$mathcalm (mathcal A)= left .$$

Теорема 1. Множества $ mathcaler (mathcal A) $ и $ mathcalm (mathcal A) $ являются подпространствами пространства $ mathbb V_ $.

Доказать, что для оператора в $ mathbb R^4 $

$$ mathcal A left(begin x_1 \ x_2 \ x_3 \ x_4 end right)= left(begin x_3 \ x_4 \ 0 \ 0 end right) $$ имеет место равенство $ mathcaler (mathcal A) = mathcalm (mathcal A) $.

Для оператора $ mathcal A_ $ его дефектом его называется размерность ядра, а его рангом — размерность образа: $$ operatorname(mathcal A )=dim (mathcaler (mathcal A )) , operatorname(mathcal A )= dim (mathcalm (mathcal A )) . $$ Оператор называется невырожденным если $ operatorname(mathcal A )=0 $.

Пример. В пространстве $ mathbb R^ $ оператор проецирования на плоскость:

$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right) $$ является вырожденным поскольку его ядро нетривиально: $ mathcaler (mathcal A)= $. ♦

Следующий результат является следствием теоремы $ 4 $ из ☞ ПУНКТА.

Теорема 2. Имеет место равенство:

$$ dim mathbb V=dim left( mathcaler (mathcal A) right) + dim left( mathcalm (mathcal A) right) = operatorname(mathcal A )+ operatorname(mathcal A ) .$$

Говорят, что операторы $ mathcal A $ и $ mathcal B $ коммутируют если $ mathcal A , mathcal B = mathcal B , mathcal A $.

Пример. В пространстве полиномов $ mathbb P_ $ рассмотрим дифференциальный оператор

$$mathcal A = xfractimes Box — 1times Box : mathcal A(p(x)) = x p'(x) — p(x) .$$ Этот оператор не коммутирует с обычным оператором дифференцирования $ displaystyle mathcal B= frac $: $$mathcal A (x^2)=x^2, quad mathcal B (mathcal A(x^2))=2,x, quad mathcal B (x^2)=2,x, quad mathcal A (mathcal B (x^2))=0 .$$ ♦

Оператор $ mathcal E $, отображающий произвольный вектор $ Xin mathbb V_ $ в себя : $ mathcal E(X)= X $, называется тождественным на $ mathbb V_ $. Оператор $ mathcal B $ называется (левым) обратным оператору $ mathcal A_ $, если $ mathcal Bmathcal A=mathcal E $. В этом случае оператор $ mathcal A_ $ называют обратимым и записывают: $ mathcal B=mathcal A^ $.

Не всякий оператор обратим.

Пример. В пространстве $ mathbb R^ $ для оператора проецирования на плоскость:

$$ mathcal A left(x, y, zright) longmapsto left(x, y, 0 right) $$ обратного не существует, т.к. $ mathcal A(0,0,1)=(0,0,0) $ и ни при каком выборе оператора $ mathcal B $ нельзя добиться выполнения равенства $ mathcal B(0,0,0)=(0,0,1) $. ♦

Показать, что обратным для оператора

$$fracint_0^x : p(x) longmapsto fracint_^ p(t) d, t ,$$ на $ mathbb P_ $ является оператор $$ fracleft(xtimes Box right) : p(x) longmapsto (xp(x))’ .$$

Теорема 4. Оператор $ mathcal A_ $ обратим тогда и только тогда, когда когда он невырожден: $ operatorname (mathcal A) =0 $. В этом случае $ mathcal A^ $ единствен и коммутирует с $ mathcal A $.

При $ Kin mathbb N $ и $ K>1 $, $ K_ $-я степень оператора $ mathcal A $ определяется рекурсивной формулой $$mathcal A^=mathcal A (mathcal A^) .$$ Если, вдобавок, $ mathcal A $ невырожден, то отрицательная степень оператора определяется формулой $$mathcal A^=left(mathcal A^right)^K . $$ Полагают также $ mathcal A^= $ для любого $ mathcal A ne $.

Теорема 5. Степени оператора $ mathcal A $ коммутируют:

$$mathcal A^ mathcal A^=mathcal A^mathcal A^=mathcal A^ .$$

Пример. $ K_ $-й степенью оператора дифференцирования в пространстве полиномов $ mathbb P_ $ будет оператор нахождения $ K_ $-й производной:

$$left( frac right)^K = frac .$$ Очевидно, что при $ K_>n $ этот оператор будет нулевым. ♦

Пример. В произвольном пространстве $ mathbb V_ $ разбитом в прямую сумму нетривиальных подпространств $ mathbb V= mathbb V_1 oplus mathbb V_2 $ оператор проецирования $ mathcal P $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_2 $ обладает свойством $ mathcal P^2 = mathcal P $ (проецирование проекции оставляет ее на месте). ♦

Оператор $ mathcal A $, обладающий свойством $ mathcal A^2 = mathcal A $, называется идемпотентным 3) .

Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ отображение $ mathcal A_ $ действует по правилу

$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Для этого оператора $ K_ $-й его степенью является оператор $$ mathcal B (f(x)) = f(x) (x^2-2)^K pmod . $$ Действительно, если $$ f(x)(x^2-2) equiv q(x)(x^4-x^3-x^2+x)+ r(x) $$ при $ subset mathbb R[x] $ и $ deg r(x) le 3 $, то $$ f(x)(x^2-2)^2 equiv q(x)(x^4-x^3-x^2+x)(x^2-2)+ r(x)(x^2-2) . $$ Но тогда $$ mathcal A^2 (f(x))= mathcal A (r(x)) = r(x) (x^2-2) pmod equiv $$ $$ equiv f(x)(x^2-2)^2 pmod . $$ Завершает доказательство святая индукция по степени $ K_ $… ♦

Пусть задан произвольный полином $ g(x)=b_x^m+b_1x^+dots+b_m $ из $ mathbb R[x] $ или $ mathbb C[x] $. Выражение $$g(mathcal A )= b_0mathcal A^+b_1mathcal A^+dots+b_m$$ будем называть операторным полиномом.

Доказать, что операторные полиномы коммутируют: $ g_1(mathcal A )g_2(mathcal A )=g_2(mathcal A )g_1(mathcal A ) $.

Доказать, что для любого $ mathcal A in om(mathbb V,mathbb V) $ всегда найдется полином $ g_(x) $, $ deg g le n^2+1 $ такой, что $ g(mathcal A)= $.

Сформулируем еще один результат, являющийся частным случаем приведенного в пункте ☞ СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.

Теорема 6. Пусть $ $ — произвольный базис $ mathbb V_ $, а $ Y_1,Y_2,dots,Y_n $ — произвольные векторы того же пространства. Существует единственный оператор $ mathcal A: mathbb V longmapsto mathbb V $ такой, что

$$ mathcal A(X_1)=Y_1,mathcal A(X_2)=Y_2, dots,mathcal A(X_n)=Y_n .$$

Доказательство. Искомый оператор строится следующим образом. Если $ X=x_1X_1+x_2X_2+dots+x_nX_n $ — разложение произвольного вектора $ X in mathbb V $ по базису, то $$ mathcal A(X)=x_1 Y_1+x_2Y_2+dots+ x_nY_n . $$ Единственность этого оператора доказывается от противного. Любой другой оператор $ mathcal B $, удовлетворяющий условиям $ _^n $, будет действовать на тот же вектор $ X_ $ с тем же результатом: $$ mathcal B(X)=x_1 mathcal B(X_1)+x_2mathcal B(X_2) +dots+ x_nmathcal B(X_n)= x_1 Y_1+x_2Y_2+dots+ x_nY_n= mathcal A(X) . $$ ♦

Таким образом, оператор — как функция, действующая в $ n_ $-мерном линейном пространстве, однозначно определяется заданием на $ n_ $ линейно независимых векторах. В доказательстве теоремы дается и конструктивный способ представления оператора по этим значениям (т.е. строится его «интерполяционная формула» ).

Видео:Симметрия относительно точки, относительно прямой и относительно плоскостиСкачать

Матрица оператора

Рассмотрим оператор $ mathcal A $ на $ mathbb V_ $ и пусть $ $ — базис $ mathbb V_ $. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от рассмотренного в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для $ mathcalm (mathcal A) $. Поскольку $ mathcalm (mathcal A) $ является подпространством $ mathbb V_ $, то было бы слишком большой роскошью иметь два разных базиса для одного и того же пространства.

Найдем координаты образов базисных векторов $ mathcal A (X_1),dots,mathcal A (X_n) $ в том же базисе $ $: $$ left< begin mathcal A(X_1)&=& <<coloralpha >>_X_1+ <<coloralpha >>_X_2+dots+ <<coloralpha >>_X_n, \ mathcal A(X_2)&=& <<coloralpha >>_X_1+ <<coloralpha >>_X_2+dots+ <<coloralpha >>_X_n, \ dots & & qquad dots , \ mathcal A(X_n)&=&alpha_X_1+alpha_X_2+dots+alpha_X_n. end right. $$ Матрица $$ mathbf A= left(begin <<coloralpha >>_ & <<coloralpha >>_& dots & alpha_ \ <<coloralpha >>_ & <<coloralpha >>_& dots & alpha_ \ dots & & & dots \ <<coloralpha >>_ & <<coloralpha >>_& dots & alpha_ end right)_, $$ в столбцах которой стоят координаты образов базисных векторов, называется матрицей оператора $ mathcal A_ $ в базисе $ $.

Пример. Известны образы базисных векторов $ mathbb R^ $ под действием оператора $ mathcal A_ $:

$$mathcal A left( begin 5 \ 3 \ 1 endright)= left( begin -2 \ 1 \ 0 endright) , mathcal A left( begin 1 \ -3 \ -2 endright) = left( begin -1 \ 3 \ 0 endright) , mathcal A left( begin 1\ 2 \ 1 endright)= left( begin -2 \ -3 \ 0 endright) . $$ Найти матрицу этого оператора в исходном базисе.

Решение. Элементы матрицы $ $ ищутся по формулам из определения, которые можно переписать в матричном виде: $$left[ X_1,dots,X_n right] =left[ mathcal A (X_1),dots,mathcal A (X_n) right] .$$ Откуда $$= left[ X_1,dots,X_n right]^ left[ mathcal A (X_1),dots,mathcal A (X_n) right] ,$$ и для нашего примера эта формула дает $$ = left(begin 5&1&1 \ 3&-3&2 \ 1&-2&1 endright)^ left(begin -2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = $$ $$ =left(begin 1&-3&5\ -1&4&-7\ -3&11&-18 endright) left(begin -2&-1&-2 \ 1&3&-3 \ 0&0&0 endright) = left(begin -5&-10&7\ 6&13&-10\ 17&36&-27 end right). $$ ♦

В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_ $ действует по правилу

$$ mathcal A (f(x)) = f(x) (x^3+2,x^2+1) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^3+2,x^2+1) $ на $ x^4+4 $. Найти матрицу оператора $ mathcal A_ $ в базисе $ $.

Ответ. $$ left(begin 1 & -4 & -8 & 0 \ 0 & 1 & -4 & -8 \ 2& 0 & 1 & -4 \ 1 & 2 & 0 & 1 end right) . $$

Теорема 1. Координаты произвольного вектора $ X=x_1X_1+dots+x_nX_n $ и его образа $ Y=mathcal A(X)=y_1X_1+dots+y_nX_n $ связаны формулой

$$ left(begin y_1 \ vdots \ y_n end right) = left(begin x_1 \ vdots \ x_n end right) . $$

Как изменяется матрица оператора при переходе к новому базису?

Доказательство ☞ ЗДЕСЬ.

Пример. Оператор $ mathcal A $ в базисе пространства $ mathbb R^ $

Матрицы $ $ и $ $, связанные соотношением $ =C^cdot cdot C $ при какой-то неособенной матрице $ C_ $, называются подобными, этот факт будем записывать: $ doteq $.

Доказать, что отношение подобия есть отношение эквивалентности, и если $ doteq $ то $ g()doteq g() $ при любом полиноме $ g_(x) $.

Теорема 3. Для оператора $ mathcal A_ $ ранг его матрицы является инвариантом, т.е. не зависит от выбора базиса пространства. Этот ранг совпадает с рангом оператора $ mathcal A_ $.

Доказательство. Если $ $ и $ $ — матрицы оператора в двух разных базисах, то они являются подобными: $ =C^ C $. По свойству ранга матрицы имеем: $ operatorname( )= operatorname() $. ♦

Дефект оператора $ mathcal A_ $ совпадает с дефектом его матрицы в произвольном базисе пространства.

Теорема 4. Для оператора $ mathcal A_ $ определитель и след его матрицы являются инвариантами, т.е. не зависят от выбора базиса пространства.

Доказательство. Действительно, для подобных матриц $ $ и $ $, на основании теоремы Бине-Коши имеем: $$ det () = det (C^ C) = det (C^) cdot det () cdot det (C) =det () . $$ Далее, по свойству следа матрицы: $$ operatorname() = operatorname(C^ C)=operatorname( cdot C cdot C^)=operatorname() . $$ ♦

Этот результат позволяет ввести понятие определителя и следа оператора $ mathcal A_ $ — посредством матрицы этого оператора в произвольном базисе пространства. Такое определение оказывается корректным поскольку оба значения не зависят от выбора базиса.

Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения 4) объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.

Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.

Теорема 6. Линейное пространство $ om(mathbb V,mathbb V) $ операторов на $ mathbb V_, dim mathbb V = n $ изоморфно линейному пространству квадратных матриц порядка $ n_ $ (с элементами из $ mathbb R_ $ или из $ mathbb C_ $).

Это утверждение является простым следствием теоремы 2, приведенной в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ. Однако в случае операторов установленный изоморфизм сохранит не только результат операции сложения, но и результат операции умножения: $$ . mbox mathcal A_1 leftrightarrow mathbf A_1, mathcal A_2 leftrightarrow mathbf A_2, mbox mathcal A_1+ mathcal A_2 leftrightarrow mathbf A_1 + mathbf A_2, lambda mathcal A_1 leftrightarrow lambda mathbf A_1 , mathcal A_1 mathcal A_2 leftrightarrow mathbf A_1 mathbf A_2 . $$ Я сформулирую этот «усиленный вариант» изоморфизма в виде набора свойств, которыми буду пользоваться по мере возникновения потребности.

Теорема 7. В любом базисе пространства

а) матрица нулевого оператора $ mathcal O $ является нулевой матрицей $ mathbb O_ $, а матрица тождественного оператора $ mathcal E $ является единичной матрицей $ E_ $; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);

б) матрица произведения операторов совпадает с произведением матриц этих операторов 5) ;

в) коммутирующим операторам соответствуют коммутирующие матрицы;

г) если $ $ — матрица оператора, то $ ^ $ — матрица обратного оператора;

д) если $ $ — матрица оператора $ mathcal A $, то матрицей операторного полинома $ g (mathcal A) $ является матрица $ g() $ .

Матрица оператора и матрица перехода от базиса к базису

Эти матрицы как-то взаимодействовали между собой в предыдущем пункте, хотя вторая была определена совершенно в другом разделе. Обе матрицы квадратные, обе имеют в определении «завязку» на базис пространства $ mathbb V_ $. У начинающих изучать теорию часто возникает путаница при различении этих определений.

«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).

Тем не менее, с чисто формальной точки зрения, матрица $ C_ $ перехода от базиса $ $ пространства $ mathbb V_ $ к какому-то другому базису $ $ того же пространства может считаться матрицей некоторого оператора, действующего в этом пространстве. В самом деле, на основании теоремы, приведенной в конце ☞ ПУНКТА, существует единственный оператор $ mathcal C $, переводящий старые базисные векторы в новые, взятые в той же последовательности: $$ mathcal C (X_1)=mathfrak X_1, mathcal C (X_2)= mathfrak X_2, dots, mathcal C (X_n)= mathfrak X_n . $$ Но тогда, по определению, матрица оператора $ mathcal C $ в базисе $ $ совпадает с матрицей $ C_ $ перехода от базиса $ $ к базису $ $.

Я буду записывать матрицы операторов и матрицы переходов от базиса к базису в разных стилях: $ mathbf A, mathbf B,dots $ и, соответственно, $ C, P, T, dots $ — с целью быстрого распознавания их «физической» сущности.

Матрица оператора проецирования

Настоящий пункт может быть пропущен при первоначальном чтении.

Теорема. Рассмотрим линейную оболочку линейно независимой системы столбцов $ subset mathbb R^n $.

$$ mathbb M =left < lambda_1 Y_1 + dots + lambda_k Y_k big| subset mathbb R right>= mathcal L (Y_1,dots,Y_k) , . $$ Пусть скалярное произведение векторов $ X_ $ и $ Y_ $ задается стандартным способом, т.е. $ langle X,Y rangle =x_1y_1+dots+x_ny_n $. Ближайшей к точке $ X_0 subset mathbb R^n $ точкой многообразия (или ортогональной проекцией точки $ X_0 $ на многообразие) $ mathbb M_ $ является $$ X_ = mathbf L (mathbf L^ mathbf L )^ mathbf L^ X_0 , . $$ Здесь $ mathbf L=[Y_1 |dots |Y_k]_ $.

Доказательство. Пусть $ X_0=X_0^<^>+X_0^<^> $, где $ X_0^<^> $ — ортогональная проекция точки $ X_0 $ на $ mathbb M $, а $ X_0^<^> $ — ортогональная составляющая. Тогда $$ mathbf L^ X_0^<^>=mathbb O $$ поскольку $ Y_1^ X_0^<^>=0,dots, Y_k^ X_0^<^>=0 $. Далее, $ X_0^<^> $ можно разложить по базису $ $: $$ X_0^<^>=alpha_1 Y_1+dots+ alpha_k Y_k quad npu quad subset mathbb R , . $$ Следовательно, $$ mathbf L^ X_0=mathbf L^ (X_0^<^>+X_0^<^>)=mathbf L^ X_0^<^>= mathbf L^ (alpha_1 Y_1+dots+ alpha_k Y_k)= $$ $$ =left( begin alpha_1 Y_1^ Y_1 +dots + alpha_k Y_1^ Y_k \ alpha_1 Y_2^ Y_1 +dots + alpha_k Y_2^ Y_k \ dots \ alpha_1 Y_k^ Y_1 +dots + alpha_k Y_k^ Y_k end right)= mathbf L^ mathbf L left( begin alpha_1 \ alpha_2 \ vdots \ alpha_k end right), . $$ Тогда $$ mathbf L (mathbf L^ mathbf L )^ mathbf L^ X_0= mathbf L left( begin alpha_1 \ alpha_2 \ vdots \ alpha_k end right) =alpha_1 Y_1+dots+ alpha_k Y_k= X_0^<^> , . $$ На основании теорем $ 1_ $ и $ 2_ $, приведенных ☞ ЗДЕСЬ, точка $ X_0^<^> $ является ближайшей точкой многообразия $ mathbb M $ к точке $ X_ $. ♦

Матрица $ P=mathbf L (mathbf L^ mathbf L )^ mathbf L^ $ является матрицей оператора ортогонального проецирования на многообразие $ mathbb M_ $ в стандартном базисе $$ bigg<_j = big[underbrace_,0,dots,0big]^ bigg>_^n , . $$ Она симметрична и идемпотентна, т.е. обладает свойством $ P^2=P $.

Пример. В $ mathbb R^ $ найти матрицу проецирования на плоскость $ x+y+z=0 $.

Решение. Параметрическое задание плоскости: $$ mathbb M=< lambda_1 underbrace<[1,-1,0]^>_ + lambda_2 underbrace<[0,1,-1]^>_ big| subset mathbb R > , . $$ Имеем: $$ mathbf L= left(begin 1 & 0 \ -1 & 1 \ 0 & -1 end right) Rightarrow mathbf L^ mathbf L= left(begin 2 & -1 \ -1 & 2 end right) Rightarrow (mathbf L^ mathbf L )^= left(begin 2/3 & 1/3 \ 1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow mathbf L (mathbf L^ mathbf L )^ mathbf L^= frac left(begin 2 & -1 & -1 \ -1& 2 & -1 \ -1 & -1 & 2 end right) , . $$ ♦

Матрица оператора отражения (оператора Хаусхолдера)

Настоящий пункт может быть пропущен при первоначальном чтении.

В пространстве $ mathbb R^n $ со стандартным скалярным произведением рассмотрим плоскость, заданную уравнением $$ C^X= c_1x_1+c_2x_2+dots+c_nx_n = 0 $$ при векторе нормали $ C^=(c_1,c_2,dots,c_n) $ единичной длины: $ |C|^2= C^C=1 $. Действие оператора зеркального отражения или оператора Хаусхолдера 6) относительно этой плоскости на вектор (точку) $ X in mathbb R^n $ определим правилом $$ mathcal H( X^<^> + X^<^>)= X^<^> — X^<^> ; $$ здесь $ X^<^> $ — ортогональная проекция вектора $ X_ $ на заданную плоскость, а $ X^<^> $ — ортогональная составляющая вектора $ X_ $ относительно этой плоскости.

Теорема. Оператор $ mathcal H $ задается уравнением

$$ mathcal H(X)=X-2, langle X,C rangle C=X-2, C (C^X)= X-2, C^XC , . $$

Доказательство. $$ mathcal H( X^<^> + X^<^>)=X^<^> + X^<^>-2, langle X^<^>,C rangle C-2, langle X^<^>,C rangle C = $$ Поскольку $ X^<^> $ ортогонален, а вектор $ X^<^> $ коллинеарен вектору $ C $ единичной длины, то $$= X^<^> + X^<^> — 2, X^<^> = X^<^> — X^<^> , . $$ ♦

Теорема. Матрица оператора $ mathcal H $ в стандартном базисе

$$ bigg<_j = big[underbrace_,0,dots,0big]^ bigg>_^n , . $$ имеет вид $$ mathbf H_= E-2, C cdot C^ = left( begin 1-2c_1^2 & -2,c_1c_2 & dots & — 2 c_1 c_n \ -2,c_1c_2 & 1-2c_2^2 & dots & — 2 c_2 c_n \ vdots & & & vdots \ — 2 c_1 c_n & — 2 c_2 c_n & dots & 1-2c_n^2 end right) , . $$

Пример. Найти зеркальное отражение точки $ [3,2,3] $ относительно плоскости $ 2,x-2,y+z = 0 $.

Решение. Здесь $ C^=[2/3,-2/3,1/3] $ и $$ mathcal H(X)= left( begin 3 \ 2 \ 3 end right) — 2([3,2,3],[2/3,-2/3,1/3]) left( begin 2/3\ -2/3 \ 1/3 end right)= left( begin 7/9 \ 38/9 \ 17/9 end right) , . $$ Проверим результат посредством матричного представления: $$ mathbf H_C= left( begin 1/9 & 8/9 & -4/9 \ 8/9 & 1/9 & 4/9 \ -4/9 & 4/9 & 7/9 end right) quad Rightarrow quad mathbf H left( begin 3 \ 2 \ 3 end right)= left( begin 7/9 \ 38/9 \ 17/9 end right) , . $$ ♦

Матрица $ mathbf H_ $ одновременно симметрична и ортогональна, и $ det mathbf H_=-1 $. Следовательно, ей обратная существует и совпадает с ней самой: $$ mathbf H_^= mathbf H_ , . $$

Видео:Уравнение плоскости через 2 точки параллельно векторуСкачать

Инвариантное подпространство

Задача. Подобрать базис пространства $ mathbb V_ $ так, чтобы матрица заданного оператора $ mathcal A_ $ имела наиболее простой вид.

Исследуем действие оператора $ mathcal A $ на произвольное подпространство $ mathbb V_1 subset mathbb V $: $$mathcal A (mathbb V_1)= left .$$ Вообще говоря, множества $ mathbb V_1 $ и $ mathcal A (mathbb V_1) $ будут различными, т.е. $ exists X_1 in mathbb V_1 $ такой, что $ mathcal A (X_1)notin mathbb V_1 $.

Подпространство $ mathbb V_1 $ называется инвариантным подпространством оператора $ mathcal A $, если оно отображается этим оператором в себя: $$ mathcal A(mathbb V_1)subset mathbb V_1 .$$

$ mathbb V_1= $ и $ mathbb V_1=mathbb V $ — тривиальные инвариантные подпространства произвольного оператора $ mathcal A $.

Нас будут интересовать нетривиальные инвариантные подпространства.

Пример. Оператор

$$left(begin x \ y \ z end right) longmapsto left(begin / & -/ & 0 \ / & / & 0 \ 0 & 0 & 1 end right) left(begin x \ y \ z end right) $$ задает в пространстве поворот вокруг оси $ mathbb O z $ на угол $ +pi /4 $. Нетривиальными инвариантными подпространствами будут

а) ось вращения $ mathbb V_1=<(0,0,z)^<^> mid z in mathbb R> $, $ dim mathbb V_1=1 $ и

б) плоскость, перпендикулярная оси вращения $ mathbb V_2=<(x,y,0)^<^> mid subset mathbb R> $, $ dim mathbb V_2= 2 $. ♦

Пример. Оператор

$$left(begin x \ y end right) longmapsto left(begin lambda_1 x \ lambda_2 y end right) $$ задает на плоскости «растяжение»: $ x_ $-компонента увеличивается в $ lambda_ $ раз, а $ y_ $-компонента — в $ lambda_ $ раз. При любой комбинации коэффициентов растяжения координатные оси будут инвариантными подпространствами. Однако в частном случае $ lambda_1=lambda_2 $ инвариантной будет также любая прямая, проходящая через начало координат. ♦

Пример. Оператор в $ mathbb R^_ $ задан блочной матрицей

$$X longmapsto left( begin _1 & \ mathbb O & _2 end right) X $$ где $ _1 $ — $ n_1times n_1 $-матрица, $ _2 $ — $ (n-n_1)times (n-n_1) $-матрица. Множество столбцов $$mathbb V_1=left<X=[x_1,dots,x_,0,dots,0]^<^> bigg| < x_1, dots, x_> subset mathbb R right>$$ образует инвариантное подпространство, $ dim mathbb V_1=n_1 $. Если же, вдобавок, матрица, обозначенная $ $ — нулевая, то вторым инвариантным подпространством будет $$ mathbb V_2=left<X=[0,dots,0,x_,dots,x_n]^<^> bigg| <x_,dots, x_n > subset mathbb R right> .$$ ♦

Теорема. $ mathcaler (mathcal A) $ и $ mathcalm(mathcal A) $ — инвариантные подпространства оператора $ mathcal A $.

Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.

Теорема. Если пространство $ mathbb V_ $ раскладывается в прямую сумму подпространств, инвариантных относительно оператора $ mathcal A $, то существует базис пространства, в котором матрица оператора будет блочно-диагональной.

Теорема обобщается очевидным образом на произвольное число слагаемых подпространств: $ mathbb V=mathbb V_1oplus mathbb V_2 oplus dots oplus mathbb V_k $. Если при этом $ dim mathbb V_1= dots = dim mathbb V_k=1 $, то матрица оператора в базисе, полученном объединением базисных векторов слагаемых подпространств, становится диагональной — это и является решением задачи, поставленной в начале пункта.

Видео:Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Собственное число и собственный вектор

Задача. Найти одномерные инвариантные подпространства оператора.

Вектор $ X_in mathbb V $ называется собственным вектором оператора $ mathcal A_ $, если $$ X ne mathbb O, quad u quad exists lambda in mathbb C qquad mbox qquad mathcal A(X)=lambda X .$$ В этом случае число $ lambda_ $ называется собственным или характеристическим числом оператора, соответствующим (или принадлежащим) данному собственному вектору; обратно, говорят, что вектор $ X_ $ принадлежит собственному числу $ lambda_ $.

Пример. Оператор

$$left(begin x \ y end right) longmapsto left(begin 1 & — 5/2 \ -1/2 & 2 end right) left(begin x \ y end right) $$ задает отображение плоскости $ mathbb R^2 $. На рисунке показан результат действия этого отображения на единичную окружность. Все точки плоскости, за исключением начала координат $ mathbb O_ $, изменят свое положение — ни одна не останется на месте.

Если рассмотреть эти точки как концы векторов, имеющих начало в $ mathbb O_ $, то смещения точек под действием оператора можно представить в виде двух составляющих: растяжения (т.е. увеличения расстояния до начала координат) и поворота вокруг начала координат на некоторый угол. И только по двум направлениям плоскости поворота не происходит. Точки окружности с координатами $$ pm left( 0.823, -0.568 right)^ quad u quad pm left( 0.960, 0.278 right)^ $$ будут смещаться без поворота. Эти точки и задают координаты конца собственного вектора. А соответствующие им собственные числа $ 2.725 $ и $ 0.275 $ определяют коэффициенты сдвига. Если вообразить оператор как деформацию физической среды, заполняющей плоскость, то можно сказать, что cобственный вектор задает направление, на котором действие оператора сводится к растяжению, при этом коэффициент растяжения и будет собственным числом.

Анимация процесса ☞ ЗДЕСЬ (1500 Kb, gif).

Пример другого оператора $$ left(begin x \ y end right) longmapsto left(begin 1 & — 3 \ 1 & -1 end right) left(begin x \ y end right) $$ показывает, что существование вещественных собственных чисел вовсе не гарантировано даже в случае оператора в вещественном пространстве: в этом примере все точки плоскости повернутся вокруг начала координат. ♦

Доказать, что $ operatorname (mathcal A) ne 0 $ тогда и только тогда, когда оператор $ mathcal A_ $ имеет собственное число, равное нулю.

Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства оператора является собственным вектором.

Пример. В пространстве $ mathbb P_3 $ полиномов с вещественными коэффициентами степени $ le 3 $ оператор $ mathcal A_ $ действует по правилу

$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ т.е. полином $ f_(x) $ отображается в остаток от деления произведения $ f(x) (x^2-2) $ на $ x^4-x^3-x^2+x $. Найти собственные векторы этого оператора.

Решение. В пространстве $ mathbb P_3 $ векторами являются полиномы, а условие того, что полином $ f_(x) $ является собственным, принадлежащим числу $ lambda_ $, записывается в виде: $$ f(x)(x^2-2)equiv lambda f(x) pmod quad iff $$ $$ iff quad f(x)(x^2-2-lambda)equiv 0 pmod . $$ Поскольку $ deg f le 3 $, то последнее может выполняться тогда и только тогда, когда полином $ x^2-2-lambda $ имеет общие корни с $ x^4-x^3-x^2+x equiv x(x+1)(x-1)^2 $. Из этого условия вытекает, что число $ lambda_ $ может принимать только два значения: $ lambda_1=-2 $ и $ lambda_2=-1 $. Если $ lambda_1=-2 $ является собственным числом, то ему соответствующий собственный вектор — полином степени $ le 3 $ — должен определяться из условия делимости $ f(x)x^2 $ на $ x(x+1)(x-1)^2 $. Такой полином имеет вид $ t(x+1)(x-1)^2 $ при произвольной константе $ t_ $. Следовательно множество $$ $$ является множеством собственных векторов, принадлежащих $ lambda_1=-2 $.

С числом $ lambda_2=-1 $ поступаем аналогично. Условие делимости полинома $ f(x)(x^2-1) $ на $ x(x+1)(x-1)^2 $ дает также бесконечное множество: $$ < (t_1x+t_2)x(x-1) mid subset mathbb R > . $$ Однако в этом случае бесконечность множества качественно иная, чем в предыдущем случае; она — «двумерная». ♦

Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.

Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.

Уравнение $ det (-lambda E)= 0 $ называется характеристическим или вековым уравнением, а полином в левой его части — характеристическим полиномом матрицы $ $. Любой корень характеристического полинома матрицы называется собственным числом этой матрицы. Набор всех собственных чисел матрицы (корней характеристического полинома с учетом кратностей) называется спектром матрицы. Ненулевой вектор $ X in mathbb C^n $, удовлетворяющий условию $ X= lambda X $, где $ lambda $ — собственное число матрицы, называется собственным вектором матрицы, соответствующим (или принадлежащим) данному собственному числу.

Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.

Решение. Базисом в пространстве $ mathbb P_3 $ выберем $ $. Образы базисных векторов под действием оператора $ mathcal A (f(x)) = f(x) (x^2-2) pmod $: $$ left<begin mathcal A (1) =&-2& &+x^2& ,\ mathcal A (x) =&&-2,x &&+x^3 ,\ mathcal A (x^2) =& &-x &-x^2 &+x^3, \ mathcal A (x^2) =& &-x & & , end right. qquad Rightarrow qquad = left(begin -2 & 0 & 0 & 0 \ 0 & -2 & -1 & -1 \ 1& 0 & -1 & 0 \ 0 & 1 & 1 & 0 end right) . $$ Характеристический полином матрицы $ $: $$ left|begin -2-lambda & 0 & 0 & 0 \ 0 & -2-lambda & -1 & -1 \ 1& 0 & -1-lambda & 0 \ 0 & 1 & 1 & -lambda end right|equiv (lambda+2)(lambda^3+3,lambda^2+3,lambda+1)equiv (lambda+2)(lambda+1)^3 . $$ Собственные числа $ lambda_1=-2 $ и $ lambda_2=-1 $, спектр матрицы $ $. Подставляем каждое из собственных чисел в матрицу $ -lambda E $ и решаем получившиеся системы однородных уравнений. Поскольку каждая из них должна иметь бесконечное множество решений, то мы строим фундаментальные системы решений (ФСР) $$ begin & (-lambda E)X=mathbb O & \ <colorswarrow > & & <colorsearrow > \ lambda_1=-2 & & lambda_2=-1 \ Downarrow & & Downarrow \ left(begin 0 & 0 & 0 & 0 \ 0 & 0 & -1 & -1 \ 1& 0 & 1 & 0 \ 0 & 1 & 1 & 2 end right) left(begin x_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O & & left(begin -1 & 0 & 0 & 0 \ 0 & -1 & -1 & -1 \ 1& 0 & 0 & 0 \ 0 & 1 & 1 & 1 end right) left(begin x_1 \ x_2 \ x_3 \ x_4 end right)= mathbb O . \ <colorDownarrow > & & <colorDownarrow > \ x_1=1,x_2=-1,x_3=-1,x_4=1 & & left<begin x_1=0,x_2=-1,x_3=1,x_4=0 \ x_1=0,x_2=-1,x_3=0,x_4=1 end right> end $$ Таким образом, собственному числу $ lambda_1=-2 $ соответствует собственнный вектор — полином $ 1-x-x^2+x^3 $, и он полностью совпадает с полученным при решении предыдущего примера. В то же время собственному числу $ lambda_2=-1 $ соответствует два линейно независимых собственнных вектора — полиномы $ -x+x^2 $ и $ -x+x^3 $. Любой (не тождественно нулевой) полином множества $$ < tau_1(-x+x^2) +tau_2(-x+x^3) mid subset mathbb R > $$ будет также являться собственным, принадлежащим $ lambda_2=-1 $. Это множество также совпадает с полученным при решении предыдущего примера. ♦

Итак, два формально различных подхода к решению одного и того же примера не привели к противоречию. Хотелось бы, однако, гарантировать глобальную непротиворечивость определения собственных чисел и векторов — т.е. независимость (инвариантность) этих объектов относительно способов их нахождения, и, в частности, от выбора базиса пространства $ mathbb V_ $.

Теорема. Характеристические полиномы подобных матриц одинаковы.

Доказательство. $ doteq iff exists $ неособенная матрица $ C_ $, такая что $ =C^ C $. Имеем: $$det (-lambda E)=det (C^ C-lambda E)=$$ $$= det (C^ C-lambda C^EC)=det left[ C^ ( -lambda E)C right] = det (-lambda E) .$$ ♦

Иначе говоря, для оператора $ mathcal A_ $ характеристический полином его матрицы не зависит от выбора базиса пространства. Поэтому можно говорить о характеристическом полиноме оператора $ mathcal A_ $.

Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.

Пример. Для рассмотренного в предыдущих примерах оператора

$$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ действующего в $ mathbb P_3 $, характеристический полином равен

$$ lambda^4+5,lambda^3+9,lambda^2+7,lambda+2 , .$$ Проверим утверждение теоремы Гамильтона-Кэли — должно быть выполнено условие $$ mathcal A^4+5,mathcal A^3+9,mathcal A^2+7,mathcal A +2, mathcal E = mathcal O . $$ Степени данного оператора $ mathcal A_ $ обсуждались в примере ☞ ПУНКТА. Переписанное в терминах остатков, последнее условие превращается в $$ (x^2-2)^4f(x)+5,(x^2-2)^3f(x)+9,(x^2-2)^2f(x)+7,(x^2-2)f(x) + $$ $$+2,f(x) equiv 0 pmod , $$ т.е. полином, стоящий в левой части сравнения, должен делиться нацело на $ x^4-x^3-x^2+x $ при любом выборе полинома $ f_(x) $. Проверяем: $$ (x^2-2)^4+5,(x^2-2)^3+9,(x^2-2)^2+7,(x^2-2)+2 equiv $$ $$equiv x^8-3,x^6+3,x^4-x^2 equiv (x^4+x^3-x^2-x)(x^4-x^3-x^2+x) , $$ т.е. утверждение оказывается справедливым. ♦

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Диагонализуемость матрицы оператора

Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.

Теорема 2. Если оператор имеет $ n=dim mathbb V $ линейно независимых собственных векторов, то в базисе ими образуемом матрица оператора диагональна. Обратно: если матрица оператора в некотором базисе диагональна, то каждый вектор этого базиса является собственным для оператора.

Базис линейного пространства, состоящий из собственных векторов оператора $ mathcal A_ $, называется каноническим.

[Матричная версия теоремы]. Пусть $ A_ $ — квадратная матрица. Неособенная матрица $ C_ $, удовлетворяющая равенству

$$C^ A C= A_ quad mbox A_ quad mbox $$ существует тогда и только тогда, когда существует базис пространства $ mathbb C^_ $, состоящий из собственных векторов матрицы $ A_ $. Тогда матрица $ C_ $ является матрицей перехода от стандартного базиса $$ bigg<_j = big[underbrace_,0,dots,0big]^ bigg>_^n $$ к каноническому, а на диагонали $ A_ $ стоят собственные числа матрицы $ A_ $: $$ A_= left( begin lambda_1 & 0 & dots & 0 \ 0 & lambda_2 & dots & 0 \ & & ddots & \ 0 & 0 & dots & lambda_n end right) . $$

Доказательство. Проведем формальное доказательство данного конкретного частного случая. Рассмотрим матричное равенство $$ A C= CA_ $$ при некоторой диагональной матрице $ A_ $. Легко видеть, что оно эквивалентно системе равенств относительно столбцов матрицы $ C_ $: $$ AC_=d_1 C_,dots, AC_=d_n C_ , . $$ Если все столбцы $ < C_>_^n $ ненулевые, то тогда они являются собственными векторами для матрицы $ A_ $, а числа $ < d_>_^n $ — собственными числами, соответствующими этим собственным векторам. Если матрица $ C_ $ невырождена, то все ее столбцы линейно независимы. Но тогда они образуют базис пространства $ mathbb C^n $, состоящий из собственных векторов. Обратное тоже верно. ♦

При выполнении условия предыдущего следствия говорят, что матрица $ A_ $ диагонализуема или приводится к диагональной форме 7) .

Теорема позволяет сформулировать достаточное условие диагонализуемости.

Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.

Это условие не является необходимым, как показывает пример тождественного оператора .

Случай существования кратного корня у характеристического полинома является «пограничным»: существуют примеры как диагонализуемых, так и недиагонализуемых матриц. Так, для матриц $$ A= left( begin 0 &1 \ -1 &2 end right) quad mbox quad A= left( begin 1 &0 \ 1&1 end right) $$ при попытке подобрать матрицу $ C_ $, удовлетворяющую равенству $$AC=C left( begin alpha_1 &0 \ 0 & alpha_2 end right) qquad npu forall subset mathbb C $$ получим: $ det C=0 $.

В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.

Теорема 4. Множество собственных векторов оператора, принадлежащих его собственному числу $ lambda_^ $ , дополненное нулевым вектором, образует линейное подпространство пространства $ mathbb V_ $.

Это подпространство $$ mathbb V_ = mathcaler (mathcal A- lambda_ mathcal E) $$ пространства $ mathbb V_ $ называется собственным подпространством оператора, соответствующим $ lambda_^ $. Величина $$ dim (mathcaler (mathcal A- lambda_ mathcal E)) $$ называется геометрической кратностью собственного числа $ lambda_^ $. Можно доказать, что геометрическая кратность собственного числа не превосходит кратности собственного числа в характеристическом полиноме. Для акцентирования различий в определениях двух кратностей, кратность собственного числа в характеристическом полиноме называют еще алгебраической кратностью собственного числа.

Если оператор (в некотором базисе пространства) задан своей матрицей $ mathbf A^ $, то базисные векторы собственного подпространства $ mathbb V_ $ вычисляются посредством нахождения фундаментальной системы решений (ФСР) системы линейных уравнений $$ (mathbf A- lambda_ E) X=mathbb O . $$

Теорема 5. Матрица оператора диагонализуема тогда и только тогда, когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:

Диагонализуема ли матрица оператора $$ mathcal A (f(x)) = f(x) (x^2-2) pmod , $$ рассмотренного в примерах предыдущего пункта?

Пример. Найти все вещественные значения параметра $ <color > $, при которых матрица

Решение. Характеристический полином $ f(lambda)=-lambda^3+3, lambda-2,(3, <color > -1) $ имеет кратные корни только тогда когда его дискриминант $ mathcal D(f)=-324, <color > (3, <color > -2) $ обращается в нуль. При $ <color > =0 $ корень $ lambda=-1 $ имеет алгебраическую кратность $ 2_ $. Найдем дефект матрицы $ A+E $: $$left( begin 2 &0 & -2 \ -1 &3 &1 \ 2 & 0 & -2 end right) longrightarrow left( begin 1 &0 & -1 \ 0 &3 &0 \ 0 & 0 & 0 end right) Longrightarrow operatorname (A+E) =2 Longrightarrow operatorname (A+E)=1 . $$ Таким образом, геометрическая кратность собственного числа $ lambda=-1 $ равна $ 1_ $ и условие теоремы $ 5 $ не выполнено. Оно не будет выполнено и при $ <color > = 2/3 $ (здесь корень $ lambda=1 $ имеет кратность $ 2_ $).

Ответ. Матрица диагонализуема при всех значениях параметра, за исключением $ <color > = 0 $ и $ <color > = 2/3 $.

Диагонализуемость матрицы оператора над полем вещественных чисел

В предыдущем пункте мы рассматривали операторы, не всегда акцентируя внимания на поле, над которым они были определены — над $ mathbb R_ $ или над $ mathbb C_ $. Сама теорема существования собственного числа гарантирует нам только лишь наличие этих чисел в поле $ mathbb C_ $. Как следствие, даже если рассматриваются операторы над полем $ mathbb R_ $ (что чаще всего и случается на практике), то существование для них вещественного канонического базиса вовсе не гарантировано.

Задача. Найти условия диагонализуемости матрицы оператора $ mathcal A $ над полем вещественных чисел.

Необходимое условие следует из теоремы $ 2 $ предыдущего пункта: все собственные числа матрицы должны быть вещественными.

Теорема $ 3 $ позволяет сформулировать и достаточный критерий диагонализуемости матрицы оператора $ mathcal A $ над $ mathbb R_ $.

Теорема. Если характеристический полином оператора имеет только простые вещественные корни, то матрица оператора диагонализуема над $ mathbb R_ $.

Условие различности и вещественности корней произвольного полинома $ f(lambda)=lambda^n+a_1lambda^+dots+ a_n in mathbb R[x] $ можно проверить по коэффициентам этого полинома «чисто алгебраически», т.е. за конечное число элементарных алгебраических операций над этими коэффициентами. Воспользуемся, например, теоремой Якоби из раздела ☞ ЛОКАЛИЗАЦИЯ КОРНЕЙ ПОЛИНОМА. По коэффициентам $ a_1,dots,a_n $ можно определить сумму Ньютона полинома $ f(lambda) $, т.е. величину $$ s_k=sum_ lambda_j^k . $$ Далее, после нахождения всех этих сумм для значений $ k in $, из них составляется ганкелева матрица $$ S=left[ s_ right]_^ $$ и вычисляются ее главные миноры $ S_1,dots, S_ $. Для различности всех корней полинома необходимо и достаточно выполнение условия $ S_n ne 0 $ (этот минор совпадает с дискриминантом $ mathcal D(f) $ полинома $ f(lambda) $); для различности и вещественности всех корней необходимо и достаточно, чтобы были выполнены неравенства $$ S_1ge 0,dots,S_ ge 0,S_n > 0 . $$

Пример. Найти все вещественные значения параметра $ <color > $, при которых матрица

$$ left( begin 1 &2, <color > & <color > -2 \ -1 &2 &1 \ 2 & 0 & -3 end right) $$ диагонализуема над $ mathbb R_ $.

Решение. На основании теоремы нам нужно установить условия вещественности корней характеристического полинома $ f(lambda)=-lambda^3+3, lambda-2,(3, <color > -1) $. Вычисляем суммы Ньютона: $ s_0=3, s_1= 0, s_2=6, s_3=18, <color > -6, s_4=18 $, составляем матрицу: $$ S=left(begin 3 & 0 & 6 \ 0 & 6 & 18, <color > -6 \ 6 & 18, <color > -6 & 18 end right) $$ и вычисляем ее главные миноры: $$S_1=3, S_2=18, S_3=-324, <color > , (3, <color > -2)=mathcal D(f) . $$ При $ <color > ne 0 $ и $ <color > ne 2/3 $ все собственные числа различны, условие теоремы выполняется при $ <color > in ]0,, 2/3[ $. Граничные точки последнего интервала следовало бы исследовать отдельно: хотя этим значениям параметра и соответствует случай кратных вещественных корней характеристического полинома, но матрица $ A_ $ может оказаться диагонализуемой на основании теоремы 5 предыдущего пункта. Но при решении примера в предыдущем пункте мы уже установили, что это условие не выполняется.

Ответ. Матрица диагонализуема над $ mathbb R_ $ при $ <color > in ]0,, 2/3[ $.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Жорданова нормальная форма

Если матрица оператора оказывается недиагонализуемой над $ mathbb C_ $, то к какому простейшему виду ее можно привести ? — Этим видом является, например, ☞ ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА.

Видео:Векторы в координатной плоскости.Скачать

Задачи

Видео:§35 Формулы поворота координатных осейСкачать

Источники

[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.

[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960

[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Скалярное произведение в разработке игр: проекции и прыгающие мячики в Unity ⛹

Видео:§11 Ориентация векторов в пространствеСкачать

furry.cat

Скалярное произведение – простой, но чрезвычайно полезный математический инструмент. Он кодирует отношение между величинами и направлениями двух векторов в единственное скалярное значение. Его можно использовать для вычисления проекции, отражения, расчета тени и постановки освещения. Из этого руководства вы узнаете:

• Геометрический смысл скалярного произведения.
• Как спроецировать один вектор на другой.
• Как измерить размер объекта вдоль произвольной оси.

• Как отразить вектор относительно плоскости.
• Как создать эффект отскока мяча от наклонной поверхности.

Видео:Векторы на плоскостиСкачать

Скалярное произведение

Представьте два вектора a и b . Вектор характеризуется только направлением и величиной (длиной), поэтому не имеет значения, в каком месте плоскости он расположен. Допустим, оба вектора начинаются в одной точке:

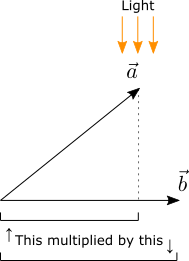
a и b , выходящие из одной точки плоскости» data-src=»https://media.proglib.io/posts/2020/04/04/182e211c01704ab48d14f469d9838df4.png» > Два вектора a и b , выходящие из одной точки плоскости

Проекцию одного вектора на другой можно представить как отбрасывание тени от первого вектора в направлении, перпендикулярном второму:

Проекция одного вектора на другой

Как вы знаете, операция вычисления произведения векторов записывается так:

Далее в статье мы будем использоваться запись a * b .

Если между векторами острый угол, то длина проекции будет положительной величиной, если больше – то отрицательной.

Если b – единичный вектор, то величина проекции a на b – это просто произведение a * b .

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Вычисление скалярного произведения через косинус угла

На схеме изображен прямоугольный треугольник. Угол между векторами a и b равен θ .

Два вектора образуют прямоугольный треугольник

Для начала требуется рассчитать величину проекции вектора a на вектор b – это нижний катет в нарисованном нами треугольнике. Длину катета стороны можно найти, умножив длину гипотенузы треугольника на косинус прилежащего угла.

a на вектор b – это катет прямоугольного треугольника» data-src=»https://media.proglib.io/posts/2020/04/04/c4a332573e7bdc88dcc72dddf457044d.png» > Проекция вектора a на вектор b – это катет прямоугольного треугольника

Итак, длина проекции равна произведению модуля вектора a на косинус угла θ . Скалярное произведение можно выразить следующим образом:

Формула вычисления скалярного произведения через косинус

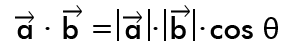
Эта формула лишний раз подтверждает, что порядок умножения не важен – в результат входят беззнаковые длины обоих векторов. Если оба вектора – единичные, правая часть формулы упрощается до cos(θ) . А если угол равен 90° (векторы перпендикулярны), то их произведение равно 0 .

Если угол острый (меньше 90°), результат будет положительным, так как косинус такого угла больше 0. Аналогично для тупого угла получится отрицательный результат. Таким образом, знак скалярного произведения дает нам некоторое представление о направлениях векторов.

Функция косинуса монотонно убывает на промежутке от 0 до 180° (от 1 до -1 ). Следовательно, чем ближе направления двух векторов, тем больше их скалярное произведение и наоборот.

• Направления совпадают, угол θ равен 0°, произведение равно |a| * |b| .
• Направления противоположны, угол θ равен 180°, произведение – -1* |a| * |b| .

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Вычисление скалярного произведения через компоненты векторов

Если наши векторы расположены в 3D-пространстве и имеют по три координаты каждый, не совсем понятно, где тот угол, косинус которого нужно вычислить. К счастью, существует другой способ расчета скалярного произведения – без всякой тригонометрии! Для начала нужно разложить каждый вектор на компоненты:

Разложение векторов на компоненты

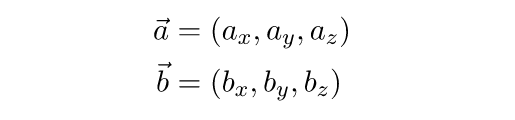
Намного проще и без всяких косинусов! В Unity есть встроенный метод Vector3.Dot для вычисления скалярного произведения двух векторов:

Его реализация выглядит следующим образом:

Нам известно, как найти длину вектора по его координатам:

Но ее можно выразить и через скалярное произведение вектора на себя:

Вернемся к формуле a * b = |a| * |b| * cos θ . При известных длинах векторов мы можем вычислить угол между ними с помощью функции арккосинуса:

Вычисление величины угла между векторами

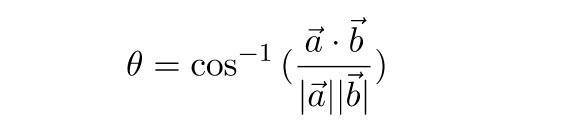
Если оба вектора являются единичными, мы можем упростить формулы:

Упрощенные формулы для единичных векторов

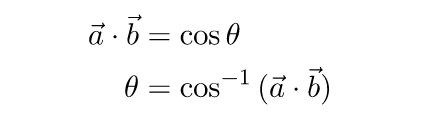
Видео:№743. Начертите ненулевой вектор a и отметьте на плоскости три точки A, B, C.Скачать

Проекция вектора

Теперь, когда нам известно геометрическое значение скалярного произведения векторов (произведение длины со знаком первого проецируемого вектора и длины второго вектора), мы можем перейти к практическому применению этого знания. Например, спроецируем один вектор на другой.

Пусть вектор с = project ba – это проекция вектора a на вектор b .

Вектор c – проекция вектора a на вектор b

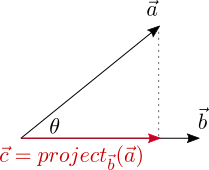
Возьмем единичный вектор в направлении вектора b . Он будет равен b / |b| . Если мы возьмем величину проекции a на b со знаком и умножим на этот единичный вектор, то получим вектор c . Cкалярное произведение a * b – это результат умножения длины b на длину проекции a на b . Отсюда получаем, что длину c со знаком можно найти, разделив скалярное произведение a * b на длину b :

Вычисление длины проекции одного вектора на другой

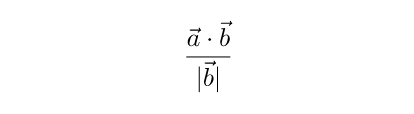
Умножив полученное значение на единичный вектор b / |b| , получаем формулу для нахождения проекции вектора:

Вычисление проекции одного вектора на другой

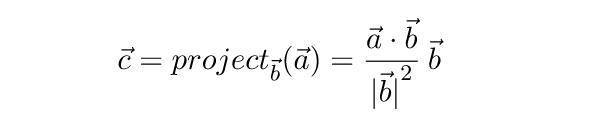
Вспомним теперь, что квадрат длины вектора равен его скалярному произведению на самого себя, и перепишем формулу:

Вычисление проекции одного вектора на другой

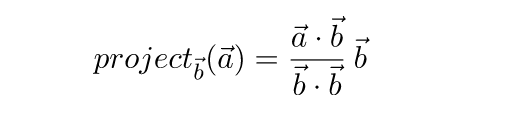
Если b – единичный вектор, то можно упростить еще больше:

Вычисление проекции вектора на единичный вектор

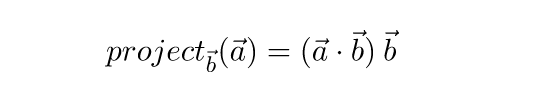
В Unity для вычисления проекции одного вектора на другой есть специальная функция Vector3.Project :

Вот так выглядит ее реализация:

Следует остерегаться возможного вырожденного случая, когда вектор, на который происходит проекция, – нулевой или имеет малую величину. При этом произойдет численный «взрыв» из-за деления на 0 или близкое к нему значение. Один из способов решить проблему – заранее вычислять величину вектора и при необходимости использовать резервный вариант (единичный вектор).

Видео:Как разложить вектор по базису - bezbotvyСкачать

Упраженение #1. Линейка

В качестве упражнения для закрепления знаний о векторной проекции сделаем линейку, которая измеряет размер объекта вдоль произвольной оси.

Линейка характеризуется базовой позицией (точка) и осью (единичный вектор):

Как спроецировать какую-либо точку ( Point ) на линейку? Прежде всего, найдем относительный вектор от базовой позиции линейки ( Base ) до этой точки. Затем спроецируем его на ось линейки ( Axis ). Проекция точки ( Projection ) – это базовое положение линейки, смещенное на проекцию относительного вектора.

Проекция точки на линейку

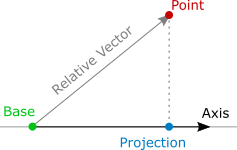
Промежуточное значение relativeDot в коде отражает, насколько далеко проекция точки находится от базового положения линейки – в направлении оси линейки, если она положительная, или в противоположном направлении, если отрицательная.

Чтобы найти размер объекта вдоль оси линейки, нужно провести такие измерения для каждой вершины меша (Mesh) и найти минимальное и максимальное значение. Ответ будет равен разнице между ними.

Видео:Геометрия 10 класс (Урок№17 - Вектор в пространстве.)Скачать

Отражение вектора

Еще одно практическое применение скалярного произведения – отражение вектора относительно плоскости. Рассмотрим вектор v и плоскость с нормальным вектором (перпендикуляром) n .

Отражение вектора v от плоскости

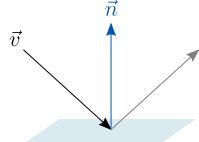
Мы можем разложить отражаемый вектор на параллельную и перпендикулярную к плоскости составляющие:

Разложение отражаемого вектора на составляющие

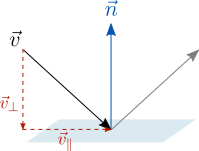
Сам вектор является суммой параллельной и перпендикулярной составляющих:

Разложение отражаемого вектора на составляющие

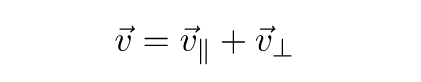
Перпендикулярный компонент, как вы уже догадались – это проекция вектор на нормаль плоскости. Параллельный компонент можно получить вычитанием этой проекции из самого вектора:

Получение параллельного плоскости компонента вектора

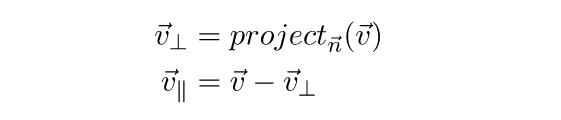
Теперь, чтобы получить искомый отраженный вектор, нужно перевернуть перпендикулярную составляющую и прибавить ее к параллельной:

Получение отраженного от плоскости вектора

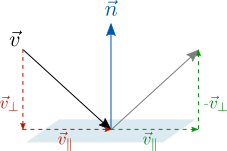
Параллельный компонент можно заменить разностью самого вектора и перпендикулярной составляющей, тогда получим следующий вид формулы:

То есть разность самого вектора и его удвоенной проекции на нормаль плоскости.

В Unity, конечно же, есть встроенная функция для расчета отраженного вектора – Vector3.Reflect :

Так выглядит реализация согласно первой выведенной нами формуле:

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Упражнение #2. Отскок мяча от наклонной плоскости

Теперь, когда мы знаем все об отражении вектора от плоскости, можно переходить на следующий уровень сложности. Попробуем сымитировать движение мяча, отскакивающего от склона.

Для моделирования траектории движения шара под действием силы тяжести мы будем использовать метод Эйлера.

Чтобы определить, когда мяч ударяется о склон, нужно как-то определить момент, когда мяч проникает в плоскость.

Сфера может быть определена центром ( C ) и радиусом ( R ). Плоскость определяется нормальным вектором ( n ) и точкой на плоскости ( P ). Вектор от P до С обозначим u .

Сфера и плоскость

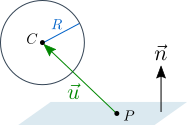
Если сфера НЕ проникает в плоскость, перпендикулярный плоскости компонент вектора u , должен иметь то же направление, что и вектор n , а также длину не менее R .

Перпендикулярный плоскости компонент вектора

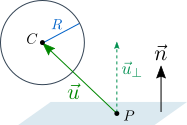
Другими словами, сфера не проникает в плоскость, если скалярное произведение векторов u и n больше R . В противном случае величина проникновения составляет R – u * n , и положение сферы нужно исправить.

Чтобы это сделать, можно просто переместить сферу в направлении нормали плоскости n на величину проникновения. Это лишь приближенное решение, которое не является физически правильным, но для упражнения оно хорошо подходит.

Добавим логику для коррекции позиции:

Нам также нужно отразить скорость, с которой движется сфера, относительно наклона, чтобы она правильно отскакивала.

Эта анимация демонстрирует идеальное отражение и выглядит неестественной. Мы ожидаем, что с каждым отскоком скорость мяча будет уменьшаться.

Это поведение обычно моделируется значением реституции (восстановления) между двумя сталкивающимися объектами. При 100% реституции мяч идеально отскакивает от плоскости. При 50% – величина перпендикулярной к плоскости составляющей скорости мяча будет уменьшена вдвое.

Величина реституции – это отношение величин перпендикулярного к плоскости компонента скорости мяча до и после отскока.

Вот пересмотренный с учетом коэффициента восстановления скорости вариант функции отражения:

Вот так выглядит обновленная функция SphereVsPlane :

Логика корректировки позиции заменяется логикой полноценного отскока:

Теперь мы можем устанавливать разные коэффициенты реституции для разных шариков:

Видео:7. Теорема Шаля. Богатство движений плоскостиСкачать

Заключение

Мы ответили на все вопросы, заданные в начале этого руководства.

• Скалярное произведение двух векторов – это произведение проекции первого вектора на второй (с учетом знака) и модуля второго вектора.
• Существует две формулы вычисления скалярного произведения: через косинус угла и через компоненты векторов.
• Скалярное произведение имеет множество полезных практических применений. Например, оно позволяет рассчитать проекцию вектора на другой вектор.
• С помощью скалярного произведения можно найти отраженный от плоскости вектор. На этой основе строятся различные физические модели, например, имитация отскока шарика от плоскости.

Расскажите в комментариях – разрабатываете ли вы сейчас какую-нибудь игру и если да, то о чем она. Каких уроков по Unity вам не хватает?

Двумерные преобразования

ТЕМА 2. ДВУМЕРНЫЕ ПРЕОБРАЗОВАНИЯ

2.1. Общие замечания

В компьютерной графике, наряду с соответствующими алгоритмами рисования, важно иметь математический аппарат, позволяющий редактировать изображение, т. е. осуществлять его преобразование (модификацию) в соответствии с требованиями решаемой задачи. Необходимо уметь производить с графическими объектами (точками, отрезками прямых, плоскими и объемными фигурами) такие операции, как масштабирование (в том числе пропорциональное), сдвиги, симметричные отражения (относительно точки, линии, плоскости), повороты (например, относительно какой-либо точки или линии), перемещения и т. п. Подобные действия и их комбинации обычно реализуются с помощью матричных операций с данными. Краткие сведения об основах матричных преобразований, используемых при формировании двумерных сцен, приведены ниже (в рамках данной темы). Аналогичные преобразования при формировании объемных сцен кратко рассмотрены в следующей теме.

2.2. Простые преобразования точек

Точка P на плоскости однозначно определяется двумя своими координатами (x, y). В соответствие ей можно поставить матрицу-строку размером 1´2 вида (сначала будем использовать именно такое отображение точки). Следует заметить также, что точка может задаваться и соответствующей матрицей-столбцом размером 2´1. В любом случае матрицу, определяющую положение точки, часто называют координатным вектором или вектором положения.

Большинство из перечисленных выше элементарных преобразований по отношению к точке можно реализовать путем умножения матрицы на матрицу общего преобразования размером 2´2 вида :

,

где , – координаты точки P*, являющейся результатом преобразования точки P, причем .

Рассмотрим некоторые специальные случаи.

Умножение исходной матрицы на единичную 2´2 матрицу (a = d = 1, b = c = 0)

не приводит к каким-либо изменениям; поэтому подобную единичную матрицу часто называют матрицей тождественного преобразования.

– происходит так называемое локальное масштабирование (растяжение при |a| > 1 или сжатие при 0 1 или сжатие при 0 0 происходит отражение относительно оси y, при a > 0, d 1, происходит равномерное расширение, т. е. увеличение исходной фигуры, если же 0 0 осуществляет непропорциональное локальное масштабирование; неравномерное расширение и сжатие возникают в зависимости от значений (в рассматриваемом случае – положительных) a и d, которые могут быть больше или меньше, чем 1, независимо друг от друга.

2.7. Комбинированные преобразования

При модификации графического объекта часто требуется не одно простое его преобразование, а несколько последовательно проведенных преобразований. В этом случае исходную матрицу (составленную из координат точки, концов отрезка или вершин многоугольника) можно умножить на матрицу первого преобразования, полученный результат – на матрицу второго преобразования и т. д. Конечный результат будет определяться выражением

,

где – матрица n-го преобразования, n = 1, 2, …, N.

При подобных действиях следует учитывать то обстоятельство, что операция умножения матриц не является коммутативной (т. е. в общем случае ), и следует строго соблюдать порядок (последовательность) выполнения преобразований (операций умножения).

Вместе с тем, для матриц справедлив ассоциативный закон: . Поэтому для достижения того же результата можно поступить иначе: отдельные преобразования предварительно комбинировать, т. е. рассчитать матрицу полного преобразования (такую матрицу называют также композицией преобразований), и затем применить ее для преобразования исходной матрицы –

.

Продемонстрируем оба возможных подхода к комбинированному преобразованию на простом примере. Пусть требуется исходную фигуру – например, треугольник F (рис.2.8), координаты вершин которого сведены в 3´2 матрицу – повернуть на 90° вокруг точки начала координат и затем полученную промежуточную фигуру симметрично отразить относительно прямой у = – x. Первому преобразованию соответствует матрица , а второму – матрица . Осуществим последовательно соответствующие умножения:

;

очевидно, что первое умножение приводит к промежуточному результату – треугольнику F¢ (рис.2.8), второе – к конечному результату – треугольнику F* (рис.2.8).

Используем другой возможный путь комбинированного преобразования: рассчитаем матрицу полного преобразования

и умножим на нее исходную матрицу

;

результат – треугольник F* (рис.2.8) – в точности совпадает с предыдущим.

Отметим здесь, что приведенный пример очень прост: выполняются два тривиальных преобразования, результат которых можно было бы получить с помощью единственного отражения (относительно оси y). Однако он иллюстрирует изложенные выше общие положения, связанные с комбинированными преобразованиями. Далее мы будем иметь возможность познакомиться с более сложными вариантами таких преобразований.

2.8. Однородные координаты

Ранее было замечено, что использование двумерных координатных векторов, отображающих точки на плоскости, в совокупности с матрицей общего преобразования размером 2´2 накладывает ряд ограничений на модификацию объектов. В первую очередь, эти ограничения обусловлены невозможностью применения преобразования координат. Существенно расширить возможности модификации позволяет использование однородных координат для отображения точек и, соответственно, матрицы общего преобразования размером 3´3.

Однородные координаты точки P (x, y) на физической плоскости xy представляют собой тройку чисел x¢, y¢, h; первые два из них связаны с реальными координатами точки соотношениями x¢ = hx и y¢ = hy, а h – это некоторое вещественное число (отметим, что случай h = 0 является особым и будет рассмотрен ниже). Однородным координатам точки можно поставить в соответствие трехмерный координатный вектор (вектор положения) – матрицу размером 1´3 вида . Очевидно, что при таком подходе каждую точку можно связать с бесконечным множеством наборов однородных координат и, соответственно, координатных векторов вида . Вместе с тем, для точки имеется лишь один набор однородных координат со значением h = 1; ему соответствует вектор положения вида . В компьютерной графике для отображения точек (за исключением точек бесконечности, см. далее) используются координатные векторы именно такого вида.

Применяя к вектору положения исходной точки матрицу общего преобразования размером 3´3 вида , получаем:

.

Данный результат практически идентичен тому, который был получен при умножении координатного вектора на матрицу общего преобразования размером 2´2 (см. выше). Выражения для координат и преобразованной точки в обоих случаях полностью совпадают. Следовательно, использование однородных координат совместно с матрицей общего преобразования вида позволяет осуществить все те преобразования точек, отрезков и многоугольников, о которых шла речь выше (это и происходит при реальной обработке графических объектов). Задавая соответствующие значения a, b, c и d, можно реализовать тождественное преобразование, операции локального масштабирования, отражения, сдвига и поворота, аналогичные уже рассмотренным. Однако, все они, по-прежнему, будут осуществляться относительно точки начала координат.

2.9. Перемещение

Исследуем теперь дополнительные возможности, открывающиеся при новом подходе к преобразованиям. Проведем следующую матричную операцию:

;

полученный результат можно трактовать двояко: с одной стороны, можно считать, что операция привела к перемещению исходной точки вдоль осей x и y соответственно на m и n в исходной системе координат x0y (рис.2.9а); с другой стороны, можно полагать, что точка осталась на месте, а произошло преобразование координат – новая система координат x*0*y* сдвинута относительно исходной на – m вдоль оси x и на – n вдоль оси y (рис.2.9б).

В любом случае, выяснилось, что элементы m и n матрицы преобразования размером 3´3 являются коэффициентами перемещения в направлениях x и y соответственно. И не менее важный вывод из приведенного примера – теперь каждая точка плоскости, в том числе начало координат, может быть преобразована.

2.10. Поворот вокруг произвольной точки

Имея более мощный, чем ранее, математический аппарат можно реализовать и такое преобразование. Последовательность действий при этом может быть следующей:

§ объект преобразования перемещается таким образом, чтобы точка, относительно которой совершается поворот, попала в начало координат;

§ выполняется поворот объекта на требуемый угол вокруг точки начала координат;

§ осуществляется обратное перемещение объекта так, чтобы точка центра вращения возвратилась на исходное место.

Применительно координатному вектору точки подобная операция поворота вокруг точки с координатами (m, n) на произвольный угол q реализуется следующими матричными преобразованиями:

;

комбинируя три матрицы преобразования, получаем

.

Приведем простой пример рассмотренной операции: поворот отрезка L (рис.2.10), заданного однородными координатами его концов и , на 90° в положительном направлении (против часовой стрелки) вокруг точки с координатами (4, 5 ). Обобщая предыдущее выражение на случай преобразования отрезка, запишем (после подстановок в матрицу преобразования конкретных значений и расчета входящих в нее коэффициентов)

;

результат преобразования – отрезок L* (рис.2.10).

2.11. Отражение относительно произвольной прямой

В разделе 2.5 обсуждались случаи отражения относительно ряда характерных прямых, проходящих через точку начала координат. Рассмотрим теперь более сложное преобразование – симметричное отражение объекта относительно произвольной прямой линии, причем не проходящей через начало координат. Используемый теперь подход позволяет достичь этого преобразованием, включающим пять последовательных операций:

§ перемещение объекта преобразования вдоль оси x или y таким образом, чтобы линия, относительно которой он отражается, прошла через начало координат;

§ поворот объекта относительно точки начала координат до совпадения линии, относительно которой он отражается, с одной из координатных осей;

§ симметричное отражение объекта относительно данной координатной оси;

§ обратный поворот объекта относительно точки начала координат (на тот же угол, что и во втором пункте, но в обратном направлении);

§ обратное перемещение объекта вдоль оси x или y (на то же расстояние, что и в первом пункте, но в обратном направлении).

В матричном виде полное преобразование, представляющее собой комбинацию пяти преобразований, можно записать так:

,

где – матрица перемещения, – матрица поворота вокруг начала координат, – матрица отражения относительно соответствующей координатной оси, и – матрицы, обратные матрицам соответственно и .

Приведем конкретный пример: симметричное отражение треугольника F (рис.2.11а), координатные векторы вершин которого представляются как , и , относительно прямой линии . Для того, чтобы линия прошла через точку начала координат, можно осуществить перемещение вдоль оси y на – 2 единицы; поворот относительно начала координат на – arctg 0,5 = – 26,57 ° приведет к тому, что линия совпадет с осью x; матрица отражения относительно оси x очевидна; обратный поворот и обратное перемещение осуществляются матрицами, обратными матрицам второго и первого преобразований. Композиция преобразований будет иметь вид:

;

реализуя полное преобразование, получим:

;

рис.2.11б, в, г, д иллюстрируют различные этапы промежуточных преобразований в случае последовательного их применения к исходной матрице, а рис.2.11е – конечный результат (который, вообще говоря, получен одной матричной операцией после расчета матрицы полного преобразования) – треугольник F*.

2.12. Проецирование в однородных координатах

Матрицу общего преобразования для трехмерных координатных векторов, используемых при двумерных преобразованиях, в общем виде можно представить так:

.

Ранее было установлено, как входящие в нее коэффициенты a, b, c, d, m и n влияют на соответствующие преобразования. Остальным трем коэффициентам в предыдущих разделах присваивались вполне определенные значения ( p = q = 0, s = 1), и они, по сути дела, не принимали участия в преобразованиях. Координатные векторы преобразованных точек всегда имели вид , т. е. число h (см. раздел 2.8) тождественно принимало единичное значение. Геометрически это можно трактовать как ограничение преобразований физической плоскостью h = 1 в трехмерном пространстве xyh. Вместе с тем, при других значениях коэффициентов p, q и s они также могут участвовать в преобразованиях.

Рассмотрим сначала, к какому эффекту приведут ненулевые значения коэффициентов p и q. Запишем следующее выражение:

;

данное преобразование привело к тому, что точка (x, y), которой изначально ставился в соответствие координатный вектор вида , преобразована в точку, которой ставится в соответствие координатный вектор вида , где x¢ = x, y¢ = y, ; с геометрической точки зрения полученный результат интерпретируется следующим образом: в трехмерном пространстве xyh конец P (рис.2.12) координатного вектора исходной точки принадлежит плоскости h = 1, а конец P¢ координатного вектора преобразованной точки – плоскости (причем в данном конкретном случае две другие компоненты однородных координат и соответствующего координатного вектора остаются неизменными).

Однако, как отмечалось ранее, в компьютерной графике используют векторы положения только вида . Поэтому, когда какое-либо преобразование приводит к результату с h ≠ 1 (и, кстати, с h ≠ 0), этот результат нормализуют, т. е. приводят к требуемому виду путем деления всех трех составляющих однородных координат на величину h. В рассматриваемой задаче окончательный результат преобразования будет иметь вид

;

геометрически такой же результат, а именно точку P* (рис.2.12), можно получить путем проецирования точки P¢, принадлежащей плоскости h ≠ 1, на плоскость h = 1 по лучу, соединяющему точку P¢ с началом координат.

Нетрудно заметить, что при h > 1 (как на рис.2.12) координаты x* и y* преобразованной точки пропорционально уменьшаются (в h раз) по сравнению теми же координатами исходной точки; при h 1 имеет место равномерное расширение, при 0 1 – равномерное сжатие, если 0 0, на положительной полуоси x, при условии, что x 0 положительной полуоси y, при y 0 – в первом квадранте координатной плоскости xy, при x = y 0, y 0 – во втором ее квадранте.