Отношения отрезков при параллельных прямых (4 видео)

Теорема Фалеса: формулировка и пример решения задачи

В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.

Содержание

Формулировка теоремы
Обобщенная формулировка
Обратная теорема Фалеса
Пример задачи
Математика
Теоремы о пропорциональных отрезках
Теорема Фалеса
Формулировка теоремы Фалеса
Примеры решения задач
Историческая справка
💡 Видео

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Формулировка теоремы

Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.

Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.

Обобщенная формулировка

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.

В соответствии с этим для нашего чертежа выше справедливо следующее равенство:

* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.

Обратная теорема Фалеса

1. Для пересекающихся секущих

Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.

Из обратной теоремы следует:

Обязательное условие: равные отрезки должны начинаться от вершины.

2. Для параллельных секущих

Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.

Видео:Отношение длин отрезковСкачать

Пример задачи

Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.

Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.

Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Математика

Четыре отрезка называются пропорциональными, если они такой величины, что образуют пропорцию. В этом случае отношение двух отрезков по длине равно отношению других двух отрезков.

Так четыре отрезка AB, CD, EF, GH (черт. 144) будут пропорциональными, если они удовлетворяют пропорции:

В этой пропорции под отрезками AB, CD подразумевают их длины. Так как длина отрезков может быть выражена числом, которое выражает отношение длины отрезка к длине, принятой за единицу, то под отрезками AB, CD, EF, GH можно подразумевать и сами числа.

На этом основании пропорция из отрезков обладает всеми свойствами пропорции, составленной из чисел.

Члены пропорции можно переставлять, перемножать и т. д.

Таким образом из пропорции (1) вытекает равенство

а также пропорции:

AB/EF = CD/GH, GH/CD = EF/AB и т. д.

Каждый из отрезков по отношению к остальным называется четвертым пропорциональным .

Таким образом отрезок GH будет четвертым пропорциональным отрезкам EF, CD, AB. Отрезок AB четвертым пропорциональным отрезкам CD, EF, GH.

Видео:Теорема о пропорциональных отрезкахСкачать

Теоремы о пропорциональных отрезках

В основу всех предположений о пропорциональных отрезках может быть положена следующая теорема.

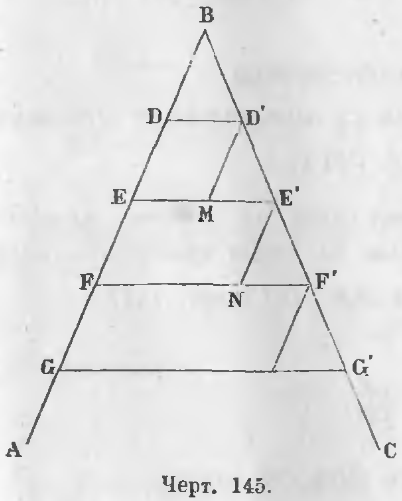
Теорема 83. Если от вершины угла по стороне его отложим несколько равных частей и проведем через точки деления параллельные прямые до другой стороны угла, на последней отложатся тоже равные части.

Дан угол ABC (черт. 145), на одной стороне которого отложены равные части BD, DE, EF, FG и проведены параллельные линии DD’, EE’, FF’, GG’, то есть

BD = DE = EF = FG
DD’ || EE’ || FF’ || GG’

Требуется доказать, что

Доказательство. Проведем отрезок D’M параллельно лучу AB. Треугольники BDD’ и D’ME’ равны, ибо D’M = BD (потому что D’M = DE как части параллельных между параллельными, а DE = BD по условию, следовательно, D’M = BD).

∠B = ∠MD’E’ (как соответствующие углы при пересечении параллельных прямых BD и D’M третьей прямой BC).

∠BDD’ = ∠D’ME’ (ибо ∠BDD’ = ∠BEE’, а ∠BEE’ = ∠D’ME’). Следовательно, BD’ = D’E’.

Подобным же образом, проведя отрезок E’N параллельно AB, можно доказать, что D’E’ = E’F’. Следовательно,

BD’ = D’E’ = E’F’ = … (ЧТД).

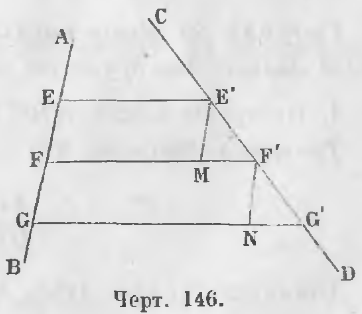
Теорема 84. Если на одной прямой отложим несколько равных частей и проведем параллельные прямые до пересечения с другой прямой, на последней отложатся тоже равные части.

Дано. На прямой AB отложены равные части EF, FG и проведены параллельные прямые EE’, FF’, GG’ (черт. 146).

Требуется доказать, что E’F’ = F’G’ и т. д.

Доказательство. Проведем отрезки E’M, F’N параллельно прямой AB, тогда треугольники E’MF’ и F’NG’ равны, ибо E’M = F’N (E’M = EF, F’N = FG и так как EF = FG, то E’M = F’N).

∠ME’F’ = ∠NF’G’ как соответственные.

∠E’MF’ = ∠F’NG’ как углы с параллельными сторонами.

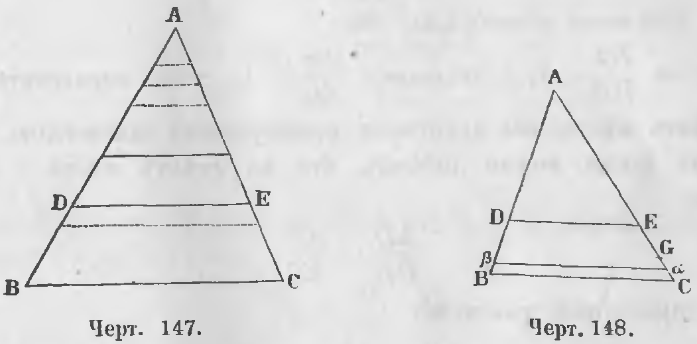
Теорема 85. Прямая, параллельная одной из сторон треугольника, делит две другие его стороны на части пропорциональные.

Дано. В треугольнике ABC прямая DE || BC (черт. 147).

Требуется доказать, что

Доказательство. Здесь могут быть два случая:

1) когда отрезки AD и DB соизмеримы и

2) когда они несоизмеримы.

Первый случай. Отрезки AD и DB соизмеримы. Положим, что их общая мера укладывается m раз в отрезке AD и n раз в отрезке DB. Разделив AD на m и DB на n равных частей и проведя из точек деления прямые, параллельные BC, мы разделим также и отрезок AE на m, а EC на n равных частей (теорема 83).

Рядом с отношением

имеет место отношение

Второй случай . Отрезки AD и DB несоизмеримы (черт. 148).

Докажем, что в этом случае не имеет мета ни неравенство

Чтобы имело место равенство, нужно второе отношение увеличить. Для этого нужно знаменатель этого отношения уменьшить, т. е. EC заменить меньшим отрезком EG. Тогда будет иметь место пропорция

Разделим отрезок AE на равные части, которые были бы меньше GC, и станем их откладывать от точки A по отрезку AC; тогда одна из частей упадет в точку α между G и C. Проведем из точки α прямую αβ параллельную BC, тогда отрезок AE будет соизмерим с E α и будет иметь место пропорция

Разделив отношение (1) на (2), получим равенство

Это равенство несообразно, ибо отношение D β /DB α /EG > 1, следовательно, неравенство (a) не имеет места, ибо ведет к несообразному заключению.

Точно также можно доказать, что не имеет места и неравенство

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Теорема Фалеса

Видео:24. Определение параллельных прямыхСкачать

Формулировка теоремы Фалеса

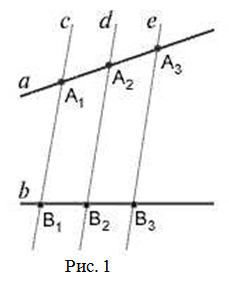
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

Обобщённая теорема Фалеса

Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема Фалеса

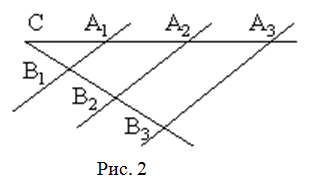
Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).

Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.

Видео:Отношение отрезковСкачать

Примеры решения задач

Задание. Разделить данный отрезок на четыре равные части.

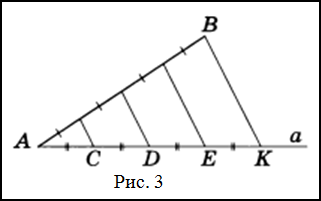
Решение. Пусть $AB$ — заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.

Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .

Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .

Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.

Теорема Фалеса не по зубам? Тебе ответит эксперт через 10 минут!

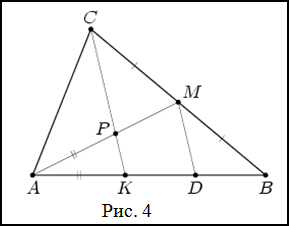
Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .

Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).

По теореме Фалеса $BD = KD$ .

По теореме о пропорциональных отрезках имеем, что

$$P M=K D=frac Rightarrow B K: P M=2: 1$$

Ответ. $B K: P M=2: 1$

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Историческая справка

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.

Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.