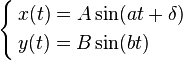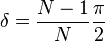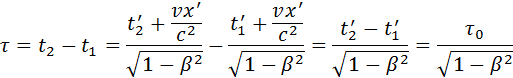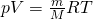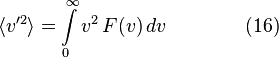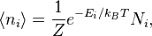| |
|
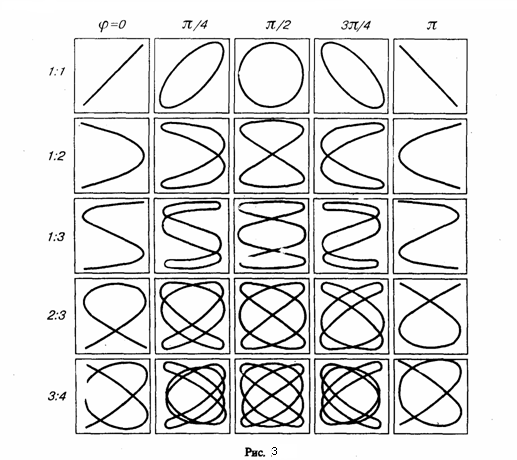
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 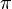
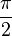
Математическое выражение для кривой Лиссажу[править | править вики-текст]
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности(A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышёва первого рода степени N.
| | | следующая лекция ==> | |
| Метод векторных диаграмм. Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А | | | Неинерциальные системы отсчета. Описание движения в неинерциальных системах. Силы инерции. Центробежная сила. Сила Кориолиса. |
Дата добавления: 2016-01-29 ; просмотров: 9406 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Сложение взаимно перпендикулярных гармонических колебанийСкачать

Сложение взаимно перпендикулярных колебаний
Если точка участвует одновременно в двух взаимно перпендикулярных колебаниях вдоль взаимно перпендикулярных осей р и то ее результирующее движение происходит по замкнутой криволинейной траектории. Такие траектории выписывает, например, электронный луч на экране осциллографа, если отклоняющая система вызывает его гармонические колебания в двух взаимно перпендикулярных направлениях (по оси Ох и Оу одновременно). С математической точки зрения можно считать уравнения складываемых колебаний параметрическим заданием траектории, а явный вид этой траектории можно получить, исключая время t из данных уравнений.
Наиболее простое уравнение траектории получится при сложении колебаний одинаковой частоты
Если обозначить разность фаз колебаний ф2 —
= Дф, то для дальнейшего анализа систему (2.31) можно переписать:
Чтобы получить уравнение траектории, нужно исключить из этих уравнений время t как параметр. Для этого из выражения (2.32) найдем cos(o)/) = с/А и тогда sin(a> = -^1 — /Д 2 . В выражении (2.33)
cos(cot + Дф) представим как cos(m/) cos Дф — sin(cof) sin Дф. Тогда его можно переписать в виде ц/А2 = cos((»/) cos Дф — sin(co?) sin Дф. В полученное выражение подставим значения cos(co?) и sin(co/) и получим
Перепишем его следующим образом
Возведем обе части этого равенства в квадрат
Это уравнение — уравнение эллипса, оси которого в общем случае не совпадают с осями ^ и г|.
Рассмотрим некоторые частные случаи.
1. Разность фаз Дф складываемых колебаний равна нулю или п. Тогда уравнение (2.38) запишется в виде:
это уравнение прямой с угловым коэффициентом ±АХ/А2, т.е.
Таким образом, эллипс при равной нулю (или л) разности фаз колебаний вырождается в прямую, проходящую через начало координат (на рис. 2.10, а приведены прямые р = +? для случая, когда А = Л2). Уравнение r(t) результирующего колебания (вдоль этой прямой) можно представить следующим образом:
что при равенстве амплитуд А1=А2 = А дает r(t) = A cos со А
2. Если разность фаз складываемых колебаний составляет п/2, то уравнение (2.38) переходит в каноническое уравнение эллипса
отнесенное к осям координат Юц (рис. 2.10, б). При=А2 эллипс вырождается в окружность.
Рис. 2.10. Сложение взаимно перпендикулярных колебаний: а — Дф = 0, г| = ^ (или при Аф = л, —г) = %) при А = Л2; 6 — Дф = л/2 при А > А2
Если частоты складываемых колебаний различаются, то на плоскости рOS, возникают сложные фигуры. Если частоты кратны друг другу, образуются так называемые фигуры Лиссажу, число самопересечений которых оказывается равным отношению складываемых частот колебаний.
Видео:Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать

Сложение взаимно перпендикулярных колебаний
Сложение двух колебаний в случае, когда они перпендикулярны друг другу, не всегда приводит к колебательному движению. Чаще реализуются случаи, когда тело в результате сложения перпендикулярных колебаний движется по какой-либо кривой. Этой кривой может быть эллипс, окружность, парабола и другие не столь простые геометрические фигуры. Случается, что наложение двух перпендикулярных колебаний приводит и к движению по прямой, т.е. колебательному движению, но в ином направлении, нежели направления складываемых колебаний. Зная их параметры, можно рассчитать траекторию результирующего движения, освободившись от времени t и, следовательно, от тригонометрических функций.
Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.
24. Процесс распространения колебаний в пространстве называется волной.
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
Звуковые волны– это механические волны с частотой колебаний примерно от 16 до 20000 Гц.
25. При распространении волн изменения их амплитуды и скорости в пространстве и появление дополнительных гармоник зависят от свойств анизотропности среды, сквозь которую проходят волны, границ, а также характера излучения источников волн.
Волновой фронт — это поверхность, до которой дошли колебания к данному моменту времени. Волновой фронт является частным случаем волновой поверхности.
Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Если источником волны является точка, то волновые поверхности в однородном и изотропном пространстве представляют собой концентрические сферы.
Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.
Уравнение плоской бегущей волны:
Длина волны — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
26. Гидростатическое давление – давление, оказываемое столбом жидкости или газа.
Закон Архимеда: на тело, погруженное в жидкость (или газ) действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости, вытесненной телом.
Закон Паскаля гласит, что давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.
27. Идеальная жидкость — это абстрактная жидкость, не обладающая вязкостью, теплопроводностью, способностью к электризации и намагничиванию.
Уравнение неразрывности струи.
Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Следовательно, объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·u·dt, то выполняется соотношение:
S1·u1 = S2·u2 или
S·u = const.
Конечное уравнение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.
Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде
где a(x) и b(x) − непрерывные функции.
28. Вязкостью жидкостей и газов называется их свойство оказывать сопротивление перемещению одних слоев относительно других.
Вязкость обусловлена возникновением сил внутреннего трения между слоями движущихся жидкостей и газов. Эти силы направлены по касательной к поверхности слоев, они тормозят более быстрые слои и ускоряют медленные.
29.
Преобразова́ния Галиле́я — в классической механике (механике Ньютона) и нерелятивистской квантовой механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой [1] . Термин был предложен Филиппом Франком в 1909 году. [2] Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время» [3] ).
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.
Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, можно считать во многом определяющим структуру ньютоновской механики. Вместе же с такими дополнительными идеями, как симметрия пространства и принцип суперпозиции в том или ином виде (утверждающий эквивалентность взаимодействия многих тел в малый промежуток времени композиции воображаемых последовательных попарных взаимодействий этих тел), преобразования Галилея могут быть практически достаточным основанием для формулировки ньютоновской механики (вывода ее основных законов)
При́нцип относи́тельности— фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.
30. Постулаты Эйнштейна:
Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.
Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике), можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение ИСО.
Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника.
Принцип постоянства скорости света противоречит классической механике, а конкретно — закону сложения скоростей. При выводе последнего используется только принцип относительности Галилея и неявное допущение одинаковости времени во всех ИСО. Таким образом, из справедливости второго постулата следует, что время должно быть относительным — неодинаковым в разных ИСО. Необходимым образом отсюда следует и то, что «расстояния» также должны быть относительны. В самом деле, если свет проходит расстояние между двумя точками за некоторое время, а в другой системе — за другое время и притом с той же скоростью, то отсюда непосредственно следует, что и расстояние в этой системе должно отличаться.
Преобразования Лоренца — линейные преобразования векторного псевдоевклидова пространства, сохраняющие длины или, что эквивалентно, скалярное произведение векторов.
31. Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x’ системы K’ происходит процесс длительностью τ0 = t’2 – t’1 (собственное время), где t’1 и t’2 – показания часов в системе K’ в начале и конце процесса. Длительность τ этого процесса в системе K будет равна:
Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K’ вдоль оси x’ движется частица со скоростью 
С помощью операции дифференцирования из формул преобразований Лоренца можно найти:
32. Формула Релятивистского импульса:
34
Идеальный газ — это газ, молекулы которого можно рассматривать как материаль- ные точки, а их взаимодействие носит характер абсолютно упругого удара. (при низком р и высокой Т реальные газы приближаются к идеальным).
Состояние некоторой массы газа определяется тремя термодинамическими пара- метрами: р,V,T.
Моль (обозначение: моль, международное: mol) — единица измерения количества вещества. Соответствует количеству вещества, в котором содержится NA частиц (молекул, атомов, ионов, электронов или любых других тождественных структурных частиц). [1] NA это постоянная Авогадро, равная количеству атомов в 12 граммах нуклида углерода 12C. Таким образом количество частиц в одном моле любого вещества постоянно и равно числу Авогадро NA.
NA = 6,02214179(30)×1023 моль−1.
Иначе говоря, молем [2] называется количество вещества, масса которого, выраженная в граммах, численно равняется его молекулярной массе.
Число Авогадро NА — это число молекул, содержащихся в одном моле любого вещества. Молярная масса — масса одного моля.
Уравнение состояния идеального газа. Опытные газовые законы.
В МКТ используют идеализированную модель идеального газа.
Идеальный газ — это газ, молекулы которого можно рассматривать как материальные точки, а их взаимодействие носит характер абсолютно упругого удара. (при низком р и высокой Т реальные газы приближаются к идеальным).
Состояние некоторой массы газа определяется тремя термодинамическими пара- метрами: р,V,T.
УРАВНЕНИЕМ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.
PV / T = const, при m = const — уравнение Клапейрона
Для произвольной массы газа (т. е. в общем виде) это уравнение представляет собой УРАВНЕНИЕ МЕНДЕЛЕЕВА — КЛАПЕЙРОНА:
p*V = (m/M)*R*T,
или p*V = R*T (для 1 моля) ,
где р — давление; V — объём; m — масса; Т — абсолютная температура, К; m — масса газа, М — молярная масса газа; R =8,31 (Дж/(моль*К)
Изопроцессы
Макропараметры: давление, объем и температура описывают состояние газа. Если при неизменной массе газа один из параметров не изменяется, получим изопроцессы.
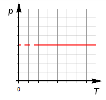
Графики изопроцессов демонстрируют как один макропараметр зависит от другого. Это обычные математические функциональные зависимости. Будем рассматривать зависимости p(T), V(T), p(V).




Изотермический процесс. 

Закон Бойля — Мариотта гласит:
При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно
В математической форме это утверждение записывается следующим образом
pV = const,
где p — давление газа; V — объём газа.
Важно уточнить, что в данном законе газ рассматриваеться как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молекулярная масса газа, тем больше это отличие.
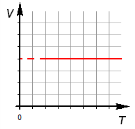
Закон Гей-Люссака — закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении
Закон Гей Люссака — при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре

Объем V данной массы газа при постоянном давлении газа прямо пропорционален изменению температуры
Закон Гей-Люссака справедлив только для идеальных газов, реальные газы подчиняются ему при температурах и давлениях, далеких от критических значений. Является частным случаем уравнения Клайперона.
Уравнение Менделеева Клапейрона :
Закон Шарля :
Закон Бойля Мариотта :
36.
Термодинамическая температура Т — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы“
закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν+dν, т. е.

откуда

Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:
Характерная скорость
Хотя Уравнение (11) дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.
Наиболее вероятная скорость
наиболее вероятная скорость, 



Подставляя 
Подставляя 
Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.
Согласно распределению Больцмана среднее число частиц с полной энергией 
где 





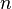
В случае, когда движение частиц подчиняется классической механике, энергию 
кинетической энергии 
внутренней энергии 
потенциальной энергии 
Обозначим 
Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», — при относительно высокой скорости теплового движения молекул (10 3 м/с) объясняется столкновениями молекул. Молекула газа время от времени сталкивается с другими молекулами. В момент столкновения молекула резко изменяет величину и направление скорости своего движения. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна:
 |
где 


Рис. 3.1
Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами (рис. 3.2).

Рис. 3.2


За одну секунду молекула проходит путь, равный средней арифметической скорости 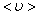
 | 3.2.1 |
Подсчитаем число столкновений ν.
Вероятность столкновения трех и более молекул бесконечно мала.
Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 3.3).
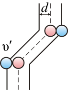
Рис. 3.2
Путь, который пройдет молекула за одну секунду, равен длине цилиндра 

 | 3.2.1 |
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга.
По закону сложения случайных величин
 | (3.2.1) |
А так как средняя длина свободного пробега 
 | (3.2.2) |
Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т.
Так как 

 | (3.2.3) |
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:
Диффузией называется самопроизвольное взаимное проникновение и перемещение молекул двух соприкасающихся газов, жидкостей или твердых тел. Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами,молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояниявещества. Теплопроводностьюназывается также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости. Способность вещества проводить тепло характеризуется коэффициентом теплопроводности (удельной теплопроводностью). Численно эта характеристика равна количеству теплоты, проходящей через образец материала толщиной в единицу длины (1 м), площадью в единицу площади (1 м 2 ), за единицу времени (1 секунду) при единичном температурном градиенте (1 К). В метрической системе мер единицей измерения коэффициента теплопроводности является Вт/(м·K). Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений второго порядка (таких, как уравнения Лагранжа) или половине числа уравнений первого порядка (таких, как канонические уравнения Гамильтона), полностью описывающих [1] динамику системы. Степени свободы молекулы Формула внутренней энергии идеального газа:  , и прямо связанная с ней формула для средней энергии молекулы идеального газа , и прямо связанная с ней формула для средней энергии молекулы идеального газа 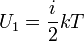 , где , где  — количество степеней свободы молекулы газа, — количество степеней свободы молекулы газа, 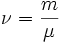 — количество газа ( — количество газа (  — масса, — масса,  — молярная масса газа), — молярная масса газа),  — универсальная газовая постоянная, — универсальная газовая постоянная,  — константа Больцмана, — константа Больцмана,  — абсолютная температура газа, — включают количество степеней свободы молекулы. Степени свободы молекулы вымораживаются, как это описано в параграфе выше, что означает, что эффективное i в формуле зависит от температуры и, вообще говоря, не может быть просто вычислено классическим механическим способом. Все вращательные степени свободы у одноатомных молекул и вращательная степень свободы, соответствующая вращению вокруг продольной оси у линейных (в реальном геометрическом смысле) молекул, выморожены (то есть не должны учитываться в i) всегда, поскольку их температуры вымораживания настолько высоки, что диссоциация молекул происходит гораздо раньше, чем эти температуры достигаются. В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы — абсолютная температура газа, — включают количество степеней свободы молекулы. Степени свободы молекулы вымораживаются, как это описано в параграфе выше, что означает, что эффективное i в формуле зависит от температуры и, вообще говоря, не может быть просто вычислено классическим механическим способом. Все вращательные степени свободы у одноатомных молекул и вращательная степень свободы, соответствующая вращению вокруг продольной оси у линейных (в реальном геометрическом смысле) молекул, выморожены (то есть не должны учитываться в i) всегда, поскольку их температуры вымораживания настолько высоки, что диссоциация молекул происходит гораздо раньше, чем эти температуры достигаются. В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы  где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул:  Внутренняя энергия для произвольной массы m газа. Внутренняя энергия для произвольной массы m газа.  где М — молярная масса, ν — количество вещества. работа А=p(v1-v2) где p — давление создаваемое поршнем= f/s где f-сила действующая на поршень s — площадь поршня примечание p=const v1 и v2 — начальные и конечные обьемы. Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние. Определение Рассмотрим систему, состоящую из двух тел A и B. Предположим, что тело B заключено почти полностью в жёсткую адиабатическую оболочку, так что оно не способно совершать макроскопическую работу, а обмениваться теплом (то есть энергией) посредством микроскопических процессов может лишь с телом A. Предположим, что тело A также заключено в адиабатическую оболочку почти полностью, так что для него возможен теплообмен лишь с B, но не будем предполагать, что оболочка жёсткая. Количеством теплоты, сообщённой телу A в некотором процессе, будем называть величину QA = − ΔUB, где ΔUB — изменение внутренней энергии тела B. Согласно закону сохранения энергии, ΔA = ΔUA + ΔUB где ΔA — макроскопическая работа внешних сил над телом A. Если учесть, что ΔA = − Aint где Aint — работа, совершённая телом A, то закону сохранения энергии можно придать форму первого начала термодинамики: ΔQA = ΔUA + Aint Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела B и способа теплообмена между телами. Заметим, что для определения количества теплоты необходимо пробное тело, в противном случае первое начало теряет смысл содержательного закона и превращается в определение количества теплоты (весьма бесполезное в таком виде) . При определении количества теплоты независимо от ΔA и ΔUA первое начало становится содержательным законом, допускающим экспериментальную проверку. Отметим, что, как и совершённая работа, количество переданной теплоты зависит от конкретного процесса, совершённого над телом. где М — молярная масса, ν — количество вещества. работа А=p(v1-v2) где p — давление создаваемое поршнем= f/s где f-сила действующая на поршень s — площадь поршня примечание p=const v1 и v2 — начальные и конечные обьемы. Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние. Определение Рассмотрим систему, состоящую из двух тел A и B. Предположим, что тело B заключено почти полностью в жёсткую адиабатическую оболочку, так что оно не способно совершать макроскопическую работу, а обмениваться теплом (то есть энергией) посредством микроскопических процессов может лишь с телом A. Предположим, что тело A также заключено в адиабатическую оболочку почти полностью, так что для него возможен теплообмен лишь с B, но не будем предполагать, что оболочка жёсткая. Количеством теплоты, сообщённой телу A в некотором процессе, будем называть величину QA = − ΔUB, где ΔUB — изменение внутренней энергии тела B. Согласно закону сохранения энергии, ΔA = ΔUA + ΔUB где ΔA — макроскопическая работа внешних сил над телом A. Если учесть, что ΔA = − Aint где Aint — работа, совершённая телом A, то закону сохранения энергии можно придать форму первого начала термодинамики: ΔQA = ΔUA + Aint Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела B и способа теплообмена между телами. Заметим, что для определения количества теплоты необходимо пробное тело, в противном случае первое начало теряет смысл содержательного закона и превращается в определение количества теплоты (весьма бесполезное в таком виде) . При определении количества теплоты независимо от ΔA и ΔUA первое начало становится содержательным законом, допускающим экспериментальную проверку. Отметим, что, как и совершённая работа, количество переданной теплоты зависит от конкретного процесса, совершённого над телом. |
Уде́льная теплоёмкость -отношение теплоёмкости к массе, теплоёмкость единичной массы вещества (разная для различных веществ); физическая величина, численно равная количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу. [1]
В Международной системе единиц (СИ) удельная теплоёмкость измеряется в джоулях на килограмм на кельвин, Дж/(кг·К) [2] . Иногда используются и внесистемные единицы: калория/(кг·К) и т.д.
Удельная теплоёмкость обычно обозначается буквами c или С, часто с индексами.
На значение удельной теплоёмкости влияет температура вещества и другие термодинамические параметры. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C. Кроме того, удельная теплоёмкость зависит от того, каким образом позволено изменяться термодинамическим параметрам вещества (давлению, объёму и т. д.); например, удельная теплоёмкость при постоянном давлении (CP) и при постоянном объёме (CV), вообще говоря, различны.
Формула расчёта удельной теплоёмкости: 
Молярная теплоёмкость — отношение теплоёмкости к количеству вещества, теплоёмкость одного моль вещества (в принципе разная для различных веществ, хотя в свете закона Дюлонга — Пти — имеет близкое значение, и даже приближенно совпадает в достаточно широких пределах изменения температуры у многих веществ).
Это физическая величина, численно равная количеству теплоты, которое необходимо передать одному молю (данного) вещества для того, чтобы его температура изменилась на единицу. [1]
В Международной системе единиц (СИ) молярная теплоёмкость измеряется в джоулях на моль на кельвин, Дж/(моль·К) [2] . Иногда используются и производные единицы, как Дж/(кмоль·К), или внесистемные единицы: калория/(кг·К) и т.д.
Молярная теплоёмкость обычно обозначается 

На значение молярной теплоёмкости влияет температура вещества и другие термодинамические параметры. К примеру, измерение молярной теплоёмкости воды даст разные результаты при 20 °C и 60 °C. Кроме того, удельная теплоёмкость зависит от того, каким образом позволено изменяться термодинамическим параметрам вещества (давлению, объёму и т. д.); например, удельная теплоёмкость при постоянном давлении (CP) и при постоянном объёме (CV), вообще говоря, различны.
Формула расчёта молярной теплоёмкости: 
43
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
В любой изолированной системе запас энергии остаётся постоянным. [2] Это — формулировка Дж. П. Джоуля
В научной и учебной литературе можно встретить варианты формулировок первого начала, отличающиеся знаками ( 



 |
МАЙЕРА УРАВНЕНИЕ — ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и пост, объёме СV 1 кмоля идеального газа: 



Адиабатный процесс. Уравнение Пуассона для адиабатного процесса. Уравнение адиабаты (уравнение Пуассона). Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой. Следовательно, для него характерно наличие хорошей изоляции ТС от внешней среды или высокая скорость термодинамического процесса, при которой теплообмен незначителен. Поскольку обратимые процессы, в отличии от адиабатных, являются бесконечно медленными, то о равновесности последних можно говорить только применительно к определенным областям ТС. Поскольку для адиабатического процесса dQ = 0, то dA = — dU. Следовательно, p·dV = — (m/m)·Cv·dT. (13.18) Следовательно, работа газа при адиабатическом расширении равна A1-2 = (m/m)·Cv·(T1 — T2). (13.19) Выразив величину P из уравнения Менделеева-Клапейрона и подставив ее в (13.18), после соответствующих преобразований получим уравнение адиабаты: T·Vg-1 = const или p·Vg = const. (13.20) Уравнение (13.20) называется также уравнением Пуассона. На диаграмме P-V адиабата испытывает более резкое падание, чем изотерма (см. рис. 13.4), т.е. в любой точке кривой модуль производной от давления по объему для нее больше. Действительно, из уравнения адиабаты можно показать, что dp/dV = — g·p/V > p/V.
Коэффициент Пуассона (обозначается как 

При приложении к телу растягивающего усилия оно начинает удлиняться в продольном направлении, а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз относительное уменьшение поперечного размера деформируемого тела больше относительного увеличения его длины, при его растяжении. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.




45
Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии, тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. (Возможно использование изменения не только объёма, но и формы рабочего тела, как это делается в твёрдотельных двигателях, где в качестве рабочего тела используется вещество в твёрдой фазе.) Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем.
Виды тепловых двигателей, история создания и применение этих видов двигателей.
a)пароваямашина
b) двигатель внутреннего сгорания
c) дизельный двигатель
d) паровая турбина
e) реактивный двигатель
Двигатель Стирлинга
Поршневой двигатель внутреннего сгорания
Роторный (турбинный) двигатель внешнего сгорания
В термодинамике цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов [1] . В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником
Описание цикла Карно
Цикл Карно в координатах T—S
Пусть тепловая машина состоит из нагревателя с температурой 

Цикл Карносостоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру 

2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника 
3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру 

4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
КПД тепловой машины Карно
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

Отсюда коэффициент полезного действия тепловой машины Карно равен
46.Трмодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.
Термодинамическое определение энтропии
Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропиитермодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:
Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.
Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
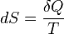
где 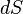

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).
Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому 
Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамикипозволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).
Существуют несколько эквивалентных формулировок второго закона термодинамики:
Постулат Клаузиуса: «Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому» [1] (такой процесс называется процессом Клаузиуса).
Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).
Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло 



С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.
Таким образом, постулаты Клаузиуса и Томсона эквивалентны.
Другая формулировка второго начала термодинамики основывается на понятии энтропии:
«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).
Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.
Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид [2] :
Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния 

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны.
Ограничения вывода формулы для дифференциала энтропии, данного Клаузиусом, заключаются в предположении об идеальности газа, свойства которого приводят к существованию интегрирующего множителя. Этот недостаток был устранен Каратеодори в работе «Об основаниях термодинамики» (1909). Каратеодори рассматривал множество состояний, достижимых адиабатическим путем (т.е. без теплообмена с окружающей средой). Уравнение, описывающее такое множество этих состояний в дифференциальной форме, является пфаффовой формой. Используя известные из анализа условия интегрируемости пфаффовых форм, Каратеодори пришел к следующей формулировке второго закона:
В окрестности любого состояния системы существуют состояния, не достижимые адиабатическим путем.
Такая постановка не ограничивает системы, подчиняющихся второму закону термодинамики, только идеальными газами и телами, способными совершать замкнутый цикл при взаимодействии с ними. Физический смысл аксиомы Каратеодори повторяет формулировку Клаузиуса.
Электри́ческий заря́д — это связанное с телом свойство, позволяющее ему быть источником электрического поля и участвовать в электромагнитных взаимодействиях. Заряд является количественной характеристикой. Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1А за время 1с. Впервые электрический заряд был введён в законе Кулона в 1785 году. Заряд в один кулон очень велик. Если бы два носителя заряда (q1 = q2 = 1Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9×109 H.Свойства электрического заряда
Заряд бывает двух видов, называемых положительным и отрицательным:
заряды одного вида отталкиваются друг от друга, заряды разных видов — притягиваются, причем сила отталкивания равна по модулю силе притягивания;
число положительных и отрицательных зарядов во Вселенной одинаковое.
Полный электрический заряд изолированной системы сохраняется. Закон Кулона и пpинцип супеpпозиции полей. Электpостатика лекции и конспекты по физике
Электрический заряд релятивистски инвариантен, т. е. его величина не зависит от скорости системы отсчета, как бы велика она ни была.
Величина заряда может принимать только дискретные значения:
минимальный заряд частицы e = 1.60·1019 Кл;
любой заряд q кратен минимальному, т. е. q=Ne, где N — целое число;
минимальные положительный и отрицательный заряды равны по абсолютной величине.
Закон сохранения заряда: в изолированной системе алгебраическая сумма зарядов остается постоянной величиной при всех изменениях внутри системы.
Изолированной называется система тел, которая не обменивается зарядами с внешней средой.
ва одноименных заряда, будь то два протона либо два электрона сопротивляются сближению и пытаются удалиться друг от друга. Этот процесс обычно называют отталкиванием. Первый закон описывающийвзаимодействие электрических зарядов говорит: заряды с одинаковым знаком (т. е. одноименные) отталкиваются друг от друга (рис.2.1.). Второй закон взаимодействия электрических зарядов гласит: разноименные (заряды с разным знаком) притягиваются друг к другу.
Отрицательно заряженные электроны притягиваются к положительно заряженным протонам в ядре атома. Почему же электрон остается на орбите и не падает на ядро? Это происходит в результате того, что сила притяжения электрона уравновешивается центростремительной силой, возникающей за счет вращения электрона вокруг ядра.
Значение величины сил отталкивания и притяжения, существующих между двумя заряженными телами, зависит от следующих факторов: расстояния между телами и их зарядов.
Заряд отдельного электрона очень мал, поэтому в практике не используется. Принятой в мире единицей измерения заряда является кулон (Кл). Она названа в честь французского ученого Шарля Кулона, обозначается буквой Q. Один кулон это 6,28*10 18 зарядов электронов.
Электрические заряды возникают за счет смещения электронов. Когда имеется дефицит электронов в одной точке и избыток в другой, как мы уже говорили, возникает разность потенциалов. Если две точки, между которыми существует разность потенциалов, соединить проводником, то по проводнику потекут электроны. Тогда этот поток электронов называется электрическим током.
Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами.
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
где 




Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга [1] .
Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.
Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля.
Основные характеристики электростатического поля: напряженность,потенциал
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 


Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном множителе).
📺 Видео
Сложение взаимно перпендикулярных колебанийСкачать

Сложение колебаний, Киевнаучфильм, 1978Скачать
67. Сложение колебанийСкачать

Фигуры ЛиссажуСкачать

Физика | Равномерное движение по окружностиСкачать

Урок 337. Сложение колебаний одной частоты. Метод векторных диаграммСкачать

4 Фигуры ЛиссажуСкачать

Урок 340. Сложение колебаний кратных частот. Гармонический анализ и синтезСкачать

Сложение двух сил, направленных по одной прямой | Физика 7 класс #22 | ИнфоурокСкачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Фигуры Лиссажу: осциллограф.Скачать

MathCAD в физике (ч.10, сложение перпендикулярных колебаний, фигуры Лиссажу)Скачать

Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Физика - движение по окружностиСкачать

Урок 336. Векторное представление колебанийСкачать

Урок 338. Сложение колебаний близких частот. БиенияСкачать

Галилео. Эксперимент. Фигуры ЛиссажуСкачать

Урок 327. Гармонические колебанияСкачать

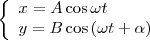 (1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
(1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как 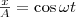
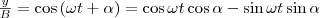 и заменяя во втором уравнении
и заменяя во втором уравнении  на
на 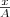 и
и 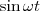 на
на 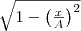 , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: 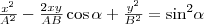 (2) Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2, . ). В этом случае эллипс становится отрезком прямой
(2) Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес: 1) α = mπ (m=0, ±1, ±2, . ). В этом случае эллипс становится отрезком прямой 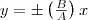 (3) где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2. ). В этом случае уравнение станет иметь вид
(3) где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями; 2) α = (2m+1)(π/2) (m=0, ± 1, ±2. ). В этом случае уравнение станет иметь вид 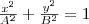 (4) Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу.
(4) Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу. 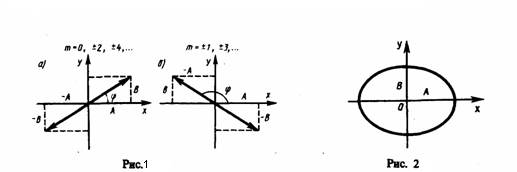 Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ). Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.