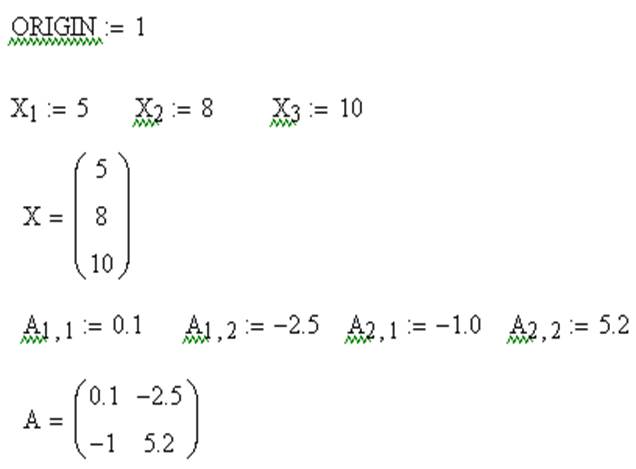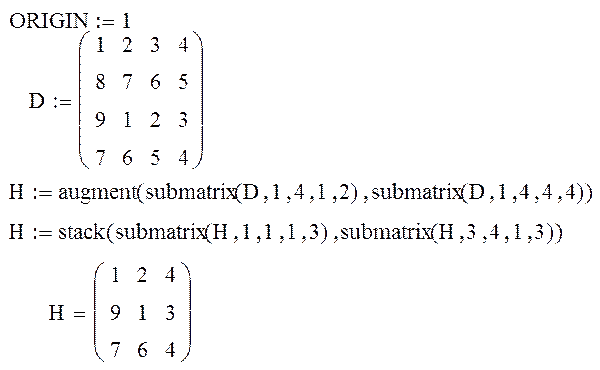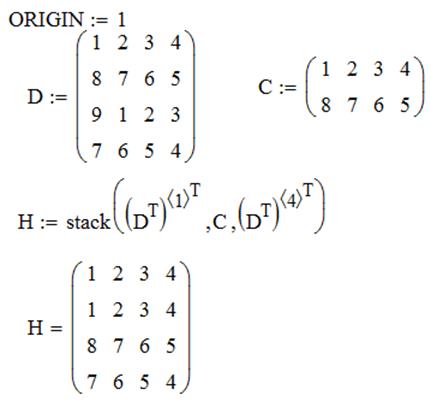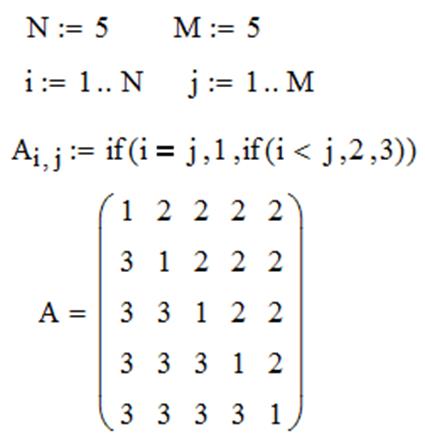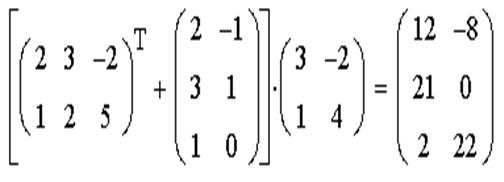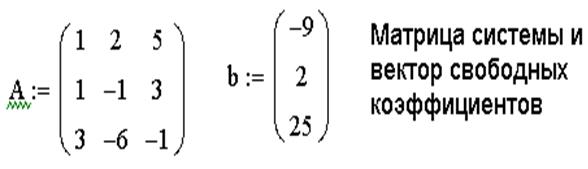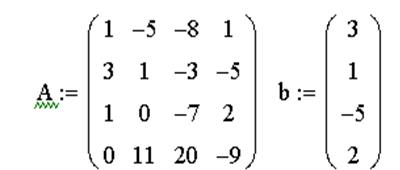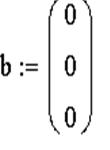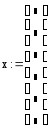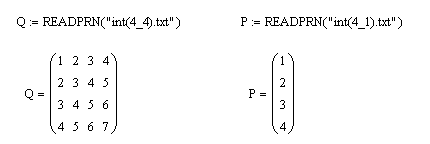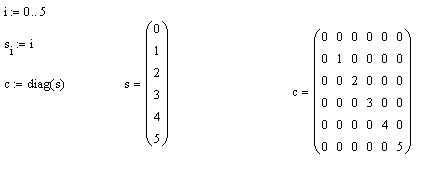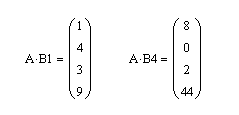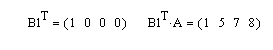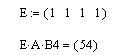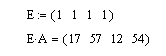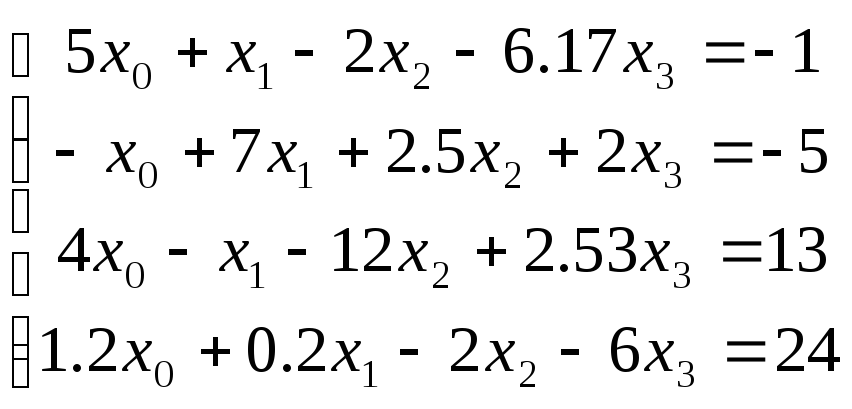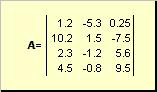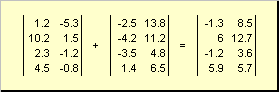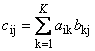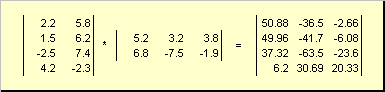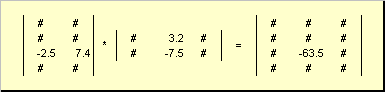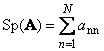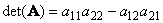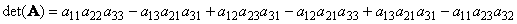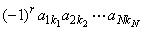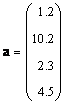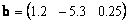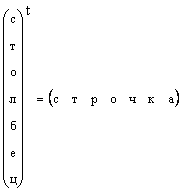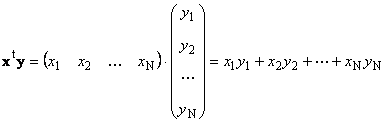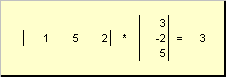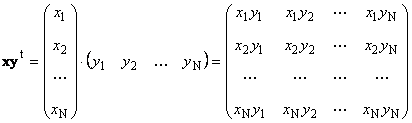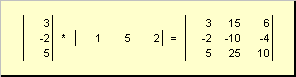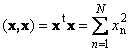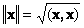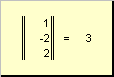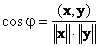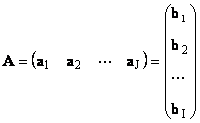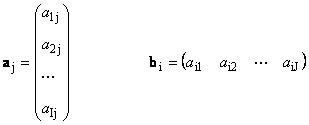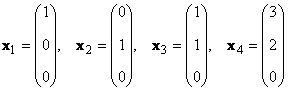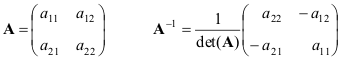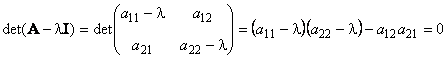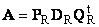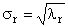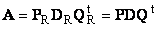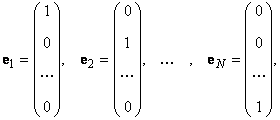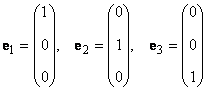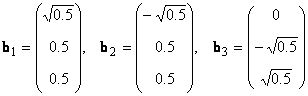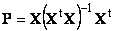Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
ПанельMatrix содержит следующие кнопки:


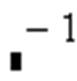

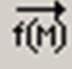
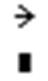
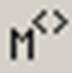






Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
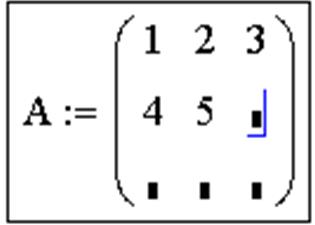
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=<aij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле 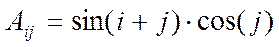
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
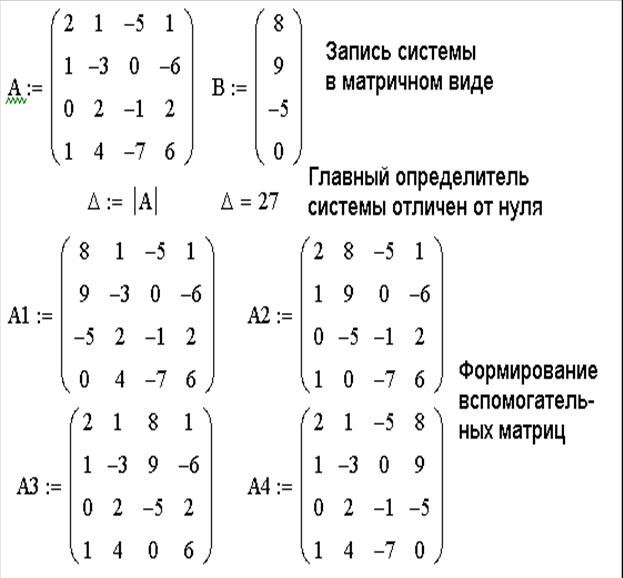
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
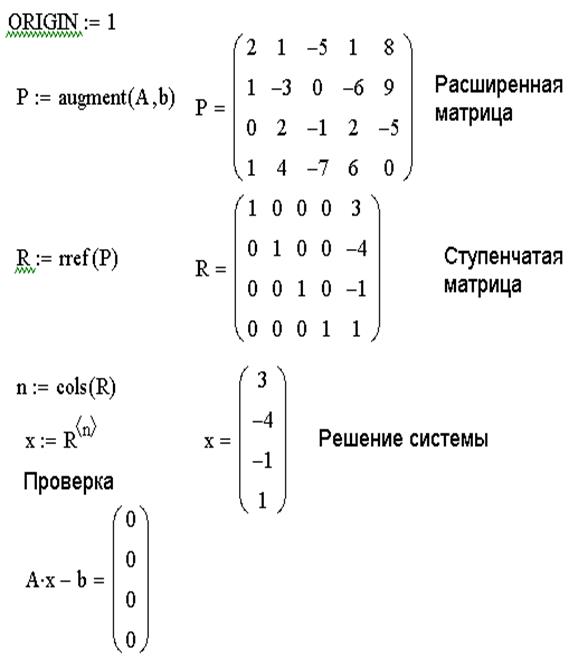
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
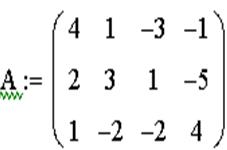
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
- Сформировать вектор из матрицы
- Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
- 3.1. Создание векторов и матриц
- 3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
- 3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
- Содержание
- 1. Базовые сведения
- 1.1 Матрицы
- 1.2. Простейшие операции с матрицами
- 1.3. Умножение матриц
- 1.4. Квадратные матрицы
- 1.5. След и определитель
- 1.6. Векторы
- 1.7. Простейшие операции с векторами
- 1.8. Произведения векторов
- 1.9. Норма вектора
- 1.10. Угол между векторами
- 1.11. Векторное представление матрицы
- 1.12. Линейно зависимые векторы
- 1.13. Ранг матрицы
- 1.14. Обратная матрица
- 1.15. Псевдообратная матрица
- 1.16. Умножение вектора на матрицу
- 2. Дополнительная информация
- 2.1. Системы линейных уравнений
- 2.2. Билинейные и квадратичные формы
- 2.3. Положительно определенные матрицы
- 2.4. Разложение Холецкого
- 2.5. Полярное разложение
- 2.6. Собственные векторы и собственные значения
- 2.7. Собственные значения
- 2.8. Собственные векторы
- 2.9. Эквивалентные и подобные матрицы
- 2.10. Приведение матрицы к диагональному виду
- 2.11. Разложение по сингулярным значениям (SVD)
- 2.12. Линейное пространство
- 2.13. Базис линейного пространства
- 2.14. Геометрическая интерпретация
- 2.15. Множественность базисов
- 2.16. Подпространство
- 2.17. Проекция на подпространство
- Заключение
- Векторы и матрицы в MathCAD
- Сформировать вектор из элементов матрицы
Видео:Матрицы и векторыСкачать

Сформировать вектор из матрицы
Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).
Матричные вычисления в MathCAD можно условно разделить на три основных типа.
К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).
Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.
И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.
В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.
Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: 

Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.
Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

3.1. Создание векторов и матриц
В системе предусмотрены различные возможности задания векторов и матриц:
Определение матрицы последовательным заданием каждого элемента.
С помощью индексированных переменных.
С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.
Задание с помощью элементов программирования.
Применение встроенных функций.
Через связь с другим приложением, например Excel.
Создание таблицы данных.
Чтение из внешнего файла.
Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение. Предоставим два варианта решения этой задачи:
с помощью индексированной переменной;
с помощью команды Insert→Matrix.
Вариант а
Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.
Рис. 3.1. Формирование вектора с использованием индексированной переменной
Вариант b
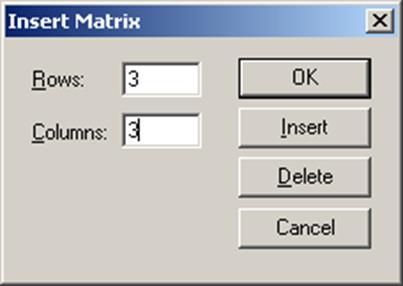
Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.
После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.
Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.
Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.
Рис. 3.3. Чтение данных из файлов
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.
Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
Х -1 – получить обратную матрицу
|X| – вычислить детерминант
М Т – транспонировать
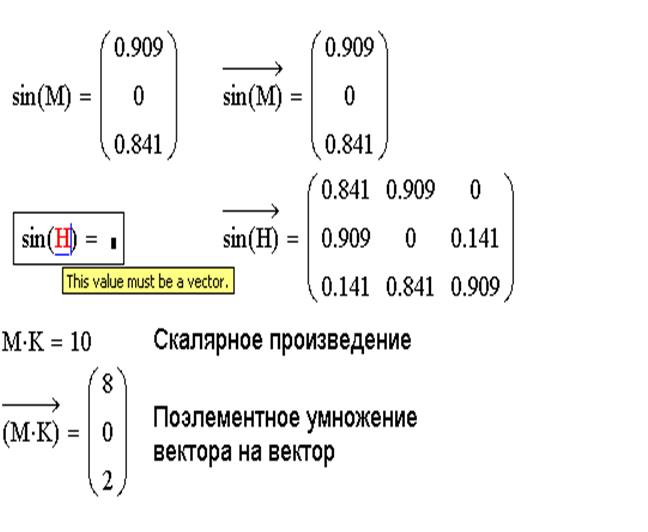
М – из матрицы взять вектор-столбец
v – получить сумму элементов

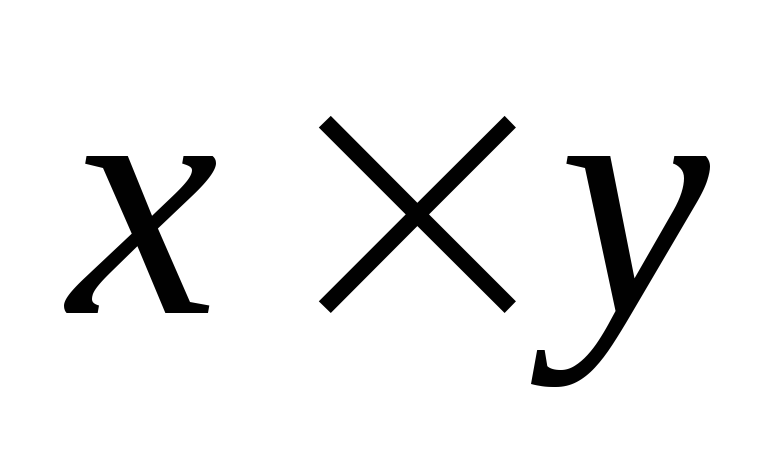
Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»
На рис. 3.5 представлены вычисления с использованием операций над матрицами.
Рис. 3.5. Примеры матричных вычислений в MathCAD
Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.
Рис. 3.6. Формирование диагональной матрицы
Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.
Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»
Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.
Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.
Рис. 3.8. Объединения двух матриц по правилу «друг под другом»
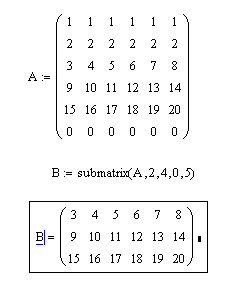
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.
Рис. 3.9. Выделение подматрицы из заданной матрицы
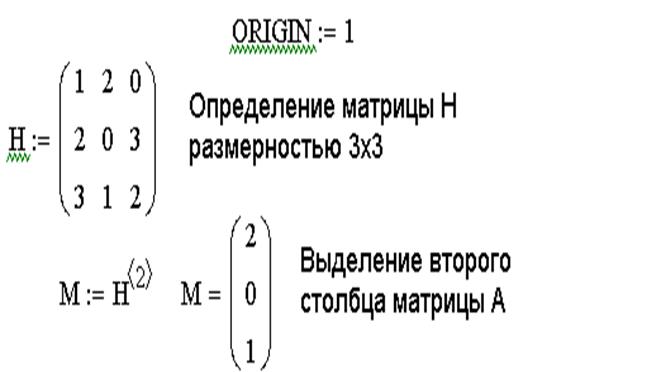
Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.
Решение. Для получения векторных значений можно воспользоваться командой М (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.
Рис. 3.10. Выделение векторных значений из заданной матрицы
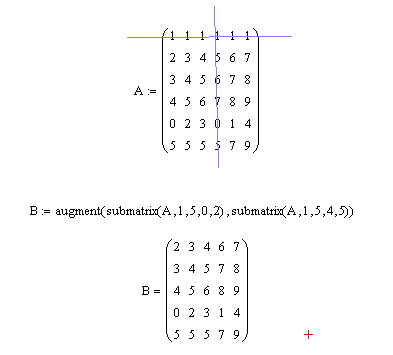
Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.
Рис. 3.11. Выделение минора из заданной матрицы
Видео:Ввод и вывод матриц в c++Скачать

3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
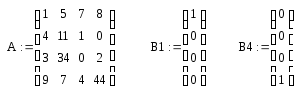
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.
Рис. 3.12. Выделение векторных значений из заданной матрицы
Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).
Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.
Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.
Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:
Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:
Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).
Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Видео:7. MathCad. Векторы и матрицыСкачать

3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:

Введем следующие обозначения:
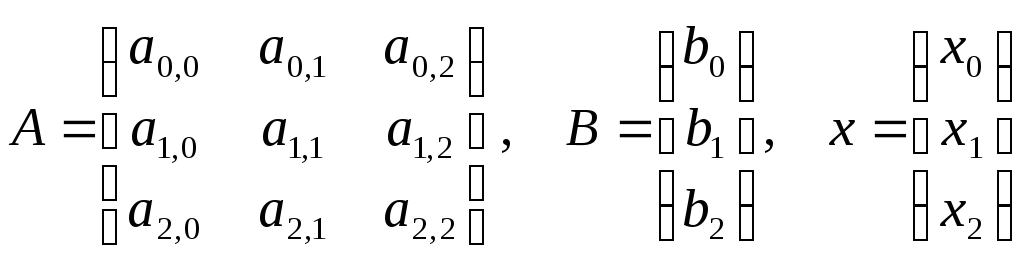
А – матрица коэффициентов;
В – вектор свободных членов;
х – вектор неизвестных.
В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:
Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.
В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:
Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:
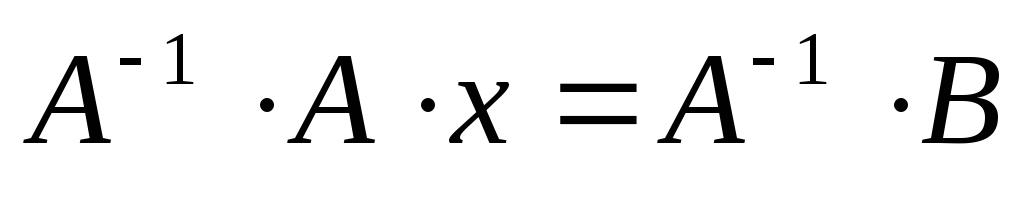
Воспользуемся свойством, что 
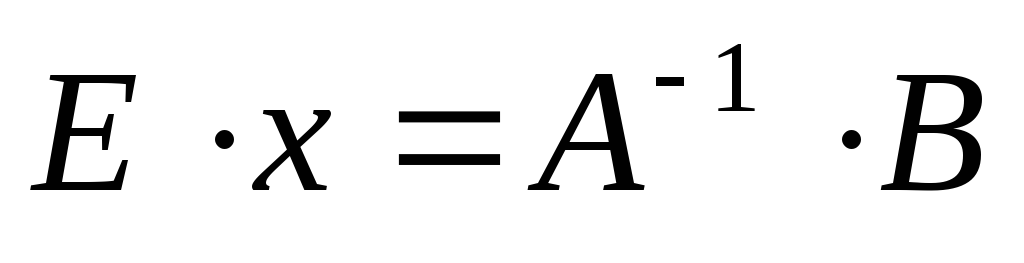
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:

где (3.6) – решение системы (3.3).
Пример 15. Требуется найти решение следующей системы линейных уравнений:
Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.
Видео:Занятие 12. Векторы и матрицыСкачать

Содержание
В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.
Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.
Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.
Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.
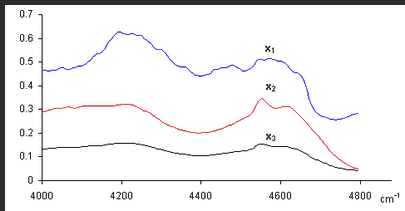
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?
Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
Видео:Программирование на С++. Урок 70. ВекторСкачать

1. Базовые сведения
Видео:Как сделать вектор из картинки. Простой и быстрый метод за 5 шагов.Скачать
1.1 Матрицы
Матрицей называется прямоугольная таблица чисел, например
Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как . Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.
Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.
Видео:Метод конечных элементов. Основы 1.2.2 - Сборка матриц жесткости. Глобальная матрица жесткостиСкачать

1.2. Простейшие операции с матрицами
Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —
Рис. 3 Умножение матрицы на число
Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,
Рис. 4 Сложение матриц
В результате умножения на число и сложения получается матрица той же размерности.
Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .
Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = , то A t = . Например
Рис. 5 Транспонирование матрицы
Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1.3. Умножение матриц
Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа
Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —
Рис.6 Произведение матриц
Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B
Рис.7 Элемент произведения матриц
Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .
Видео:vector | Библиотека стандартных шаблонов (stl) | Уроки | C++ | #1Скачать

1.4. Квадратные матрицы
Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
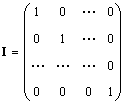
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
Очевидно AI = IA = A .
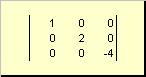
Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например
Рис. 8 Диагональная матрица
Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например
Рис. 9 Верхняя треугольная матрица
Аналогично определяется и нижняя треугольная матрица.
Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например
Рис. 10 Симметричная матрица
Матрица A называется ортогональной , если
Матрица называется нормальной если
Видео:Программирование на С++. Урок 71. Пример работы с вектором. Двумерный вектор.Скачать

1.5. След и определитель
Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,
Рис. 11 След матрицы
Sp(α A ) = α Sp( A ) и
Sp( A + B ) = Sp( A )+ Sp( B ).
Можно показать, что
Sp( A ) = Sp( A t ), Sp( I ) = N ,
Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда
Для матрицы (3×3) определитель будет равен
В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен
Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,
Рис. 12 Определитель матрицы
Отметим только очевидные свойства:
det( I ) = 1, det( A ) = det( A t ),
det( AB ) = det( A )det( B ).
Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

1.6. Векторы
Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например
Можно рассматривать и матрицы, состоящие из одной строки, например
Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .
Видео:MATLAB 04 Массивы и матрицыСкачать

1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,
Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными , если существует такое число α, что
Видео:#7. Реализация динамического массива на С++ с помощью std::vector | Структуры данныхСкачать

1.8. Произведения векторов
Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: x t y и xy t . Первое произведение
называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,
Рис. 14 Внутреннее (скалярное) произведение
называется внешним . Его результат — это матрица размерности ( N × N ). Например,
Рис. 15 Внешнее произведение
Векторы, скалярное произведение которых равно нулю, называются ортогональными .
Видео:Программирование на Си - Урок 11 - многомерные массивы и матрицыСкачать

1.9. Норма вектора
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение
Рис. 16 Норма вектора
Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

1.10. Угол между векторами
Скалярное произведение определяет и угол φ между двумя векторами x и y
Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.
Видео:Собственные векторы и собственные значения матрицыСкачать

1.11. Векторное представление матрицы
Каждую матрицу A размера I × J можно представить как набор векторов
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A
Видео:Урок 7. МКЭ в Mathcad. Матрицы инциденций, жесткости и вектор перемещений ДМСкачать
1.12. Линейно зависимые векторы
Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор
y = α 1 x 1 + α 2 x 2 +. + α K x K
называется линейной комбинацией векторов x k .
Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0
Видео:Превращаем картинку в 3д модификаторамиСкачать

1.13. Ранг матрицы
Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе
имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.
Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.
Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.
rank( A ) = rank( A t ).
1.14. Обратная матрица
Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det( A ) ≠ 0 или rank( A ) = N .
Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,
Рис. 17 Обращение матрицы
Приведем формулы для простейшего случая — матрицы 2×2
Если матрицы A и B невырождены, то
1.15. Псевдообратная матрица
Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что
Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.
Если число столбцов меньше числа строк, то
A + =(A t A) −1 A t
Рис. 1 7a Псевдообращение матрицы
Если же число столбцов больше числа строк, то
A + =A t (AA t ) −1
1.16. Умножение вектора на матрицу
Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,
Рис. 18 Умножение вектора на матрицу
Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что
A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .
Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .
2. Дополнительная информация
2.1. Системы линейных уравнений
Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение
относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда
rank( A ) = rank( B ) = R ,
где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.
Если R = I = J , то решение единственно
Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.
2.2. Билинейные и квадратичные формы
Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.
2.3. Положительно определенные матрицы
Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,
Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.
2.4. Разложение Холецкого
Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой
Рис. 19 Разложение Холецкого
2.5. Полярное разложение
Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление
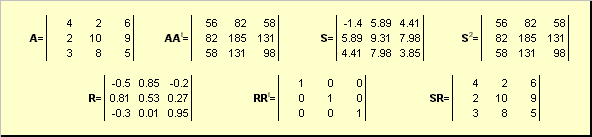
где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:
S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .
Рис. 20 Полярное разложение
Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .
2.6. Собственные векторы и собственные значения
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если
где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
Рис. 21 Собственные значения
Набор собственных значений λ 1 . λ N матрицы A называется спектром A .
Спектр обладает разнообразными свойствами. В частности
det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений
Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.
Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
2.9. Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что
Эквивалентные матрицы имею один и тот же ранг.
Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что
Матрица T называется преобразованием подобия.
Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.
2.10. Приведение матрицы к диагональному виду
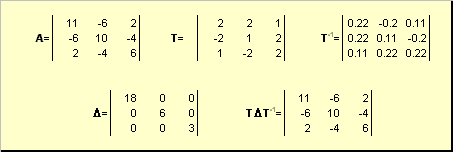
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).
Рис. 23 Приведение к диагональному виду
2.11. Разложение по сингулярным значениям (SVD)
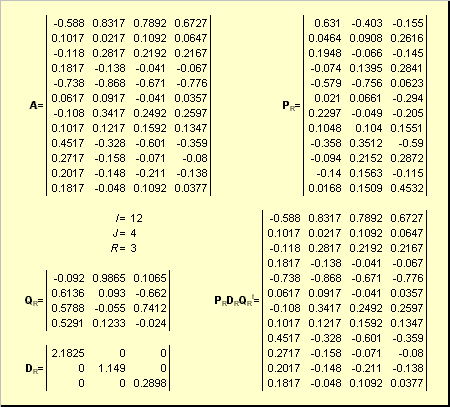
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —
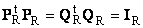
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;
AA t p r = λ r p r ;
Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;
A t Aq r = λ r q r .
D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —
Рис. 24 SVD разложение
Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что
2.12. Линейное пространство
Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.
2.13. Базис линейного пространства
Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .
2.14. Геометрическая интерпретация
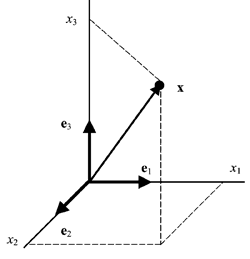
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).
Рис. 25 Координатное пространство
2.15. Множественность базисов
В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса
можно установить и другой ортонормированный базис, например
Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .
2.16. Подпространство
Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов
x = α 1 x 1 + α 2 x 2 +. + α K x K
О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .
2.17. Проекция на подпространство
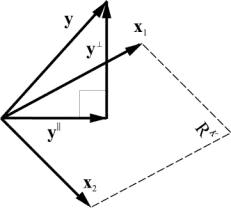
Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде
где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .
Рис. 26 Проекция на подпространство
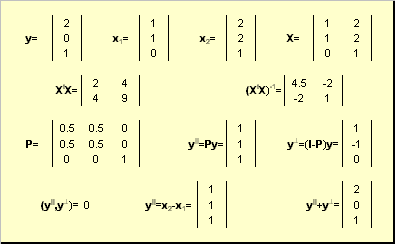
Проекцию y || можно представить как результат действия проекционной матрицы P
Проекционная матрица определяется как
Рис. 27 Проекционное разложение
Заключение
Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.
Векторы и матрицы в MathCAD
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
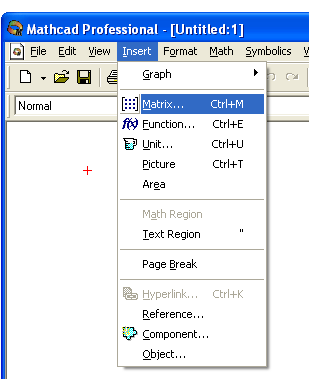
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
ПанельMatrix содержит следующие кнопки:

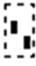

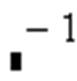

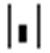
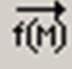
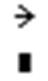
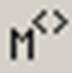
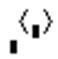

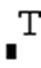





Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле 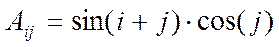
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
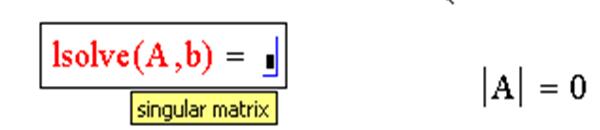
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
Сформировать вектор из элементов матрицы
Задана матрица A (m*n). сформировать вектор В, элементами которого являются эл-ты матр А, удовлетворяющие условию с≤|aij|≤d.
вот сделал формирование самой матрицы. а как отсюда вектор этот вытащить не догоняю..
const
n1 = 20; m1 = 20;
type
index1 = 1..n1;
index2 = 1..m1;
matrix = array[index1, index2]of real;
var
n, i: index1;
m, j: index2;
A: matrix;
begin
write(‘введите кол-во строк n= ‘);readln(m);
write(‘введите кол-во столбцов m= ‘);readln(n);
writeln(‘_____________________________________’);
writeln(‘исходная матрица А’);
for i:=1 to m do
begin
for j:=1 to n do
begin
a[i,j]:=-30+random(50);
write(a[i,j]:4);
end;
writeln;
end;
writeln(‘_____________________________________’);
end.