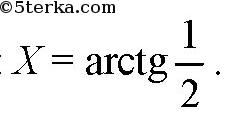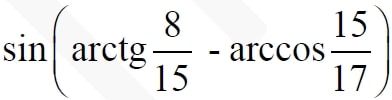Точка, лежащая на окружности верхнего основания цилиндра, соединена с точкой, лежащей на окружности нижнего основания. Угол между проведенной прямой и осью цилиндра составляет 45. Найдите радиус цилиндра, если длина отрезка, соединяющего выбранные точки, равна 7√2, а радиус цилиндра равен его высоте.
Построим параллельную прямую оси цилиндра O’O1′, получаем, что треугольники AO’Z A1O1’Z равны (они оба прямоугольные, равнобедренные треугольники)
Значит O1’Z=O’Z, значит O1Z=O’Z=r/2, O1A1=r/2 и O’A=r/2 (равнобедренные треугольники)
По т Пифагора ( AZ=sqrtfrac )
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
6. В равностороннем цилиндре (диаметр равен высоте цилиндра) точка окружности верхнего основания соединена с точкой окружности нижнего основания.
Угол между радиусами, проведенными в эти точки, равен 60°. Найдите угол X между проведенной прямой и осью цилиндра.
Через данные точки А и С проведем плоскость ABCD, параллельную оси. Соединим точки В и О1. Угол между радиусами, проведенными в данные точки А и С соответственно из О и O1 будет равен углу ∠BO1C = 60°.
Следовательно, равнобедренный ΔBO1С является равносторонним и BС = 0,5 = К. Искомый угол X между проведенной прямой А С и осью цилиндра равен ∠BAC. В прямоугольнике ABCD AB=D=2R (по условию). Тогда из прямоугольного ΔABC
Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №6
к главе «§21.Тела вращения».
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Решение варианта Ларина №350 ЕГЭ
Решение и ответы заданий № 1–12 варианта №350 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
Если Сергей купит 15 тетрадей, то у него останется 7 рублей, если же он купит 20 тетрадей, то ему не хватит 8 руб. Сколько денег у Сергея? Ответ дайте в рублях.
Задание 2.
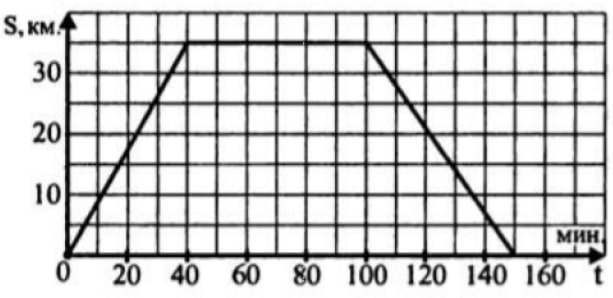
Грузовая машина отправилась из магазина на склад, где провела некоторое время в процессе погрузки, и вернулась обратно по тому же самому маршруту. На рисунке изображен график движения этой машины: по оси абсцисс откладывается время (в минутах) с момента выезда машины от магазина, по оси ординат – расстояние от машины до магазина (в км, вдоль маршрута движения). Найдите по графику скорость машины при движении на склад. Ответ выразите в км/ч.
Задание 3.
Какой наименьший радиус может иметь окружность с центром в точке А(–9; –6), если она касается окружности радиуса 1 с центром в точке В(15; 12)?
Задание 4.
Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная. Ответ округлите до сотых.
Задание 5.
Решите уравнение: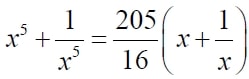 
Если уравнение имеет несколько корней, в ответе укажите наименьший корень.
Задание 6.
Площадь равнобедренной трапеции равна 180 см 2 . Найдите длину верхнего основания, если боковые стороны равны по 13 см, а нижнее основание 20 см. Ответ дайте в см.
Задание 7.
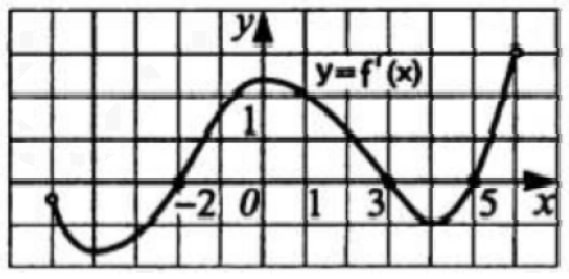
Функция y = f(x) определена на промежутке (–5;6). На рисунке изображен график ее производной. Найдите точку, в которой функция y = f(x) принимает наименьшее значение.
Задание 8.
Точка, лежащая на окружности верхнего основания цилиндра, соединена с точкой, лежащей на окружности нижнего основания. Угол между проведенной прямой и осью цилиндра составляет 45°. Найдите радиус цилиндра, если длина отрезка, соединяющего выбранные точки, равна 7√2 , а радиус цилиндра равен его высоте.
Задание 9.
Вычислить: 
Задание 10.
Уравнение процесса, в котором участвовал газ, записывается в виде P·V a = const, где P (Па) – давление в газе, V – объем газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение объёма газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза?
Задание 11.
Дорога проходит через пункты А и В. Велосипедист выехал из А по направлению к В. Одновременно с ним из пункта В вышли с равными скоростями два пешехода: первый в пункт А, а второй – в противоположном направлении. Велосипедист проехал от А до В за 0,5 ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время (в часах) движения велосипедиста от начала движения до встречи с первым пешеходом?
Задание 12.
Найдите наименьшее значение функции y = 5x 3 – x|x + 1| на отрезке [–2;0].
💥 Видео
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать
✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать
№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать
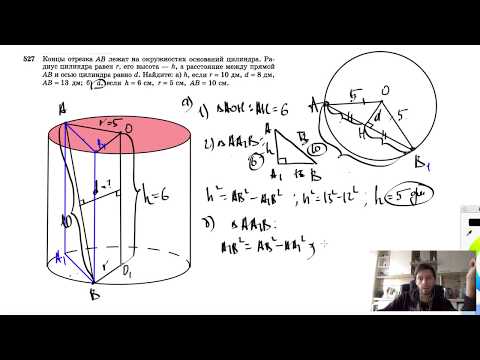
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать
11 класс, 27 урок, Сечения цилиндрической поверхностиСкачать
11 класс, 14 урок, Понятие цилиндраСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать
№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать
Практика Стереометрия№5 (профиль)Скачать
СТЕРЕОМЕТРИЯ ЗА 30 МИНУТСкачать
Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать
Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать
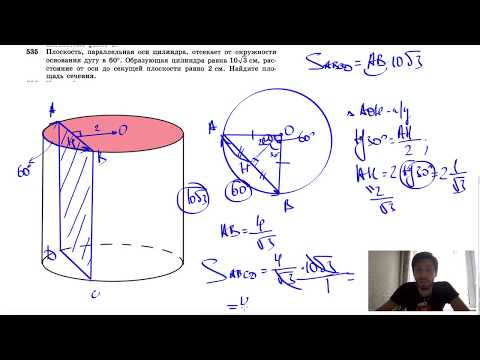
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
Вариант ФИПИ #12 все задачи (математика ЕГЭ база)Скачать
Цилиндр. Определение, свойства, формулы.Скачать
