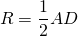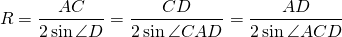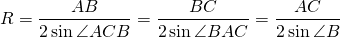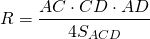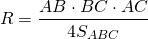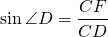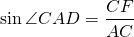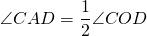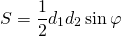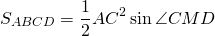Условие
В равнобокую трапецию вписана окружность.
А) Докажите, что диаметр окружности равен среднему геометрическому длин оснований трапеции.
(Средним геометрическим двух положительных чисел а и b называется значение выражения sqrt(ab))
Б) Найдите площадь четырехугольника с вершинами в точках касания окружности со сторонами трапеции, если известно, что длины оснований трапеции 8 и 18.
Решение
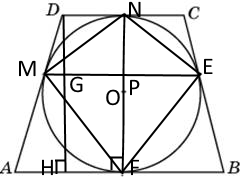
А)NF-диаметр вписанной окружности
Если AB=b, DC=a
То требуется доказать, что NF=sqrt(ab)
DH-высота трапеции, значит DH=NF
Так как трапеция равнобедренная, то AH=(b-a)/2
По свойству касательных:
AF=AM=b/2
MD=DN=a/2
Тогда, AD=b/2+a/2=(b+a)/2
Из треугольника ADH по теореме Пифагора:
DH=sqrt(AD^2-AH^2)=sqrt(((b+a)/2)^2-((b-a)/2)^2)=sqrt((b^2+2ab+a^2-b^2+2ab-a^2)/4)=sqrt(ab)
NF=sqrt(ab)
Что и требовалось доказать
Б)DC=8, AB=18 по условию
Тогда AM=18:2=9
MD=8:2=4
AH=(18-8)/2=5
Треугольник MDG подобен треугольнику ADH(по вум углам):
AD/MD=AH/MG
MG=(MD*AH)/AD
MG=(4*5)/(9+4)=20/13
ME=2*MG+DC=2*20/13+8=40/13+8=144/13
Ответ:864/13
Видео:Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапецииСкачать
В равнобокую трапецию с основаниями 4 и 9 вписана окружность найдите площадь четырехугольника
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.
$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Докажем, например, утверждение $$ 4.^$$ .
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
| `d^2=c^2+ab`. |
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).
По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`
(т. к. угол `BDK` — это угол между диагоналями трапеции).
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.
$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.
Видео:Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать
Трапеция вписана в окружность
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
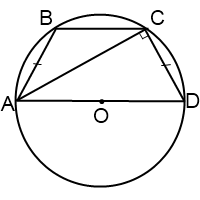
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
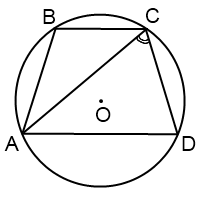
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
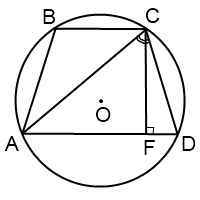
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
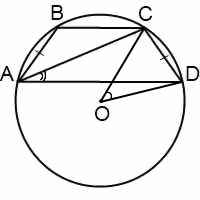
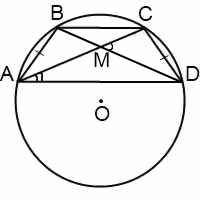
В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
🎥 Видео
Задача про трапецию, описанную около окружностиСкачать
8 класс, 15 урок, Площадь трапецииСкачать
КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать
Геометрия В равнобедренную трапецию вписана окружность радиуса R. Верхнее основание трапеции в 2Скачать
Окружность, вписанная в трапециюСкачать
Задание 24 ОГЭ по математике #4Скачать
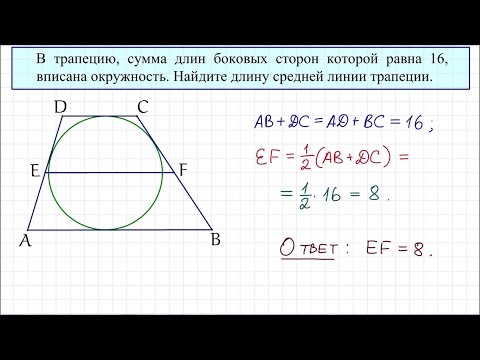
Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать
16 ЗАДАНИЕ ОГЭ ИЩЕМ УГОЛ А В ТРАПЕЦИИ ИЗ КРУГАСкачать
№599. Найдите площадь равнобедренной трапеции с основаниями 2 см и 6 см, если уголСкачать
Найдите площадь четырехугольника с вершинами в точках касания окружности со сторонами трапецииСкачать
Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
В равнобедренную трапецию, периметр которой равен 180, а площадьравна 1620, можно вписать...Скачать
Основания трапеции равны 4 и 10 Найдите больший из отрезков на которые делит среднюю линию диагональСкачать
Задание из ЕГЭ: трапеция в окружности #геометрия #егэ2023 #трапеция #окружностьСкачать
ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать
