Основные определения и свойства призм. Теорема Эйлера Основные определения и свойства призм. Теорема Эйлера |
 Виды призм. Прямые и наклонные призмы. Правильные призмы Виды призм. Прямые и наклонные призмы. Правильные призмы |
 Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды Примеры призм. Треугольные призмы. Четырехугольные призмы. Параллелепипеды |
Видео:10 класс, 30 урок, ПризмаСкачать

Основные определения и свойства призм. Теорема Эйлера
Утверждение 1. Каждый из n четырехугольников
Для остальных четырехугольников доказательство проводится аналогично.
называют боковыми гранями призмы . Совокупность всех боковых граней призмы составляет боковую поверхность призмы .
Утверждение 2 . Все боковые ребра призмы равны.
Это утверждение непосредственно вытекает из утверждения 1.
Замечание 1. В случае, когда не требуется делать специальных уточнений,
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
| + |
| – |
| = | 2 |
| + |
| – |
| = | 2 |
| + |
| – |
| – |
| = | 2 |
Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
то теорема Эйлера доказана.
Определение 7. Расстояние между плоскостями Расстояние между плоскостями , на которых лежат основания призмы, называют высотой призмы.
Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
Видео:Объем прямой призмы | Геометрия 11 класс #23 | ИнфоурокСкачать

Виды призм. Прямые и наклонные призмы. Правильные призмы
Существует следующая классификация призм.
Определение 8. Прямой призмой называют призму, боковые ребра которой перпендикулярны к плоскостям оснований. Призмы, боковые ребра которых не перпендикулярны к плоскостям оснований, называют наклонными призмами .
Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.
Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.
Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Примеры призм. Треугольные призмы. Четырехугольные призмы.
Параллелепипеды
| Призма | Рисунок | Свойства | |
| Наклонная треугольная призма |  | ||
| Прямая треугольная призма |  | ||
| Правильная треугольная призма |  | ||
| Наклонная четырехугольная призма |  | ||
| Прямая четырехугольная призма |  | ||
| Правильная четырехугольная призма |  | ||
| Параллелепипед |  | ||
| Прямой параллелепипед | 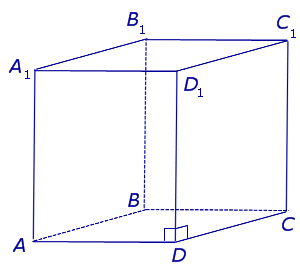 | ||
| Прямоугольный параллелепипед | 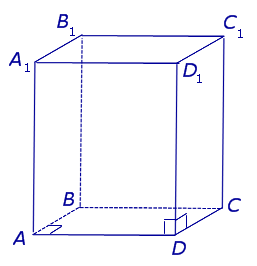 | ||
| Правильный параллелепипед |  | ||
| Куб | 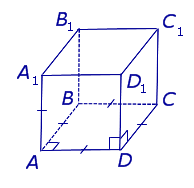 |
| Наклонная треугольная призма |
 |
ABС – произвольный треугольник.


ABСD – произвольный четырехугольник.

Свойства:
Наклонная четырехугольная призма, все грани которой паралллелограммы.
Противоположные грани параллелепипеда равны.
Все грани прямоугольного параллелепипеда являются прямоугольниками.


Свойства:
Правильный параллелепипед, у которого все грани равные квадраты.
У куба все ребра равны и попарно перпендикулярны.
Высота куба равна длине ребра.
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 14. Призма
Перечень вопросов, рассматриваемых в теме:
- Понятие призмы и виды призм;
- Элементы призмы: вершины, ребра, грани;
- Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
- Призма как модель реальных объектов;
- Пространственная теорема Пифагора.
Глоссарий по теме
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
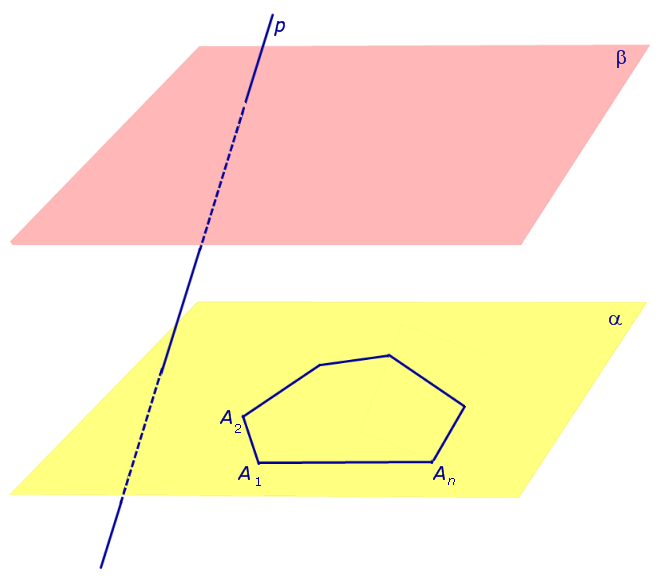
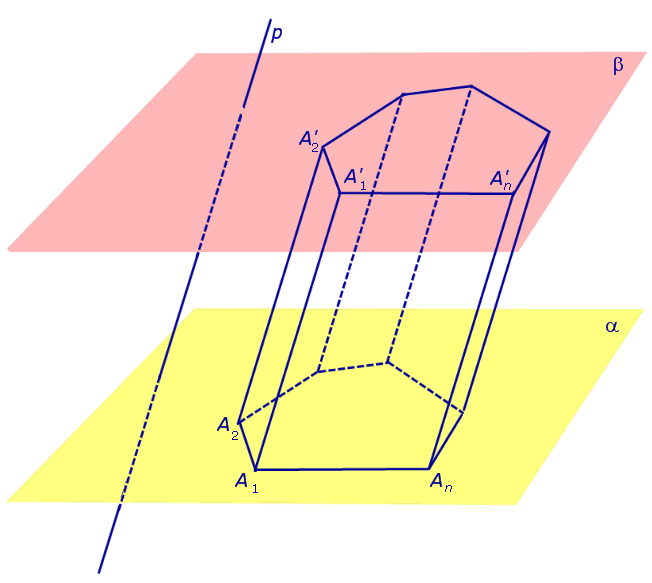
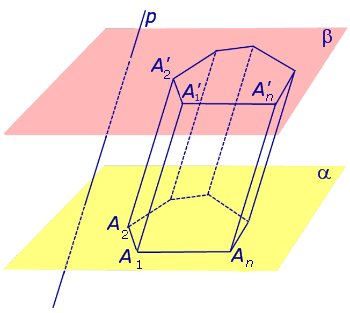
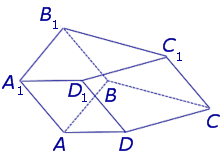
Рассмотрим два равных многоугольника А1А2. Аn и В1В2. Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Рисунок 1 – Призма
Заметим, что каждый из n четырехугольников (A1A2B1B2, . AnA1B1Bn) является параллелограммом. Убедимся в этом на примере четырехугольника A1A2B1B2. A1A2 и B1B2 параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А1В1 и А2В2 по условию. Таким образом, в четырехугольнике A1A2B1B2 противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
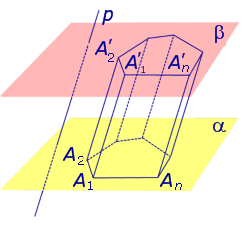
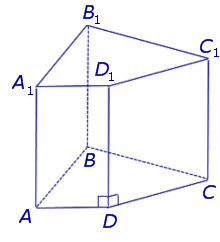
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
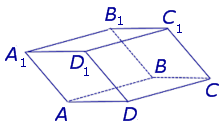
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
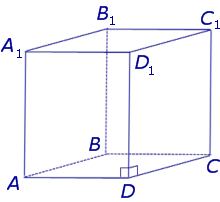
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С 2 =АА1 2 +АС 2 (1).
Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС 2 =ВС 2 +АВ 2 .
Подставив результат в (1), получим: А1С 2 =АА1 2 +ВС 2 +АВ 2 .
Так как в основании прямоугольник, то ВС=АD.
Таким образом, А1С 2 =АА1 2 +АD 2 +АВ 2 .
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Найдите для каждой картинки пару
1)

4)
6)
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Видео:Геометрия 10 класс (Урок№14 - Призма.)Скачать

Геометрические фигуры. Призма. Объем призмы.
Призма — многогранник, 2 грани это конгруэнтные (равные) многоугольники, которые лежат в
параллельных плоскостях, а оставшиеся грани — параллелограммы, имеющие общие стороны с
этими многоугольниками. Либо (что тоже самое) — это многогранник, основаниями которого
являются равные многоугольники, а боковыми гранями — параллелограммы.
Призма является разновидностью цилиндра.
Элементы призмы.
конгруэнтными многоугольниками, которые лежат
в плоскостях, параллельных друг другу.
Боковые грани (ABLK, BCML, CDNM, DEPN, EAKP) – каждая
из граней, не считая оснований. Все боковые грани – это
Боковая поверхность – сумма боковых граней.
Полная поверхность – сумма основания и боковой
Боковые ребра (AK, BL, CM, DN, EP) – общие стороны

Высота (KR) – отрезок, который соединяет плоскости, в них лежат основания призмы. Он
перпендикулярен этим плоскостям.
Диагональ (BP) – отрезок, который соединяет 2 вершины призмы, которые не принадлежат одной
Диагональная плоскость – плоскость, которая проходит через боковое ребро призмы, а также
Диагональное сечение (EBLP) – пересечение призмы и диагональной плоскости. В сечении получается
Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной
боковому ребру призмы.
Свойства призмы.
- Основания призмы – это равные многоугольники.
- Боковые грани призмы имеют вид параллелограмма.
- Боковые ребра призмы параллельные и равны.
- Площадь полной поверхности призмы = сумме площади её боковой поверхности и двойной
где P — периметр перпендикулярного сечения, l — длина бокового ребра.
- Площадь боковой поверхности прямой призмы:
где P — периметр основания призмы, h — высота призмы.
- Перпендикулярное сечение перпендикулярно всем боковым рёбрам призмы.
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих
- Перпендикулярное сечение перпендикулярно всем боковым граням.
- Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.

Привальная четырехугольная пирамида.
Свойства правильной четырехугольной призмы.
- Основания правильной четырехугольной призмы – это 2 одинаковых квадрата;
- Верхнее и нижнее основания параллельны;
- Боковые грани имеют вид прямоугольников;
- Все боковые грани равны между собой;
- Боковые грани перпендикулярны основаниям;
- Боковые ребра параллельны между собой и равны;
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям;
- Углы перпендикулярного сечения — прямые;
- Диагональное сечение правильной четырехугольной призмы является прямоугольником;
- Перпендикулярное (ортогональное сечение) параллельно основаниям.
Формулы для правильной четырехугольной призмы.
Виды призм.
Призма, у которой в основании лежит параллелограмм, является параллелепипедом.
Прямая призма — это призма, с перпендикулярными боковыми ребрами относительно плоскости основания.
Остальные призмы являются наклонными.
Правильная призма — прямая призма, в основании у нее лежит правильный многоугольник. Боковые
грани такой призмы — одинаковые прямоугольники.
Правильная призма, у которой боковые грани – квадраты (высота равна стороне основания), называется
полуправильным многогранником.
📽️ Видео
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Построение призмы высотой 30ммСкачать

№221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать

№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать
Как строить сеченияСкачать

Площадь поверхности призмы. 11 класс.Скачать

11 класс, 31 урок, Объем прямой призмыСкачать

Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. РЕШЕНИЕ!Скачать

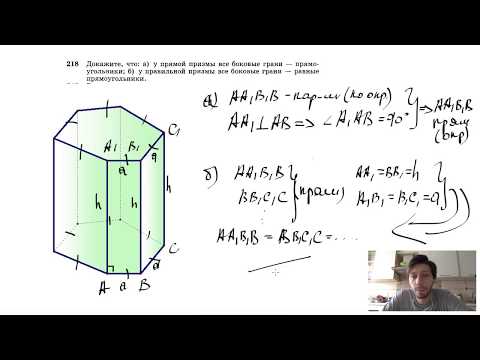
№218. Докажите, что: а) у прямой призмы все боковые грани — прямоугольники; б) у правильнойСкачать
Угол наклона плоскости общего положения относительно плоскостям проекцииСкачать

Геометрия В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребраСкачать

№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать