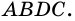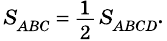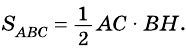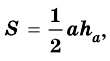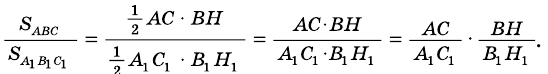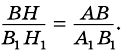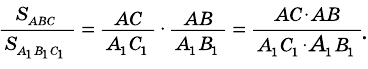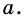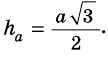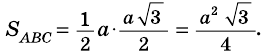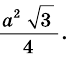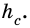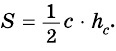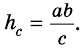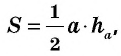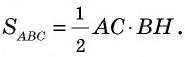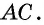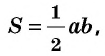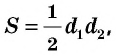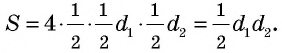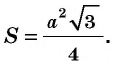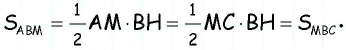Следствия из площади треугольника

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Площадь треугольника — определение и вычисление с примерами решения

Площадь треугольника:

Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть

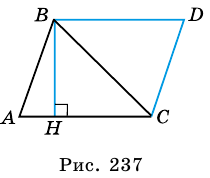
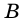
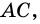
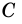
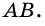
1) Проведем через вершину прямую, параллельную а через вершину — прямую, параллельную Получим параллелограмм

2) (по трем сторонам). Поэтому

откуда

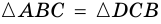
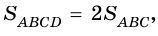
3) Так как 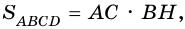то

В общем виде формулу площади 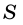треугольника можно записать так:

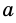
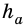
где — сторона треугольника, — высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

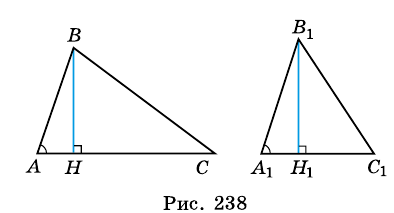
Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

Доказательство:

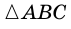
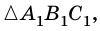
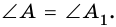
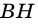
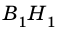
Рассмотрим и у которых Проведем высоты и (рис. 238).

2) (по острому углу), поэтому

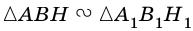
3) Имеем:

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна

Решение:

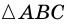
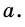
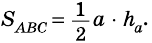
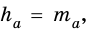
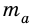
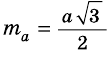
Пусть — равносторонний со стороной Тогда В равностороннем треугольнике где — медиана. Но (§ 18, задача 4), поэтому

Следовательно,

Ответ.

Пример:

Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

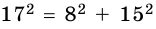
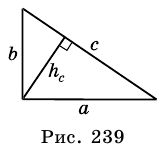
Так как (т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

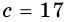
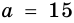
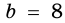
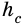
Пусть на рис. 239 изображен прямоугольный треугольник, у которого см -гипотенуза, и см — катеты, — высота. Найдем

Площадь этого треугольника можно найти

по формулам: 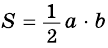или

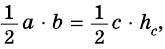
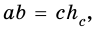
Тогда то есть откуда

Таким образом, имеем: 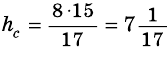(см).

Ответ. 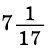см.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

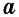
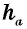
где — сторона треугольника, — проведенная к ней высота.

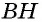
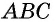
Пусть — высота треугольника (рис. 148). Докажем, что

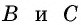
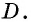
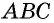
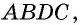
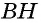
Проведем через вершины прямые, параллельные сторонам треугольника, и обозначим точку их пересечения Таким образом, мы «достроили» треугольник до параллелограмма в котором отрезок также является высотой, проведенной к стороне

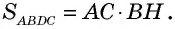
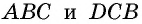
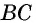
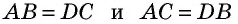
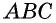
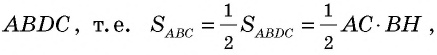
По формуле площади параллелограмма Треугольники равны по трем сторонам (у них сторона общая, как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника составляет половину площади параллелограмма что и требовалось доказать.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где 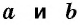— катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

Площадь ромба равна половине произведения его диагоналей:

где 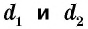— диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 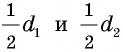(рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной 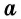вычисляется по формуле

Обоснуйте это следствие самостоятельно.

Опорная задача

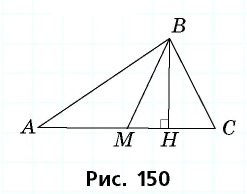
Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

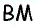
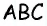
Пусть — медиана треугольника (рис. 150).

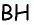
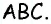
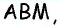
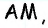
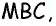
Проведем высоту треугольника Этот отрезок является одновременно высотой треугольника проведенной к стороне и высотой треугольника проведенной к стороне Учитывая равенство отрезков имеем:

Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Плоские и пространственные фигуры
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников
• Треугольники и окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Геометрия. 8 класс

Выведем формулу для вычисления площади треугольника и следствия из неё.
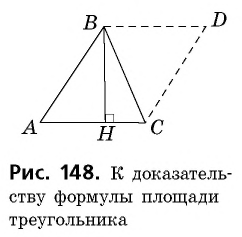
Одну из сторон треугольника будем называть основанием. Например, сторону AC. Тогда высотой треугольника будем считать ту, которая проведена к основанию.

Достроим треугольник ABC до параллелограмма. Площадь параллелограмма равна сумме площадей треугольников ABC и BCD.

S_ABC = 1/2 S_ABCD
S_ABC = 1/2 AB ∙ BC, но AB и BC – ab, поэтому
S_ABC = 1/2 ab, где a и b – катеты
Это первое следствие из теоремы о площади треугольника.
С другой стороны площадь прямоугольного треугольника равна половине произведения основания на высоту.

Пусть основанием является гипотенуза, а за высоту треугольника примем высоту, проведённую к гипотенузе.
S_ABC = 1/2 ch = 1/2 ab,
h = ab/c
Следствие второе:
Если высоты двух треугольников равны, то их площади относятся как основания.

Действительно, если h₁ = h₂ = h, то выражения для площадей примут вид
S_ABC = 1/2 AC ∙ hS_A1B1C1 = 1/2A₁C₁ ∙ h
S_ABC/S_A1B1C1 = (1/2 AC ∙ h)/(1/2 A₁C₁ ∙ h) = AC/A₁C₁
Тогда отношение площадей равно отношению оснований треугольников. Что и требовалось доказать.
Второе следствие помогает доказать утверждение:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Пусть ∠A = ∠A₁, тогда
S_ABC/S_A1B1C1 = (AB ∙ AC)/(A₁B₁ ∙ A₁C₁)
Знание формулы для вычисления площади прямоугольного треугольника позволяет вывести формулу для вычисления площади ромба, отличную от формулы площади параллелограмма.
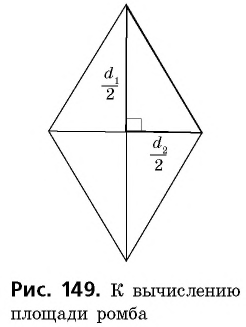
Известно, что диагонали ромба делят его на 4 равных прямоугольных треугольника. Поэтому площади этих треугольников равны. Значит, можно утверждать, что площадь ромба равна четырём площадям треугольника. Проведя дальнейшие рассуждения, получим, что площадь ромба равна половине произведения его диагоналей.

Видео:Площади треугольников с равным углом.Скачать

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции.

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формула для площади треугольника и следствия из неё

На данном уроке мы докажем формулу для площади треугольника и решим несколько задач на её применение.

Будем называть сторону – основанием, тогда – высота, опущенная к этой стороне (см. Рис. 1).

Рис. 1. Высота и основание

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Теорема о свойстве медианы треугольника

Площадь треугольника равна половине произведения его основания на высоту.

В формульном виде: .

Доказательство:

Рис. 2. Иллюстрация к теореме

Достроим треугольник до параллелограмма – см. Рис. 2.

(по трём сторонам: – общая, , – как противоположные стороны параллелограмма).

Из равенства треугольников следует равенство их площадей: . Получаем: . Воспользовавшись формулой для площади параллелограмма: .

Сформулируем несколько следствий из данной теоремы.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов (см. Рис. 3).

Рис. 3. Иллюстрация к следствию 1

.

Следствие 2

Если высоты двух треугольников равны, то их площади относятся как основания (см. Рис. 4).

Рис. 4. Иллюстрация к следствию 2

.

Теорема 2

Медиана треугольника разбивает его на два равновеликих треугольника (см. Рис. 5).

Доказательство:

Рис. 5. Иллюстрация к теореме

Пусть – треугольник, – медиана, – высота. Для треугольников – также является высотой. Запишем формулу для площади каждого из этих треугольников: , . Так как ( – медиана), то: . Значит, эти треугольники являются равновеликими.

Видео:Площадь треугольника, следствиеСкачать

Формула для площади ромба

Теорема 3

Площадь ромба равна половине произведения его диагоналей (см. Рис. 6).

В виде формулы: .

Доказательство:

Рис. 6. Иллюстрация к теореме

(по 3 сторонам: – общая, – свойства ромба). Из равенства треугольников следует равенство их площадей. Значит: . Но формулу для площади треугольника мы уже знаем: (т. к. , поэтому – высота треугольника ). Получаем следующее равенство: ( – свойство диагоналей ромба).

Видео:ГЕОМЕТРИЯ 8 класс : Площадь треугольникаСкачать

Свойство треугольников с равными углами

Теорема 4

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

В виде формулы: .

Доказательство:

Рис. 7. Иллюстрация к теореме

Совместим треугольники так, чтобы вершина совпала с вершиной , сторона лежала на прямой , а сторона лежала на прямой .

Рис. 8. Иллюстрация к теореме

Рассмотрим отношение площадей треугольников и . Эти треугольники имеют общую высоту, проведённую из вершины , поэтому, по следствию 2 из теоремы 1, их площади относятся как основания, то есть: .

Из аналогичных соображений: . Перемножив эти два равенства, получим: .

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Задачи на площадь треугольника и следствия из неё

Теперь решим несколько задач, используя доказанные формулы и свойства.

Задача 1

Площадь прямоугольного треугольника равна . Найдите катеты этого треугольника, если известно, что один из них составляет другого.

Решение

Пусть один из катетов равен , а второй – . Тогда площадь треугольника можно вычислить по формуле: . Но, по условию: . Подставив это выражение, получаем: . Откуда: .

Ответ: .

Задача 2

В треугольнике точка лежит на стороне , точка лежит на стороне . Кроме того: , , . Чему равна площадь треугольника (Рис. 9)?

Решение:

Рис. 9. Иллюстрация к задаче

Воспользуемся теоремой 4 для треугольников и ( – общий угол этих треугольников). Из этой теоремы следует, что: . Значит: .

Ответ: .

На этом уроке мы рассмотрели понятия площадей треугольника и ромба, вывели из них некоторые следствия. На следующем уроке мы научимся вычислять площадь трапеции.

🔍 Видео

Запомни: все формулы для площади треугольникаСкачать

Геометрия 8 Площадь треугольникаСкачать

100. Теорема о площади треугольникаСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Как найти площадь треугольника без формулы?Скачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

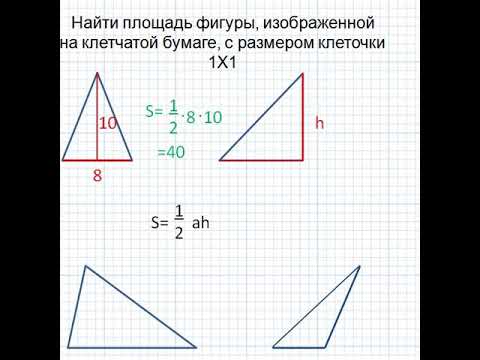
Площадь параллелограмма, треугольника, трапецииСкачать

Площади треугольникаСкачать