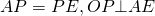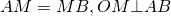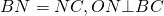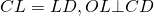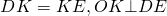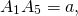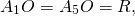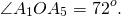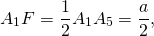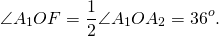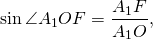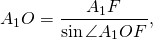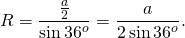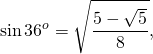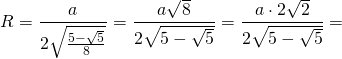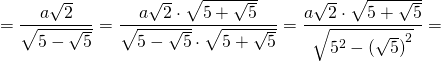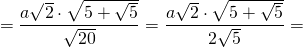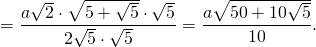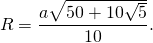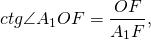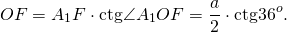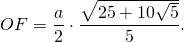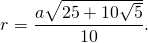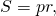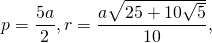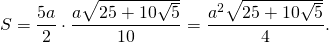Свойства окружности описанной около пятиугольника окружности (7 видео)

Описанная окружность

Что такое описанная окружность? Какими свойствами она обладает?

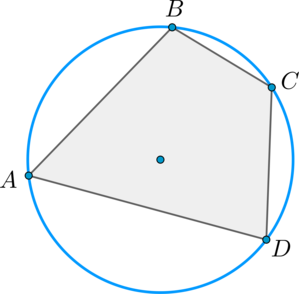
Описанная около выпуклого многоугольника окружность — это окружность, которая проходит через все вершины многоугольника.

Многоугольник, около которого описана окружность, называется вписанным.

В выпуклый многоугольник можно вписать окружность, если все серединные перпендикуляры к его сторонам пересекаются в одной точке.

Центр вписанной в многоугольник окружности — точка пересечения серединных перпендикуляров к его сторонам.

Центр описанной окружности равноудалён от вершин многоугольника.

Расстояние от центра до любой вершины многоугольника равно радиусу описанной окружности.

Окружность с центром в точке O и радиусом R описана около пятиугольника ABCDE.

ABCDE — вписанный пятиугольник.

O — точка пересечения серединных перпендикуляров к сторонам ABCD, то есть

Точка O равноудалена от вершин пятиугольника.

Расстояние от точки O до любой вершины равно радиусу:

Около любого правильного многоугольника можно описать окружность. В любой правильный многоугольник также можно вписать окружность. Центр вписанной и описанной окружности лежат в центре правильного многоугольника.

В отличие от вписанной окружности, общей формулы для нахождения радиуса описанной около многоугольника окружности нет. Радиус описанной окружности можно найти как радиус окружности, описанной около любого из треугольников, вершины которого являются вершинами описанного многоугольника.

Например, для описанного пятиугольника ABCDE радиус можно найти как радиус окружности, описанной около одного из треугольников ABC, ABD, ABE, BCD, BCE, ACD, ADE и т.д.

Формулы для нахождения радиуса описанной окружности существуют в частных случаях: для правильных многоугольников, треугольников, прямоугольника.

Содержание

2 Comments
Окружность: описанная около многоугольника
Как описать окружность вокруг пятиугольника
Как построить и нарисовать правильный пятиугольник по окружности
Параметры правильного пятиугольника
Построение пентагона
Интересные факты
Видео
Правильный пятиугольник — построение, свойства и формулы
Точное построение фигуры
Алгоритм Биона
Приближенные методы
Признаки и свойства
Расчет параметров
Условные обозначения
Соотношения и формулы
Правильный пятиугольник
Видео

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

2 Comments

Огромное спасибо за все статьи, что есть на этом сайте! Благодаря вам восполнила пробелы в теории, из-за которых не могла решить задачки, и теперь щёлкаю задания как орехи. Лучший сайт по геометрии!

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Окружность: описанная около многоугольника

Определение

Окружность (S) описана около многоугольника (P) , если все вершины многоугольника (P) лежат на окружности (S) .

В этом случае многоугольник (P) называется вписанным в окружность.

Определение

Серединный перпендикуляр к отрезку – это прямая, проходящая через середину данного отрезка перпендикулярно ему.

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство

Рассмотрим отрезок (AB) и серединный перпендикуляр (a) к нему. Докажем, что для любой точки (Xin a) выполнено: (AX=BX) .

Рассмотрим (triangle AXB) : отрезок (XO) является медианой и высотой, следовательно, (triangle AXB) – равнобедренный, следовательно, (AX=BX) .

Теорема

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство

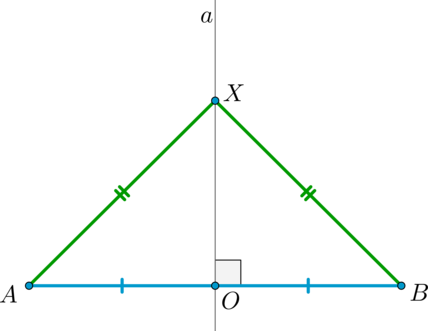
Рассмотрим (triangle ABC) . Проведем серединные перпендикуляры к сторонам (AB) и (AC) . Они пересекутся в точке (O) .

По предыдущей теореме для серединного перпендикуляра (C_1O) выполнено: (AO=BO) , а для (B_1O) — (AO=CO) . Следовательно, (BO=CO) . Значит, (triangle BOC) – равнобедренный, следовательно, высота (OA_1) , проведенная к основанию (BC) , будет также и медианой. Значит, (OA_1) – серединный перпендикуляр к отрезку (BC) .

Таким образом, все три серединных перпендикуляра пересеклись в одной точке (O) .

Следствие

Если точка равноудалена от концов отрезка, то она лежит на его серединном перпендикуляре.

Теорема

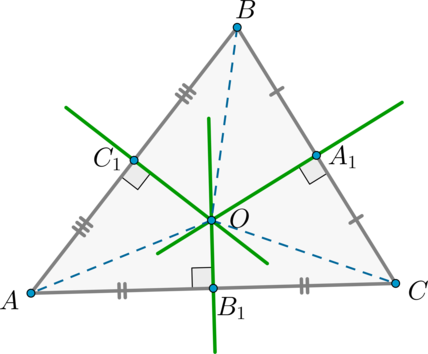
Около любого треугольника можно описать единственную окружность, причём центр описанной окружности есть точка пересечения серединных перпендикуляров к сторонам треугольника.

Доказательство

Из доказанной выше теоремы следует, что (AO=BO=CO) . Значит, все вершины треугольника равноудалены от точки (O) , следовательно, они лежат на одной окружности.

Такая окружность единственна. Допустим, что около (triangle ABC) можно описать еще одну окружность. Тогда ее центр должен совпасть с точкой (O) (т.к. это единственная точка, равноудаленная от вершин треугольника), а радиус должен быть равен расстоянию от центра до какой-то из вершин, т.е. (OA) . Т.к. у этих окружностей совпадают и центр, и радиус, то и эти окружности совпадают.

Теорема о площади вписанного треугольника

Если (a, b, c) – стороны треугольника, а (R) – радиус описанной около него окружности, то площадь треугольника [S_=dfrac]

Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Теорема синусов”.

Обозначим угол между сторонами (a) и (c) за (alpha) . Тогда (S_=frac12 accdot sin alpha) .

По теореме синусов (dfrac b=2R) , откуда (sin alpha=dfrac b) . Следовательно, (S_=dfrac) .

Теорема

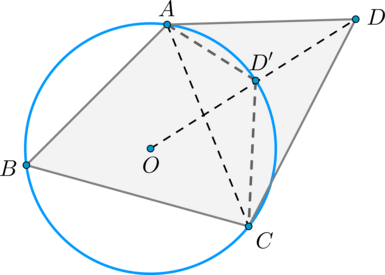
Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны (180^circ) .

Доказательство

Если около четырёхугольника (ABCD) можно описать окружность, то (buildrelsmileover + buildrelsmileover = 360^circ) , откуда (angle ABC + angle ADC = fracbuildrelsmileover + fracbuildrelsmileover = frac(buildrelsmileover + buildrelsmileover) = 180^circ) . Для углов (BCD) и (BAD) аналогично.

Опишем окружность около треугольника (ABC) . Пусть центр этой окружности – точка (O) . На прямой, проходящей через точки (O) и (D) отметим точку (D’) пересечения этой прямой и окружности. Предположим, что точки (D) и (D’) не совпали, тогда рассмотрим четырёхугольник (CD’AD) .

Углы (CD’A) и (CDA) дополняют угол (ABC) до (180^circ) ( (angle CDA) дополняет по условию, а (angle CD’A) по доказанному выше), следовательно, они равны, но тогда сумма углов четырёхугольника (AD’CD) больше (360^circ) , чего быть не может (сумма углов это четырёхугольника есть сумма углов двух треугольников), следовательно, точки (D) и (D’) совпадают.

Замечание. На рисунке точка (D) лежит вне круга, ограниченного окружностью, описанной около (triangle ABC) , однако, в случае, когда (D) лежит внутри, доказательство также остаётся верным.

Теорема

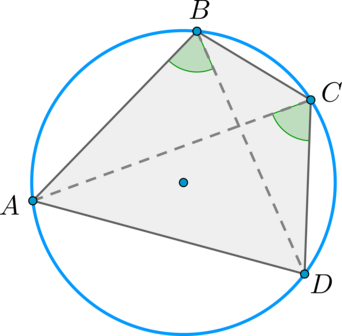
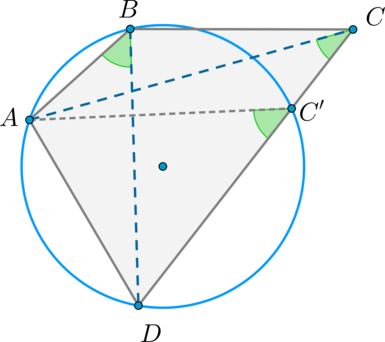
Около выпуклого четырехугольника (ABCD) можно описать окружность тогда и только тогда, когда (angle ABD=angle ACD) .

Доказательство

Необходимость. Если около (ABCD) описана окружность, то углы (angle ABD) и (angle ACD) – вписанные и опираются на одну дугу (buildrelsmileover) , следовательно, они равны.

Достаточность. Пусть (angle ABD=angle ACD=alpha) . Докажем, что около (ABCD) можно описать окружность.

Опишем окружность около (triangle ABD) . Пусть прямая (CD) пересекла эту окружность в точке (C’) . Тогда (angle ABD=angle AC’D Rightarrow angle AC’D=angle ACD) .

Следовательно, (angle CAD=angle C’AD=180^circ-angle ADC-angle AC’D) , то есть (triangle AC’D=triangle ACD) по общей стороне (AD) и двум прилежащим углам ( (angle C’AD=angle CAD) , (angle ADC’=angle ADC) – общий). Значит, (DC’=DC) , то есть точки (C’) и (C) совпадают.

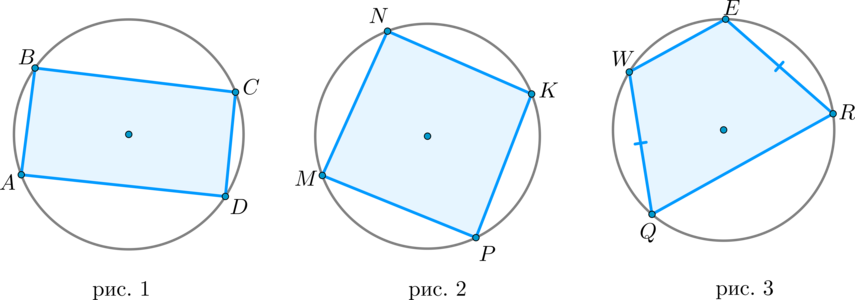
Теоремы

1. Если около параллелограмма описана окружность, то он – прямоугольник (рис. 1).

2. Если около ромба описана окружность, то он – квадрат (рис. 2).

3. Если около трапеции описана окружность, то она равнобедренная (рис. 3).

Верны и обратные утверждения: около прямоугольника, ромба и равнобедренной трапеции можно описать окружность, и притом только одну.

Доказательство

1) Пусть около параллелограмма (ABCD) описана окружность. Тогда суммы его противоположных углов равны (180^circ: quad angle A+angle C=180^circ) . Но в параллелограмме противоположные углы равны, т.к. (angle A=angle C) . Следовательно, (angle A=angle C=90^circ) . Значит, по определению (ABCD) – прямоугольник.

Обратное утверждение очевидно.

2) Пусть около ромба (MNKP) описана окружность. Аналогично предыдущему пункту (т.к. ромб является параллелограммом) доказывается, что (MNKP) – прямоугольник. Но все стороны этого прямоугольника равны (т.к. он ромб), значит (MNKP) – квадрат.

Обратное утверждение очевидно.

3) Пусть около трапеции (QWER) описана окружность. Тогда (angle Q+angle E=180^circ) . Но из определения трапеции следует, что (angle Q+angle W=180^circ) . Следовательно, (angle W=angle E) . Т.к. углы при основании (WE) трапеции равны, то она равнобедренная.

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Как описать окружность вокруг пятиугольника

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Видео:Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Правильный пятиугольник — построение, свойства и формулы

Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

Построить окружность с центром в некоторой точке О.

Провести два диаметра. Они должны пересекаться под прямым углом.

Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.

По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.

Отметить на отрезке OD точку А, которая делит его пополам.

Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.

Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.

Нарисовать окружность с радиусом, равным CV, из точки V.

Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).

Поставить иглу циркуля в точку F и провести окружность через Е.

Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.

Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).

Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Начертить окружность с центром в точке О и радиусом R.

Провести в ней диаметр АD.

Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.

Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.

Провести из точек С и Е прямые, перпендикулярные диаметру.

Точки пересечения прямых с окружностью обозначить F и G.

Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Приближенные методы

Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Начертить произвольную окружность с центром в точке О.

Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.

Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).

Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.

Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.

Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.

Углы равны по 108 градусов.

Центры вписанной и описанной окружностей совпадают.

Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.

Количество диагоналей соответствует 5.

Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.

Биссектрисы, проведенные через центр, равны.

Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.

Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

Сторона: a.

Радиус вписанной и описанной окружностей: r и R соответственно.

Площадь: S.

Периметр и полупериметр: P и p соответственно.

Диагональ: d.

Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).

Соотношения и формулы

После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:

a = 2r * tg(36).

a = 2R * sin(36).

a = R * [(5 — (5)^(1/2)) / 2]^(1/2).

Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

r = a / (2tg(36)).

r = a * [5^(1/2) * [5 + 2 * 5^(1/2)]^(1/2) / 10].

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:

R = a / (2sin(36)).

R = a * [10^(1/2) * [5 + 5^(1/2)]^(1/2) / 10] = (5^(1/2) — 1) * r.

Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

S = (5a^2 / 4) * ctg(36).

S = 5r^2 * tg(36).

S = 2,5 * R^2 * sin(72).

S = (5/12) * R * d.

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.

Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Правильный пятиугольник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.