Окружность симметрична относительно любого диаметра (2 видео)

Замечательное свойство окружности.

ОКРУЖНОСТЬ

i. 1. Окружность.Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.

ii. Свойства окружности.

1) Диаметр, перпендикулярный хорде, делит ее пополам.

2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.

3) Серединный перпендикуляр к хорде проходит через центр окружности.

5) Равные хорды удалены от центра окружности на равные расстояния.

6) Хорды окружности, удаленные от центра на равные расстояния, равны.

7) Окружность симметрична относительно любого своего диаметра.

8) Дуги окружности, заключенные между параллельными хордами, равны.

9) Из двух хорд больше та, которая менее удалена от центра.

10) Диаметр есть наибольшая хорда окружности.

Замечательное свойство окружности.

1) Геометрическое место точек M, из которых отрезок AB виден под прямым углом (ÐAMB =90 0 ), есть окружность с диаметром AB без точек A и B.

2) Геометрическое место точек M, из которых отрезок AB виден под острым углом (ÐAMB 0 ) есть внешность круга с диаметром АВ без точек прямой AB.

3) Геометрическое место точек M, из которых отрезок AB виден под тупым углом (ÐAMB > 90 0 ), есть внутренность круга с диаметром АВ без точек отрезка AB.

3.Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.

4.Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы.

5. Касательная к окружности.Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.

1) Касательная перпендикулярна радиусу, проведенному в точку касания.

2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности.

3) Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA=MB (Касательные, проведенные к окружности из одной точки, равны).

4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

5) Теорема о биссектрисах треугольника.Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

6.Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен .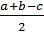

7.Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM=p−BC, где p — полупериметр треугольника.

8.Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.

9.Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M. Если ÐBAC = α, то ÐKLM = 90 0 − .

10.Даны окружности радиусов r и R (R > r). Расстояние между их центрами равно a (a>R + r). Тогда отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно a 2 −(R−r) 2 и a 2 −(R+r) 2 .

11.Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

12. Касающиеся окружности.Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания).

1) Точка касания двух окружностей лежит на их линии центров.

2) Окружности радиусов rиRс центрами O₁ и O₂ касаются внешним образом тогда и только тогда, когда R + r = O₁O₂.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Симметрия окружности

Есть ли симметрия в окружности? Сколько осей симметрии имеет окружность? Что является центром симметрии окружности?

Окружность имеет бесконечно много осей симметрии.

Осью симметрии окружности является любая прямая, содержащая диаметр окружности.

Проведём произвольный диаметр AB окружности.

Отметим на окружности произвольную точку X.

Из точки X проведём хорду, перпендикулярную диаметру.

Обозначим точки пересечения этой прямой с диаметром AB как P и X1.

Так как хорда перпендикулярна диаметру, то диаметр проходит через середину.

Следовательно, XP=X1P, а значит, точка X1 симметрична точке X относительно прямой, содержащей диаметр AB.

Имеем: точка, симметричная произвольной точке окружности относительно произвольного диаметра, также принадлежит окружности. Следовательно, любой диаметр окружности является её осью симметрии.

Что и требовалось доказать .

Окружность — центрально-симметричная фигура.

Осью симметрии окружности является её центр.

Отметим на окружности произвольную точку X.

Проведем через точку X диаметр XX1.

XO=X1O (как радиусы).

Таким образом, точка, симметричная произвольной точке окружности относительно её центра, также принадлежит окружности. Значит, окружность — центрально-симметричная фигура, а центр симметрии окружности — это центр окружности.

Видео:Радиус и диаметрСкачать

1.Укажите номера ВЕРНЫХ утверждений.
1)Середины перпендикулярны к сторонам треугольника пересекаются в одной точке.
2)Сумма двух сторон треугольника меньше третьей стороны.
3)Если две прямые параллельны третьей прямой, то они паралельны между собой.

2.Укажите номера ВЕРНЫХ утверждений.
1)Высота параллелограмма разбивает его на два равных треугольника.
2)В равнобедренной трапеции боковые сторны равны.
3)В ромбе противоположные углы равны.

3.Укажите номера НЕВЕРНЫХ утверждений.
1)В ромбе диагонали являются биссектрисами углов.
2)Окружность симметрична относительно любого своего диаметра.
3)Гипотенуза прямоугольного треугольника равна радиусу окружности, описанной около этого треугольника.

4.Укажите номера ВЕРНЫХ утверждений.
1)Площадь треугольника равна отношению произведения длин его сторон к радиусу описанной окружности.
2)Площадь трапеции равна произведению средней линии на высоту.
3)В прямоугольном треугольнике отношение катета к гипотенузе равна синусу угла, противолежащему этому катету.