Отношения между множествами выпуклых четырехугольников

Вопрос по математике:

(Задание 5)
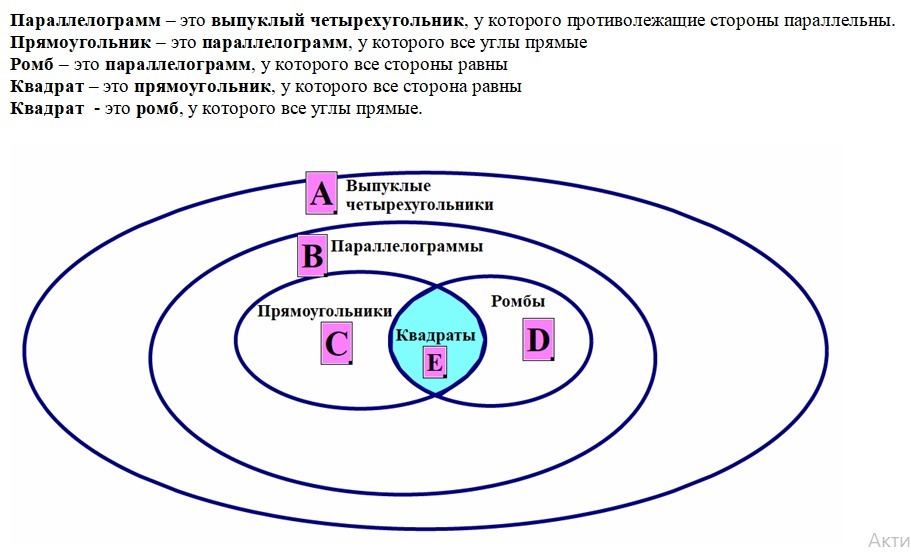
Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6. Покажите каждое из множеств

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Большой овал А, средний В, маленькие овалы С и Д, пересечение маленьких Е

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Математика. 4 класс. Отношения между множествами /06.10.2020/Скачать

(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?

Математика | 10 — 11 классы

(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6.

Покажите каждое из множеств.

Параллелограмм – это выпуклый четырехугольник, у которого противолежащие стороны параллельны.

Прямоугольник – это параллелограмм, у которого все углы прямые

Ромб – это параллелограмм, у которого все стороны равны

Квадрат – это прямоугольник, у которого все сторона равны

Квадрат — это ромб, у которого все углы прямые.

Видео:Математика. 5 класс. Отношения между множествами /10.03.2021/Скачать

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ.

Какие из этих множеств являются подмножествами других множеств?

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:Отношения объектов и их множеств | Информатика 6 класс #4 | ИнфоурокСкачать

Как может называться множество квадрат ромб круг?

Как может называться множество квадрат ромб круг?

Видео:Проверяем свойства отношенийСкачать

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты!

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Решите систему неравенств?

Решите систему неравенств.

На каком из рисунков изображено множество ее решений?

Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Какой четырехугольник не имеет оси симметрии?

Какой четырехугольник не имеет оси симметрии?

A) ромб б) прямоугольник в) параллелограмм г) квадрат.

Видео:Множества и операции над нимиСкачать

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция.

Видео:Математика. Отношения между множествами. 4 класс. Урок 25Скачать

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников.

Видео:Подмножество. 5 класс.Скачать

Запиши множество острых , множество прямых и множество тупых углов на рисунке ?

Запиши множество острых , множество прямых и множество тупых углов на рисунке .

Есть ли среди данных фигур прямоугольники .

Из букв входящих в каждой множество составь слова.

Видео:§3. Отношения объектов и их множеств. 5 клСкачать

Запиши множества острых, множество прямых и множество тупых углов на рисунке?

Запиши множества острых, множество прямых и множество тупых углов на рисунке.

Есть ли среди данных фигур прямоугольники?

На этой странице находится ответ на вопрос (Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

1) 43 / 56 — 11 / 24 = 52 / 1682) 1 6 / 7 : 52 / 168 = 63) 5 5 / 7 : 8 / 21 = 604) 60 + 6 = 66.

1)80 : 10 = 8 коробок с выключателями 2)120 : 10 = 12 коробок с розетками 3)12 — 8 = на 4 коробки с розетками больше, чем с выключателями.

Видео:№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

Характеристики понятия (содержание и объем) и связь между ними

Освоение понятий предполагает выделение свойств. Свойство — это то, что каким-то образом характеризует вещь и не требует для своего описания более одной вещи [1] .

Существенными свойствами понятия являются те свойства, без которых понятие (объект для понятия) не существует. При их помощи выделяются и обобщаются предметы интересующего нас множества. В литературе встречается и термин «существенные признаки». Но слово «признак» в школьном курсе математики имеет другой смысл, поэтому будем употреблять слово «свойство». Иногда под существенными свойствами объекта для понятия понимаются такие, каждый из которых, взятый отдельно, необходим, а взятые в совокупности достаточны для отделения данного понятия от остальных. Но в этой трактовке термин «существенные» скорее характеризует определенный набор, а не отдельные свойства, поэтому в дальнейшем под существенными свойствами будем понимать первую трактовку. Например, можно выделить следующие существенные свойства ромба. Быть параллелограммом, являться четырехугольником, иметь равные все стороны, иметь равные противоположные углы, диагонали в точке пересечения делятся пополам, диагонали лежат на биссектрисах углов ромба и т.д.

Конечно, таких свойств у объекта может быть много, поэтому часто обращаются к достаточному набору свойств. Достаточные свойства или, точнее, достаточный набор существенных свойств — набор существенных свойств, который позволяет однозначно выделить интересующее нас множество объектов из всех остальных.

Так, например, для ромба достаточный набор свойств могут образовывать свойства: быть параллелограммом и иметь все равные стороны. Другой достаточный набор: быть параллелограммом и иметь диагонали, делящие углы ромба пополам. Таких наборов может быть несколько. Они образуют либо определение понятия, либо его признаки.

В математике, как уже писали, чаще всего используется логический подход к трактовке понятия. С точки зрения логики любое понятие характеризуется термином, смыслом и знамением.

Термин (имя) — это языковое выражение, используемое для обозначения конкретных вещей.

Этими вещами могут быть предметы, свойства, отношения, процессы, явления и т.д. Предметы могут быть как материальными, так и идеальными, созданными воображением человека. Предмет, который обозначен термином, и является значением имени. Смысл, или концепт имени, — это способ, с помощью которого термин обозначает предмет [2] . Приведем пример, разъясняющий, что такое значение и смысл имени. Если взять термин понятия «Модест Петрович Мусоргский», то значением этого понятия будет конкретный человек, носивший это имя. А смыслов может быть несколько — «известный композитор», «создатель оперы “Хованщина”», «член кружка “Могучая кучка”». Если мы рассматриваем термин, то имеем в виду, во-первых, какой-то объект, который именуется этим термином, — значение имени, а во-вторых, то объективное содержание, которое выражается термином, — смысл термина. Термин «клетка» на уроке биологии и химии будет иметь смысл частицы живого организма, а на уроке математики обозначать частицу определенным образом разграфленной тетради. При этом для биологии и химии значение будет одно и то же, а вот смысл несколько отличаться, так как описываться на этих предметах клетка будет по-разному и будут изучаться ее свойства с разных сторон.

Математические понятия также характеризуются термином, смыслом и значением. Терминами понятий мы обозначаем математические объекты, которые изучает математика; значениями понятий являются идеи; смысл понятий может быть передан определением, системой аксиом, признаком, описанием свойств объектов, существенных для понятия. Один и тот же предмет может иметь множество разных имен. Например, языковые выражения «2 + 1»,

«V9», «2-», «корень уравнения х + 7 = 10» являются именами од- о

ного и того же предмета — числа 3. Выражения обозначают один и тот же предмет, т.е. имеют одно и то же значение, но смысл разный. Смысл имени « V9» состоит в том, что именуемое число может быть получено извлечением арифметического квадратного корня из числа 9, а смысл имени «корень уравнения х + 7 = 10» — именуемое число может быть получено путем решения простейшего уравнения х + 7 = 10.

Также один и тот же математический объект может иметь разные смыслы. Например, модуль числа имеет аналитический, геометрический смысл. Объект может иметь смысл (определить можно что угодно), но не иметь значение (может не существовать). И хотя в школе термины «смысл» и «значение» используются, но на

вопрос: «Имеет ли смысл и значение равенство ^9-у 2 = -5у 2 -16

разные учителя и ученики дают разные ответы. Конечно, смысл равенство имеет, так как имеют смысл выражения, стоящие в правой и левой части равенства (область определения уравнения как предиката), а вот значения нет.

Такую связь между термином, значением и смыслом можно изобразить в виде семантического треугольника (рис. 7.2). Треугольник называют треугольником Фреге.

Надо заметить, что связь между вершинами треугольника может быть неоднозначна. Это верно и для математики. Одному значению понятия может соответствовать не один термин, или смысл. Также одному термину может соответствовать несколько смыслов и даже значений, хотя математику отличает однозначность.

Например, в школьном курсе для термина «многоугольник» значением может быть часть плоскости, ограниченная замкнутой простой ломаной, и сама эта ломаная. Аналогичная ситуация с термином «угол». Поэтому при введении понятия желательно показать эту неоднозначность, а рассматривая понятие, договариваться, в каком смысле и значении его будем понимать.

Например, пересечением шестиугольника и пятиугольника на рисунке могут быть как две точки, так и четырехугольник в зависимости от смысла многоугольника (его определения) (рис. 7.3).

В методике обучения математике любое понятие характеризуется объемом и содержанием. Как эти характеристики понятия связаны с характеристиками понятия в логике?

Объем понятия — множество объектов, выделяемых и обобщаемых в понятии. Содержание понятия — совокупность свойств объектов, существенных для понятия. А значит, объем математического понятия — это и есть множество значений понятия (представителей, образов), а содержание отражает смысл понятия, которое описывается разными существенными для понятия свойствами. Но свойств может быть много, поэтому выделяют основное содержание — достаточный набор свойств, т.е. все те свойства, каждое из которых, взятое отдельно, необходимо, а взятые в совокупности достаточны для отличия данного понятия от остальных [3] .

На каждой новой ступени развития понятий возникают новые связи между понятиями. Так, сокращение содержания понятия С(С, з С₂) влечет за собой расширение его объема V(V _<a V₂). Эту операцию называют обобщением понятия. Например, если из содержания понятия «равносторонний треугольник» изъять свойство «равенство всех сторон», то множество треугольников, удовлетворяющих новому содержанию, станет «шире» — будет содержать множество всех равносторонних треугольников в качестве подмножества.

Расширение содержания понятия (С, с С₂) ведет к сужению его объема (Р, з V₂) и называется ограничением (специализацией) понятия. Пример такой операции — переход от понятия тождественных преобразований к понятию сокращения дробей. Рассмотрение отношений между выпуклыми четырехугольниками и окружностями привело к понятию вписанного в окружность четырехугольника. В результате в множестве выпуклых четырехугольников выделяется множество вписанных в окружность четырехугольников, которые характеризуются более сложным содержанием, но меньшим объемом по сравнению с множеством выпуклых четырехугольников.

Сформированность понятия характеризуется умением раскрыть все его существенные свойства в их (внутренних и внешних связях с другими понятиями) целостной совокупности, умением мыслить понятие в системе понятий. Например, рассмотрим следующую фразу: «Муха села на варенье». Обычно, слыша или произнося эту фразу, человек представляет живописную картинку. В понятиях же эту фразу можно трактовать следующим образом: «Элемент множества мух стал принадлежать множеству всех элементов, существенным свойством которых является “сидеть на варенье”». Как вы понимаете, вряд ли в обыденной жизни мы так мыслим. В обыденной жизни мы чаще оперируем предпонятиями.

Одно из основных действий изучения объекта и формирования понятия — действие определения.

📹 Видео

Практикум. Логические отношения между понятиями.Скачать

Множество. Элементы множества. 5 класс.Скачать

Математика. 4 класс. Закрепление. Отношения между множествами /08.10.2020/Скачать

Бинарные отношения. Как определить свойства?Скачать

Отношения между понятиями ЛОГИКА Урок 5Скачать

9 класс, 2 урок, Множества и операции над нимиСкачать

3.2 Бинарные отношения | Роман Попков | ИТМОСкачать

Пересечение множеств. Объединение множеств. 5 класс.Скачать