Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.
1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.
В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
 | 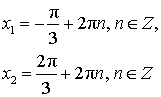 |
| tg x = – 1 | 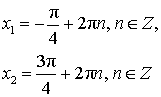 |
 |  |
| tg x = 0 |  |
 |  |
| tg x = 1 | 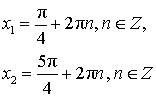 |
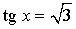 |  |
20(1). Вопрос: Определение производной, правила дифференцирования, примеры.
Ответ: Производная функции − одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место. Процесс нахождения производной называется дифференцированием. Обратная операция − восстановление функции по известной производной − называется интегрированием.
Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.
1. Вопрос: Аксиомы стереометрии. Следствия из аксиом (доказать одно из них).
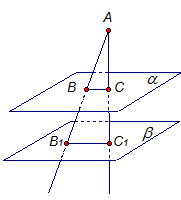
Ответ: А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
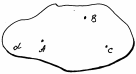 | А   В В   (точки А, В, С лежат в плоскости (точки А, В, С лежат в плоскости  ) С ) С   |
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
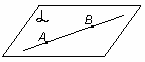 | АB   Прямая АВ лежит в плоскости Прямая АВ лежит в плоскости  |
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
 | а   = М Прямая а и плоскость = М Прямая а и плоскость  пересекаются в точке М. пересекаются в точке М. |
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
 |    = a = a  и и  пересекаются по прямой а. пересекаются по прямой а. |
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
1) Рассмотрим прямую a и точку A, которая не находится на этой прямой.
2) На прямой a выберем точки B и C.
3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B, Cи можно провести одну единственную плоскостьα.
4) Точки прямой a, B и C, лежат на плоскостиα, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
2. Вопрос: Теорема о параллельности трех прямых (формулировка и доказательство).
Ответ: Две прямые, параллельные третьей прямой, параллельны.
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным.
Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по теореме (Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.) это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
3. Вопрос: Параллельные прямые в пространстве(определение). Теорема о параллельных прямых.
Ответ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых: Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
4. Вопрос: Параллельность прямой и плоскости(определение). Признак параллельности прямой и плоскости.
Ответ: Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости:Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то прямая параллельна самой плоскости.
5. Вопрос: Расположение прямых в пространстве(виды). Признак скрещивающихся прямых.
Ответ:
Признак скрещивающихся прямых: Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
6. Вопрос: Углы с сонаправленными сторонами. Определение, теорема.
7. Вопрос: Признак параллельности двух плоскостей.
Ответ: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны.
8. Вопрос: Свойства параллельности плоскостей(доказать одно из них)
Ответ: Всего 3 свойства.
С1:Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Пусть даны параллельные плоскости 




Прямые а и b лежат в одной плоскости, а именно в плоскости γ. Докажем, что прямые а и b не пересекаются.
Если бы прямые а и b пересекались, то есть имели бы общую точку, то эта общая точка принадлежала бы двум плоскостям и 

Итак, прямые а и b параллельны, что и требовалось доказать.
С2: Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Пусть даны параллельные плоскости 

Две параллельные прямые АВ и СD образуют единственную плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости 

Прямые АВ и СD также параллельны (по условию). Значит, четырехугольник АВDС – параллелограмм, так как его противоположные стороны попарно параллельны.
Из свойств параллелограмма следует, что отрезки АВ и СD равны, что и требовалось доказать.
С3: Параллельные плоскости рассекают стороны угла на пропорциональные части.
Пусть нам даны параллельные плоскости 

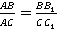
Параллельные плоскости 



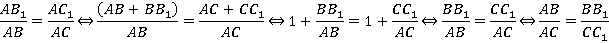
9. Вопрос: Тетраэдр и параллелепипед. Определения. Свойства параллелепипеда.
Ответ: Тетраэдр — поверхность, составленная из четырёх треугольников DАВ, DВС, DАС и АВС.
 | 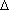 АВС, АВС, 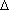 DАС, DАС, 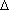 DВС, DВС, 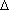 DАВ — грани. отрезки DА, DВ, АВ и т.д. — рёбра. точки А, В, С и т.д. — вершины. Рёбра АD и ВС — противоположные. Считается DАВ — грани. отрезки DА, DВ, АВ и т.д. — рёбра. точки А, В, С и т.д. — вершины. Рёбра АD и ВС — противоположные. Считается 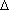 АВС — основание, остальные грани — боковые. АВС — основание, остальные грани — боковые. |
Параллелепипед. АВСDA1B1C1D1: поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1, лежащих в параллельных плоскостях и четырёх параллелограммов.
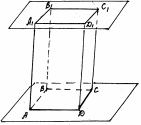 | все параллелограммы — грани, их стороны — рёбра, их вершины — вершины параллелепипеда. Считается: АВСD и A1B1C1D1 — основания, остальные грани — боковые. |
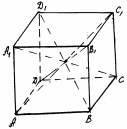 рис. 29 рис. 29 | Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: A1C, D1B, AC1, DB1. |
Свойства:
1. Противоположные грани параллелепипеда параллельны и равны.
Для любой пары противолежащих граней параллелепипеда имеем: соответствующие углы равны (например, 





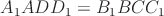
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
10. Вопрос: Признак перпендикулярности прямой и плоскости.
Ответ:Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
11. Вопрос: Теорема о трёх перпендикулярах.
Ответ: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
12. Вопрос: Признак перпендикулярности двух плоскостей.
Ответ: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
13. Вопрос: Призма. Основные элементы, Sбок, Sполн, Vпризмы.
Ответ: Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.
14. Вопрос: Пирамида. Основные элементы, Sбок, Sполн, Vпирамиды.
Ответ: Пирамида – многогранник, одна из граней которого (называется основанием) – произвольный многоугольник, а остальные грани соединяются в одной точке(вершине).
15. Вопрос: Усечённаяпирамида. Основные элементы, Sбок, Sполн.
Ответ: Усечённой пирамидой называется часть пирамиды, заключенная между её основанием и сечением пирамиды, параллельным основанию.
16. Вопрос: Двугранный угол. Градусная мера двугранного угла.
Ответ: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.Двугранный угол измеряется величиной своего линейного угла.Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
17. Вопрос: Прямоугольный параллелепипед. Свойства прямоугольного параллелепипеда (доказать одно из них).
Ответ: Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны.
Свойства прямоугольного параллелепипеда:
С1:В прямоугольном параллелепипеде все шесть граней прямоугольники.
С2: Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда — прямоугольники.
С3: Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.
АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.
Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD –линейныйуголданногодвугранногоугла. ∠А1АD = 90°, значит, двугранныйуголприребреАВравен 90°.
∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
18. Вопрос: Понятие многогранника. Виды. Примеры.
Ответ: Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
19. Вопрос: Правильная пирамида. Определение, Sбок.
Ответ: Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.
20. Вопрос: Симметрия в пространстве. Правильные многогранники.
Ответ: Точки А и A1 называются симметричными относительно точки О (центра симметрии), если О – середина отрезка AA1. Точка О симметрична сама себе.
Точки А и A1 называются симметричными относительно прямой а (ось симметрии) если прямая а проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка прямой a симметрична сама себе.
Точки А и A1 называются симметричными относительно плоскости a (плоскость симметрии) если плоскость a проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка плоскости a симметрична сама себе.
21. Вопрос: Уравнение сферы. Взаимное расположение сферы и плоскости.
Взаимное расположение сферы и плоскости:
1. Плоскость не пересекает сферу;
2. Плоскость касается сферы;
3. Плоскость пересекает сферу.
22. Вопрос: Касательная плоскость к сфере. Свойство с доказательством.
Ответ: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Свойство: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Доказательство: Из условия свойства следует, что данный радиус является перпендикуляром, проведенным из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку. Это и означает, что данная плоскость является касательной к сфере.
23. Вопрос: Цилиндр. Основные элементы, Sбок, Sполн, Vцилиндра.
Ответ: Цилиндр – тело, которое состоит из двух кругов, лежащих в параллельных плоскостях и всех отрезков, соединяющих соответствующие линии этих кругов.
Sбок=2πrh, r– радиус, h– высота;
24. Вопрос: Конус. Основные элементы, Sбок, Sполн, Vконуса.
Ответ: Конусом называется тело, которое состоит из круга, точки и всех отрезков, соединяющих эту точку с точкой круга. Круг называется основанием, а отрезки — образующими. Точка называется вершиной, а высота конуса перпендикуляр, проведённый из вершины конуса к основанию.
25. Вопрос:Шар и сфера, основные элементы, Sсферы, Vшара.
Ответ: Сфера – геометрическое место точек в пространстве, равноудалённых от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и её центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.
- Угол поворота, угол произвольной величины
- Поворот точки вокруг точки
- Полный оборот
- Угол поворота
- Направление поворота
- Величина угла поворота, угол произвольной величины
- Поворот фигуры вокруг точки на угол
- Урок «Поворот точки вокруг начала координат» методическая разработка по алгебре (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- 📸 Видео
Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Угол поворота, угол произвольной величины
Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Поворот точки вокруг точки
Центр поворота – точка, относительно которой осуществлен поворот.
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .
Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.
Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .
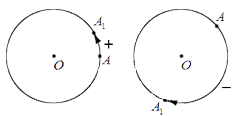
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:
Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Полный оборот
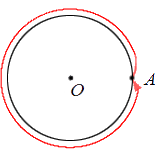
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .
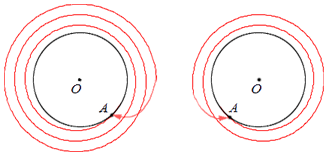
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:
В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.
Видео:поворот точки вокруг начала координат 10 класс алгебра и анализСкачать
Угол поворота
Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.
Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.
Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .
Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .
Разберем характеристики угла поворота подробнее.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Направление поворота
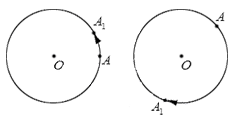
Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.
Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.
Видео:Поворот точки вокруг начала координатСкачать
Величина угла поворота, угол произвольной величины
Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.
Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;
Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.
Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.
Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.
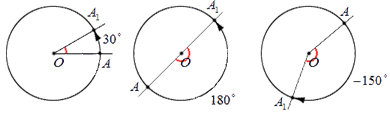
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :
Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:
Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.
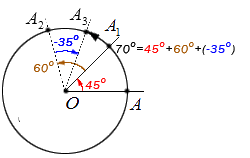
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:
Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .
По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .
Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.
В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.
При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .
Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Поворот фигуры вокруг точки на угол
Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).
Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .
Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Урок «Поворот точки вокруг начала координат»
методическая разработка по алгебре (10 класс) на тему
Второй урок темы «Тригонометрические функции» на 1-ом курсе в ОУ НПО. Тип урока: освоение нового материала. Понятия: угол, единичная окружность, координаты точки на окружности, поворот точки вокруг начала координат, определения синуса и косинуса — являются базовыми в разделе математики «Тригонометрия». Цель урока : освоить и закрепить основные понятия базового уровня.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Скачать:
| Вложение | Размер |
|---|---|
| povorot_tochki.pptx | 404.33 КБ |
| plan_otkrytogo_uroka.docx | 28.16 КБ |
Предварительный просмотр:
Видео:Как искать точки на тригонометрической окружности.Скачать

Подписи к слайдам:
Тригонометрические Функции Урок №2 Поворот точки вокруг начала координат Презентация к уроку Дроздова Наталия Геннадьевна преподаватель математики ГБОУ НПО ПЛ № 80
Проверка домашнего задания 1. Какая фигура называется углом ? 2. В чем измеряются углы? 3. Какие углы бывают, примеры их величин? 4. Какой угол принимают за угол в 1 0 ? 5 . Что такое угол в один радиан? 6 . Каково соотношение между радианом и градусом? 7 . Сколько радиан составляют 180 0 ?
Вариант 2 Вариант 1 Проверочная работа 180 0 = π
Ответы на проверочную работу Оценка за проверочную работу: 7-8 верных ответов — оценка « 3 » 9-10 верных ответов – оценка « 4 » 11-12 верных ответов – оценка « 5 »
Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р 1 1 -1 -1 точка Р — начало отсчета углов М α + α — α I четверть II четверть III четверть IV четверть — α
Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р точка Р — начало отсчета углов + α — α I четверть II четверть III четверть IV четверть α = 0 0 α = 90 0 α = 180 0 α = 270 0 α = 360 0
Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р точка Р — начало отсчета углов — α I четверть II четверть III четверть IV четверть α = 0 0 α = — 90 0 α = — 180 0 α = — 270 0 α = 360 0
Единичная окружность точка Р — начало отсчета углов Р О + α — α I четверть II четверть III четверть IV четверть α = 0 0 α = 90 0 α = 180 0 α = 270 0 α = 360 0 Задание устно: Определить четверть в которой лежит угол π 12 125 0 3 π 4 7 π 4 -45 0 7 π 8 — 300 0 -250 0 -150 0 210 0 330 0 390 0 460 0 -120 0
Координаты точки на единичной окружности О Р (1;0) I четверть II четверть III четверть IV четверть 0 0 90 0 = 180 0 = 270 0 = 360 0= А (0;1) В (-1;0) С (0;-1) Точке А (0,1) соответствую углы: 90 0 90 0 +360 0 90 0 +360 0 +360 0 +… 90 0 -360 0 90 0 -360 0 -360 0 -… Или в радианах :
Координаты точки на единичной окружности О Р (1;0) 0 0 90 0 = 180 0 = 270 0 = 360 0= А (0;1) В (-1;0) С (0;-1) М 1. Каждому углу соответствует единственная точка на окружности 2. Одной и той же точке на окружности соответствует бесконечное множество углов где к – целое число
Вариант 2 Вариант 1 Самостоятельная работа Найти координаты точки окружности, соответствующей углу: Записать все углы в радианах, соответствующие точке на окружности с координатами: 6. (0;-1) 7. (1;0) Найти координаты точки окружности, соответствующей углу: Записать все углы, соответствующие точке на окружности с координатами: 6. (-1;0) 7. (0;1)
Ответы на проверочную работу Сегодня на уроке я узнал ….. Сегодня на уроке я познакомился ……. Сегодня на уроке я повторил ……. Сегодня на уроке я научился……… Д/З: §22 стр .123 № 420
📸 Видео
§22 Поворот точки вокруг начала координатСкачать

Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать

Поворот точки вокруг начала координатСкачать

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Геометрия 9 класс (Урок№30 - Поворот.)Скачать

В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

Алгебра 10 класс Поворот точки вокруг начала координат СеминарСкачать

Поворот точки вокруг начала координатСкачать

радианная мера угла. Поворот точки вокруг начала координатСкачать

Радианная мера угла. 9 класс.Скачать