🌀 Открытие порядка в хаосе: погружение в нелинейную динамику и теорию хаоса

Нелинейная динамика и теория хаоса представляют собой увлекательные области математики и физики, которые изучают поведение систем, подчиняющихся сложным законам. Эти дисциплины раскрывают, как простые взаимодействия могут порождать неожиданно сложные явления и паттерны.

Теория хаоса, в частности, занимается системами, чье будущее состояние чрезвычайно чувствительно к начальным условиям, что делает долгосрочное предсказание их поведения практически невозможным. Это открытие имеет глубокие последствия для нашего понимания мира, от погодных систем до экономических рынков.

В этом разделе мы погрузимся в основы этих захватывающих тем, исследуя ключевые концепции и принципы, которые лежат в их основе. Мы узнаем, как нелинейность и хаос проявляются в самых разных областях, от природных явлений до технологических инноваций.

Видео:Как из хаоса рождается порядок? [Veritasium]Скачать

📈 Основы нелинейности: от простого к сложному

Нелинейность является ключевым элементом в понимании теории хаоса. Это концепция, которая описывает системы, чьё поведение не подчиняется прямолинейным причинно-следственным связям и предсказуемости. В таких системах малейшие изменения в начальных условиях могут привести к совершенно различным исходам.

Изучение нелинейных систем раскрывает, как простые правила могут порождать сложные и непредсказуемые паттерны. Это противоречит интуитивному пониманию, что сложное всегда строится из сложного. Напротив, нелинейные системы демонстрируют, что сложность может возникать из простоты.

Примеры нелинейности встречаются во многих областях, от погодных систем до человеческого поведения. Понимание нелинейности открывает новые горизонты для научных исследований и практических приложений, изменяя наш взгляд на мир и его явления.

Видео:Порядок и хаос. Силы, которые управляют ВселеннойСкачать

🔀 Что такое теория хаоса: понимание основ

Теория хаоса — это раздел математики, изучающий поведение определенных динамических систем, которые высокочувствительны к начальным условиям, явление, часто описываемое как “эффект бабочки”. Эта теория показывает, что даже в системах, которые кажутся полностью случайными, могут существовать неочевидные закономерности, порядок и структура.

Основы теории хаоса лежат в понимании, что малейшие изменения в начальных условиях могут привести к драматически различным исходам. Это противоречит интуитивному представлению о прямой пропорциональности причины и следствия и имеет множество приложений в научных и инженерных дисциплинах.

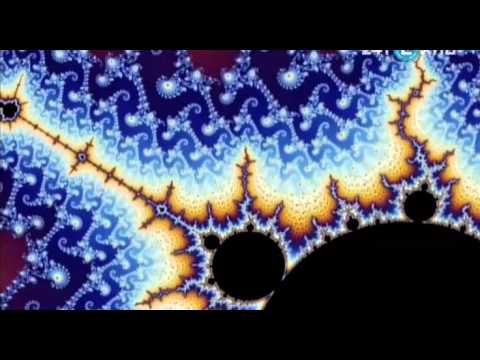
Важной концепцией в теории хаоса является фрактальная геометрия, которая описывает многие из этих кажущихся случайными структур. Фракталы — это самоподобные формы, которые повторяются на множестве масштабов и являются ключом к пониманию сложности многих естественных явлений.

Видео:Как из ХАОСА рождается порядок? Эффект бабочкиСкачать

🌪 Эффект бабочки: влияние мелких изменений на большие системы

Концепция, известная как «эффект бабочки», иллюстрирует, как незначительные колебания в одной части системы могут вызвать неожиданные и обширные последствия в другой. Эта идея, зародившаяся в рамках теории хаоса, подчеркивает сложность предсказания поведения систем, которые реагируют на малейшие внешние воздействия.

Примером служит метеорологическая система, где простое биение крыльев бабочки может быть катализатором цепной реакции, в результате которой формируется ураган в другой части света. Хотя это представление является упрощенным, оно наглядно демонстрирует основной принцип: в высоко связанных и нелинейных системах начальные условия играют решающую роль в определении дальнейших состояний системы.

Осознание этого эффекта подталкивает к более глубокому изучению нелинейных систем и их поведения. От экологических систем и климатических изменений до экономики и социальных наук — влияние мелких изменений может быть обнаружено почти в каждой области исследования. Это понимание заставляет ученых и исследователей подходить к анализу и моделированию данных с большой осторожностью, учитывая возможность широкомасштабных изменений, вызванных первоначально незначительными факторами.

Таким образом, «эффект бабочки» не только меняет наше восприятие причинно-следственных связей в сложных системах, но и предлагает уникальный взгляд на мир, в котором мы живем, подчеркивая важность мельчайших деталей в формировании общей картины.

Видео:15x4 - 15 минут о теории хаосаСкачать

📊 Аттракторы и странные аттракторы: центры хаоса и порядка

Аттракторы в теории хаоса — это состояния, к которым система стремится со временем. Они могут быть простыми, как точка равновесия, или сложными, как странные аттракторы, которые характеризуются фрактальной структурой и предсказуемой непредсказуемостью.

Странные аттракторы — это математические конструкции, которые, несмотря на кажущийся хаос, следуют определённым закономерностям. Они являются примером того, как в системах с нелинейной динамикой могут возникать порядок и структура из кажущегося беспорядка.

Изучение аттракторов помогает учёным понять, как системы могут развиваться и поддерживать стабильность даже в условиях кажущегося хаоса. Это открывает новые перспективы для прогнозирования поведения сложных систем в различных областях, от метеорологии до экономики.

Видео:Теория Хаоса: чем хаос отличается от случайности?Скачать

🌐 Примеры нелинейной динамики в природе и науке

Природа и научные исследования предлагают обилие примеров, демонстрирующих принципы нелинейной динамики. Один из самых известных примеров — погодные условия. Поведение атмосферы, особенно формирование ураганов и торнадо, наглядно показывает, как малейшие изменения в начальных условиях могут привести к радикально разным исходам.

Ещё один поразительный пример можно наблюдать в популяциях животных. Динамика численности определённого вида подчиняется нелинейным законам, где простое увеличение числа особей может привести к неожиданным всплескам или падениям из-за сложных взаимодействий с окружающей средой и другими видами.

В области медицины нелинейная динамика помогает понять распространение инфекционных заболеваний. Модели, основанные на нелинейности, применяются для прогнозирования эпидемий, позволяя учёным и медикам разрабатывать стратегии контроля и предотвращения широкомасштабных вспышек.

Также стоит упомянуть кардиологию, где исследования сердечного ритма выявили нелинейные паттерны в его работе. Эти открытия не только углубили наше понимание работы сердца, но и привели к разработке новых методов диагностики и лечения сердечных заболеваний.

В физике и химии нелинейная динамика проявляется в таких явлениях, как турбулентность жидкостей, химические осцилляции и паттерны реакций Белоусова-Жаботинского. Эти процессы иллюстрируют, как нелинейные системы могут порождать сложные и порой предсказуемые структуры из простых начальных условий.

В целом, примеры нелинейной динамики в природе и науке подчёркивают глубину и сложность мира вокруг нас, демонстрируя, что даже в кажущемся хаосе можно обнаружить порядок и структуру.

Видео:Игры хаоса. Фракталы [Numberphile на русском]Скачать

🔗 Обратная связь и самоорганизация: ключевые механизмы

Обратная связь и самоорганизация являются фундаментальными концепциями, лежащими в основе многих нелинейных систем и теории хаоса. Эти процессы объясняют, как системы могут развиваться и поддерживать порядок даже в условиях кажущегося беспорядка.

Обратная связь возникает, когда система регулирует себя посредством возвращения информации о своих предыдущих состояниях. Это может привести к усилению или затуханию определенных паттернов поведения. Самоорганизация же относится к способности системы формировать структурированные, упорядоченные конфигурации без внешнего управления.

Эти механизмы имеют решающее значение для понимания сложных систем, таких как климатические изменения, экономические рынки и даже развитие живых организмов. Они позволяют системам адаптироваться и эволюционировать, поддерживая динамическое равновесие между устойчивостью и изменчивостью.

Видео:Хаос. Эффект бабочки и проблема трёх тел [Veritasium]Скачать

🔢 Математические модели хаоса: фракталы, логистическая карта и другие

Изучение хаоса и нелинейности раскрывается через разнообразные математические подходы, среди которых выделяются фракталы и логистическая карта. Эти методы позволяют глубже понять, как из простых правил могут возникать сложные и непредсказуемые структуры.

Фракталы представляют собой удивительные геометрические формы, отличающиеся самоподобием на разных масштабах. Известно, что они не только встречаются в математической теории, но и широко распространены в природе, например, в формах береговых линий, растений и кровеносных систем. Основополагающая особенность фракталов — их способность демонстрировать бесконечную сложность, возникающую из относительно простых итеративных процессов.

Логистическая карта, ещё один фундаментальный инструмент в изучении динамики хаоса, используется для моделирования изменений в популяциях. Эта модель иллюстрирует, как даже простые нелинейные системы могут проявлять сложное и хаотичное поведение. Зависимость между текущим состоянием системы и её будущим показывает, что небольшие различия в начальных условиях приводят к значительно разным результатам, что является эхом эффекта бабочки в теории хаоса.

Эти модели, включая фракталы и логистическую карту, обогащают понимание хаотических систем, позволяя учёным предсказывать и анализировать сложные явления в различных областях — от экологии до экономики. Исследования в этой сфере продолжают раскрывать удивительные взаимосвязи между порядком и хаосом, демонстрируя красоту и сложность математической природы нашего мира.

Видео:BBC Порядок и Хаос История энергии 2012Скачать

🔍 Фрактальная геометрия в искусстве и природе: визуальное изучение

Фрактальная геометрия представляет собой удивительное переплетение науки и эстетики. Она находит своё отражение как в естественных образованиях, так и в художественных произведениях, демонстрируя, что математика может быть исключительно красивой.

В природе фракталы встречаются повсеместно: от ветвления деревьев до формирования снежинок. Каждый из этих объектов несёт в себе характерные черты фракталов — самоподобие и сложную структуру, возникающую из простых повторяющихся процессов.

В искусстве фрактальная геометрия используется для создания завораживающих образов и узоров. Художники и дизайнеры часто обращаются к фракталам за вдохновением, создавая произведения, которые отражают бесконечную сложность и красоту.

Видео:Порядок из хаоса [Numberphile]Скачать

🎲 Случайность vs Детерминированность: размышления о предсказуемости

В центре дискуссий о нелинейной динамике и теории хаоса находится диалог между случайностью и детерминированностью. Этот разговор касается основных принципов, определяющих, насколько точно мы можем предсказывать будущее событий в сложных системах. С одной стороны, детерминированность утверждает, что при наличии полных знаний о системе и её начальных условиях можно точно предсказать её будущее. С другой стороны, концепция случайности предполагает, что некоторые события происходят без явной причины, делая будущее непредсказуемым.

Основное отличие между этими двумя подходами лежит в понимании, как информация и начальные условия влияют на динамику системы. В мире, где теория хаоса играет ключевую роль, даже самые незначительные изменения в начальных условиях могут привести к радикально различным исходам, подчеркивая ограничения детерминированного подхода к предсказанию.

Эта дискуссия раскрывает глубокие философские вопросы о природе реальности и наших способностях к пониманию и предсказанию мира вокруг нас. В научных исследованиях и практических приложениях эти концепции вынуждают исследователей подходить к моделированию и анализу данных с учетом внутренней неопределенности и потенциальной непредсказуемости.

В итоге, размышление о взаимодействии между случайностью и детерминированностью в нелинейной динамике и теории хаоса предлагает более глубокое понимание ограничений и возможностей наших предсказательных моделей, а также о том, как мы воспринимаем сложность и неопределенность в мире, который нас окружает.

Видео:Тайна теории хаоса раскрыта!Скачать

💡 Применение теории хаоса в реальном мире: от экономики до медицины

Теория хаоса находит свое применение в самых разнообразных сферах жизни. В экономике, например, она помогает анализировать непредсказуемые рыночные тренды и финансовые кризисы. В медицине теория хаоса используется для понимания сложных биологических систем и распространения заболеваний.

Одним из ключевых аспектов теории хаоса является идея, что малейшие изменения в начальных условиях могут привести к значительным и непредсказуемым результатам. Это осознание приводит к более глубокому пониманию динамических систем и способствует разработке новых стратегий для управления сложностью и неопределенностью.

В экономических системах теория хаоса помогает распознавать сложные паттерны, которые могут указывать на нестабильность рынка или предстоящие изменения. В медицине она может пролить свет на то, как заболевания распространяются в популяциях и как могут развиваться эпидемии, что критически важно для предотвращения и контроля болезней.

Видео:93. Правило 2. Порядок и хаосСкачать

👩‍🔬 Влиятельные фигуры в области нелинейной динамики и теории хаоса

Исследование нелинейной динамики и теории хаоса невозможно без упоминания замечательных умов, чьи работы оказали значительное влияние на эти области. Один из таких учёных — Эдвард Лоренц, математик и метеоролог, чьё открытие эффекта бабочки стало краеугольным камнем теории хаоса. Его работа подчеркнула, как малейшие изменения в начальных условиях системы могут привести к драматически разным результатам на большом временном промежутке.

Бенуа Мандельброт, ещё один выдающийся учёный, известен своим вкладом в развитие фрактальной геометрии — концепции, которая нашла применение во многих областях науки, от математики до экономики. Мандельброт исследовал, как фракталы могут описывать сложные структуры и процессы в природе, подчёркивая самоподобие и масштабную инвариантность.

Митчел Фейгенбаум, знаменитый своим открытием констант Фейгенбаума, сделал ключевой вклад в понимание перехода от порядка к хаосу в динамических системах. Его работы предоставили математическую основу для изучения периодичности и хаоса, раскрывая универсальные свойства нелинейных систем.

Хенри Пуанкаре, французский математик, теоретический физик и философ науки, считается одним из основоположников теории динамических систем. Его исследования в области математической физики и топологии легли в основу многих современных концепций в нелинейной динамике и теории хаоса.

Эти учёные, вместе с многими другими талантливыми исследователями, внесли неоценимый вклад в развитие понимания сложных систем, которые формируют мир вокруг нас. Их открытия и теории продолжают вдохновлять новые поколения учёных на поиск ответов на самые загадочные вопросы природы и науки.

Видео:08 В Хаосе рождается порядок, а в порядке рождается ХаосСкачать

📚 Как начать изучение нелинейной динамики и теории хаоса: ресурсы и курсы

Погружение в мир нелинейной динамики и теории хаоса начинается с осознания того, что в основе кажущегося беспорядка лежат закономерности. Для тех, кто стремится раскрыть эти закономерности, существует множество ресурсов и курсов.

Начать стоит с базовых математических принципов, которые лежат в основе теории. Онлайн-курсы, академические лекции и специализированные учебники могут стать надёжным фундаментом для новичков. Многие университеты предлагают открытые курсы, доступные для самостоятельного изучения.

Для практического применения знаний можно использовать программное обеспечение для моделирования нелинейных систем. Это позволит визуализировать аттракторы, фракталы и другие явления, связанные с теорией хаоса.

Видео:Арестович: Семинар "Теория Хаоса" 24 июня. @ApeironSchoolСкачать

🔄 Влияние теории хаоса на современную науку и философию

Теория хаоса оказала значительное влияние на различные области знаний, переосмыслив наши представления о сложности и предсказуемости. В науке это понятие привнесло новые методы в анализ сложных систем, от атмосферных циркуляций до квантовых вычислений.

В философии теория хаоса стимулировала дебаты о свободе воли, предопределенности и сущности реальности. Она предложила альтернативный взгляд на каузальность и связь между причиной и следствием, вызывая переосмысление традиционных философских концепций.

Современная наука использует принципы теории хаоса для разработки новых технологий и решения сложных задач. Это включает в себя моделирование климата, управление трафиком и даже разработку новых лекарственных препаратов.

📺 Видео

"Хаос", теория "Хаоса", она работает?Скачать

ДФ Фракталы. Порядок в хаосеСкачать

Алексей Арестович о теории хаоса.Скачать

Хаос не хаотичен: Фракталы, Аттракторы, Фрактал Мандельброта и Главный Секрет Порядка ВселеннойСкачать

ХАОС И ПОРЯДОКСкачать

Хаос и порядок в жизниСкачать

Порядок против хаоса: Джордан ПитерсонСкачать