T найти ребра треугольника (7 видео) | Курс школьной геометрии

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Три стороны треугольника.
Две стороны треугольника и угол между ними.
Две стороны и угол противостоящий к одному из этих сторон треугольника.
Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Содержание

Решение треугольника по трем сторонам
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по стороне и любым двум углам
Решить треугольник Онлайн по координатам
Калькулятор сторон и углов треугольника
Как решить треугольник
Примеры решений практических задач
Треугольники
Свойства треугольников
Радиус вписанной окружности
Радиус описанной окружности
🎦 Видео

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

И, наконец, находим угол C:

Видео:Найдите третью сторону треугольникаСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее, из формулы

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

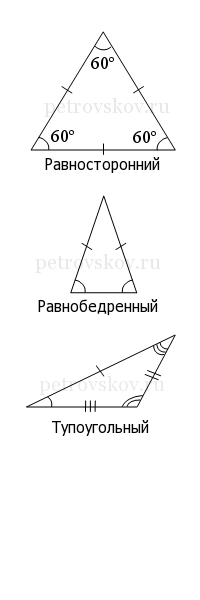
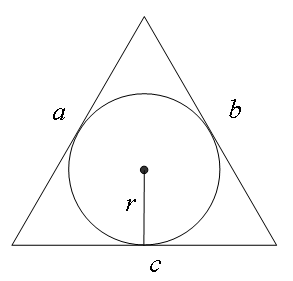
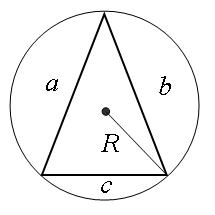
A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Видео:Уравнения стороны треугольника и медианыСкачать

Калькулятор сторон и углов треугольника

Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,

A = CAB, B = ABC, C = BCA − углы, противолежащие сторонам a, b, c соответственно.

Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».

Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.

Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Как решить треугольник

Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.

Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.

Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.

В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.

Видео:Найдите сторону треугольника на рисункеСкачать

Примеры решений практических задач

1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».

В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см 2 ;
Высота h_a = 7,9664 см;
Высота h_b = 11,9496 см;
Высота h_c = 6,9273 см;
Медиана m_a = 9,5513 см;
Медиана m_b = 12,2958 см;
Медиана m_c = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.

2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».

Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см 2 ;
Высота h_a = 2,9046 см;
Высота h_b = 1,9364 см;
Высота h_c = 1,4523 см;
Медиана m_a = 3,3912 см;
Медиана m_b = 2,7839 см;
Медиана m_c = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.

Таким образом, были найдены все углы треугольника.

3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см 2 ;
Высота h_a = 1,8314 см;
Высота h_b = 3,5355 см;
Высота h_c = 2,5019 см;
Медиана m_a = 1,9488 см;
Медиана m_b = 4,1857 см;
Медиана m_c = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Треугольники

Треугольник – многоугольник, который состоит из трех точек, соединенных тремя отрезками. Три точки в этом многоугольнике – вершины треугольника, а отрезки – стороны или ребра треугольника. На рисунке показан треугольник ΔABC, где A, B, C – его вершины, а AB, BC, AC – его стороны. Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.

Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.

Стороны треугольника

Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам.

Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.

Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.

Углы треугольника

Треугольники бывают остроугольными, тупоугольными и прямоугольными.

Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.

Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.

Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Свойства треугольников

В треугольнике только один угол может быть больше 90 градусов.

В треугольнике сумма углов равна 180 градусам.

Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.

Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Радиус вписанной окружности

Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника.

Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.

Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.

Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Радиус описанной окружности

Окружность, описанная около треугольника, проходит через 3 вершины треугольника.

Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.

🎦 Видео

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,Скачать

Почти никто не решил ➜ Найдите сторону треугольникаСкачать

Найдите стороны треугольникаСкачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Задача про стороны треугольника. Геометрия 7 класс.Скачать