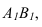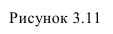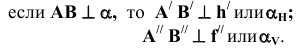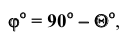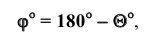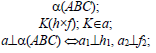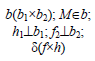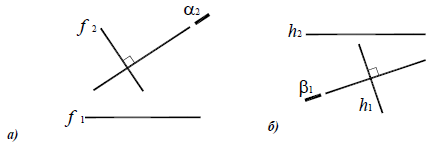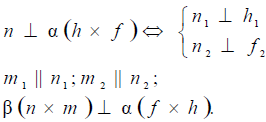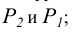Расстояние от точки до плоскости заданной параллельными прямыми начертательная геометрия

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.

1. Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.
2. Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.

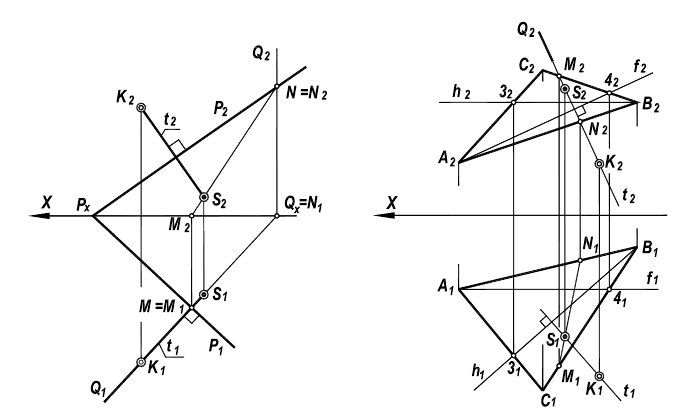
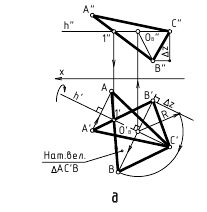
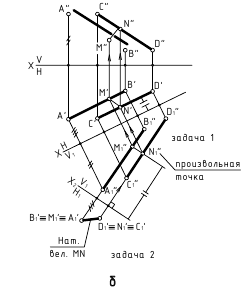
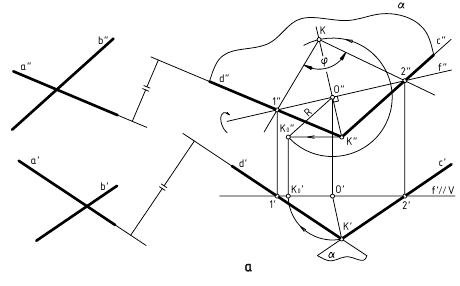
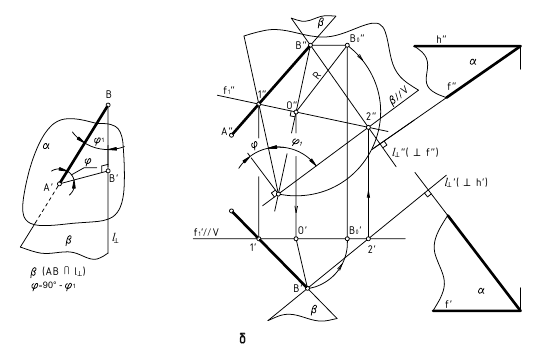
Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.

• Через вершину B» треугольника A»B»C» проводим проекцию h» горизонтали h. По линиям связи находим h’.
• Переводим ABC в проецирующее положение. Для этого перпендикулярно h вводим новую фронтальную плоскость П₄. Проецируем на неё точку N и треугольник ABC.
• Из точки N»₁ проводим N»₁M»₁ ⊥ A»₁C»₁. Длина отрезка N»₁M»₁ – искомое расстояние между плоскостью треугольника ABC и точкой N.

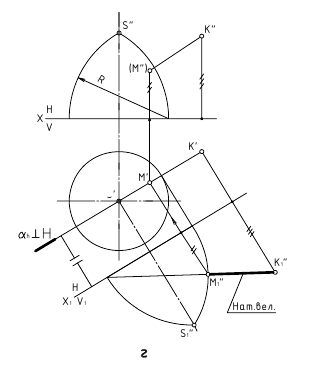
Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами. В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h_0β.

• Переводим плоскость β в проецирующее положение. Для этого перпендикулярно следу h_0β вводим дополнительную фронтальную плоскость П₄. На прямой f_0β берем произвольную точку E, определяем её проекции E», E’ и E»₁. Через E»₁ и X_0α1 проводим прямую f_0β1, которая является следом плоскости β на П₄. По линии связи определяем проекцию K»₁ точки K.
• Из K»₁ проводим перпендикуляр K»₁M»₁ в направлении прямой f_0β1. Длина отрезка K»₁M»₁ – величина искомого расстояния от K до β.

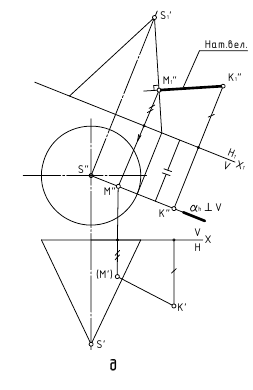
Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.

Видео:Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Решение метрических задач в начертательной геометрии с примерами

Содержание:

К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.

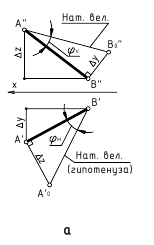
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым — разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция

Если необходимо определить угол наклона отрезка АВ к плоскости то построение прямоугольного треугольника ведется на фронтальной проекции.

Видео:Расстояние от точки до плоскостиСкачать

Решение метрических задач методами преобразовании проекций

Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций

Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.

Приведем некоторые из них.

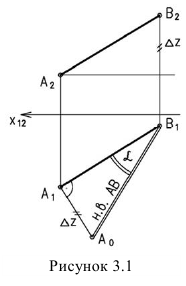
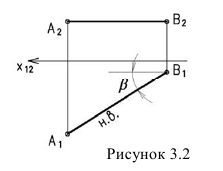
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).

— угол наклона к плоскости

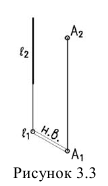
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).

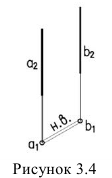
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).

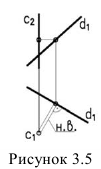
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).

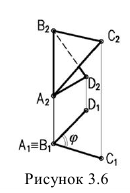
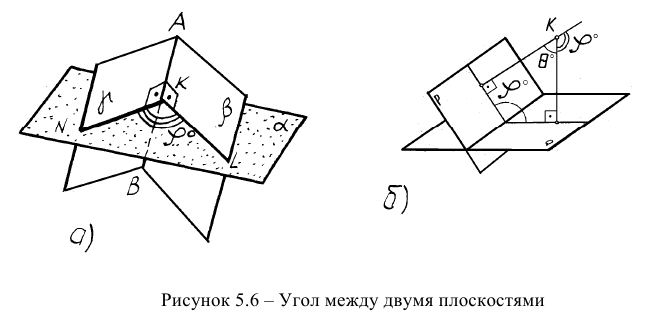
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).

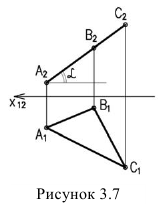
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)

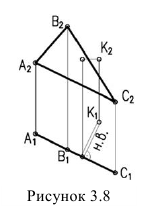
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)

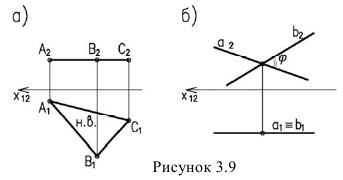
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)

Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.

Для такого перехода и служат способы преобразования проекций.

Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.

Четыре основных задачи преобразовании проекций

Этими способами решаются четыре основные задачи:

• Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
• Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
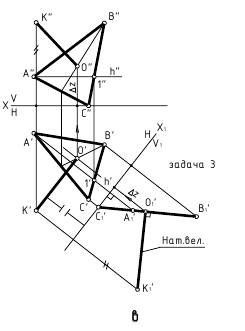
• Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
• Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)

Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций

Способ вращения

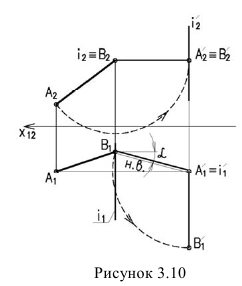
Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая — но прямой параллельной оси проекций.

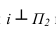
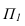
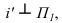
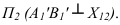
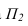
На рисунке 3.10 вокруг осивращаем отрезок ЛВ до положения параллельного плоскости(1 задача). Далее вращением вокруг осиполученный отрезок до положения перпендикулярного плоскости На отрезок с проецируется в точку

Способ плоскопараллельного перемещения

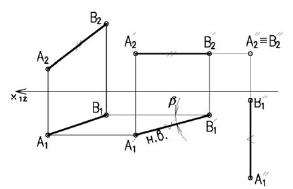
Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.

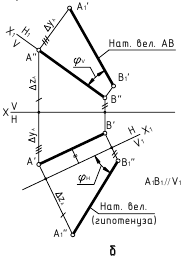
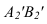
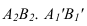
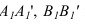
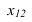
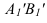
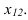
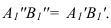
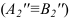
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом должно быть равно по величина находим в пересечении вертикальных линий связи и линий параллельных оси (1 задача). Далее отрезок перемещаем до положения перпендикулярного оси При этом На фронтальной проекции отрезок с проецируется в точку (2 задача).

Способ замены плоскостей проекций

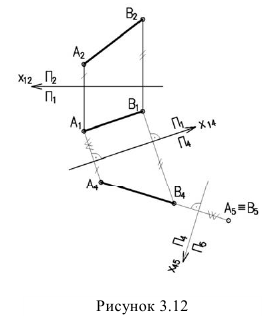
Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.

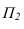
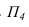
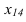
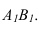
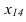
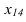
На рисунке 3.12 произведена первая замена плоскость заменена на новую фронтальную плоскость параллельную прямой АВ. При этом новая ось проводится параллельно проекции Линии связи проводятся перпендикулярно оси и на них от откладываются координаты z точек А и В (1 задача).

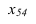
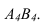
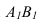
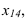
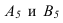
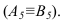
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось перпендикулярно проекции. Т.к. параллельна оси , расстояние до проекций будет одинаковое и прямая спроецируется в точку (2 задача)

Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций

Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.

Способ плоскопараллельного перемещения

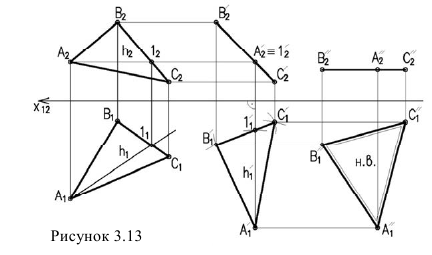
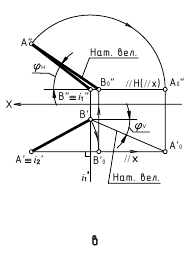
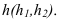
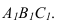
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь Далее располагаем перпендикулярно оси Откладываем на ней отрезок и циркулем строим треугольник равный по величине На фронтальной проекции треугольник проецируется в линию (3 задача).

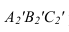
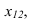
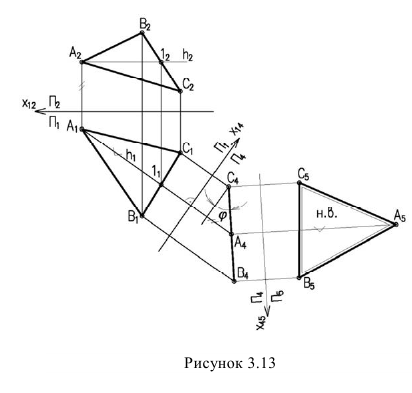
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию расположить параллельно оси при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)

Способ замены плоскостей проекций

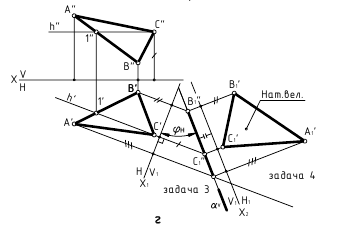
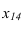
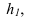
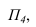
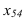
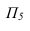
При решении задачи методом замены (рисунок 3.14) новую ось проводим перпендикулярно горизонтали тогда на новую фронтальную плоскость треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось провести параллельно плоскости На новую плоскость треугольник спроецируется в натуральную величину.

Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.

Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Метрические задачи

Метрические задачи — это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.

Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.

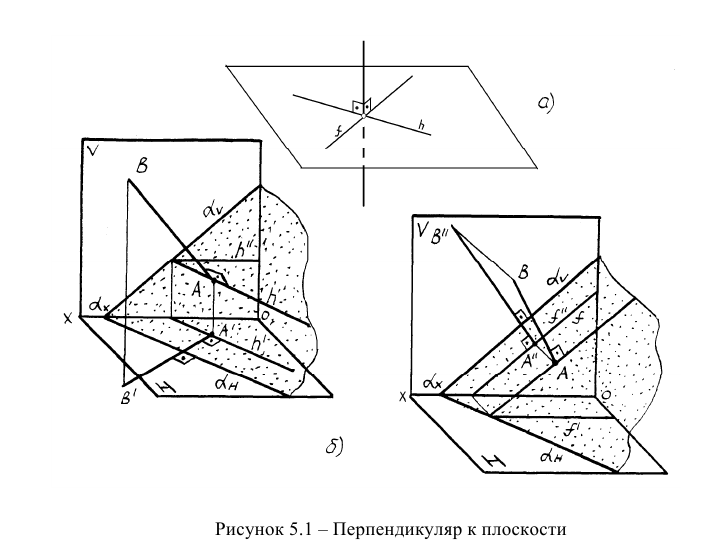
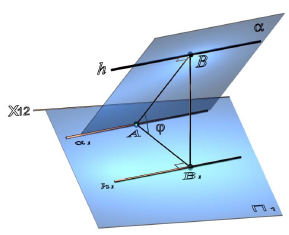
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:

Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой — обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.

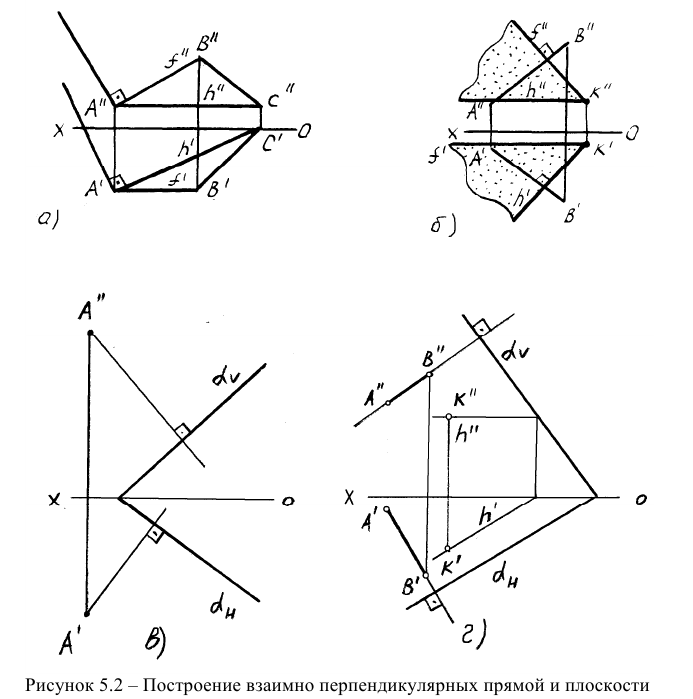
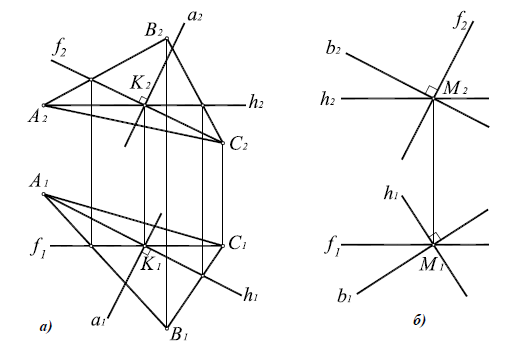
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.

Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) — через точку К проведена плоскость перпендикулярно прямой АВ.

Определение расстояний между геометрическими объектами

Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.

Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:

1. Из точки опустить перпендикуляр на заданную плоскость;
2. Найти точку встречи перпендикуляра с плоскостью;
3. Определить НВ расстояния между заданной и найденной точками.

Задача на определение расстояния от точки до прямой решается по следующему плану:

1. Через точку к провести плоскость, перпендикулярную заданной прямой;
2. Найти точку встречи М заданной прямой с проведенной плоскостью;
3. Соединить полученные точки (это будет перпендикуляр из точки на прямую);
4. Определить НВ перпендикуляра.

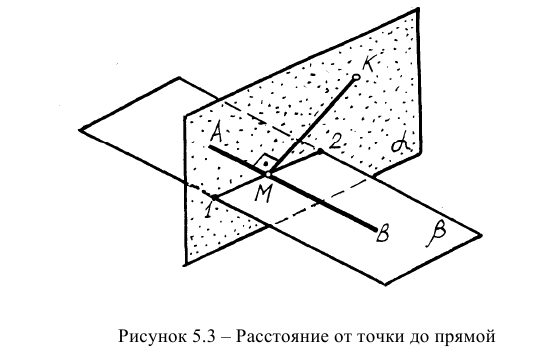
Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.

Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.

Перпендикулярность плоскостей

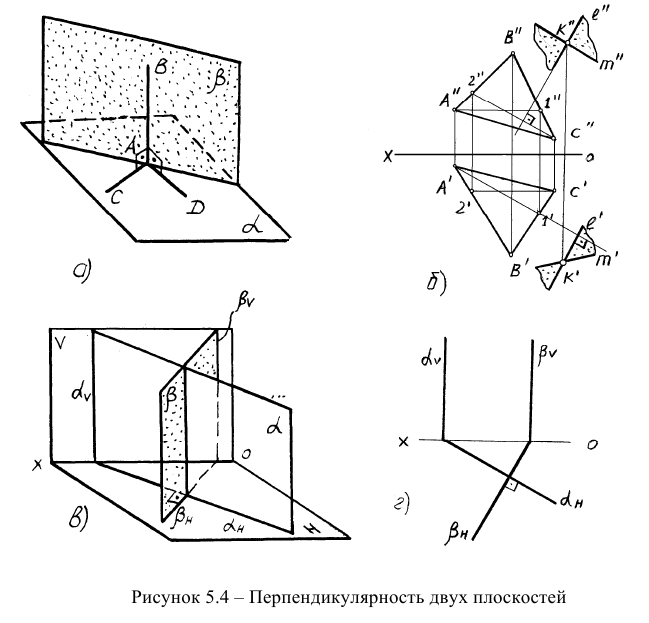
Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.

Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).

Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.

Определение углов между прямой и плоскостью и между двумя плоскостями

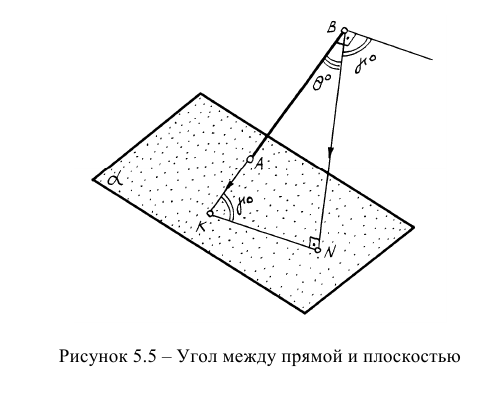
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:

1. Определить точку встречи прямой АВ с плоскостью а;
2. Из точки В построить перпендикуляр на плоскость;
3. Найти точку встречи перпендикуляра с плоскостью;
4. Точки К и N соединить и определить НВ угла BKN.

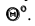
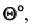
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла то искомый угол определится по формуле:

которую можно решить графически, достроив угол 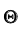до 90°.

То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.

С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 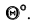Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:

Дополненный угол будет искомым.

Натуральную величину дополнительного угла в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.

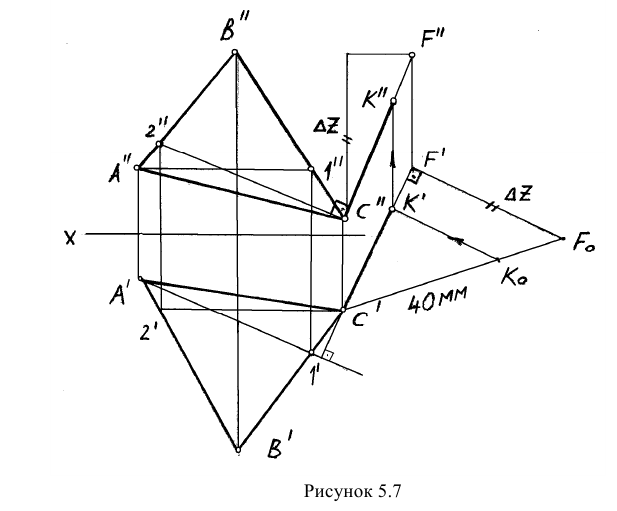
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.

Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).

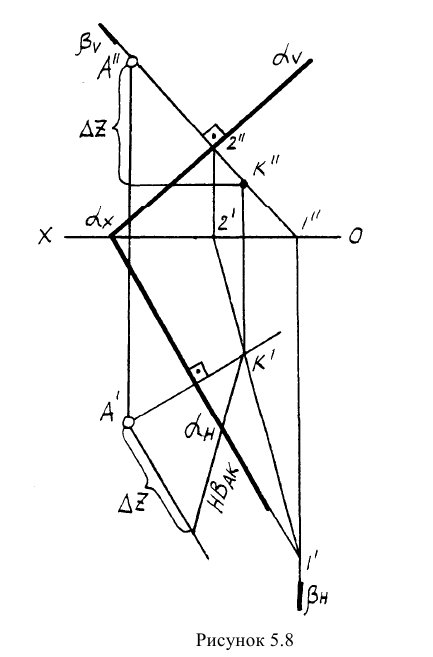
Пример: Найти расстояние от точки А до плоскости, заданной следами

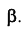
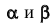
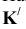
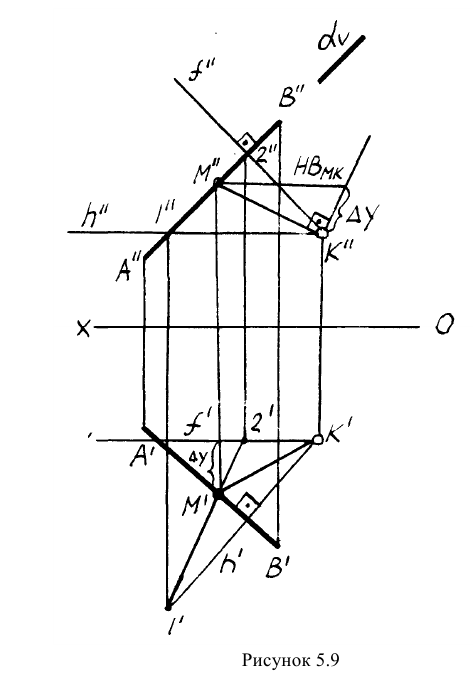
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости Находим линию пересечения плоскостей (линия 1-2) и точку встречи в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).

Пример: Определить расстояние от точки К до прямой AВ.

Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).

Видео:Расстояние от точки до плоскостиСкачать

Примеры метрических задач

Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.

Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.

Теорема о проекциях прямого угла

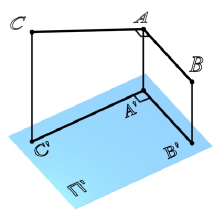
Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).

Рис. 10.1. Теорема о проекциях прямого угла

Дано :BAC = 90°; AB || П’

Доказать, что C’A’A’B’

Доказательство: если AB||П’, то A’B’||AB, но AA’П’^AA’A’B’ значит ABAA,AB плоскости CAA’C’, тогда и A’B’ CAA’C’. Следовательно,CA’A’B’.

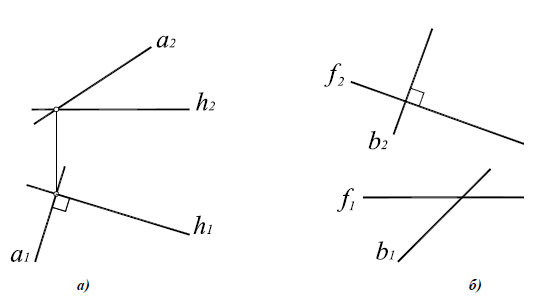
На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П₁ в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П₂ — если одна из них фронталь (рис. 10.2,а).

Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a₁ h₁ a h ;
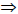
б -скрещивающиеся b2 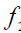₂ b

Линии наибольшего наклона плоскости

Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали — линией наибольшего наклона к фронтальной плоскости проекций.

Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).

Рис. 10.3. Линия наибольшего наклона плоскости а к П₁:
а — плоскость общего положения; h ∈α — горизонталь плоскости а; AB h — линия наибольшего наклона;
φ = AB, AB ₁ — угол наклона плоскости а к П₁

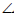
Перпендикулярность прямой и плоскости

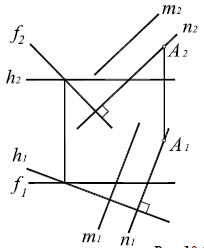
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция — фронтальной проекции фронтали плоскости.

Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня — горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция — фронтальной проекции фронтали плоскости.

Рис. 10.4. Перпендикулярность прямой и плоскости:

а -построение прямой, перпендикулярной плоскости:

б -построение плоскости, перпендикулярной прямой:

Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)

Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.

Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой

Взаимная перпендикулярность плоскостей

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(× h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α(×h): n₁h₁; n₂₂. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно — как пересекающая прямую n или параллельная ей.

Рис. 10.6. Перпендикулярность двух плоскостей

Дано: α(h × ) ; A (A₁, A₂).

Построить: A ∈ β α .

Видео:Замена плоскостей проекции(Расстояние от точки до прямой)Скачать

Определение метрических задач

Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.

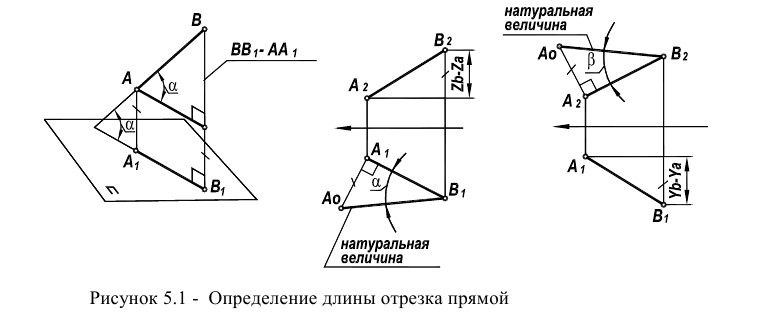
Определение длины отрезка

Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).

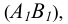
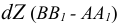
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции а второй катет -разница координат концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.

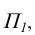
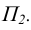
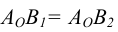
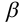
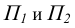
На комплексном чертеже возможно решение как на плоскости так и на плоскости При правильных построениях . Углы а и -углы наклона отрезка прямой АВ к плоскости соответственно.

Определение площади треугольника

Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.

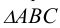
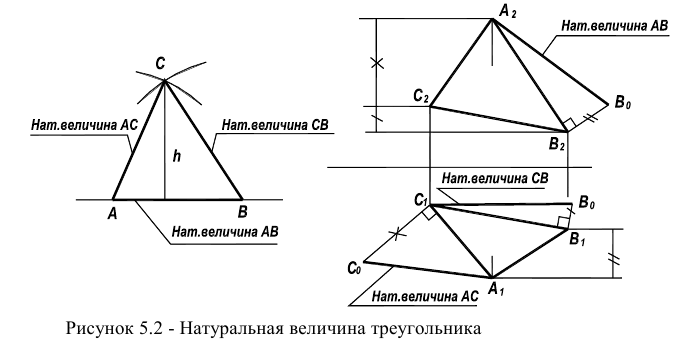
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон (в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.

Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.

Проецирование прямого угла

Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.

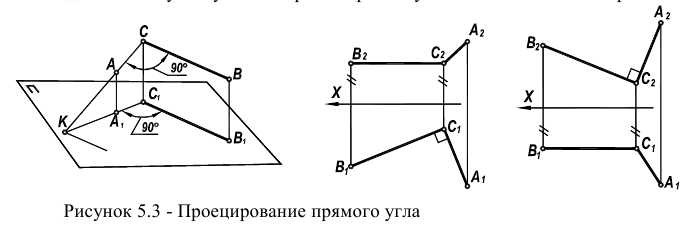
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на

соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая — ей не перпендикулярна.

Перпендикулярность прямых и плоскостей

Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.

Перпендикулярность прямой и плоскости

Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.

При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).

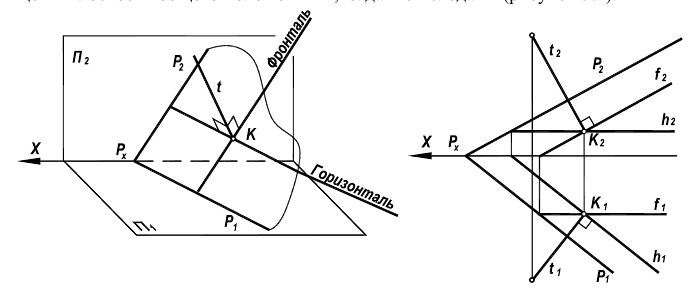
Рисунок 5.4 — Перпендикулярность прямой и плоскости

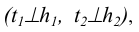
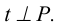
В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой .

В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).

Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:

а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости

Рисунок 5.5 — Перпендикуляр к плоскости

б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые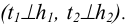— Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;

в) определяется точка S пересечения этого перпендикуляра t и плоскости.

Расстояние от точки до плоскости

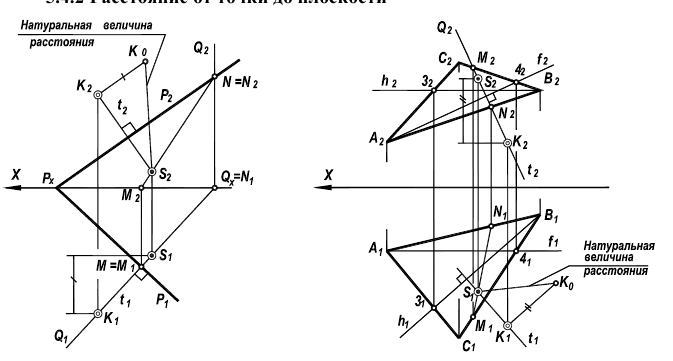
Рисунок 5.6 — Расстояние от точки до плоскости

Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)

Перпендикулярность плоскостей

Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.

При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).

Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).

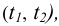
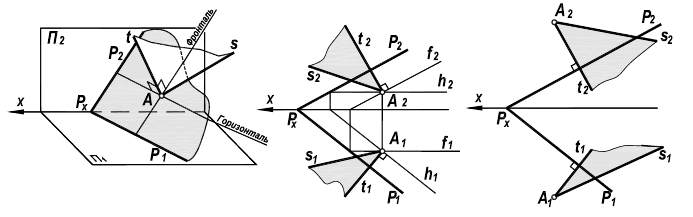
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.

Рисунок 5.7 — Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.

Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.

Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).

Рисунок 5.8 — Перпендикулярность плоскостей

Определение натуральных величин геометрических элементов

1. Определить натуральную величину отрезка общего положения:

• способом прямоугольного треугольника;
• способом замены плоскостей проекций преобразовать в прямую уровня;
• способом вращения вокруг проецирующей оси преобразовать в прямую уровня.

2. Определить натуральную величину плоскости общего положения (замкнутого отсека):

• способом замены плоскостей проекций преобразовать в плоскость уровня;
• способом вращения вокруг линии уровня преобразовать в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать в плоскость уровня.

Определение расстояния между геометрическими элементами (образами)

1. Определить расстояние от точки до прямой общего положения:

• способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
• способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.

2. Определить расстояние между параллельными прямыми:

• способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
• способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.

3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).

4. Определить расстояние от точки до плоскости:

• по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
• способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.

5. Определить расстояние от точки до поверхности вращения:

• способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
• способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.

Определение углов наклона геометрических элементов к плоскостям проекций H и V

1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:

• способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
• способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
• способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.

2. Определить угол наклона прямой к заданной плоскости общего положения:

• из любой точки прямой опустить перпендикуляр к плоскости;
• способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
• искомый угол будет дополнять построенный угол до 90°.

3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):

• способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).

4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):

• задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
• эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
• искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).

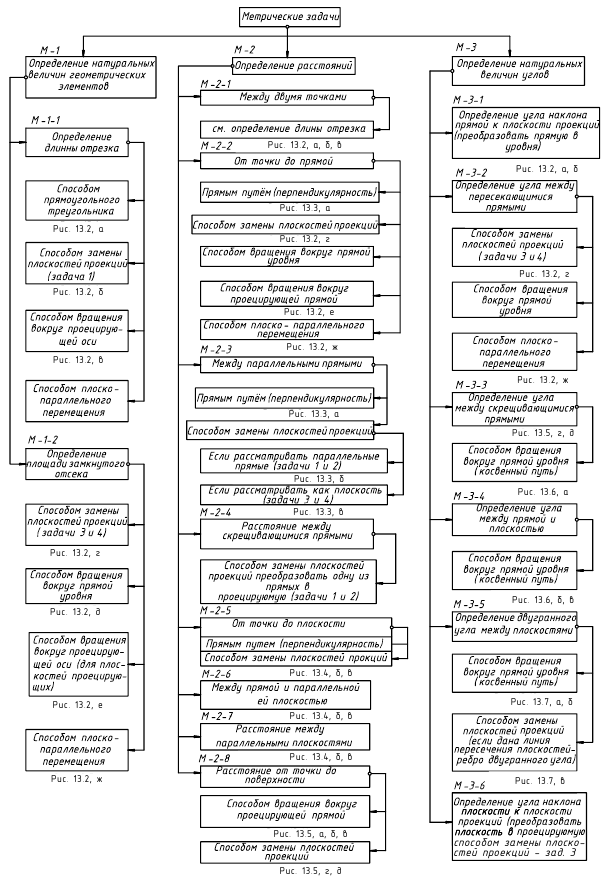
Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).

Метрические задачи:

Определение натуральной величины геометрических элементов:

1. Определение длины отрезка

Способ прямоугольного треугольника

Способ замены плоскостей проекций (задача 1)

Способ вращения вокруг проецирующей оси

2. Определение площади замкнутого отсека

Способ замены плоскостей проекций (задачи 3 и 4)

Способ вращения вокруг прямой уровня (горизонтали)

Способ вращения вокруг проецирующей оси i(i V)

Способ плоско-параллельного перемещения (переноса)

Определение расстояний:

1. Расстояние между точками — определяется величиной отрезка, соединяющего эти точки

2. Расстояние от точки до прямой — определяется величиной перпендикуляра, опущенного из точки к прямой

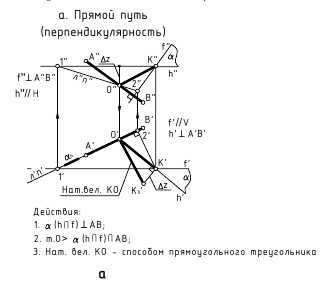
а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)

в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)

г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)

3. Расстояние между параллельными прямыми — определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой

а. Способ замены плоскостей проекции (рассматриваем две прямые) — задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)

б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) — задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))

4. Расстояние между скрещивающимися прямыми — определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).

Способ замены плоскостей проекций — задачи 1 и 2

5. Расстояние от точки до плоскости — определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.

а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую — задача 3)

6. Расстояние между прямой и параллельной ей плоскостью — определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.

7. Расстояние между параллельными плоскостями — определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).

8. Расстояние от точки до поверхности

a. Cпособ вращения вокруг проецирующей оси

б. Способ замены плоскостей проекции

Определение величин углов:

1. Угол φ между скрещивающимися прямыми — определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)

Способ вращения вокруг линии уровня

Дано:
а и b — скрещивающиеся прямые
Требуется:
∠φ — ?

Решение:
1.
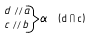
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)

2. Угол φ между прямой и плоскостью — определяется углом между прямой и её проекцией на эту плоскость.

Дано:
α(h ∩ f);
AB — прямая общего положения
Требуется:
∠φ — ?

Решение:
1. l α(h ∩ f);
l» f»;
l‘ h’;
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)

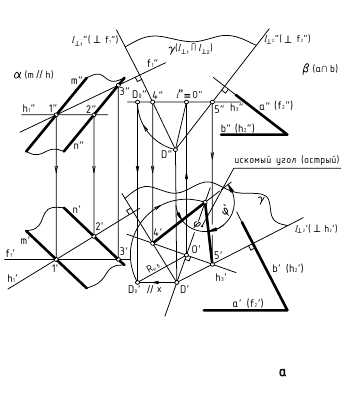
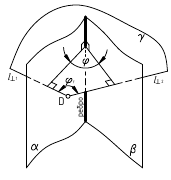
3. Угол φ между плоскостями α и β — определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).

а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) — угол φ определяется способом вращения вокруг линии уровня (рис. а)

Дано:
(m // h); (а ∩ b).
Требуется:
∠φ — ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;

2. из произвольной точки пространства D (D’, D») провести перпендикуляры l₁ и l₂ к заданными плоскостям, которые определяют плоскость γ(l₁ ∩ l₂);
3. ∠φ — вращением вокруг горизонтали h₃, проведённой в построенной плоскости γ(l₁ ∩ l₂).

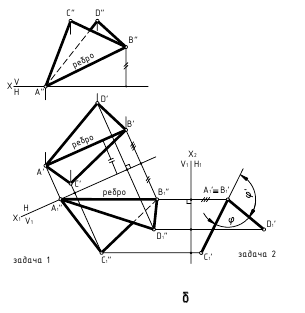
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) — угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)

ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.

• Тени в ортогональных проекциях
• Кривые поверхности
• Пересечения криволинейных поверхностей
• Пересечения поверхностей с прямой и плоскостью
• Пересечение поверхности плоскостью и прямой
• Развертки поверхностей
• Способы преобразования проекций
• Взаимное положение прямой и плоскости

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Метрические задачи

Содержание:

Метрическими называются задачи, решение которых связано с определением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Расстояние от точки до прямой и плоскости

Расстояние от точки до плоскости – это длина перпендикуляра, который опущен из заданной точки. Чтобы найти расстояние между скрещивающимися прямыми, необходимо воспользоваться знаниями о нахождении расстояния от точки до плоскости, поскольку для определения расстояния между скрещивающимися прямыми необходимо на одной из прямой выбрать точку.

Расстояние от точки до прямой особого положения

Метрические задачи по проецированию точки, прямой и плоскости связаны с определением расстояний, площадей, углов. Все задачи на определение расстояния от точки до прямой и плоскости, между параллельными прямой и плоскостью и двумя плоскостями сводятся к задаче об определении расстояния между двумя точками. Задачи по определению площади плоской фигуры сводятся к нахождению натуральной величины этой фигуры. Определение угла между двумя прямыми, прямой и плоскостью, двумя плоскостями невозможно без применения способов преображения комплексного чертежа (см. п. 2.1.6, 2.3.3). Методами, описанными в разделе 1, можно определить только проекции этих углов.

Для определения расстояния от точки А до прямой l необходимо провести из данной точки перпендикуляр n до прямой, определить точку N пересечения прямых n, l и найти длину отрезка AN. Последняя является искомым расстоянием (рис. 1.51).

Расстояние от точки до прямой общего положения

Определение расстояния от точки до прямой уровня

При определении расстояния от точки до прямой l особого положения прямой угол между прямыми l проецируется в натуральную величину на одну из плоскостей проекций (см. п. 1.4.8), а натуральная величина отрезка АN определяется способом прямоугольного треугольника (см. п. 1.4.4) или вращением вокруг проецирующей оси (см. п. 2.2.2).

На рис. 1.52 обозначено расстояние от точки А до горизонтали h. На горизонтальной проекции построена проекция А1N1 искомого отрезка. С помощью линий проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN определена способом прямоугольного треугольника.

Расстояние от точки до прямой общего положения

Задача на определение расстояния от точки А до прямой l общего положения усложняется тем, что проекции прямого угла между прямой l и проведённым к ней перпендикуляром не равны 90° (см. п. 1.4.8, рис. 1.25). Для решения этой задачи применяются такие способы:

а) способ вспомогательной нормальной плоскости (рис. 1.53);

б) способ замены плоскостей проекций (см. п. 2.1.3);

в) способ вращения вокруг проецирующей оси (см. п. 2.2.3).

Способ вспомогательной нормальной плоскости

Суть способа вспомогательной нормальной плоскости

Через точку А проводится плоскость Σ общего положения, перпендикулярная прямой l (рис. 1.53 б). Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке А. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой l. Основа N перпендикуляра находится как точка пересечения прямой l с перпендикулярной её плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф (см. п. 1.5.7). Натуральная величина отрезка AN равна искомому расстоянию от точки А до прямой l общего положения.

Расстояние от точки до плоскости особого положения

Для определения расстояния от точки А до плоскости Σ необходимо провести из данной точки перпендикуляр до плоскости, определить точку N их пересечения и найти длину отрезка AN.

При определении расстояния от точки А до плоскости особого положения прямой угол между прямой и одним из следов плоскости Σ проецируется в натуральную величину на соответствующую плоскость проекций (рис. 1.54).

На рис. 1.55 определено расстояние от точки А до горизонтально-проецирующей плоскости Σ. На горизонтальной плоскости проекций через точку А1 проведена проекция перпендикуляра до горизонтального следа плоскости с основой N1. При этом перпендикуляр — горизонтальная прямая уровня. С помощью линии проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN равна длине его горизонтальной проекции А1N1.

Расстояние от точки до плоскости особого положения

– Определение расстояния от точки до горизонтально-проецирующей плоскости

Расстояния от точки до плоскости общего положения

Задача на определение расстояния от точки D до плоскости Σ общего положения определяется таким способом. Из точки D проводится прямая , перпендикулярная плоскости Σ (см. п. 1.5.9, рис. 1.47 – 1.48), и определяется точка N их пересечения (см. п. 1.5.7, рис. 1.38). Натуральная величина отрезка DN равна расстоянию от точки D до заданной плоскости (рис. 1.56).

Расстояние от точки до плоскости общего положения

Определение расстояния от точки до плоскости

На рис. 1.57 плоскость Σ задана треугольником АВС. Для построения прямой , проходящей через точку D перпендикулярно до плоскости треугольника, в последнем проводятся горизонталь h и фронталь f. Горизонтальная проекция h1 горизонтали перпендикулярна горизонтальной проекции прямой, фронтальная проекция f2 фронтали перпендикулярна . Точка N пересечения прямой с плоскостью Σ определяется методом вспомогательной секущей плоскости. В данном случае прямая заключается во фронтально- проецирующую плоскость Ω, заданную фронтальным следом Ω2,и определяется линия k пересечения плоскостей Σ, Ω. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка АN определяется способом прямоугольного треугольника.

Расстояние между параллельными плоскостями, прямой и плоскостью. Расстояние между двумя прямыми

Расстояние между параллельными плоскостями Σ и Ω равно расстоянию от любой точки D одной плоскости до другой плоскости (рис. 1.58).

Расстояние между параллельными плоскостями

Определение расстояния между параллельными плоскостями

На рис. 1.59 одна из плоскостей Σ задана прямыми a, b, пересекающимися в точке D, другая Ω – горизонтальным и фронтальным следами . Из точки D опускается перпендикуляр на плоскость Ω. При этом горизонтальная проекция перпендикулярна горизонтальному следу плоскости, фронтальная проекция перпендикулярна фронтальному следу Точка N пересечения прямой с плоскостью Ω определяется методом вспомогательной секущей плоскости. в данном случае через прямую проводится горизонтально-проецирующая плоскость Ψ, заданная горизонтальным следом Ψ1, и определяется линия k пересечения плоскостей Ω, Ψ. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой l и плоскостью Σ (рис. 1.60) равно расстоянию от любой точки D прямой до плоскости.

На рис. 1.61 плоскость Σ задана горизонтальным и фронтальным следами . Из любой точки D, принадлежащей прямой l, опускается перпендикуляр на плоскость Σ и определяется точка N их пересечения с помощью горизонтально-проецирующей плоскости Ψ. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой и плоскостью

Определение расстояния между параллельными прямой и плоскостью

Расстояния между параллельными прямыми равно расстоянию DN от любой точки D одной прямой до другой прямой (рис. 1.62) и может быть определено способом вспомогательной нормальной плоскости (см. п. 1.6.1.2, рис. 1.53).

Расстояние между параллельными прямыми

Способ вспомогательной нормальной плоскости

На рис. 1.63 через точку D прямой l проводится Σ плоскость общего положения, перпендикулярная прямой Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке D. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой . Основа N перпендикуляра находится как точка пересечения прямой с перпендикулярной ей плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф. Натуральная величина отрезка DN равна искомому расстоянию между параллельными прямыми l, m.

Расстояние между скрещивающимися прямыми l, m равно наименьшему расстоянию от точек одной прямой до другой прямой (рис. 1.64) и определяется такими способами:

а) способом вспомогательной параллельной плоскости;

б) способами преобразования комплексного чертежа (см. п. 2.1.5, 2.2.5, 2.3.2).

Расстояние между скрещивающимися прямыми

Суть способа вспомогательной параллельной плоскости

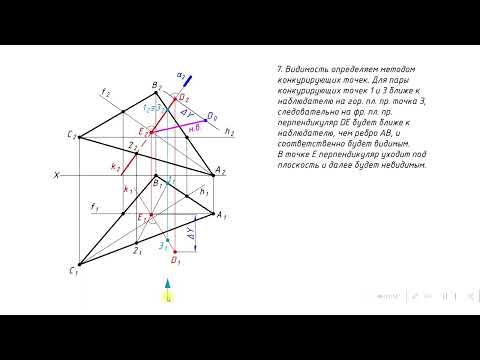
Расстояние между скрещивающимися прямыми равно расстоянию от любой точки D одной прямой до параллельной ей плоскости Σ, проведенной через вторую прямую (рис. 1.65).

Способ вспомогательной параллельной плоскости

На рис. 1.66 через прямую проведена плоскость Σ общего положения, заданная двумя прямыми пересекающимися в произвольной точке А. Эта плоскость параллельна прямой l, поскольку проекции прямой параллельны соответствующим проекциям прямой l. Для построения прямой , проходящей через точку D перпендикулярно плоскости Σ, в последней проводятся горизонталь h и фронталь f. Горизонтальная проекция прямой перпендикулярна горизонтальной проекции h1 горизонтали, фронтальная проекция перпендикулярна f2. Точка N пересечения прямой с плоскостью Σ определяется методом вспомогательной секущей плоскости . В данном случае, через прямую проводится горизонтально-проецирующая плоскость Ω, заданная горизонтальным следом Ω2, и определяется линия k пересечения плоскостей Σ, Ω.

Искомая точка N — точка пересечения прямых k, . Длина отрезка DN определяется способом прямоугольного треугольника.

Определение расстояния между скрещивающимися прямыми

Угол между прямой и плоскостью, двумя плоскостями

Угол φ между прямой l и плоскостью Σ определяется как угол между прямой l и её проекцией на эту плоскость (рис. 1.67 а).

Угол между прямой и плоскостью

На рис. 1.67 б плоскость Σ задана горизонтальным и фронтальным следами Проекция прямой l на эту плоскость проходит через отрезок , один конец которого (точка K) — точка пересечения прямой l с плоскостью Σ, другой (точка ) – точка пересечения прямой с плоскостью Σ. Прямая проходит через любую точку N прямой l перпендикулярно плоскости Σ. Горизонтальная проекция перпендикулярна следу , фронтальная проекция перпендикулярна до Ортогональными проекциями на плоскости проекций П1, П2 угла φ между прямой l и плоскостью Σ являются соответствующие проекции угла . Натуральная величина угла φ определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).

Угол θ между двумя плоскостями Σ, Ω называется двухгранным углом (рис. 1.68). Он определяется как угол между перпендикулярами к линии k пересечения плоскостей (прямая принадлежит плоскости Σ, прямая плоскости Ω).

Двухгранный угол

Вышеуказанные способы определения углов между прямой и плоскостью и двумя плоскостями относятся к прямым способам, базирующимся на использовании определения углов φ, θ. Прямые способы имеют существенный недостаток – громоздкость вспомогательных построений .

С целью упрощения практической реализации задачи построения углов φ, θ и чтения комплексного чертежа применяются непрямые способы, базирующиеся на свойствах этих углов

Свойство угла между прямой и плоскостью

Угол φ между прямой l и плоскостью Σ дополняет вспомогательный угол до 90° (рис. 1.69 а):

Вспомогательный угол -это угол между прямой l и перпендикуляром проведенным из любой её точки D к плоскости Σ.

Вспомогательный угол

На рис. 1.69 б плоскость Σ задана горизонтальным и фронтальным следами . Проекции прямоq n, проведенyной через произвольную точку D прямой l перпендикулярно плоскости Σ, перпендикулярны соответствующим следам этой плоскости. Натуральная величина угла определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).Угол φ определяется по формуле (1.1).

Свойство двухгранного угла

Угол θ между двумя плоскостями Σ, Ω равен углу между прямыми проходящими через произвольную точку пространства перпендикулярно этим плоскостям (рис. 1.70 а).

Непрямой способ определения двухгранного угла

На рис. 1.70 б плоскости Σ, Ω заданы горизонтальными и фронтальными следами и соответственно. Проекции вспомогательных прямых перпендикулярны соответствующим следам плоскостей Σ, Ω. Натуральная величина угла определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3). Угол θ между плоскостями Σ, Ω равен углу между прямыми .

Видео:Определение расстояния от точки до плоскости треугольникаНатуральная величина расстоянияСкачать

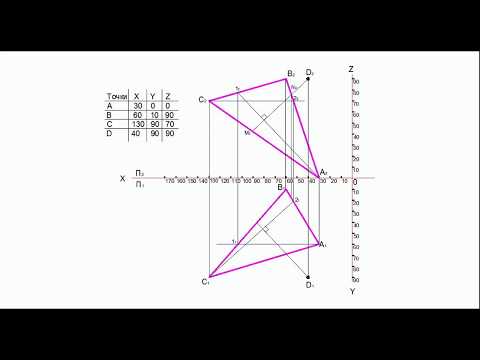
Метрические и позиционные задачи

Позиционными считаются задачи, решение которых позволяет полу-чить ответ о принадлежности точки или линии поверхности, а также зада—чи на определение общих элементов, принадлежащих различным геомет-рическим фигурам. Метрическими называются задачи, решение которых связано с нахо-ждением метрических характеристик геометрических фигур, определяе-мых линейными и угловыми величинами.

Длина дуги кривой линии

Задача на определение длины дуги s кривой линии является достаточно сложной. В начертательной геометрии она решается приближённо способом линейной интерполяции: дуга ОМ линии l разбивается на N участков которые условно заменяются одноимёнными отрезками прямых. Длина кривой ОМ определяется как сумма длин построенных отрезков с применением способов прямоугольного треугольника (рис. 3.74 а) или вращения вокруг проецирующих осей (рис. 3.74 б).

От количества N выбранных участков зависит точность определения длины дуги

Определение длины дуги кривой линии

Задача на определение длины кривой линии намного сложнее, чем расчёт площадей геометрических фигур и объёмов тел. В античные времена единственная удачная попытка определения длины кривой линии была предпринята для окружности.

Декарт высказывал ошибочную мысль, что «отношение между прямым и кривым неизвестно и не может быть познано человечеством»

. Первым достижением было определение длины дуги параболы Нейла в 1657 р. Позже К. Рэн и Х. Гюйгенс нашли длину дуги циклоиды. Незадолго до открытия математического анализа Дж. Грегори создал общую теорию нахождения дуги кривой линии.

Кристофер Рэн (Christopher Wren) – английский математик и архитектор, профессор математики в Оксфорде, член Королевского товарищества. Занимался вопросами кораблестроения, сопротивления жидкости, механикой вёсел и парусов и т.д.. Автор величественных архитектурных сооружений, в том числе Собора святого Павла.

Центр и радиус кривизны. Эволюта и эвольвента кривой

Кривизна любой линии l в точке М характеризуется двумя основными параметрами: центром и радиусом кривизны

Центр и радиус кривизны – центр С и радиус ρ окружности , которая является точнейшим приближением данной кривой l в окрестности её точки М (рис. 3.75 а).

Центр кривизны С находится на внутренней нормали кривой l в данной точке М. На рис. 3.75 б показан способ определения центра кривизны С плоской кривой l в точке М. В точке М и близко к ней расположенной точке N проведены касательные Центр кривизны С является точкой пересечения перпендикуляров к касательным. Радиус СМ построенной окружности с центром в точке С является радиусом ρ кривизны линии l в точке М..

Центр и радиус кривизны

Понятия центра и радиуса кривизны введены Лейбницем. Геометрическое место центров кривизны линии l для всех её точек называется эволютой (от латинского evolute – развитый). На рис. 3.76 показаны эволюты эллипса, дуги синусоиды и циклоиды. Для их построения на этих кривых выбирается совокупность точек … и проводятся касательные … и нормали , … Точки 1, 2, … пересечения последовательных пар нормалей являются точками, принадлежащими эволюте данной кривой. Например, эволюта эллипса (рис. 3.76 а) имеет форму звезды с двумя осями симметрии; эволюта половины дуги синусоиды (рис. 3.76 б) имеет две асимптоты и одну ось симметрии; эволюта ветви циклоиды (рис. 3.76 в) имеет одну ось симметрии.

Эволюты плоских кривых

Линия для которой заданная кривая l является эволютой, называется эвольвентой (от латинского evolvens – разворачивающий). Например, на рис. 3.76 а эллипс является эвольвентой фигуры в форме звезды.

Эволюты и эвольвенты широко используются в проектировании машин и механизмов. Например, зубчатые колёса (рис. 3.77) имеют профиль в форме кривой, эволюта которой является окружностью. Другими словами, такие зубчатые колеса имеют форму эвольвенты окружности.

Применение эвольвенты окружности

Для построения эвольвенты окружности (рис. 3.78) последняя делится на N равных частей (как правило, N = 12) точками , … Из этих точек проводятся отрезки …, касательные к окружности и с равномерно возрастающей длиной (от нуля до длины окружности). Эвольвента окружности проходит через точки 1, 2, …

Эвольвента окружности

Джеймс Грегори (James Gregory) – шотландский математик и астроном, член Королевского общества. Один из основателей математического анализа. Грегори является автором зеркального телескопа, метода определения расстояния от Земли до Солнца, способа числового интегрирования и разложения функций в бесконечные ряды.

Готфрид Вильгельм фон Лейбниц (Gottfried Wilhelm von Leibniz) – выдающийся немецкий философ, математик, физик, юрист, историк, дипломат, изобретатель, филолог; основатель и первый президент Берлинской академии наук, иностранный член Французской академии наук. Автор дифференциального и интегрального исчисления, учения про анализ и синтез, проектов научных исследований магнитного поля Земли. Лейбниц впервые ввёл термин «модель» в математических исследованиях и высказал мысль о возможности машинного моделирования функций человека. Лейбниц является автором механического арифмометра, прибора использования энергии ветра, чертежа подводной лодки, идеи создания паровой машины и т.д..

Эквидистанта кривой

Эквидистанта кривой (от латинского æquidistans – равноудалённый) – геометрическое место концов N отрезков одинаковой длины r, отложенных на нормалях к заданной кривой l (рис. 3.79 а).

На рис. 3.79 б построена эквидистанта кривой l. В точках … кривой l проводятся касательные … По одну сторону кривой l вдоль нормалей … откладываются отрезки, … одинаковой длины r, концы 1, 2, … которых принадлежат искомой эквидистанте.

Эквидистанта кривой

В металлообработке эквидистантой к траектории центра концевой фрезы является контур поверхности, которая получается в результате фрезерования. В системах автоматического раскроя плоских изделий (пластин, тканей и т.д.) эквидистанта является контуром, которым ограничивается припуск на обработку.

Расстояние от точки до кривой линии и поверхности

Расстояние от точки А до кривой линии — это наименьшее из всех расстояний l от этой точки до всех точек кривой

В начертательной геометрии расстояние l от точки А до кривой определяется способом конической поверхности (рис. 3.80).

Суть способа конической поверхности

Строится коническая поверхность Ф с направляющей , совпадающей с данной кривой, и вершиной А, которая совпадает с данной точкой. Среди совокупности прямолинейных образующих выбирается образующая l наименьшей длины.

На рис. 3.80 построен комплексный чертёж точки А и кривой . Строятся проекции образующих …, заданных отрезками , … Длины этих отрезков определяются способом вращения вокруг фронтально-проецирующей оси, проходящей через точку А. Натуральные величины … вращаются вокруг горизонтально-проецирующей оси, проходящей через точку А, до общего фронтального положения уровня.

Способ конической поверхности

Среди совокупности отрезков , … выбирается наименьший, длина которого равна искомому расстоянию от точки А до кривой .

Расстояние от точки А до кривой поверхности Ω является наименьшим из всех расстояний l от этой точки до всех точек поверхности Ω.

В начертательной геометрии расстояние l от точки А до кривой поверхности Ω определяется способом конических поверхностей.

Суть способа конических поверхностей.

Строятся конические поверхности … с вершиной А, которая совпадает с данной точкою, и направляющими , … совпадающими с направляющими поверхности Ω. Среди совокупности прямолинейных образующих каждой конической поверхности выбираются образующие … наименьших длин. По точкам полученных образующих …, принадлежащих поверхности Ω, строится кривая Расстояние от точки А до поверхности Ω равно расстоянию от этой точки до линии Она находится способом конической поверхности (рис. 3.80)

На рис. 3.81 построен комплексный чертёж точки А и поверхности Ω. Способом конических поверхностей (см. рис. 3.80) определяются наименьшие расстояния … от точки А до направляющих … По точкам 1, 2, … строятся проекции линии . Расстояние от точки А до кривой определяется способом конической поверхности (рис. 3.80)..

Описанные выше графические способы конических поверхностей являются приближенными и требуют громоздких построений. Точное, аналитическое определение расстояния от точки до кривой линии и поверхности является слишком сложной задачей поиска экстремума функции нескольких переменных параметров, которая может быть решена методами вариационного исчисления.

Способ конических поверхностей

Пересечение прямой линии с кривой поверхностью

Прямая линия l и кривая поверхность Ω могут иметь такие виды взаимного расположения:

а) прямая и поверхность не пересекаются (рис. 3.82 а);

б) прямая касается поверхности (см. п. 3.3, рис. 3.70 – 3.73);

в) прямая пересекает поверхность (рис. 3.82 б), в том числе перпендикулярна ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и кривой поверхности

Из п. 1.5.7 известно, что прямая пересекает поверхность первого порядка (плоскость) в одной точке. В случае поверхности второго и высших порядков прямая может пересекать поверхность в точках, количество которых не превышает порядок поверхности. Например, прямая может пересекать тор (поверхность четвертого порядка) максимум в четырёх точках (рис. 3.82 б).

Для определения точек пересечения прямой l с поверхностью Ω применяются такие способы:

а) способ вспомогательной секущей плоскости особого положения (см. п. 4.2.2.1, рис. 4.17 – 4.19);

б) способ вспомогательной секущей плоскости общего положения (см. п. 4.2.2.2, рис. 4.20 – 4.23);

в) способ замены плоскостей проекций (см. п. 4.2.2.3, рис. 4.24);

г) способ вращения вокруг проецирующей оси (см. п. 4.2.2.3, рис. 4.25 – 4.27);

д) метод последовательных приближений (см. п. 4.2.2.5);

е) способ косоугольного проецирования.

Все способы, кроме последнего, детально описаны в п. 4.1.2, 4.2.2 на примере гранных тел и поверхностей вращения.

Способ косоугольного проецирования является универсальным, то есть может быть использован для определения точек пересечения прямой l с любой кривой поверхностью.

На рис. 3.83 определена точка K пересечения прямой l с гиперболическим параболоидом Ω. Применён способ косоугольного проецирования на биссекторную плоскость Направление проецирования і совпадает с прямой l, поэтому проекция является точкой. Все точки и линии поверхности Ω также проецируются на биссекторную плоскость. Проекция точки пересечения прямой l с поверхностью Ω совпадает с проекцией Через точку проводится образующая принадлежащая поверхности . С помощью линии проекционной связи определяются проекция и проекции искомой точки K пересечения прямой l с гиперболическим параболоидом.

Определение точки пересечения прямой линии с кривой поверхностью

Пересечение кривой линии с плоскостью

Кривая линия l и плоскость Σ могут иметь такие виды взаимного расположения:

а) линия и плоскость не пересекаются (рис. 3.84 а);

б) плоскость касается лини (см. п. 3.3, рис. 3.70 – 3.73);

в) линия пересекает плоскость (рис. 3.84 б), в том числе перпендикулярна ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и плоскости

Кривая линия может пересекать плоскость в точках, количество которых не превышает порядок кривой. Например, эллипс (кривая второго порядка) пересекает плоскость максимум в двух точках (рис. 3.84 б).

Для определения точек пересечения линии l с плоскостью Σ применяются такие способы:

а) способ вспомогательной секущей цилиндрической поверхности (см. п. 4.2.2.4, рис. 4.29 – 4.30);

б) метод последовательных приближений (см. п. 4.2.2.5);

в) способ косоугольного проецирования.

Способ косоугольного проецирования может быть применён для определения точек пересечения плоскости Σ с любой кривой линией l.

На рис. 3.85 определены точки M, N пересечения кривой линииl с плоскостью Σ, заданной параллельными прямыми a, b, с применением способа косоугольного проецирования на биссекторную плоскость . Направление проецирования і совпадает с прямыми a, b, поэтому проекция является прямой. Все точки линии l также проецируются на биссекторную плоскость. Проекции точек пересечения линий l с плоскостью Σ принадлежат проекции . С помощью линий проекционной связи определяются горизонтальная и фронтальная проекции искомых точек M, N..

Определение точек пересечения кривой линии с плоскостью

Задачи на пересечение кривой линии с поверхностью, а также на пересечение поверхности плоскостью или другой поверхностью детально рассмотрены в разделе 4.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🔥 Видео

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

расстояние от точки до плоскостиСкачать

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Расстояние от точки до плоскостиСкачать

Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Расстояние от точки до прямойСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

[Начертательная геометрия] Расстояние от точки до плоскости, перпендикуляр к плоскости 1 частьСкачать

Точка встречи прямой с плоскостьюСкачать

18. Расстояние от точки до прямой в пространствеСкачать