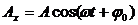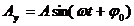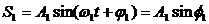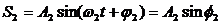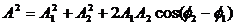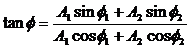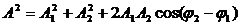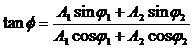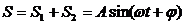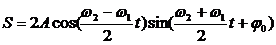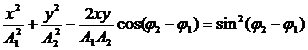Вектор амплитуды сложение гармонических колебаний

Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Метод векторных диаграмм

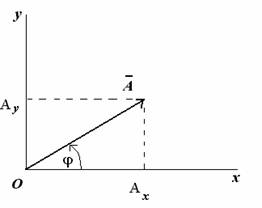
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j₀ где j₀ — начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 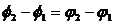, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

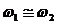
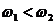
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

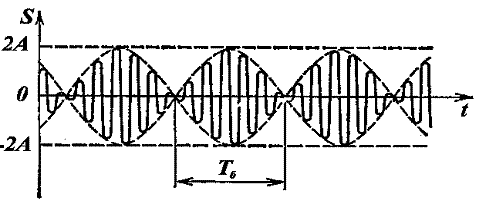
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 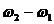— частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это — уравнение эллипса. При A₁=A₂ — окружность, при 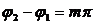(m — целое) — отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Видео:Урок 337. Сложение колебаний одной частоты. Метод векторных диаграммСкачать

Вращающийся вектор амплитуды

4.2. Вращающийся вектор амплитуды

Если одна и та же материальная точка участвует в нескольких колебательных процессах одновременно, то ее смещение в любой момент времени можно найти геометрически методом вращающегося вектора амплитуды (методом векторных диаграмм).

Изобразим на координатной плоскости XOY вектор А с началом в точке О (рис. 24).

Рис. 24. Проекции вектора А на координатные оси совершают гармонические колебания с частотой О)

Длина вектора А равна амплитуде колебаний. Угол, образуемый вектором А с осью ОХ, равен начальной фазе колебания ф₀. Если привести вектор А во вращение вокруг начала координат О с частотой, равной циклической частоте колебания (о, то его проекции на координатные оси ОХ и OY будут изменяться по гармоническому закону:

Рассмотрим некоторые частные случаи сложения гармонических колебаний методом векторных диаграмм.

Видео:67. Сложение колебанийСкачать

Сложение гармонических колебаний одного направления

Пусть два гармонических колебания происходят в одном направлении ОХ, имеют одинаковые частоты C0j = (о₂ = со, но различные начальные фазы ф, ф ф₂. Запишем уравнения этих колебаний:

Результирующее смещение точки равно:

Амплитуду и начальную фазу (А,ф) результирующего колебания найдем методом векторных диаграмм (методом вращающегося вектора амплитуды). Изобразим на координатной плоскости два вращающихся вектора амплитуд А, и А, (рис. 25).

Рис. 25. Сложение гармонических колебаний одного направления и одинаковой частоты графическим методом

Углы, образуемые этими векторами с осью ОХ в начальный момент времени ф₁ иф., равны начальным фазам колебаний. Так как вектора

А, и А, вращаются вокруг начала координат с одинаковой угловой скоростью со, равной круговой частоте колебаний, то угол между ними не меняется со временем и равен ср = ф] — (р₂ •

Как следует из рис. 3, амплитуда результирующего колебания (длина вектора А) равна

а начальная фаза определяется соотношением:

Если разность фаз колебаний равна четному числу полуоборотов, или другими словами четному числу ж радиан, то есть:

то амплитуда результирующего колебания будет максимальной:

Если разность фаз колебаний равна нечетному числу полуоборотов, или другими словами нечетному числу ж радиан, то есть:

то амплитуда результирующего колебания будет минимальной:

Видео:Урок 327. Гармонические колебанияСкачать

Сложение гармонических колебаний

Вы будете перенаправлены на Автор24

Сложением колебаний называют применение закона, описывающего состояние колебательной системы, если она принимает участие одномоментно в нескольких колебательных процессах.

При этом выделяют два предельных случая:

1. суммирование колебаний, имеющих одинаковые направления;
2. сложение взаимно нормальных колебаний.

К первому варианту сложения колебаний можно отнести случай, когда груз ($a$) совершает колебания на пружине 1 относительно другого колеблющегося груза ($b$) и совместно с ним на пружине 2 (рис.1).

Рисунок 1. Суммирование колебаний, имеющих одинаковые направления. Автор24 — интернет-биржа студенческих работ

Такой случай реализуется при наложении колебаний скалярных физических параметров, характеризующих систему колебаний, например:

• давления;
• температуры;
• плотности;
• силы тока;
• заряда и т.д.

Видео:Урок 336. Векторное представление колебанийСкачать

Суммирование однонаправленных гармонических колебаний

Сложение пары гармонических колебаний вида:

$s_1=A_1 sin (omega_1 t+varphi_1) (1)$ и $ s_2=A_2 sin (omega_2 t+varphi_2) (2)$

можно выполнить, если воспользоваться методом векторных диаграмм.

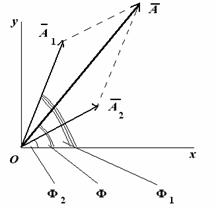
Рисунок 2. Метод векторных диаграмм. Автор24 — интернет-биржа студенческих работ

Рисунок 2 показывает векторы $vec A_1(t)$ и $vec A_2(t)$ амплитуд соответствующих колебаний в момент времени $t$. Фазы этих колебаний в обозначенный момент времени равны:

$Ф_1=omega_1 t+varphi_1 (3)$ и $Ф_2=omega_2 t+varphi_2 (4)$.

Готовые работы на аналогичную тему

Суммарному колебанию $s=s_1+s_2$ соответствует вектор:

проекция вектора $s$ на ось $Y$ равна:

Используя теорему косинусов, получим:

Видео:Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать

Когерентные и некогерентные гармонические колебания

Пару колебательных процесса называют когерентными в том случае, если их течение согласовано во времени, при этом разность их фаз не изменяется:

Из выражения (8) следует, что гармонические колебания будут когерентными, если

их круговые частоты будут одинаковыми:

в каждый момент времени разность фаз когерентных колебаний равна разности фаз их начальных колебаний:

Сложение двух гармонических однонаправленных когерентных колебаний дают колебание с той же круговой частотой $omega$, что исходные колебания, при этом имеем:

где $A^2=A_1^2+A_2^2+2A_1A_2cos (varphi_2-varphi_1)$;

Амплитуда суммарных колебаний изменяется в зависимости от разности начальных фаз:

от $A=|A_1-A_2|$ при $varphi_2-varphi_1=pm (2n+1)pi$

до $A=A_1+A_2$ при $varphi_2-varphi_1=pm 2npi$,

где $n=0,1,2. $ — целое положительное число или ноль.

При $varphi_2-varphi_1=pm 2npi$ колебания происходят в одной фазе (колебания называют софазными).

Если $varphi_2-varphi_1=pm (2n+1)pi$ колебания происходя в противофазе.

Если складываются гармонические колебания с разными циклическими частотами (некогерентные колебания), получаются негармонические колебания. Векторы амплитуд $A_1$ и $A_2$ вращаются с разными угловыми скоростями, построенный на них параллелограмм постоянно искажается, его диагональ изменяет длину и совершает вращения с изменяющейся угловой скоростью.

Пару гармонических колебаний, имеющих разные круговые частоты можно приближенно считать когерентными только на малом отрезке времени, в течение которого разность фаз колебаний изменяется на малую величину.

Сумму двух гармонических колебаний с разными, но близкими по величине круговыми частотами называют биениями.

Биения – это негармоническое колебание.

Видео:Урок 338. Сложение колебаний близких частот. БиенияСкачать

Суммирование взаимно перпендикулярных гармонических колебаний

Точка $N$ совершает одновременно два колебания. Они имеют одинаковые круговые частоты. Одно из них происходит вдоль оси $X$, другое вдоль оси $Y$. Их законы запишем как:

$x=A_1sin (omega t+varphi_1) (10)$ и

$y=A_2sin (omega t+varphi_2) (11),$

где $x$ и $y$ — декартовы координаты точки N.

Уравнение траектории движения точки N при этом:

Траектория движения точки имеет форму эллипса. Точка $M$ описывает данный эллипс за период суммируемых колебаний. Такие движения точки называют эллиптически поляризованными колебаниями.

Ориентация этого эллипса в плоскости $XOY$ и его размеры зависят от амплитуд складываемых колебаний $A_1$ и $A_2$ и разности начальных фаз $varphi_2-varphi_1$.

При $varphi_2-varphi_1=(2n+1)frac$, где $n=0,pm 1, pm 2. $ оси эллипса будут совпадать с осями $OX$ и $OY$, при этом величины его полуосей равны $A_1$ и $A_2$:

Если помимо прочего, $A_1=A_2$, то траекторией точки $N$ является окружность. При этом движение точки $N$ называют поляризованными циркулярно колебаниями (колебаниями которые поляризованы по кругу).

При $varphi_2-varphi_1=npi$ где $n=0,pm 1, pm 2. $, эллипс вырожден в отрезок прямой, при этом:

где знак плюс в выражении (14) при четных значениях $n$, то есть если складываются синфазные колебания; минус ставят при нечетных значения $n$, то есть если складываются колебания в противофазе. Такие колебания точки $N$ называют линейно поляризованными.

При линейно поляризованных колебаниях точка $N$ совершает гармонические колебания с частотой суммируемых колебаний и амплитудой, равной:

вдоль прямой линии, которая составляет с осью $OX$ угол:

Пусть взаимно нормальные колебания, имеющие циклические частоты $pomega$ и $qomega$, где $p$ и $q$ — целые числа:

$x=A_1sin (pomega t+varphi_1)$ и $y=A_2sin (qomega t+varphi_2) (16).$

Координаты $x$ и $y$ точки $N$, которая совершает колебания, одновременно повторяется спустя одинаковые отрезки времени $T_0$, равные общему минимальному кратному:

$T_1=frac$ и $T_2=frac$ периодов вдоль осей $OX$ и $OY$. Следовательно, траекторией точки $N$ является замкнутая кривая. Форма этой кривой связана с соотношением между:

• амплитудами,
• частотами,
• начальными фазами

суммируемых колебаний. Эти траектории точки $N$, выполняющей гармонические колебания в двух взаимно нормальных плоскостях одновременно, называют фигурами Лиссажу.

Фигуры Лиссажу можно вписать в прямоугольник:

• с центром, совпадающим с началом координат;
• сторонами параллельными осям координат ($OX$ и $OY$) и находящимися по обе стороны от них на расстояниях равных $A_1$ $A_2$;
• отношение частот суммируемых колебаний определяет количество касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси $OY$ и со стороной, параллельной оси $OX$.

🔍 Видео

Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Выполнялка 53.Гармонические колебания.Скачать

Величины, характеризующие колебательное движение | Физика 9 класс #24 | ИнфоурокСкачать

Сложение N колебаний методом векторных диаграммСкачать

Гармонические колебания Сложение гармонич колебаний Биения Фигуры ЛиссажуСкачать

Урок 340. Сложение колебаний кратных частот. Гармонический анализ и синтезСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Фигуры ЛиссажуСкачать