Точки М и N — середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О — точка пересечения медиан грани АВС.
а) Докажите, что прямая DO проходит через середину отрезка MN.
б) Найдите угол между прямыми MN и ВС, если АВСD — правильный тетраэдр.
а) Пусть О — точка пересечения медиан треугольника АВС; М — середина АВ, N — середина CD. Прямые DO и MN лежат в плоскости DMC и пересекаются в точке K.
Покажем, что K — середина MN.
Проведём в плоскости DMC.
Тогда — как средняя линия точка Н — середина ОС.
По свойству медиан треугольника, Пусть , тогда ; , т.к. H — середина OC.
Треугольники МКО и МNH подобны по двум углам, , и это значит, что
б) Пусть ABCD — правильный тетраэдр, все его ребра равны. Найдем угол между прямыми MN и BC,
Пусть F — середина AC;
MF — средняя линия треугольника АВС, Угол между прямыми MN и BC равен углу между MN и MF.
— равнобедренный, т.к. ABCD — правильный тетраэдр, MF=FN.
Легко доказать, что скрещивающиеся ребра правильного тетраэдра попарно перпендикулярны, то есть Действительно, если Е — середина ВС, то АЕ — медиана и высота правильного треугольника АВС, Прямая АЕ — проекция прямой AD на плоскость основания, и по теореме о трех перпендикулярах
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Р.К.Гордин, Ященко И.В ЕГЭ задание 14 математика 11 класс профильный
ПОДЕЛИТЬСЯ
Р. К. Гордин ЕГЭ 2020 математика 11 класс геометрия, стереометрия задача 14 (профильный уровень) под редакцией И. В. Ященко соответствует ФГОС.
Ссылка для скачивания пособия задание №14 ЕГЭ: скачать сборник
Р.К.Гордин, Ященко И.В ЕГЭ задание 14 математика 11 класс профильный уровень ФГОС:
Некоторые задания:
1)Дан параллелепипед ABCDA1B1C1D1. Постройте прямую пересечения плоскостей BB1D1 и АВС1.
2)Основание пирамиды SABCDEF — шестиугольник ABCDEF, противоположные стороны которого попарно равны и параллельны. Постройте прямую пересечения плоскостей ASD и CSF.
3)Дана шестиугольная призма ABCDEFA1B1C1D1E1F1, основания которой — правильные шестиугольники. Точка О —центр основания ABCDEF, М— середина бокового ребра DDV Постройте прямую пересечения плоскости А1В1С1 с плоскостью, проходящей через точки О и М параллельно прямой АЕ.
4)Дана четырёхугольная пирамида SABCD, основание которой — параллелограмм ABCD. Точка М лежит на боковом ребре SC. Постройте точку пересечения прямой ВМ с плоскостью ASD.
5)Точки М и N — середины рёбер соответственно АС и треугольной призмы АВСА1В1С1. а) Постройте прямую пересечения плоскостей MNC1 и А1С1 б) В каком отношении плоскость MNC, делит ребро АВ?
6)Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точки М и N — середины рёбер SA и SC соответственно. а) Постройте сечение пирамиды плоскостью, проходящей через точки М, N и В. б) В каком отношении плоскость сечения делит отрезок, соединяющий вершину S с центром основания пирамиды?
7)Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точка М — середина ребра ВС. а) Постройте прямую пересечения плоскостей FSM и ASB. б) В каком отношении плоскость FSM делит отрезок, соединяющий точку А с серединой ребра SD?
8)Основание пирамиды SABCD—параллелограмм ABCD. Точка К лежит на ребре SD и отлична от S и D. а) Может ли сечение пирамиды плоскостью, проходящей через прямую АВ и точку К, быть параллелограммом? б) Пусть К — середина ребра SD, М — середина ребра АВ, а пирамида SABCD правильная, причём все её рёбра равны. Найдите угол между прямыми АК и SM.
9)Дана четырёхугольная пирамида SABCD, основание которой — прямоугольник ABCD, а высота проходит через центр О основания. Через середину А1 бокового ребра SA проведена плоскость а, параллельная плоскости основания, а через середину С1 бокового ребра SC и ребро АВ — плоскость b. Найдите угол между плоскостями а и 13, если АВ : ВС: SA = 8: 6:13.
10)Дана правильная четырёхугольная пирамида SABCD с вершиной S. Все рёбра пирамиды равны, Е —середина бокового ребра SC. Найдите углы между плоскостями: a) SAD и SBC; б) АВС и SCD; в) АВС и BDE; г) BSC и DSC; д) АВЕ и АВС.
11)Дана правильная шестиугольная пирамида SABCDEF с вершиной S. Стороны основания равны 1, боковые рёбра равны 2. Точка G — середина ребра SC. Найдите расстояния: а) от точки S до прямой BF; б) от точки В до прямой SA; в) от точки F до прямой BG; г) от точки А до прямой SD; д) от точки А до прямой SC; е) от точки А до плоскости SDE; ж) от точки А до плоскости SBF; з) от точки А до плоскости SCE.
12)Высота PC треугольной пирамиды РАВС с вершиной Р проходит через точку С. Прямые РА и ВС перпендикулярны. а) Докажите, что основание пирамиды — прямоугольный треугольник. б) Найдите углы, которые образуют боковые рёбра РА и РВ с плоскостью основания, если АС = 6, ВС — 8, а расстояние от точки Р до прямой АВ равно 5.
13)Точка М — середина ребра АВ правильного тетраэдра DABC. а) Докажите, что ортогональная проекция точки М на плоскость ACD лежит на медиане АР грани ACD. б) Найдите угол между прямой DM и плоскостью ACD.
14)Дана правильная четырёхугольная пирамида РАВCD с вершиной в точке Р. Через точку С и середину ребра АВ перпендикулярно к основанию пирамиды проведена плоскость а. а) Докажите, что плоскость а делит ребро ВР в отношении 2: 1, считая от точки В. б) Найдите площадь сечения пирамиды плоскостью а, если известно, что РА = 10, АС = 16.
15)Через середину ребра АВ куба ABCDA1B1C1D1 проведена плоскость, параллельная прямым BD1 и А1С1. Докажите, что эта плоскость делит диагональ DB1 в отношении 3 : 5, считая от от вершины D.
16)Высота конуса равна 6, а радиус основания равен 8. а) Докажите, что наибольшая площадь сечения конуса плоскостью, проходящей через его вершину, равна 50. б) Найдите расстояние от центра основания конуса до этой плоскости.
17)В окружность основания конуса с вершиной Р вписан правильный шестиугольник ABCDEF. а) Докажите, что объём пирамиды PABD вдвое больше объёма пирамиды PDEF. б) Найдите площадь сечения конуса плоскостью АВР, если радиус основания конуса равен 6, а длина его образующей равна 9.
18)На ребре SD правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM: MD = 1:4. Точки Р и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
19)В правильной треугольной пирамиде SABC сторона АВ основания АВС равна 12, а боковое ребро SA равно 8. Точки М и N — середины рёбер SA и SB соответственно. Плоскость а проходит через прямую MN и перпендикулярна плоскости основания пирамиды.
Видео:Ященко. ЕГЭ. Профильная математика. 1 вариант. 2023. 13 задание. GeoGebra.Скачать
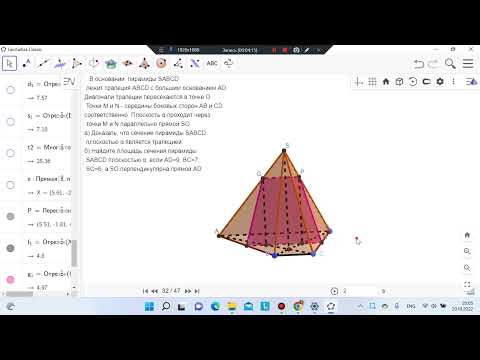
Основание пирамиды sabcd четырехугольник abcd точки m n и k середины
Вопрос по геометрии:
В основании пирамиды SABCD (SA=SB=SC=SD=b)лежит квадрат ABCD со стороной a. Точки K, L, M, N — середины ребер AD, SA, SB, BC соответственно. Найдите периметр четырехугольника KLMN.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
KN соединяет середины сторон основания и равна CD=а.
МL соединяет середины боковых ребер и равна АВ:2= а/2.
KL=MN соединяют середины сторон основания и боковых ребер, являются средними линиями ∆ SBC и ∆ SAD и равны b/2 ⇒
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
📹 Видео
Как строить сечения тетраэдра и пирамидыСкачать

Построение сечения пирамиды по трем точкамСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Геометрия Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекаетсяСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Как строить сечения параллелепипедаСкачать

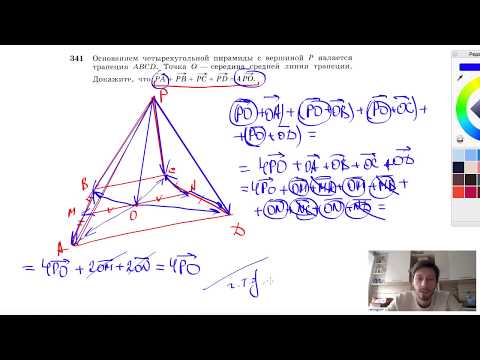
№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать
ЕГЭ 2023 стереометрия 1 вариантСкачать

Задача по стереометрии С2. ЕГЭ. Профильный уровень.Скачать

№3. Как строить сечения пирамидСкачать

Задание 14 (из 278 варианта Ларина)Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

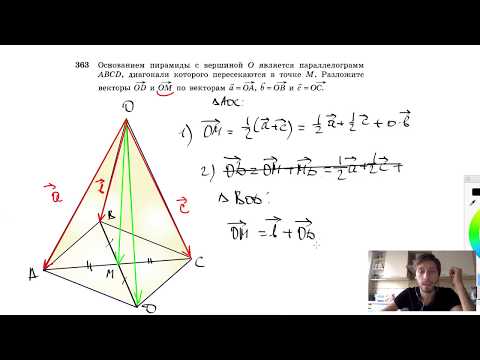
№363. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которогоСкачать
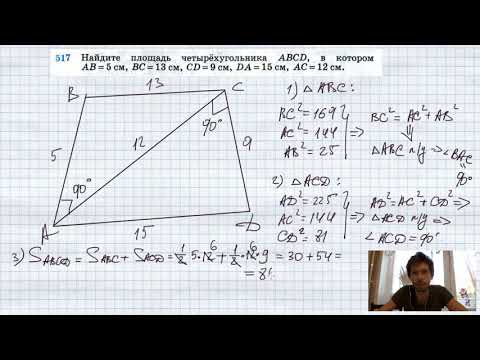
№517. Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 смСкачать
Урок 2. Как найти угол между прямыми || Задание №13. Стереометрия на ЕГЭСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать


